交流伺服系統(tǒng)的高響應(yīng)電流環(huán)控制

趙云， 廖政斌， 王澤飛， 蔡美東

(湖北工業(yè)大學(xué) 太陽能高效利用及儲(chǔ)能運(yùn)行控制湖北省重點(diǎn)實(shí)驗(yàn)室， 湖北 武漢 430070)

通過控制永磁同步電機(jī)(PMSM)，交流伺服系統(tǒng)可實(shí)現(xiàn)高效率、高精度、高響應(yīng)性能的目標(biāo)[1-2].常用的控制方式有比例-積分(PI)控制和滯環(huán)控制.PI控制雖然簡單、方便，但交軸(q軸)與直軸(d軸)存在耦合，影響電流環(huán)動(dòng)態(tài)響應(yīng)[3]；滯環(huán)控制的電流環(huán)響應(yīng)雖快，但該算法下的開關(guān)頻率不固定，輸出的電流含有諧波畸變，且存在穩(wěn)態(tài)誤差[4-5].因此，為了提高伺服系統(tǒng)電流環(huán)響應(yīng)性能，保證電流穩(wěn)定輸出，可通過速度指令前饋和加速度指令前饋提高系統(tǒng)響應(yīng)，并通過三次諧波的注入降低調(diào)制波的幅值，提高直流電流的利用率.文獻(xiàn)[6-7]在一個(gè)載波周期內(nèi)對定子電流進(jìn)行雙采樣和雙脈沖寬度調(diào)制(PWM)刷新，以減少采樣延時(shí)，提高系統(tǒng)的響應(yīng)性能.然而，以上方法在提高電流環(huán)帶寬方面都較為單一.基于此，本文針對不同的延時(shí)采取不同解決方法，提出一種復(fù)矢量解耦的電流環(huán)預(yù)測控制算法.

1 交流伺服系統(tǒng)電流環(huán)PI控制性能分析

1.1 電流環(huán)模型

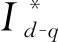
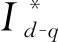
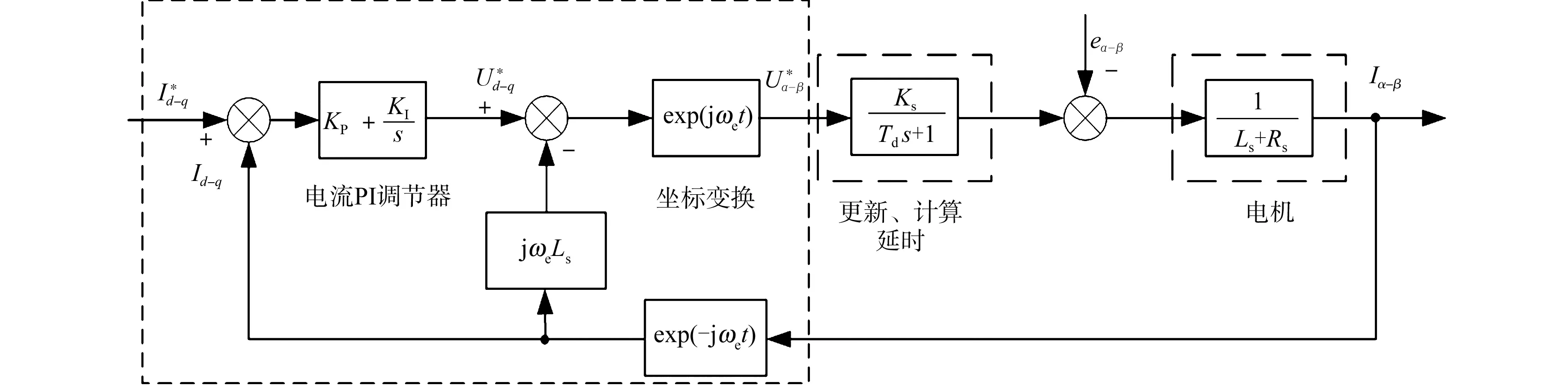
圖1 電流環(huán)PI控制算法的結(jié)構(gòu)框圖Fig.1 Structural block diagram of current loop PI control algorithm

在同步旋轉(zhuǎn)坐標(biāo)系下，可得q軸電壓Uq為

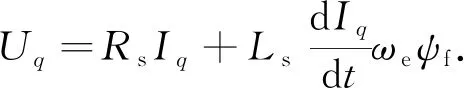
(1)

式(1)中：Iq為q軸電流；ψf為永磁體磁鏈.

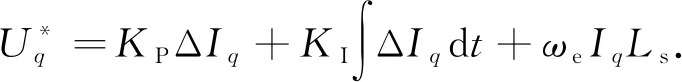
(2)

式(2)中：ΔIq為q軸電流的變化量.

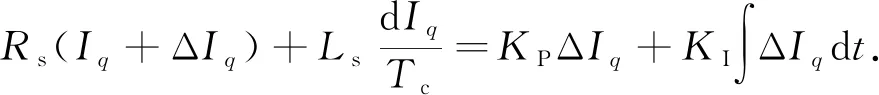
(3)

式(3)中：Tc為一個(gè)控制周期.

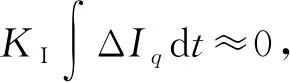
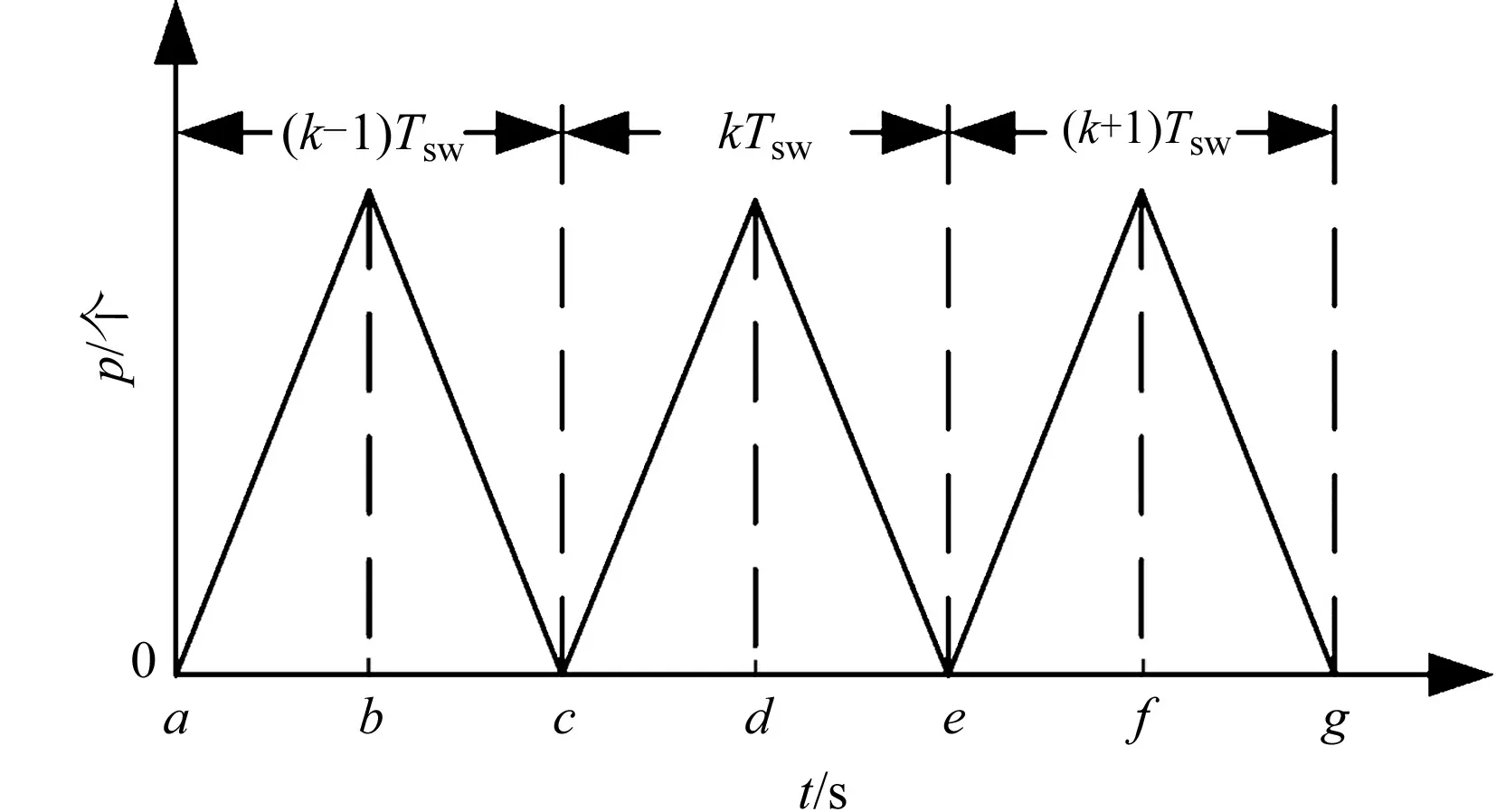
圖2 電流采樣時(shí)序示意圖Fig.2 Schematic diagram of current sampling sequence

由式(4)可知：電流環(huán)帶寬和控制周期成反比.一個(gè)控制周期Tc存在采樣延時(shí)、控制算法計(jì)算延時(shí)和PWM輸出延時(shí)等情況，從而影響電流環(huán)響應(yīng)性能.電流采樣時(shí)序示意圖[8]，如圖2所示.圖2中：p為脈沖個(gè)數(shù)；a～g為采樣時(shí)刻；k為周期個(gè)數(shù)；Tsw為逆變器開關(guān)周期.

1.2 電流環(huán)延時(shí)分析

在PI控制算法的電流采樣中，Tc=Tsw.占空比在脈沖數(shù)遞減為0時(shí)刻進(jìn)行更新；在a時(shí)刻，系統(tǒng)對電流進(jìn)行采樣，得到采樣電流，通過電流環(huán)預(yù)測控制算法計(jì)算逆變器輸出占空比，再執(zhí)行其他控制任務(wù)；在c時(shí)刻，系統(tǒng)將占空比更新到PWM發(fā)生器的比較單元，并在該開關(guān)周期內(nèi)保持不變；在e時(shí)刻，逆變器產(chǎn)生輸出電壓.由此可知，典型電流采樣時(shí)序的電流環(huán)延時(shí)Td=2Tc.

為改善輸出電壓滯后的問題，采用占空比雙次刷新電流采樣，占空比在脈沖數(shù)遞增到峰值時(shí)刻和遞減到0時(shí)刻進(jìn)行更新，電流環(huán)的控制周期縮減一半，即Tc=0.5Tsw，電流環(huán)延時(shí)變?yōu)門d=Tc，但控制周期的減小會(huì)加重運(yùn)算負(fù)荷，因此，對控制器運(yùn)算性能要求較高.

占空比雙次刷新PI控制算法雖然可解決電壓輸出滯后的問題，但電流采樣仍存在延時(shí).在占空比雙次刷新電流環(huán)預(yù)測控制算法中，在a時(shí)刻進(jìn)行電流采樣，通過數(shù)字信號(hào)處理器(DSP)的模數(shù)轉(zhuǎn)換進(jìn)行坐標(biāo)變換，并與給定電流進(jìn)行比較;再通過電流環(huán)預(yù)測控制算法進(jìn)行控制，從而產(chǎn)生下一個(gè)控制周期起點(diǎn)(b時(shí)刻)的控制電壓[9];最后，進(jìn)行占空比的計(jì)算和PWM的更新.該過程雖然通過電流預(yù)測下一個(gè)控制周期的電壓抵消了電流采樣延時(shí)，但仍存在一個(gè)控制周期的延時(shí)[10]，即Td=0.5Tc.

2 復(fù)矢量解耦的電流環(huán)預(yù)測算法

本時(shí)刻采樣的電流通過預(yù)測控制算法可得到下一時(shí)刻的預(yù)測電壓,并作為電流環(huán)的輸出[11]，從而抵消采樣延時(shí)，減少控制延時(shí)，提高電流環(huán)響應(yīng)性能.通過對d-q軸電壓進(jìn)行復(fù)矢量解耦[12-13]，可進(jìn)一步提高電流環(huán)響應(yīng)性能.

2.1 電流環(huán)預(yù)測控制

電流環(huán)預(yù)測控制算法的數(shù)學(xué)模型有如下4點(diǎn)假設(shè):1) 忽略電機(jī)的鐵心飽和；2) 不計(jì)電機(jī)的渦流損耗和磁滯損耗；3) 轉(zhuǎn)子上沒有阻尼繞組，永磁體也無阻尼作用；4) 電機(jī)的感應(yīng)反電動(dòng)勢為正弦波.

永磁同步電機(jī)在旋轉(zhuǎn)坐標(biāo)系下的電壓方程[10]為

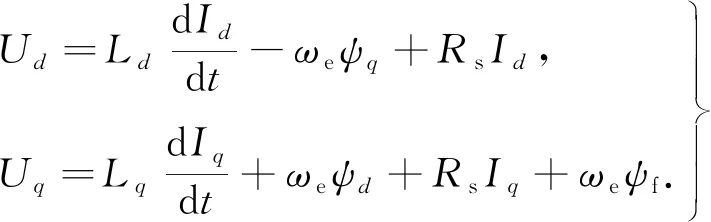
(5)

式(5)中：Ud為永磁同步電機(jī)的d軸電壓；Id為d軸電流；ψd，ψq分別為d軸磁鏈和q軸磁鏈；Ld，Lq分別為d軸電感和q軸電感.

在表貼式同步電機(jī)中，有Ld=Lq=Ls，由電壓方程可推出電流的狀態(tài)方程[10]為

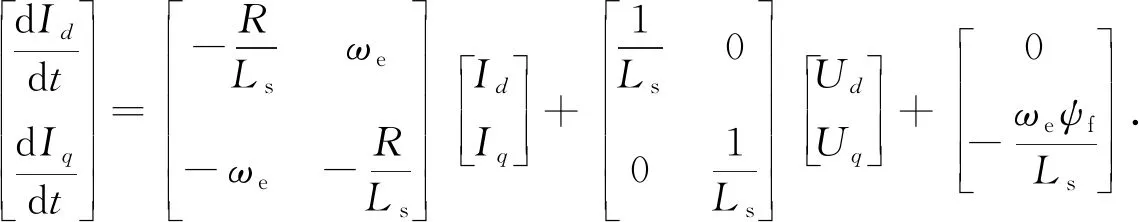
(6)

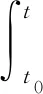
(7)

式(7)中：t0為初始時(shí)間；τ為時(shí)間變化值.

u在t0～t恒不變，設(shè)t0=kTs，t=(k+1)Ts[10]，Ts為采樣時(shí)間，可得

x(k+1)=Aφx(k)+A-1(Aφ-E)Bu(k)+A-1(Aφ-E)D(k).

(8)

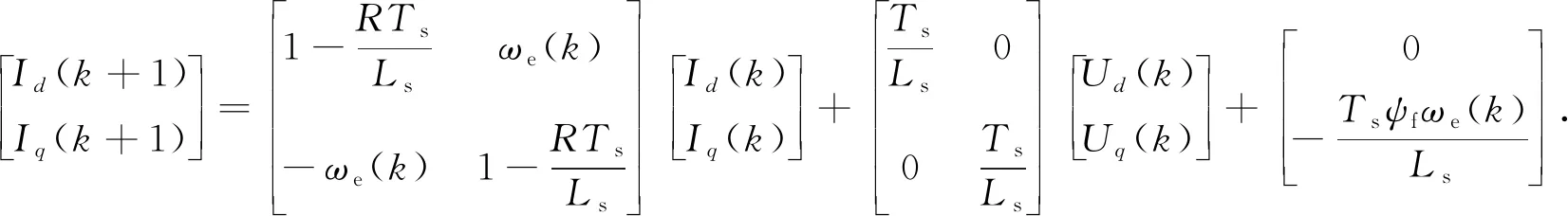
(9)

根據(jù)電流環(huán)預(yù)測控制原理，I(k+1)=I*(k+1)，故第k個(gè)周期的控制變量U(k)為

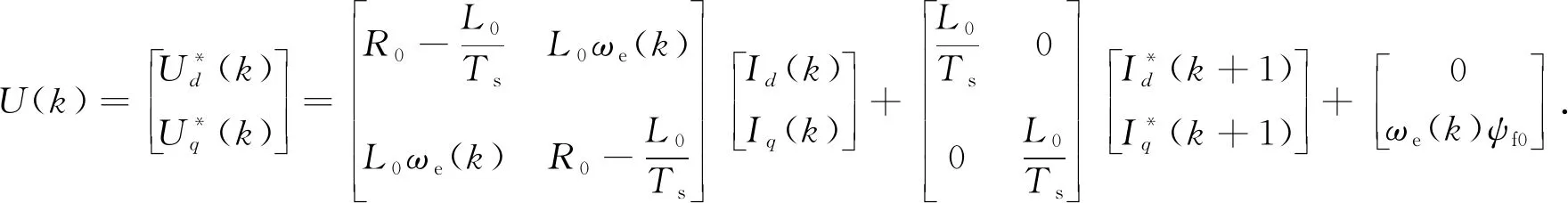
(10)

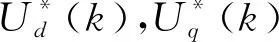
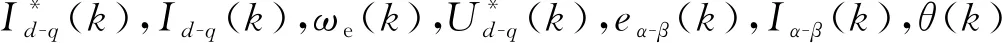
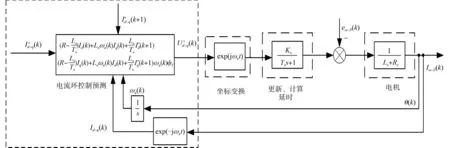
圖3 電流環(huán)預(yù)測控制算法的結(jié)構(gòu)框圖Fig.3 Structural block diagram of current loop predictive control algorithm

2.2 復(fù)矢量解耦控制

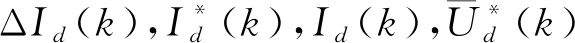
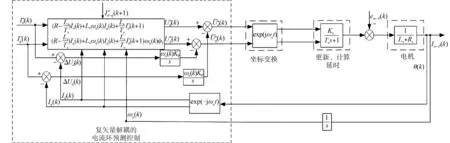
圖4 復(fù)矢量解耦的電流環(huán)預(yù)測控制算法的結(jié)構(gòu)框圖Fig.4 Structural block diagram of current loop predictive control algorithm of complex vector decoupling

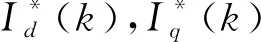
3 仿真實(shí)驗(yàn)分析

在Matlab/Simulink軟件中，采用PI控制算法和電流環(huán)預(yù)測控制算法進(jìn)行仿真.電機(jī)參數(shù):電機(jī)額定電流為6 A;額定轉(zhuǎn)速為2 000 r·min-1;額定轉(zhuǎn)矩為5 N·m；定子電阻為3.15 Ω；定子磁鏈為0.175 Wb；定子電感為0.008 5 H；電機(jī)極對數(shù)為4；轉(zhuǎn)動(dòng)慣量為0.008 kg·m2.

直流母線電壓為310 V，電流采樣頻率為20 kHz，載波頻率為10 kHz.在0時(shí)刻，速度給定為1 000 r·min-1的階躍指令，并在0.10 s時(shí)，突加5 N·m的恒定負(fù)載.三相電流和d-q軸電流波形均可反映交流伺服系統(tǒng)瞬態(tài)和穩(wěn)態(tài)的運(yùn)行情況.

PI控制算法和電流環(huán)預(yù)測控制算法下的三相電流和d-q軸電流，如圖5所示.圖5中:I為電流.由圖5(a)可知：PI控制算法的電流含有大量的諧波，這是由于該算法存在嚴(yán)重的滯后問題，波形中含有大量的噪聲導(dǎo)致波形成非正弦.由圖5(b)可知：電流環(huán)預(yù)測控制算法的三相電流波形基本為正弦波.由圖5(c)，(d)可知：當(dāng)0.10 s突加負(fù)載時(shí)，圖5(d)的d軸電流比圖5(c)的波動(dòng)更小；在穩(wěn)態(tài)情況下，無論電機(jī)空載或帶載，相較于PI控制算法，電流環(huán)預(yù)測控制算法的d-q軸電流波動(dòng)較小.

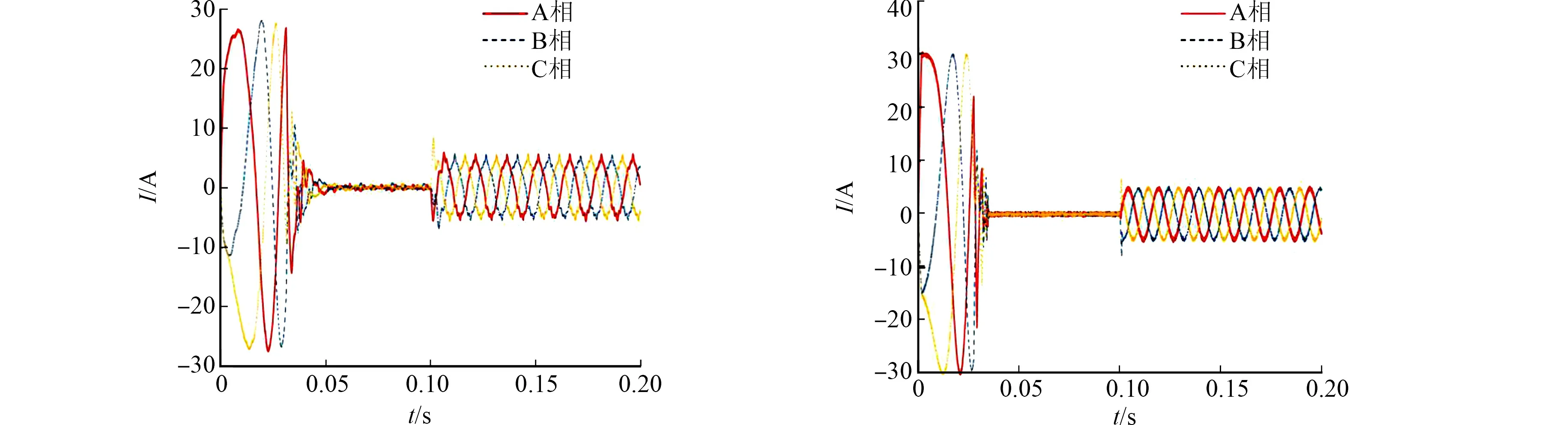
(a) 三相電流(PI控制算法) (b) 三相電流(電流環(huán)預(yù)測控制算法)

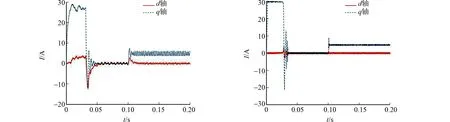
(c) d-q軸電流(PI控制算法) (d) d-q軸電流(電流環(huán)預(yù)測控制算法)圖5 不同算法的三相電流和d-q軸電流Fig.5 Three-phase current and d-q axis current of different algorithms

電流環(huán)預(yù)測控制算法的未解耦和解耦的d-q軸電流,如圖6所示.由圖6可知：d-q軸解耦和未解耦的d軸電流波形在電機(jī)啟動(dòng)時(shí)都有波動(dòng)，但解耦的d軸電流波動(dòng)較小;當(dāng)0.10 s突加負(fù)載時(shí),未解耦的d軸電流有1.2 A的跳動(dòng)，而解耦的電流基本保持恒定；解耦和未解耦的q軸電流基本沒有變化.因此，解耦對改善電流具有一定的作用.

圖7 不同算法的轉(zhuǎn)速響應(yīng)波形Fig.7 Rotational speed response waveform of different algorithms

PI控制算法(占空比單次刷新)的電流采樣頻率為10 kHz，PI控制算法(占空比雙次刷新)的采樣頻率為20 kHz，未解耦和解耦的電流環(huán)預(yù)測控制算法的電流采樣頻率皆為20 kHz，載波頻率皆為10 kHz.在0時(shí)刻，速度給定1 000 r·min-1的階躍指令，不同算法的轉(zhuǎn)速(ωe)響應(yīng)波形,如圖7所示.由圖7可知：PI控制算法(占空比單次刷新)的轉(zhuǎn)速響應(yīng)最慢，PI控制算法(占空比雙次刷新)的轉(zhuǎn)速響應(yīng)次之；未解耦的電流環(huán)預(yù)測控制算法的轉(zhuǎn)速響應(yīng)較快，解耦的電流環(huán)預(yù)測控制算法進(jìn)一步提高轉(zhuǎn)速響應(yīng).然而，轉(zhuǎn)速響應(yīng)波形在反映電流環(huán)響應(yīng)快慢方面具有一定的局限性，為了更精確地分析不同算法的電流環(huán)響應(yīng)速度，可以采用頻域分析方法.

從頻域的角度分析電流環(huán)響應(yīng)，閉環(huán)截止頻率越大，系統(tǒng)的瞬態(tài)響應(yīng)速度越快.向系統(tǒng)電流環(huán)d軸輸入幅值一定的正弦激勵(lì)，通過改變激勵(lì)的頻率，直至幅值衰減為最大值的0.707倍，此時(shí)，激勵(lì)的頻率為系統(tǒng)電流環(huán)的帶寬頻率(截止頻率).

在Simulink仿真軟件中，向電流環(huán)d軸輸入幅值為1 A的正弦激勵(lì)，通過改變激勵(lì)的頻率分別得到PI控制算法和電流環(huán)預(yù)測控制算法的電流環(huán)帶寬頻率.不同算法的d軸輸出響應(yīng)波形，如圖8所示.

由圖8可知:電流環(huán)d軸輸入正弦激勵(lì)的頻率分別為1 607,3 183,4 293,4 535 Hz，輸出響應(yīng)幅值均衰減為其最大值的0.707倍，解耦的電流環(huán)預(yù)測控制算法的電流環(huán)帶寬最寬，響應(yīng)最快.因此，從頻域角度分析也可得到相同的結(jié)論.

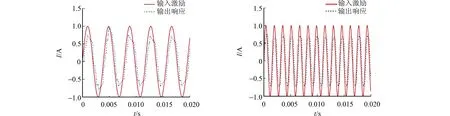
(a) PI控制算法(占空比單次刷新) (b) PI控制算法(占空比雙次刷新)

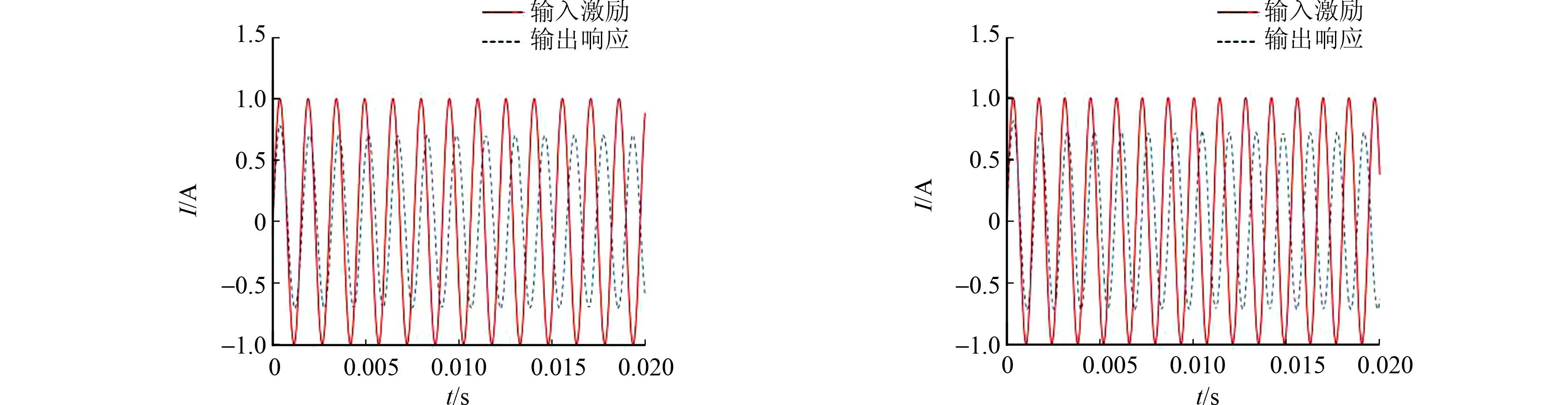
(c) 未解耦的電流環(huán)預(yù)測控制算法(占空比雙次刷新) (d) 解耦的電流環(huán)預(yù)測控制算法(占空比雙次刷新)圖8 不同算法的d軸輸出響應(yīng)波形Fig.8 d axis output response waveform of different algorithms

4 結(jié)束語

分析電壓輸出滯后、電流采樣延時(shí)和d-q軸電壓耦合等限制電流環(huán)帶寬提高的影響因素，針對不同的延時(shí)問題，采用不同的解決方法.采用一個(gè)控制周期內(nèi)占空比雙次刷新的方法，改善電壓輸出滯后問題；采用電流環(huán)預(yù)測控制算法，改善電流采樣延時(shí)問題；采用復(fù)矢量解耦控制的方法，解決d-q軸電壓耦合的問題.仿真實(shí)驗(yàn)結(jié)果表明：相較于PI控制算法，復(fù)矢量解耦的電流環(huán)預(yù)測控制算法能夠使電流環(huán)響應(yīng)得到改善.