基于最優滑移率的車輛軌跡跟蹤控制研究

孫會來 李研強 趙良柱 王永濤 王業森 趙佳俊

摘 要：為了實現智能車輛最優的軌跡跟蹤控制，最大程度的利用滑移率和地面附著系數實現智能車輛的動力學控制，文章提出了考慮滑移率的軌跡跟蹤控制方法。根據車輛行駛特性，建立動力學方程，計算運動過程中的輪速和橫擺角，并結合滑移率對車輛動力學的影響，基于最優滑移率設計了控制系統，以制動工況為例，實現制動車速工況下的最優控制。基于車輛二自由度模型，運用Matlab建立二維空間整車運動軌跡模型，得到車輛運動仿真軌跡。仿真結果驗證了數學模型的準確性和正確性。考慮滑移率和車輛動力學的軌跡跟蹤控制更具真實準確，文中數學模型及設計的控制系統對車輛跟蹤控制有參考價值。

關鍵詞：軌跡跟蹤控制;二自由度;滑移率

中圖分類號：V323 ?文獻標識碼：A ?文章編號：1671-7988（2020）09-61-04

Research on vehicle trajectory tracking control based on optimal slip ratio^*

Sun Huilai^1，2， Li Yanqiang¹， Zhao Liangzhu²， Wang Yongtao²， Wang Yesen²， Zhao Jiajun²

（?1.Institute of Automation， Qilu University of Technology （Shandong Academy of Sciences?），Shandong Jinan 250101; 2.College of Mechanical and Automotive Engineering， Qilu University of Technology（?Shandong?Academy?of?Sciences?）， Shandong Jinan 250353 ）

Abstract：?In order to achieve the optimal trajectory tracking control of intelligent vehicles， and to maximize the use of slip ratio and ground adhesion coefficient to achieve the dynamic control of intelligent vehicles， a trajectory tracking control method considering slip ratio is proposed in this paper. According to the driving characteristics of the vehicle， the dynamic equation is established， the wheel speed and yaw angle in the process of motion are calculated， and the control system is designed based on the optimal slip rate in combination with the influence of slip rate on the vehicle dynamics. Taking the braking condition as an example， the optimal control under the braking speed condition is realized. Based on the two degree of freedom model of vehicle， a two-dimensional space vehicle motion trajectory model is established by MATLAB， and the vehicle motion simulation trajectory is obtained. The simulation results verify the accuracy and correctness of the mathematical model. The track tracking control considering slip rate and vehicle dynamics is more real and accurate. The mathematical model and control system designed in this paper have reference value for vehicle tracking control.

Keywords：?Tracking control;?Two degree of freedom;?Wheel slip ratio

CLC NO.：?V323??Document Code： A??Article ID： 1671-7988（2020）09-61-04

前言

隨著工業自動化的迅速發展，無人駕駛車輛的應用逐漸被人們關注。基于環境感知的輔助駕駛技術或車輛全自動駕駛技術迅猛發展，以車輛自主修復既定軌跡成為核心技術之一。實現全自主無人駕駛車輛在高速等復雜路面安全穩定的軌跡跟蹤控制具有十分重要的意義。

根據軌跡跟蹤控制的技術研究背景，常見的控制方式有PID控制、自適應控制、預測控制、滑模控制等。例如余卓平^[1]研究的反步法差動轉向軌跡跟蹤著重考慮車輛動力學模型，并未建立二自由度模型。本文采取二自由度模型和車輛動力學模型相結合的方法更加準確直觀地實現了車輛軌跡跟蹤控制。再如潘世舉^[2]提出的跟蹤誤差法研究車輛軌跡及鄭子驁^[3]提出的反演法軌跡控制技術都沒有將車輛的滑移率考慮進去，與實際的車輛運動狀態有些許偏差。此外自主駕駛車輛在運動過程中受到摩擦和輪胎磨損的原因，在正常行駛時要考慮相應的動力學約束和滑移率等等因素。

因此本文將滑移率作為主要控制參數建立車輛動力學模型，通過仿真軟件MATLAB/Simulink搭建基于運動學模型的線性二自由度模型預測控制算法。線性二自由度模型預測控制算法相比于非線性模型預測控制算法具有實時性好、計算簡便、結果明了等優點，通過Simulink搭建基于運動學模型的線性二自由度模型預測控制算法，同時考慮了相同的控制參數在對不同車輛初始位姿下的軌跡跟蹤控制效果也略有不同，因此結合PID控制，優化滑移率以提高車輛的軌跡跟蹤精度，并選取了最有代表性的制動工況進行仿真分析。

1 二自由度模型及車輛動力學模型

1.1 車輛線性二自由度模型

本文的研究是基于二自由度模型，考慮滑移率對車輛運動軌跡的影響，并求解出該車的運動微分方程。根據汽車真實運動規律，結合PID控制運用MATLAB建立一個二維空間整車運動軌跡模型。

模型的假設條件：

（1）忽略車輪、車體和地面的彈性作用;

（2）忽略車輛的俯仰、側傾和垂向運動;

（3）車輛沿X軸的前進速度u視為恒定值;

（4）側向加速度限定在0.4g以下;

（5）不考慮地面的切向力對輪胎側偏特性的影響;

（6）忽略空氣阻力和滾動阻力的影響;

（7）不考慮載荷轉移，車輛的質量均勻分布在每個車輪上。

這樣，車輛被簡化成一個單輪車模型。該模型具有側向及橫擺兩個自由度。

如圖1所示，車輛坐標系的縱軸和橫軸分別對應圖中的OX軸 和OY軸。在 t 時刻質心的速度 v₁在 OX軸、OY 軸上的分量分別是 u、v。因為車輛在轉向過程中通常會伴隨著平移和轉動兩種動作，所以車輛坐標系中的質心速度的大小和方向均發生變化，導致體現在車輛坐標系中的縱軸與橫軸數值也會隨之發生變化。由此可推導出車輛在絕對慣性坐標系下的運動方程：

式中φ為車輛的橫擺角度，且。

1.2 汽車動力學模型

汽車制動時，隨著制動時間的不斷增加，由于車輪抱死，車輪運動中，滾動占比會越來越少，同時滑動占比將越來越多。

由于汽車動力學模型的建立是一個復雜的過程，所以采用單輪模型建立汽車動力學模型。簡化的單輪模型如圖2所示。

由圖可得到車輛的動力方程：

車輛運動方程：

車輪運動方程：

車輛縱向摩擦力：

滑移率的定義：

式中，m為1/4整車質量（kg）;F為地面制動力（N）;R為車輪半徑（m）;I為車輪轉動慣量（kg·m²）;Tb為制動力矩（N·m）;v 為車身速度（m/s）;ω為車輪角速度（rad·s）;N為地面對車輪的法向反作用力（N）;μ為地面摩擦系數，v為車輪中心的速度;r為車輪的滾動半徑。

1.3 汽車輪胎制動模型

汽車輪胎模型反映了車輪和地面附著系數與滑移率之間的關系。常見的輪胎模型有雙線性模型、Burckhardt輪胎模型和Dugoff輪胎模型等。本文采取應用比較廣泛的雙線性輪胎模型，將附著系數—滑移率曲線簡化為兩段直線。如圖3所示：

汽車制動器模型是指制動系氣液壓力與制動器力矩之間的關系模型。為了便于研究，假設仿真的制動器為理想原件，忽略制動器滯后帶來的影響。因此建立制動器方程如下：

式中，Tb為制動器制動力矩（N·m）;K_f為制動器制動因數（N·m/kPa）;P為制動壓力（kPa）。

由于制動器中各個機械零部件存在間隙和摩擦，導致制動器滯后，建立制動器滯后系統模型如下：

2 基于二自由度模型的MATLAB/SIMULINK仿真

2.1 控制系統的設計

本文主要研究基于最優滑移率的車輛軌跡控制，采用Simulink及有關的控制工具箱進行最優滑移率與不考慮滑移率之間對比以及最優滑移率與不考慮車輛動力學之間的對比的仿真分析，得到車輛軌跡的仿真對比圖以及車速輪速的對比圖，以突出最優滑移率對軌跡控制的優異性。

模型系統一共分為三大部分，第一部分為被控制對象，也就是車輛動力學模型;第二部分是汽車運動學模型，在實際情況中，車速受很多其他因素的影響，不能對其直接控制，所以我們只能依靠調節滑移率，從而控制輪速，車速只能通過閉環控制：利用滑移率的定義求得實際滑移率，然后與期望滑移率進行對比，再進行閉環控制，進而控制車速。對制動滑移率的控制就是使制動時滑移率維持在最佳滑移率附近（10%～?30%），以得到最短的制動距離。控制器最常用的算法就是利用比例積分微分控制P，只要調整的PID參數合適，就可以得到很好的控制效果;第三部分是汽車轉向模型，給予車輛一個角度（通過方向盤實現），利用PID控制^[4]實現對汽車轉向的控制，對車輪轉角進行二自由度轉化，分別在X軸和Y軸顯示相對應的角度，然后與對應的車速相乘，橫向和縱向車輛軌跡圖，最終實現對車輛的軌跡控制。

2.2 仿真模型建立

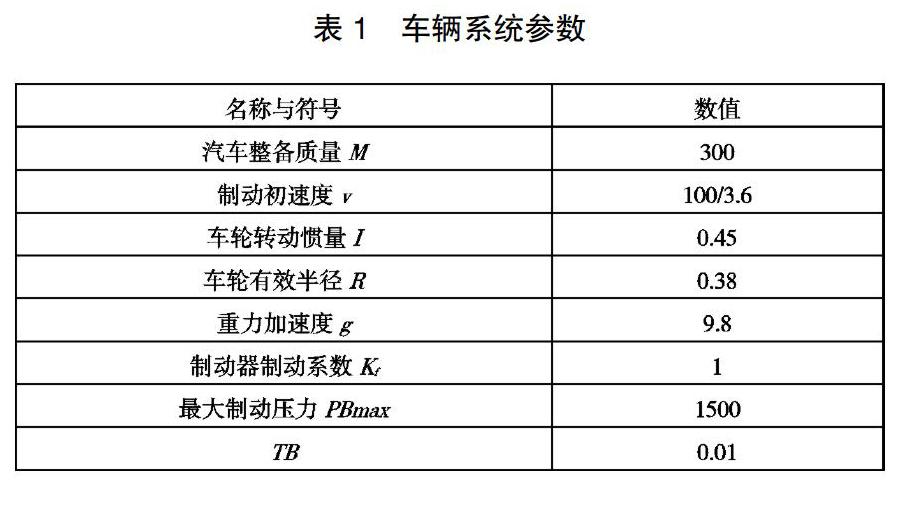
Simulink是MATLAB中的一種可視化仿真工具， 是一種基于MATLAB的框圖設計環境，是實現動態系統建模、仿真和分析的一個軟件包。利用Simulink搭建車輛軌跡控制的仿真模型，該軌跡跟蹤控制車輛系統參數見表1。將前輪轉角作為系統輸入量，可以使車輛的運動狀態得到更方便的控制，讓車輛盡可能地跟隨預期的軌跡行駛。由此，可以建立Simulink仿真流程（如圖4所示）。

3 仿真結果分析

3.1 二維軌跡仿真

根據車輛參數進行仿真，最佳滑移率設置為 0.2，整車1/4質量為300kg，初始車速為100km/h，以車輛前進方向為X軸，平行于地面、垂直于前進方向為Y軸，輸入期望軌跡角度為此直角坐標系的45°。

由圖5知：相比于不考慮滑移率的控制，考慮滑移率控制的車輛軌跡更加平滑、剎車距離更短，這是因為閉環控制穩定的將滑移率控制在10%～30%，使得車輛始終保持較好的車身狀態。

文中還將最優軌跡與不考慮車輛動力學的車輛軌跡進行對比，在不考慮車輛動力學的仿真模型中，僅簡單的將車速作為一個輸入變量，經過PID控制進行仿真。兩者對比可以看出考慮動力學的仿真模型更切合實際情況。

在初始車速為100公里每小時的前提下，車輛經過7.7秒完全停止。且輪速線一直處于車速線下方并靠近車速線，最終在7.7秒兩者同時為零。

3.2 車輛運動學仿真

本文一大特點就是加入一個角度輸入量并利用二自由度轉化，生成車輛運動軌跡，圖8就是軌跡轉角圖。

由圖9可知：實際滑移率始的數值終維持在0.2附近波動，符合期望的滑移率。說明了本文的PID控制器發揮了較好的調節作用。

3.3 車輛動力學仿真

由圖10可知：制動力在閉環控制中受到最優滑移率控制的影響，最終在480N上下波動。

4 結語

本文通過對車輛進行力學分析，求解出車輛的動力學及運動學模型;利用MATLAB中的Simulink模塊搭建基于二自由度轉化的車輛制動系統的模型，并進行了仿真測試;通過對比分析可知：考慮滑移率的車輛行駛軌跡更接近真實情況，PID控制的使用大大縮短了制動距離，兩者相結合使車輛運動軌跡更加符合預期。對于車輛跟蹤控制的研究具有理論研究價值與參考意義。

參考文獻

[1] 余卓平，侯譽燁，熊璐，陳素琴.基于反步法的差動轉向無人車輛軌跡跟蹤[J].汽車工程，2019，41（11）：1229-1234+1242.

[2] 潘世舉，李華，蘇致遠，徐友春.基于跟蹤誤差模型的智能車輛軌跡跟蹤方法[J].汽車工程，2019，41（09）：1021-1027.

[3] 鄭子驁.基于反演法的智能汽車連續換道軌跡控制技術[J].自動化與儀器表，2019（01）：129-131.

[4] 秦萬軍，徐友春，李明喜，耿帥，李欣瑩.基于二自由度模型的無人駕駛車輛軌跡跟蹤控制研究[J].軍事交通學院學報，2014，16（11）：31- 35.

[5] 趙垚森，朱勇，徐小東.基于Simulink的汽車ABS仿真分析[J].機電工程，2018，35（12）：1357-1360.

[6] 馬迪.自主駕駛車輛軌跡跟蹤控制研究[D].大連理工大學，2017.

[7] 喻青濤.基于差力主動轉向的電動輪車耦合動力學控制研究[D].重慶理工大學，2016.

[8] 李志高.汽車ABS的控制算法與仿真研究[D].武漢理工大學，2011.

[9] 冉洪亮.基于模型預測控制算法的無人駕駛車輛路徑識別與跟蹤控制[D].重慶大學，2018.

[10] 李子龍.基于人工神經網絡的智能汽車循跡控制研究[D].合肥工業大學，2019.

[11] 程軍.用MATLAB/SIMULINK進行車輛控制系統的設計[J].汽車研究與開發，1997（03）：7-10+24.

[12] 劉鑫.發電機線棒壓孔機計算機監控系統的研發與應用[D].大連交通大學，2011.