一個函數不等式恒成立問題的兩種解法
曹 彬
(貴州省黔西第一中學 551500)
函數作為高中數學知識體系的核心,是歷年高考的熱點,函數題常常作為高考壓軸題出現.以研究函數性質為主要解題手段的不等式稱為函數不等式,函數不等式恒成立問題是高考函數題中的重點,在高考試卷上較為常見.通常以一次函數、二次函數、三角函數、指數與對數函數為載體,考察函數的圖象與性質,滲透換元、轉化與化歸、數形結合、函數與方程等思想方法,考查學生的綜合解題能力,在培養思維的靈活性、創新性,發展學生數學核心素養起到積極的作用.
函數不等式恒成立問題都要轉化為函數最值問題,但對于解析式較復雜的函數,學生普遍感到難以找到解決問題的切入點和突破口.本文旨在介紹洛必達法則應用的同時,多種解法求一類特殊函數不等式恒成立問題中參數取值范圍.
一、問題的提出
已知函數f(x)=(x+1)lnx-a(x-1),若對任意x∈(1,+∞),都有f(x)>0恒成立,求常數a的取值范圍.
這種問題通常轉化成討論f(x)在(1,+∞)上的最小值,而且常常用參變分離方法.如果仔細觀察,會發現f(1)=0,這種問題的解法就有數形結合法、參變分離法,下面分別介紹這兩種解法.
二、問題的解答
1.解法一(數形結合法)
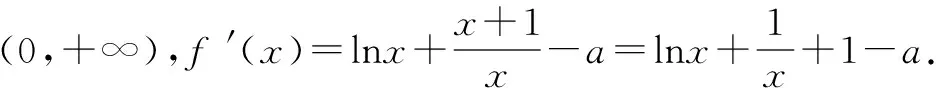
因為x>1,所以g′(x)>0恒成立,所以g(x)在(1,+∞)上為單調增函數,且g(1)=f′(1)=2-a.
當2-a≥0,即a≤2時,f′(x)>0在(1,+∞)上恒成立,所以f(x)在(1,+∞)上為單調增函數.由于f(1)=0,故滿足f(x)>0在(1,+∞)上恒成立.
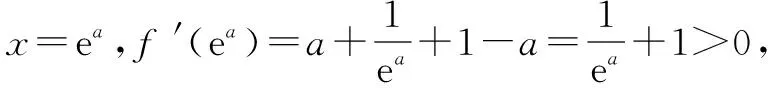
綜上,a≤2.
評析這種解法就是參考答案給出的常規解法,根據函數的性質確定函數的圖象,通過討論函數在指定范圍內是否有零點,逐步縮小參數的范圍并最終確定,但是找區間的端點是難點.
2.解法二(參變分離法)
洛必達法則 設函數f(x)和g(x)滿足:
(2)函數f(x),g(x)在x0的某個去心鄰域內可導,且g′(x)≠0;
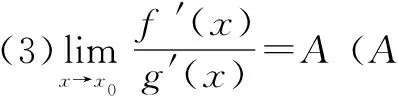
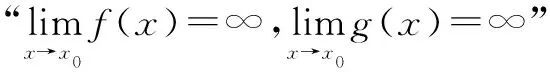
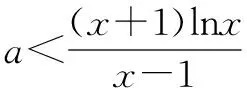
評析這是最容易找到入手點的解法,但在最后階段卻出現疑惑,因為在x=1處的函數值不能直接解出,所以要用洛必達法則求極限值.
運用上述兩種解法,可解決如下同類型題:已知函數f(x)=(1-x2)ex,當x≥0時,都有f(x)≤ax+1恒成立,求a的取值范圍.
函數題的得分率歷來不高,學生普遍感到困難,分析有如下原因:需要對證明的等式或者不等式進行變形,此過程需要技巧,經驗性很高,學生一般很難掌握;含有參數的問題需要分類討論,討論的類別較多,運算量大還容易遺漏;對研究的函數不能畫出圖象,難以構造出直觀模型輔助思考;很多函數題需要多次求導.
所以,如果用高中知識解答高考函數題,對學生的思考靈活性、思維嚴密性、表達邏輯性等方面的要求較高,難度較大.

