一種基于隨機序列的正交離散頻率編碼信號*

賈基東 李淑秋 李 宇

(1 中國科學院聲學研究所 北京 100190)

(2 中國科學院大學 北京 100049)

(3 中國科學院先進水下信息技術重點實驗室 北京 100190)

0 引言

探潛技術與潛艇隱身技術是水下目標探測中的矛與盾，為了提高探測能力，聲吶的發展經歷了從單水聽器到多元陣列、從窄帶處理到寬帶處理的過程。隨著多基地聲吶、水下傳感器網絡、多輸入多輸出(Multi input multi output，MIMO)聲吶等新型聲吶的出現，聲吶技術開始向分布式、空間分集的方向發展[1-3]。匹配濾波技術是主動聲吶接收端常采用的一種算法，為避免分布式系統中各發射信號在接收端彼此形成干擾，實現空間分集要求發射正交信號。

在通信中，設計正交信號的方法有時間分集、頻率分集、波形分集。在水下探測中，時間分集意味著低探測效率，頻率分集意為著低帶寬利用率，因此波形分集是一個最好的選擇。實現波形分集的一種常用方法是頻率調制，離散頻率編碼信號因為其模糊函數的一些特性而引起了人們的廣泛關注[4-6]。

離散頻率編碼信號彼此間的正交性好壞與頻率編碼序列密切相關。目前關于構造頻率編碼序列的方法研究主要分為兩類：一類是基于有限域和本原元理論的方法[7-12]，另一類是基于混沌序列的方法[13-17]。文獻[7]中作者定義了一種漢明相關函數來描述序列間的正交性，并給出了基于有限域和本原元理論設計頻率編碼序列的漢明相關理論下界。本文在仿真分析部分也將采用漢明相關函數來比較本文算法與對比算法的優劣。文獻[8]中作者基于代數結構設計了一種素數碼長序列的生成方法，并推導了信號的模糊函數。在文獻[12]中作者將基于有限域理論設計的編碼序列長度推廣為素數的倍數。盡管如此，基于有限域理論的編碼序列長度只能是某些值仍是這類方法的一大缺點，嚴重限制了其在實際應用中的價值。相比之下，能生成任意長度序列的基于混沌序列的設計方法則更為實用。文獻[14]中作者將Logistic 混沌序列映射為跳頻序列，并分析了序列的漢明相關性。在文獻[16]中，作者分析討論了基于幾種混沌序列設計的離散頻率編碼信號在模糊函數、正交性上的優劣，得出Bernoulli 混沌序列在離散頻率編碼信號設計中性能較好的結論。文獻[17]中作者將線性調頻信號應用到基于Lorenz 混沌的頻率編碼信號內部構造中，改善了信號的自相關性能。基于混沌序列能夠設計任意長度、任意數量的編碼序列集，但混沌序列表現出的隨機性并不夠強。

設計正交離散頻率編碼序列的關鍵是使碼元的隨機性足夠好，因此本文將生成偽隨機數的線性同余法應用于頻率編碼序列的構造，設計了一種基于隨機序列的正交離散頻率編碼信號，并與文獻[16—17]中的方法進行比較，得出了一些有用的結論。

1 離散頻率編碼信號

假設信號的一個編碼序列為Q={q0，q1，···，qN-1}，Q為序列Q0={1，2，···，N}的一個排列，Q0對應的信號頻率序列為F0={f0，f1，···，fN-1}，與Q相對應的信號頻率序列為F={f0，f1，···，fN-1}，則碼元到頻率的映射關系為

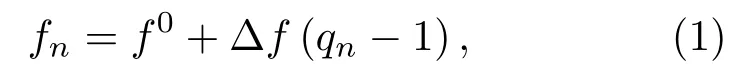
其中，f0為信號的載頻，Δf=fi+1-fi為編碼的步進頻率，如圖1所示。

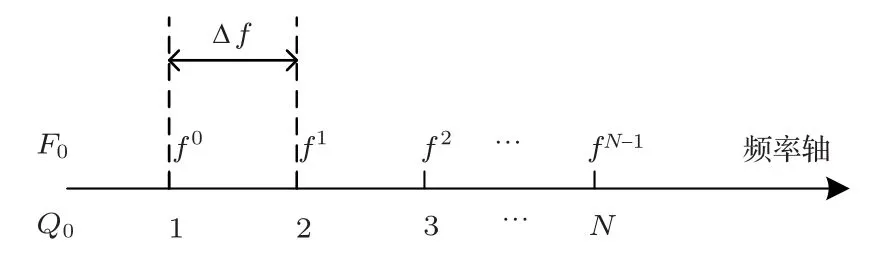
圖1 頻率序列到編碼序列的映射關系Fig.1 The relationship of the frequency sequence and the coding sequence

離散頻率編碼信號的數學模型可以描述為

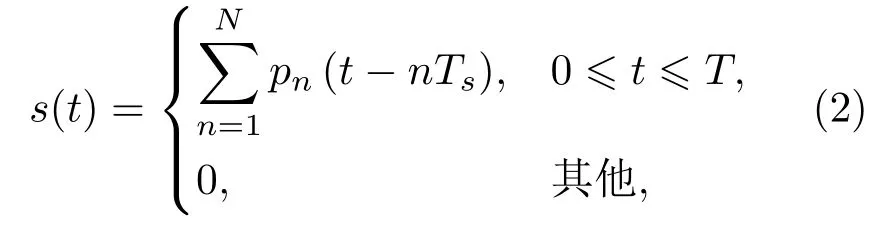
其中，T表示信號總時長，N表示編碼序列長度，Ts=T/N表示子脈沖時長，pn(t)表示單個碼元對應的子脈沖，表示為

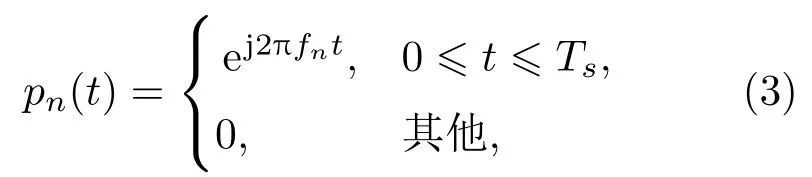
其中，fn表示與碼元mn相對應的子脈沖頻率。

2 正交頻率編碼集

2.1 Lorenz混沌序列

Lorenz 混沌是一種連續時間混沌系統，由美國著名的氣象學家Lorenz 提出，可描述為如式(4)的方程組[17]：

當式(4)中3 個參數σ、r、b滿足如式(5)時，Lorenz系統會出現混沌解。

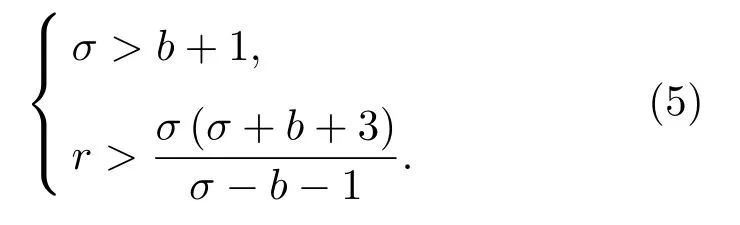
采用四階龍格庫塔法求解Lorenz方程組，設定采樣率為2000 Hz，可得到3 個狀態變量x(t)、y(t)、z(t)的采樣序列。圖2是一個Lorenz 系統的三維演示圖，其狀態軌跡反復折疊形成一個類似蝴蝶的圖形，在3 個維度上均有界，吸引子上也沒有交叉點，表現出整體混沌局部穩定的特點。圖3是Lorenz系統3個狀態變量的時間序列，3個序列均表現出非周期性和對初值的敏感性，當初值出現很小的變化時所得到的時間序列就出現很大的變化。變量x(t)的采樣序列在信號處理特性上優于y(t)和z(t)，因此在構造正交編碼時通常采用x(t)的采樣序列。

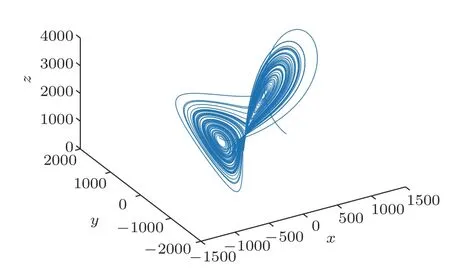
圖2 Lorenz 混沌運動軌跡Fig.2 The movement of the Lorenz chaos

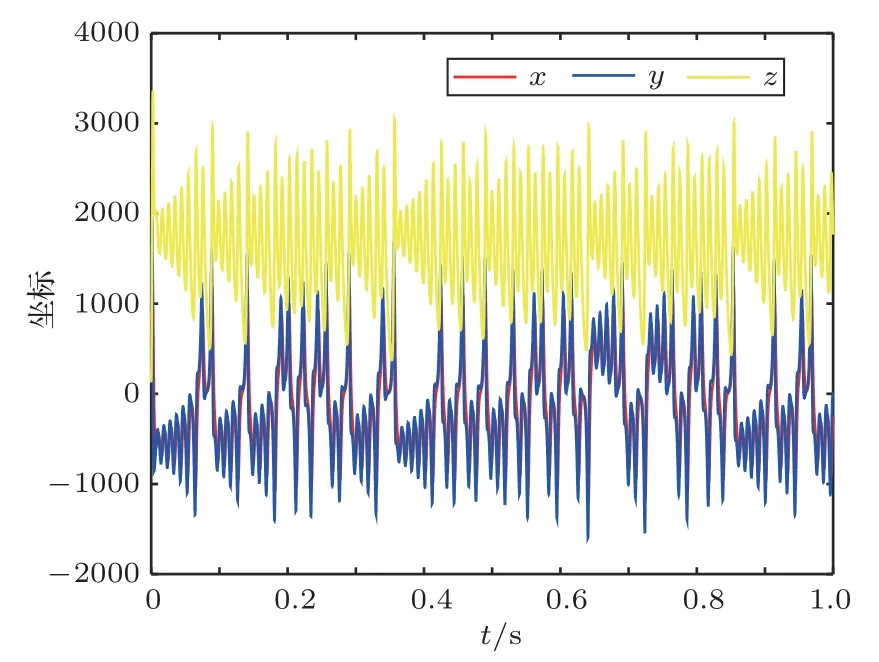
圖3 Lorenz 混沌3 個狀態變量的時間序列Fig.3 The time sequence of three states in the Lorenz chaos

2.2 Bernoulli混沌序列

Bernoulli 混沌是一種離散時間混沌系統，可描述為如式(6)的更新方程[16]：

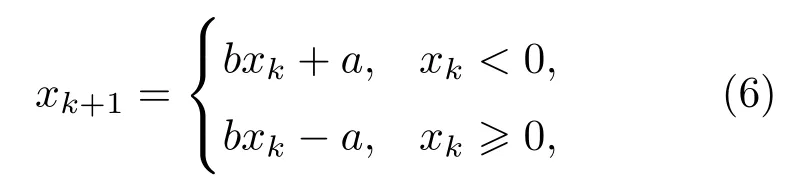
其中，a、b為混沌映射參數，a=0.5，b=2-ε，ε為一接近于0 的極小正值。xk∈[-0.5，0.5)為過程變量，b值越接近2，混沌序列值在混沌吸引域[-0.5，0.5)的遍歷性越好，一組Bernoulli混沌序列如圖4所示。

圖4 Bernoulli 混沌序列Fig.4 The time sequence of the Bernoulli chaos

2.3 隨機序列

線性同余法是一種簡單常用的均勻隨機數生成器，其遞推式表述為

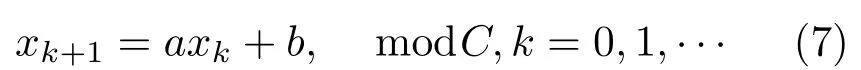
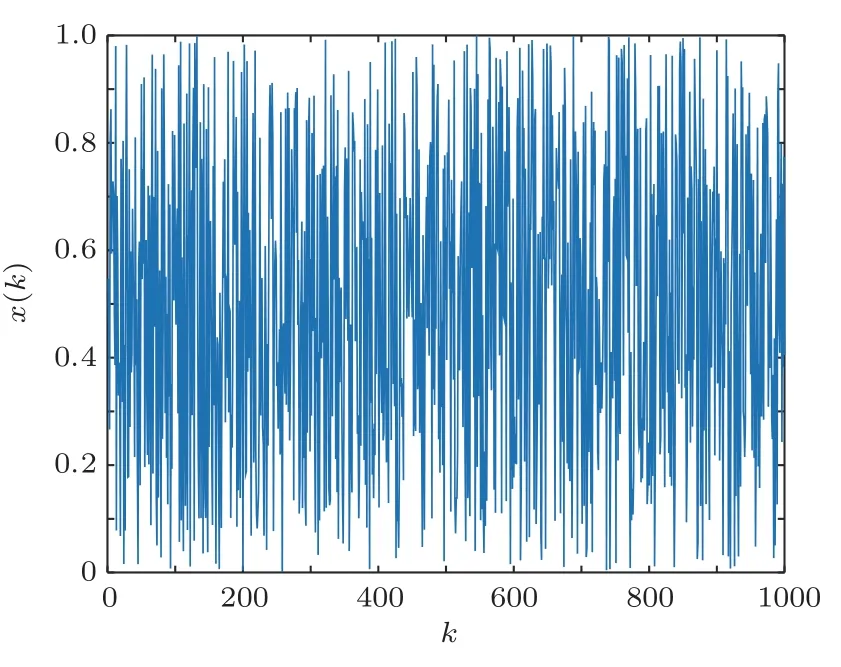
圖5 線性同余隨機序列Fig.5 The random sequence of the linear congruential generator

其中，參數a、b、C分別稱為乘子、增量和模。關于參數的選取已有許多的研究，一個十分著名的隨機數發生器是[18]

這種參數選取方法的主要考慮是便于計算機實現和受平方根準則的影響，該參數取值下的一組線性同余隨機序列如圖5所示。

2.4 正交頻率編碼集的構造

假設由混沌系統或隨機過程產生的混沌序列或隨機序列為{x0，x1，···，xi，···}，從中截取M段長度為N點的序列，表示為

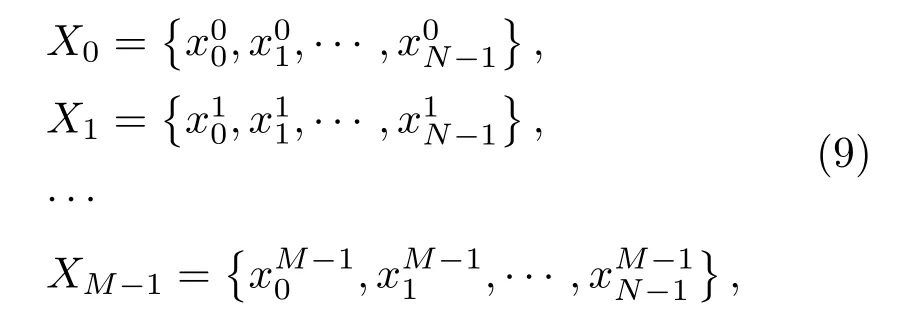
其中，M表示信號集中的信號總數，N表示單個信號的編碼長度。

對于混沌信號，由于初值的影響和臨近序列間的相關性較強，通常在截取時會采用拋棄混沌序列前面的一段和間隔截取兩種手段來提高信號間的正交性。對于隨機序列，由于各個時刻的隨機變量在統計上都獨立同分布，因此不存在這些問題。

對于第m段序列Xm，不妨按從小到大的順序對其進行排列，得到排序后的新序列為

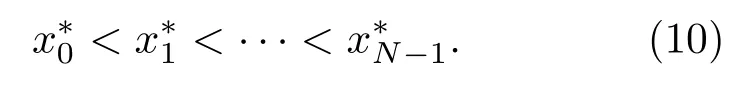
新序列中各元素在原序列中的位置索引構成的序列為

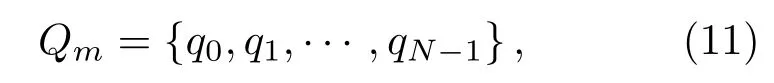
則序列Qm即為第m個信號的頻率編碼。

從截取后的混沌序列或隨機序列到最終信號的頻率序列間的映射關系可表示為

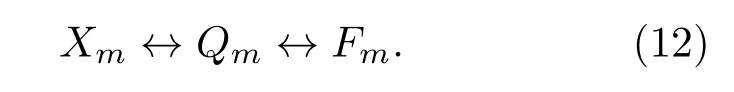
3 性能分析

信號的模糊函數描述了信號的時頻域聯合特性，模糊度圖則反映了目標距離、速度的測量精度，下面分別對此進行分析。

3.1 模糊函數

信號s(t)的時延多普勒模糊函數定義為[8，19]

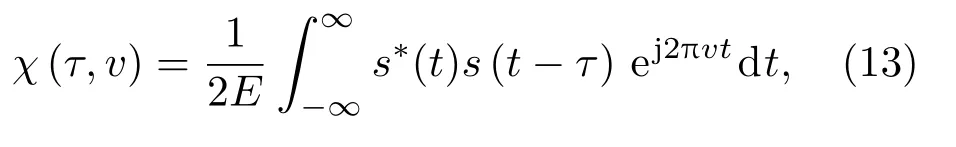
其中，τ表示時延，v表示多普勒頻移，*表示共軛運算，E表示信號s(t)的總能量，如式(14)所示：

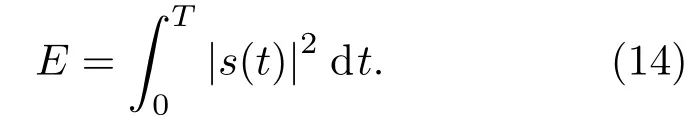
將式(2)、式(3)帶入式(14)，得到

將式(2)、式(15)代入式(13)，得到

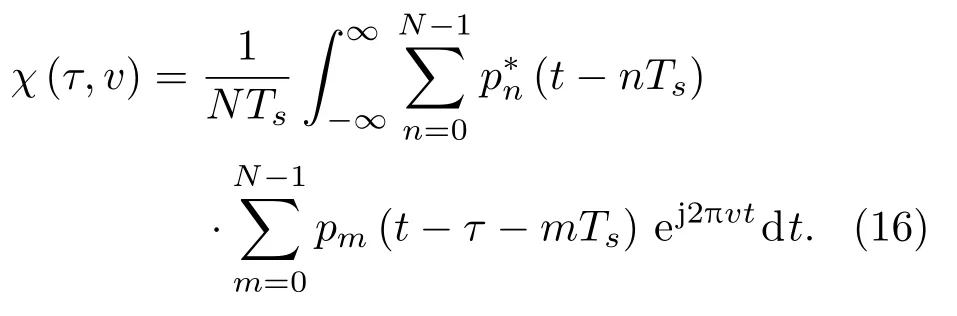
定義子脈沖的互模糊函數：

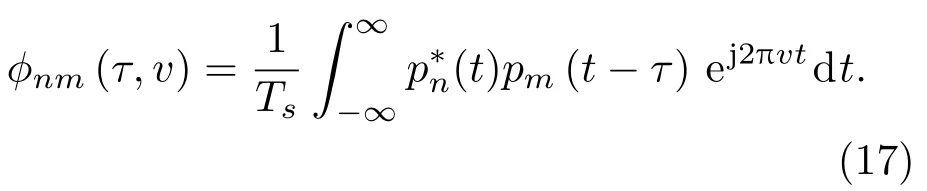
代入式(3)，得到

其中，α=fn-fm-v。

令m=n，則得到子脈沖的自模糊函數：

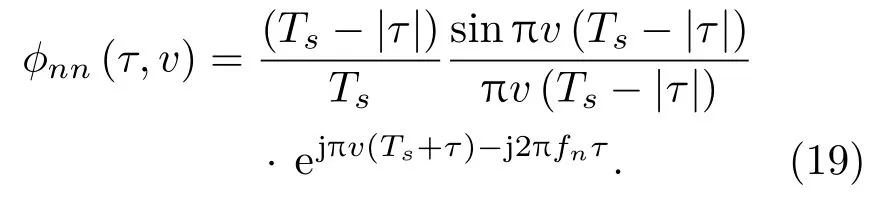
注意式(18)、式(19)均為|τ|≤Ts的情況，當|τ|＞Ts時，

重新考慮式(16)，則可以將其表述為

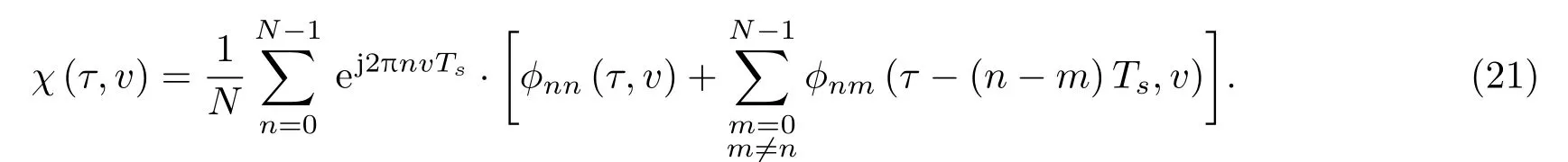
3.2 時延、頻移測量精度

將信號的模糊函數下降到最大值0.707 倍(-3 dB)處的截面圖定義為模糊橢圓或信號的模糊度圖，反映了目標距離、速度的測量精度。

令τ= 0，有φnm(0，v)= 0，因此信號的模糊函數可以表示為

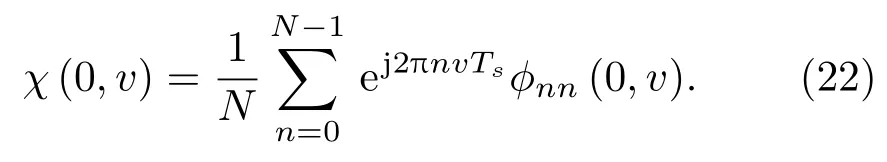
考慮到如式(23)的變換：

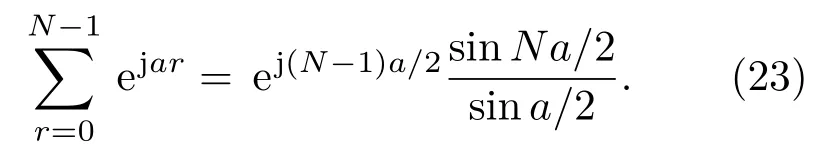
代入式(19)，得到

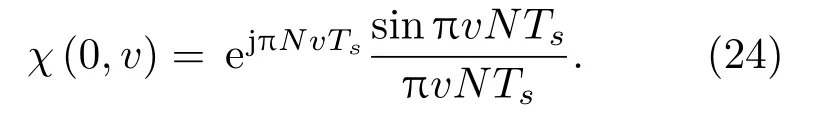
兩邊取模，有

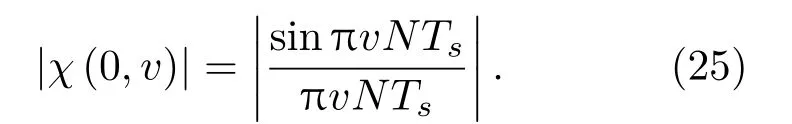
從式(25)可以看出，離散頻率編碼信號模糊函數在τ= 0 的平面表現為sinc 函數形式，信號的頻移測量精度只與信號總時長T=NTs有關。|χ(0，v)|的第一個零點位置為±1/T，定義以模糊度圖與頻移軸兩個交點間頻移差的一半為頻移測量精度，則信號的多普勒頻移測量精度為

即信號的多普勒測量精度與信號時長成反比。

令v=0，由式(1)可得

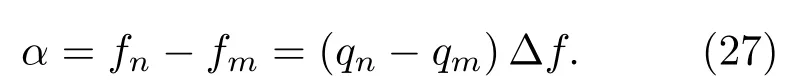
將式(27)代入到式(18)，得到

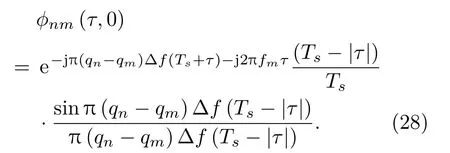
當τ →0時，其中sinc項

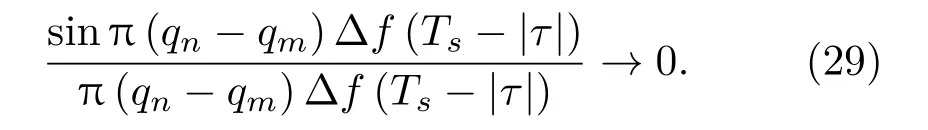
因此，當τ →0時

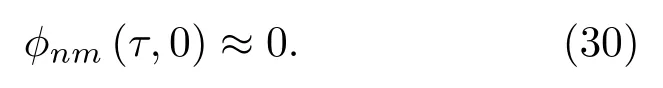
則信號的模糊函數可以近似表示為

代入式(19)，得到

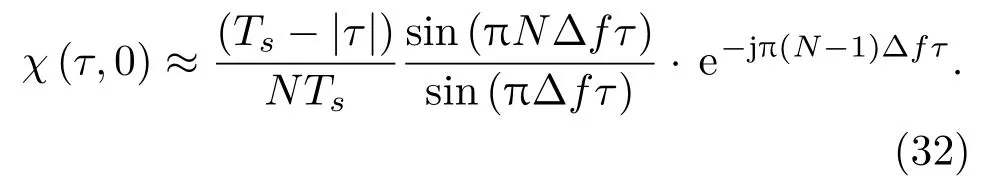
兩邊取模，有

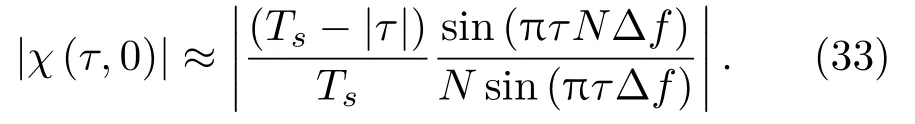
從式(33)可知，離散頻率編碼信號模糊函數的時延測量精度與信號的總帶寬B=NΔf有關。|χ(τ，0)|第一個零點的位置為±Ts/N，定義以模糊度圖與時延軸兩個交點間時延差的一半為時延測量精度，則信號的時延測量精度為

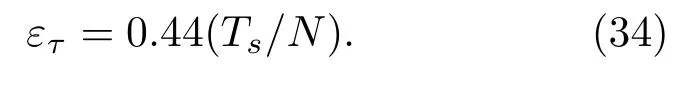
當TsΔf ≈1時，則

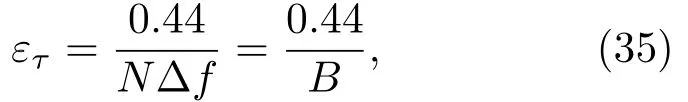
即信號的時延測量精度與信號帶寬成反比。

由式(26)和式(35)可知，離散頻率編碼信號的頻移測量精度和時延測量精度只與信號的時長和帶寬有關，而與具體的編碼序列無關。因此，對于正交離散頻率編碼信號集的設計，應該主要關注信號間的正交性設計，通過設計正交的頻率編碼序列，來提高信號間的正交性能。

3.3 正交性分析

假定由兩個長度都為N的不同序列Qx，Qy編碼得到的兩個信號分別為sx(t)、sy(t)，則兩個信號的互模糊函數定義為

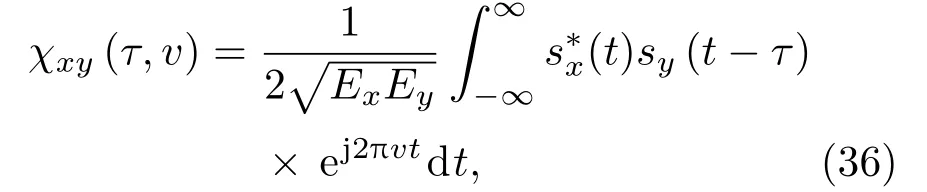
其中，Ex、Ey分別為信號sx(t)、sy(t)的能量大小。將式(2)、(3)代入式(36)，得到

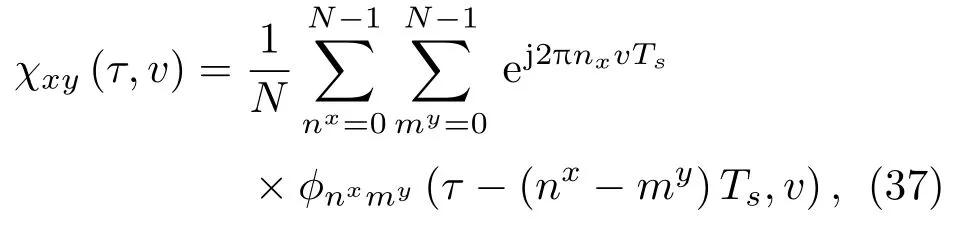
其中，

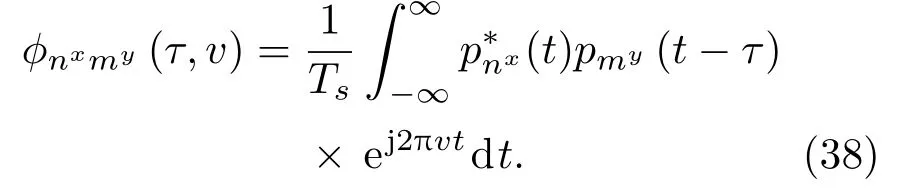
由3.1 節、3.2 節的分析可知，當nxmy時，φnxmy(τ，v)對χxy(τ，v)的貢獻很小，χxy(τ，v)中的峰值都主要來自于nx=my時φnxmy(τ，v)貢獻的能量，即當編碼序列Qx，Qy中的相同碼元在時域重疊時會使互模糊函數產生峰值，重疊的相同碼元越多，峰值越高。因此，對于自模糊函數來說，只要編碼序列是滿碼序列(每個碼元都在序列中出現且僅出現一次)，自模糊函數就能表現為近似理想的“圖釘型”函數。對于互模糊函數來說，則要設計盡可能不會出現碼元重疊的序列，來使不同離散頻率編碼信號間有足夠好的正交性。

對于隨機序列，由于在任意不同時刻都互不相關，因此在任一時延下兩個不同序列相同碼元重疊的概率都很小，即

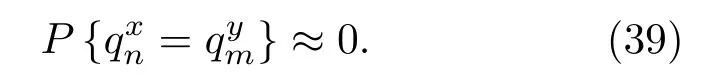
因此，信號sx(t)、sy(t)的互模糊函數

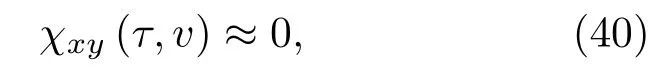
即信號sx(t)、sy(t)彼此間正交。

4 仿真分析與討論

按照上述第3節所描述的離散頻率編碼序列的生成方法，分別基于Lorenz 混沌序列、Bernoulli 混沌序列和隨機序列設計離散頻率編碼序列。碼長25、編碼數為2 時3 種方法各自生成的編碼序列如表1所示。設定采樣率為10 kHz，信號時長為1 s，帶寬為1 kHz，信號載頻為500 Hz，相應離散頻率編碼信號的自模糊函數和互模糊函數如圖6所示。從中可以看出，3 種方法設計的離散頻率編碼信號均具有“圖釘狀”的理想自模糊函數，且互模糊函數峰值都較小，而基于隨機序列編碼的信號相比另外兩種方法設計的信號互模糊函數峰值更小。

截取圖6中3 種設計方法得到信號的自模糊函數的v= 0 平面和τ= 0 平面，分別得到3 種設計方法的時延相關函數和多普勒相關函數，如圖7所示。從中可以看出，3 種信號時延相關函數和多普勒相關函數的主瓣基本重合，即3 種方法設計的信號具有相同的時延測量精度和多普勒測量精度，這是因為盡管3 種設計方法得到的信號編碼序列不同，但所采用的信號時長和信號帶寬均相同。這與3.2 節對于離散頻率編碼信號的時延測量精度和多普勒測量精度的理論分析結果一致，即信號的時延測量精度與信號帶寬成反比，信號的多普勒測量精度與信號時長成反比。3 種設計方法采用了相同的信號時長和信號帶寬，因此具有相同的時延測量精度和多普勒測量精度，表現在時延相關函數上和多普勒相關函數上即各自的主瓣基本重合。

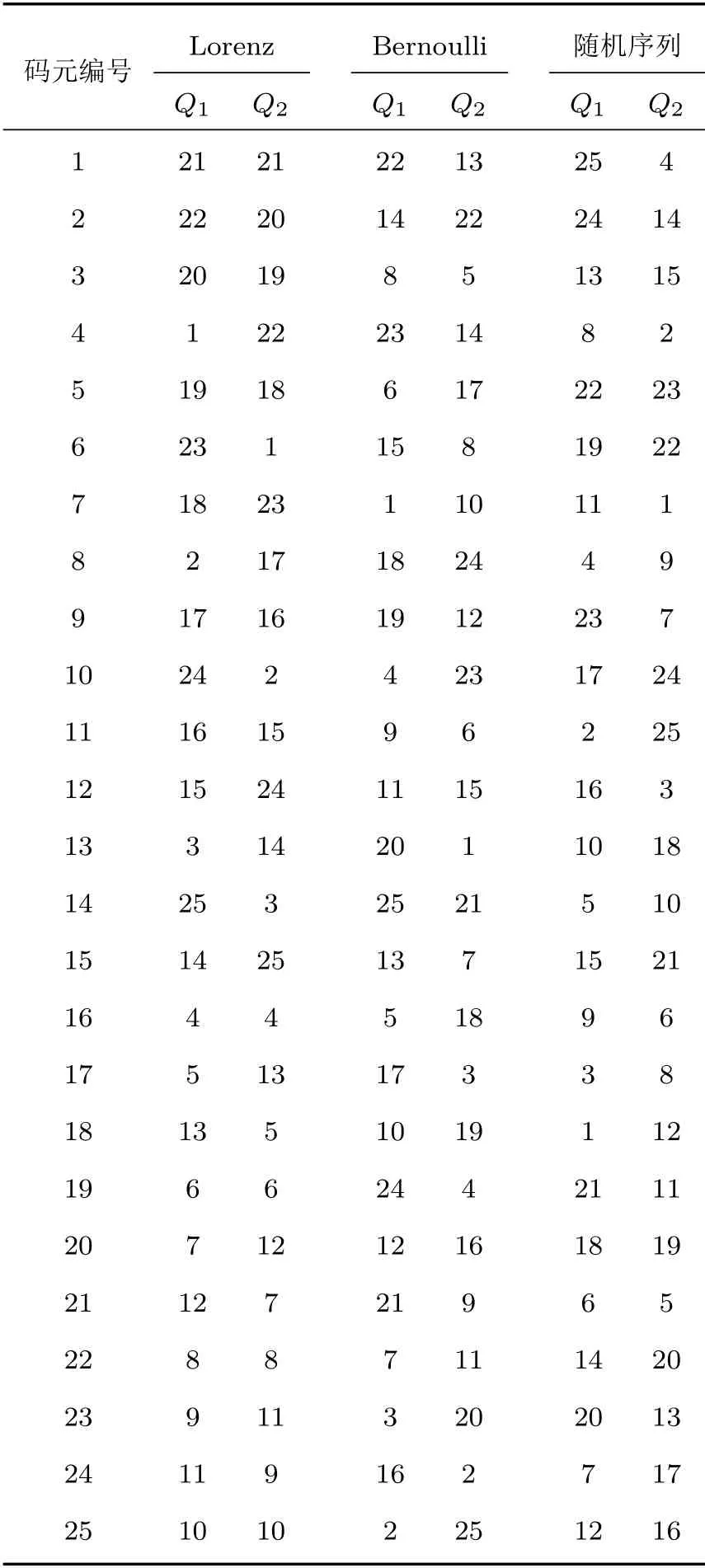
表1 3 種方法生成的編碼序列Table1 Coding sequences of three methods

為了比較本文方法和文獻[16—17]方法設計的離散頻率編碼信號在信號集正交性上的性能，首先定義如下的序列集歸一化最大漢明相關函數：

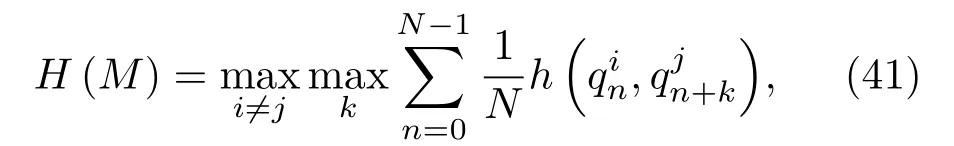
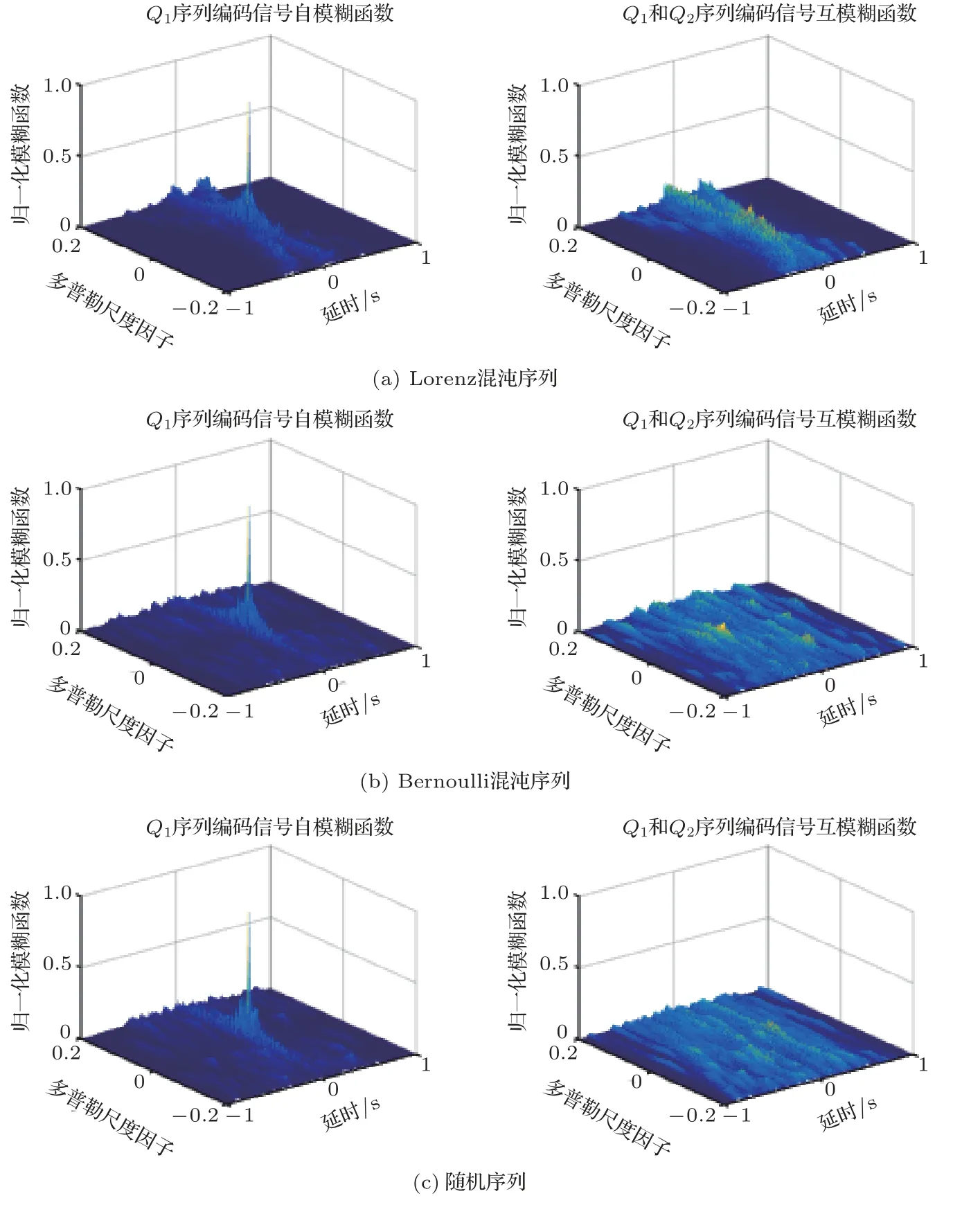
圖6 3 種方法設計信號的模糊函數Fig.6 Ambiguity functions of signals designed by three methods

其中，qin為頻率編碼序列Qi的第n個碼元，為頻率編碼序列Qj的第n+k個碼元，N表示編碼序列長度，M表示序列集中的序列個數，0 ≤i，j≤M -1。函數表示為

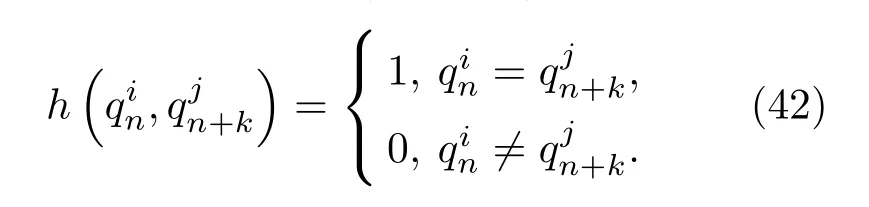
類似的，定義如下的信號集歸一化最大時延相關函數：

其中，函數Rij(τ)為信號si(t)和信號sj(t)的歸一化時延互相關函數，si(t)表示序列Qi編碼的信號，sj(t)表示序列Qj編碼的信號，M表示信號集中的信號個數，0 ≤i，j≤M -1。

設定編碼序列長度為50，信號采樣率為10 kHz，信號時長為1 s，帶寬為1 kHz，信號載頻為500 Hz，生成的序列個數或信號個數M從2 變化到50，進行100 次蒙特卡洛仿真取平均，式(40)、式(42)定義的序列集歸一化最大漢明相關函數和信號集歸一化最大相關函數的變化曲線如圖8所示。對比3種方法的變化曲線可以看出，基于隨機序列生成的序列集和信號集的最大相關函數值更小，基于Bernoulli 混沌的方法次之，基于Lorenz 混沌序列的方法生成的信號彼此間相關性較強。另外，最大的相關函數值隨著信號集中信號數量的增加而逐漸變大，這與理論定性分析的結果一致。對比序列集歸一化最大漢明相關函數和信號集歸一化最大相關函數的變化曲線圖還可以看出，兩種曲線的變化規律一致，即序列集的正交性決定了信號集的正交性，這與3.3 節的正交性分析結果也是一致的。

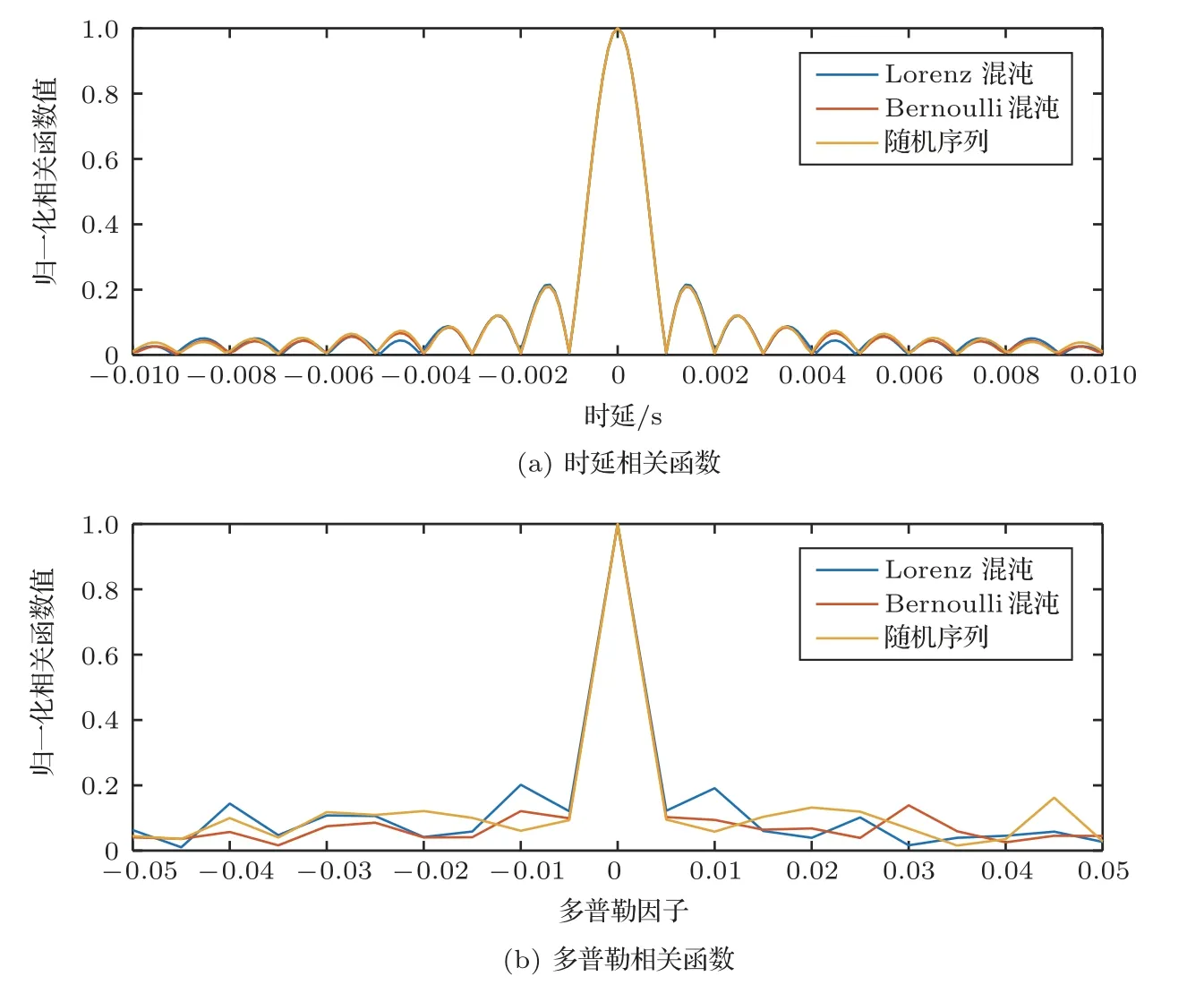
圖7 3 種方法設計信號的時延相關函數和多普勒相關函數對比圖Fig.7 The comparison of three methods on delay correlation and Doppler correlation of signals

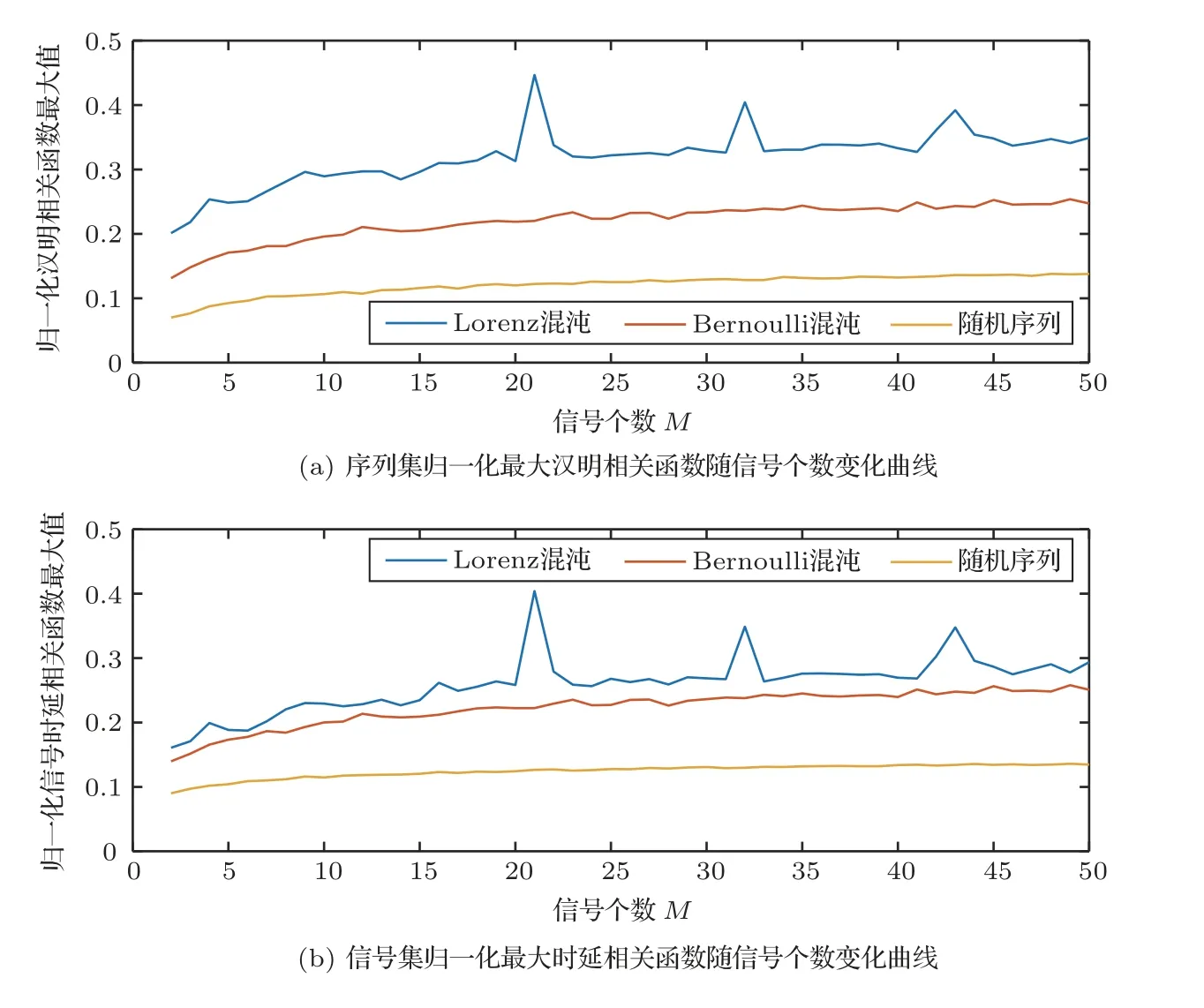
圖8 序列漢明相關函數最大值與信號時延相關函數最大值隨信號個數變化Fig.8 The changing of the maximum of Hamming correlation and the maximum of delay correlation

5 結論

與混沌序列相比，線性同余隨機序列具有更強的隨機性。本文基于線性同余隨機序列設計離散頻率編碼信號，并與文獻[16—17]提出的基于Lorenz混沌序列和基于Bernoulli 混沌序列設計離散頻率編碼信號的方法進行了比較。從理論上推導了離散頻率編碼信號的模糊函數，并分析得出離散頻率編碼信號的時延測量精度取決于信號帶寬，多普勒測量精度取決于信號時長。對基于隨機序列編碼的離散頻率編碼信號的正交性從理論上進行了定性分析，得出不同信號彼此間的正交性主要取決于信號編碼序列的碼元重疊數量，基于隨機序列編碼的離散頻率編碼信號能取得較好的正交性，并通過仿真實驗對這一結論進行了對比驗證。