基于多基因遺傳規劃的儲層巖石靜態模量預測*

王文文 李 諾 韓建強 羅 濤 肖 濤

(1 中海油田服務股份有限公司油田技術事業部 北京 101149)

(2 中國科學院大學 北京 100049)

(3 北京市海洋深部鉆探測量工程技術中心 北京 100190)

(4 中國電子科技集團公司第三研究所 北京 100015)

(5 中國石油渤海鉆探工程有限公司工程技術研究院 任丘 062550)

0 引言

掌握巖石的力學性質有助于解決眾多地球科學、巖土工程等領域的問題，特別是在石油和天然氣的勘探和開發領域。楊氏模量是最常見的力學參數，這些參數可以從巖石壓縮測試(也稱靜態測量)中測量的應力-應變關系中獲得。但是靜態測量實驗裝置復雜，對人員的操作要求高，其過程通常十分耗時而且測試費用昂貴，因此在井中的整個深度區間實施連續取心以獲得巖石力學參數的連續剖面是不現實的，但該剖面在分析井壁穩定性、出砂、壓裂等方面至關重要[1]。實驗室彈性波速度的動態測試相對來說十分高效，而且成本很低，一般利用超聲波脈沖傳輸法測量縱波和橫波速度來計算動態彈性性質[2]。在現場，也可以利用地震勘探或聲波測井得到的地震波或聲波速度來獲得深度連續的動態彈性剖面[3]。

由于儲層巖石復雜的孔隙結構，并且孔隙空間通常含有流體，其動態和靜態性質之間往往存在很大差異[4]。通常對實驗室測量的少量巖心的動靜態數據進行統計分析，利用擬合方法(一般是線性擬合)得到二者的經驗關系，以此對現場的動態數據進行校正來得到靜態性質[5]。然而，由于信號衰減較大，計算巖石動態性質的必要參數——橫波速度在實驗室中往往難以測量；而在測井中，由于聲波測井方法和地層性質的限制，橫波速度也難以獲得[6-7]。這些限制使得動態、靜態性質的轉換問題更加復雜。此外，在回歸建模中，需要用有限的參數和方程預定義經驗模型的結構，現有的經驗關系存在精度較低、適用性不高的問題。為了克服這些局限性，提出一種高精度的方法，從有限的測量數據中預測巖石靜態性質。

近年來，人工神經網絡、模糊推理系統等人工智能方法已經用于解決此類問題[8]，但是它們僅適用大數據集，同時不能提供靜態性質預測的解析表達式[9-10]。本文提出一種基于多基因遺傳規劃(Multi-gene genetic programming，MGGP)的儲層巖石靜態性質預測方法，可以不需要先驗信息建立預測方程。首先，介紹了動態和靜態模量的定義及其區別的內在原因。其次，描述了MGGP算法的特點和流程。最后，通過一組實驗數據分別研究了線性擬合和MGGP 在靜態模量計算中的應用。

1 靜態和動態楊氏模量

靜態楊氏模量是從單軸壓縮測試中獲得的應力-應變曲線直線段的斜率，所謂單軸壓測試，指的是圓柱形樣品在無側向圍壓下承受端部平面上的力。值得注意的是，由于巖石具有非均質、非線性的特點，其應力-應變曲線并不是一條直線，由此可按照斜率的不同定義3 種模量：切線模量、割線模量和平均模量。本文討論的是平均模量及應力-應變曲線近似直線段的斜率，在此段微裂隙完全閉合，可以認為巖石發生的是線彈性變形。此時靜態楊氏模量Esta定義為軸向應力增量Δσz與軸向應變Δεz的比值：

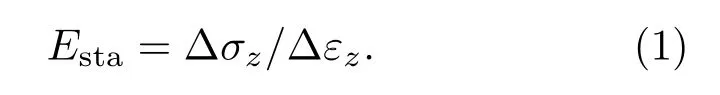
實驗室通常采用超聲脈沖透射法測量樣品的縱橫波速度，根據彈性波傳播理論，動態楊氏模量Edyn定義如下：

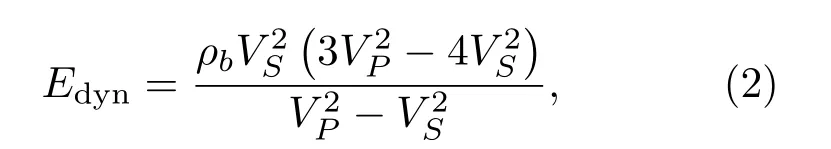
其中，ρb是體密度，VP和VS分別為縱橫波速度。

儲層巖石由于具有復雜的孔隙結構，靜態加載過程中應力加載速率較慢，可以近似為0 頻，變形幅度較大(＞10-4)，變形包括彈性和非彈性成分[11]。而在動態測量中，由于頻率較高，巖石只承受瞬時應力，而且變形幅度很小(＜10-6)，測量過程中的變形可以看作是彈性的。如果巖石飽和流體，由于作用頻率的差異導致靜態測量過程中孔隙壓力處處平衡，動態測量過程中巖石處于不排水狀態，孔壓不平衡，情況更加復雜[12-13]。因此，無論是實驗室超聲透射法還是現場聲波測井方法，得到的動態模量都與巖石的靜態模量都會有差異，甚至差異較大。

2 多基因遺傳規劃

遺傳規劃(Genetic programming，GP)是由Koza[14]提出的一種進化算法。與遺傳算法(Genetic algorithm，GA)類似，GP 以達爾文進化論為基礎，借鑒了生物界的自然選擇和遺傳機制。在一個由多個個體組成的群體中，每個個體都代表一個可行的解，通過選擇、復制、交換、變異等遺傳操作，根據最優適應度逐步迭代，得到最優解。然而不同于只能對字符串進行操作的GA，GP是一種符號回歸方法，可以對樹狀結構的計算機程序進行操作，將輸入與輸出以解析方程的形式聯系起來。多基因遺傳規劃(MGGP)是GP 的變體，結合了GP 的模型構建能力和統計回歸方法的參數估計能力[15]。在傳統的遺傳規劃中，進化模型由一棵樹組成，而在多基因遺傳規劃中，每一個回歸模型都是多棵樹的加權線性組合。利用MGGP 進化得到的模型結構示例如圖1所示，函數集和符號集分別構成樹的節點和葉。在圖1中，函數集包括“log，+，×，sin”，終止符集包括“A，x1，x2”，d0是偏置項，d1和d2是權重系數。與GP 相比，MGGP 能夠使預測模型具備非線性特征，從而具有更高的精度和效率[15-16]。

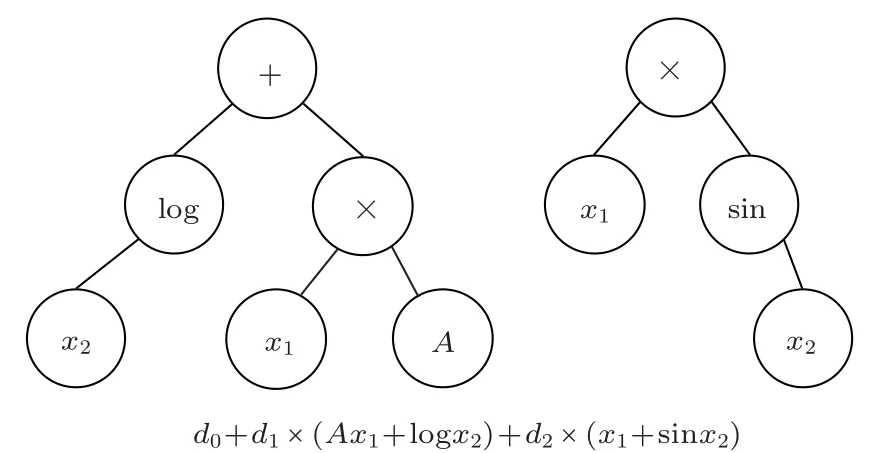
圖1 利用MGGP 進化的一種典型模型結構Fig.1 A typical structure of model evolved by MGGP

圖2給出了MGGP的工作流程，可以概括如下：

(1)隨機產生初代種群，包含一組由函數和變量組成的個體；

(2)計算種群中每個個體的適應度；

(3)選擇適應度好的優良個體為母體；

(4)通過突變、交叉、復制等方式產生新的個體，創造新的一代(子代)；

(5)重復步驟(2)和步驟(3)，直到滿足終止準則。

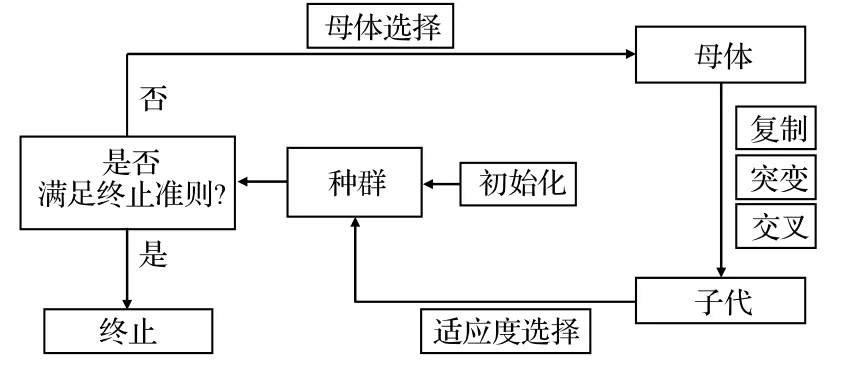
圖2 MGGP 算法的一般流程Fig.2 The general workflow of MGGP algorithm

用于評估模型的適應度函數是實際值ydata和預測值ypre之間的均方根誤差(Root mean square error，RMSE)：

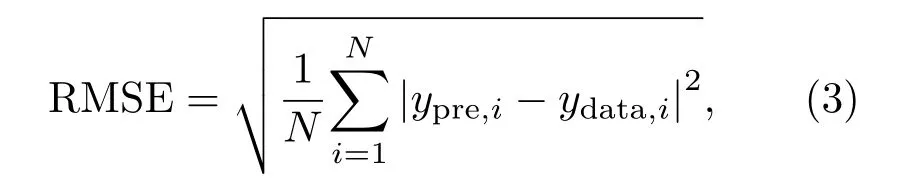
其中，N為參與評估的樣本數目。用相關系數R來表示測量值與預測值之間的相關關系密切程度，即兩個變量之間的協方差和兩者標準差乘積的比值。

3 實驗測量與結果

實驗中，共對32 塊井下取心的砂巖樣品進行實驗測量與分析，相關實驗在中國科學院聲學研究所的高溫高壓巖石動靜態三軸實驗系統GCTS RTR-2000 進行，如圖3所示。該裝置包括主鋼架、壓力控制器、超聲波控制器等，能滿足樣品干燥和飽和態下的聲學和力學參數測量。該系統最大作用力2000 kN，內置精度為0.15%的載荷傳感器，能夠進行軸向應力加載；儀器配置有圍壓孔壓加載裝置，最大加載量140 MPa，精度為0.25%，可以進行圍壓加載；實驗中軸向應變加載速率為每秒0.001%，一分鐘測量一次；采用量程±3 mm的線性可變差動變壓器(Linear variable differential transformer，LVDT)變形傳感器測量應變，精度為0.25%。靜態楊氏模量Esta是應力-應變曲線在30 MPa～35 MPa的應力區間段內的擬合直線斜率，因為在該應力區間內曲線近似為一條直線，可認為巖石發生線彈性變形，見圖4。采用超聲脈沖透射法測量了相同應力范圍內的縱波速度VP和橫波速度VS，結果取為整數，單位為m/s。

圖3 GCTS RTR-2000 巖石力學三軸測試系統Fig.3 The GCTS RTR-2000 rock mechanic triaxial test system

圖4 一塊巖心樣品的單軸應力-應變曲線Fig.4 Stressstrain curve of a core sample

用作為完全彈性體的標準鋁樣進行測試，得到系統測量誤差如下：(1)應力應變測量誤差為0.25%；(2)縱波速度測量誤差為0.52%，橫波速度測量誤差為0.77%；(3)動態模量測試誤差為1%，靜態模量測試誤差為0.5%。

結合測量的體密度ρb，用式(2)計算動態楊氏模量Edyn，結果保留小數點后兩位，單位為GPa。通過SCMS-C3 型覆壓孔滲測量儀測得樣品孔隙度φ，結果保留小數點后四位。所有測量結果在表1中給出，前30塊樣品為飽和測量結果(-S表示)，后30 塊樣品為干燥測量結果(-D表示)。由于測量過程中信號的強衰減，其中4 塊飽和樣品和1 塊干燥樣品的橫波信號由于信噪比較低，沒有獲得可靠的測量值。而且樣品31 和32 在干燥測量后，樣品出現明顯裂隙，沒有進行飽和測量。

表1 樣品參數測量結果Table1 Parameters measurement results of samples

繪制干燥和飽和條件下的動靜態模量交會圖如圖5所示。動態楊氏模量Edyn和靜態楊氏模量Esta之間存在較好的線性相關性，通過線性擬合得到二者之間的線性關系：

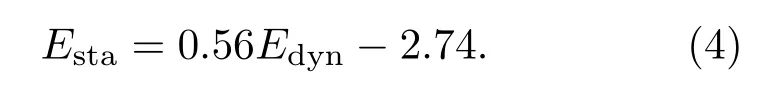
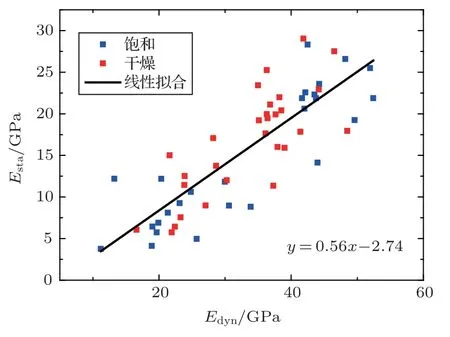
圖5 干燥和飽和樣品的動靜態模量Fig.5 Dynamic Young’s modulus compared to static Young’s modulus of dry and saturated rocks

4 MGGP預測

在MGGP 方法中，靜態楊氏模量為待預測參數，而終止符集中的體密度、孔隙度和縱波速度是預測參數，函數集包含運算符“+、-、*、/、sqrt、ln(x)、log(x)、exp(x)、abs(x)、square、cubic、power、sinh(x)、cosh(x)、sin(x)、cos(x)”。終止符集和函數集用來構建MGGP 模型。隨機選取70%的數據進行模型的訓練，其余30%的數據進行測試。表2列出了構建楊氏模預測模型所用的MGGP 模型參數。

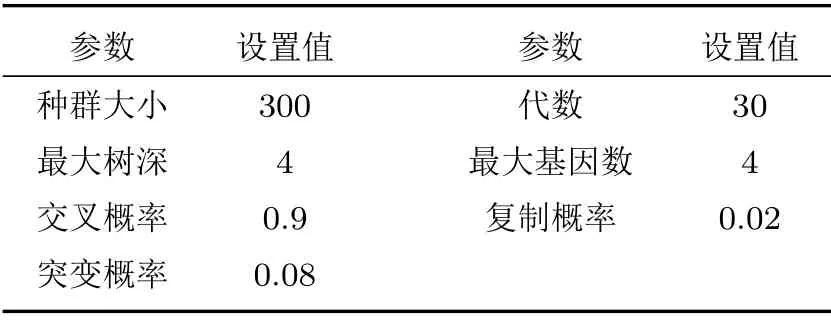
表2 預測靜態楊氏模量的MGGP 模型參數Table2 MGGP model parameters used to predict static Young’s modulus

在進化300 代之后適應度函數均方根誤差RMSE 值為3.44，得到了一個關于孔隙度φ、體密度ρb和縱波速度VP的靜態楊氏模量方程：

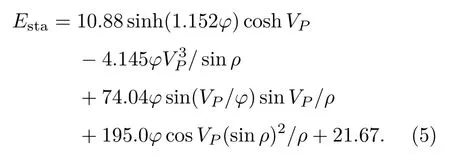
為了驗證式(5)的效果和適用性，將MGGP 預測的結果和動態數據標定值(式(4))分別與實際測量值進行了比較，結果如圖6和圖7所示。在訓練集和測試集中，MGGP 模型都能有效地預測楊氏模量，訓練集的相關系數為0.865，測試集的相關系數為0.726。對于線性擬合方程預測結果，5 塊樣品由于橫波速度缺失而缺少經驗預測值(在圖中顯示為0 值)。除去缺少數據的5 塊樣品，線性擬合結果與測量值的相關系數為0.829。由此可見，與利用動態數據得到的線性模型相比，MGGP 訓練集中預測的楊氏模量更接近實測靜態值，并且對于測試集也有很高的精度，同時避免了橫波數據缺失無法直接計算的影響。

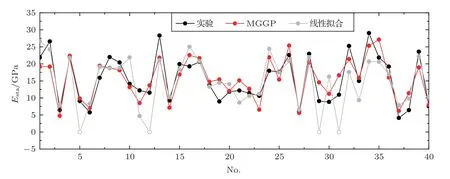
圖6 訓練集線性擬合、MGGP 模型靜態楊氏模量預測值與實驗測量值對比Fig.6 Static Young’s moduli from experiment，linear fit and MGGP in training set

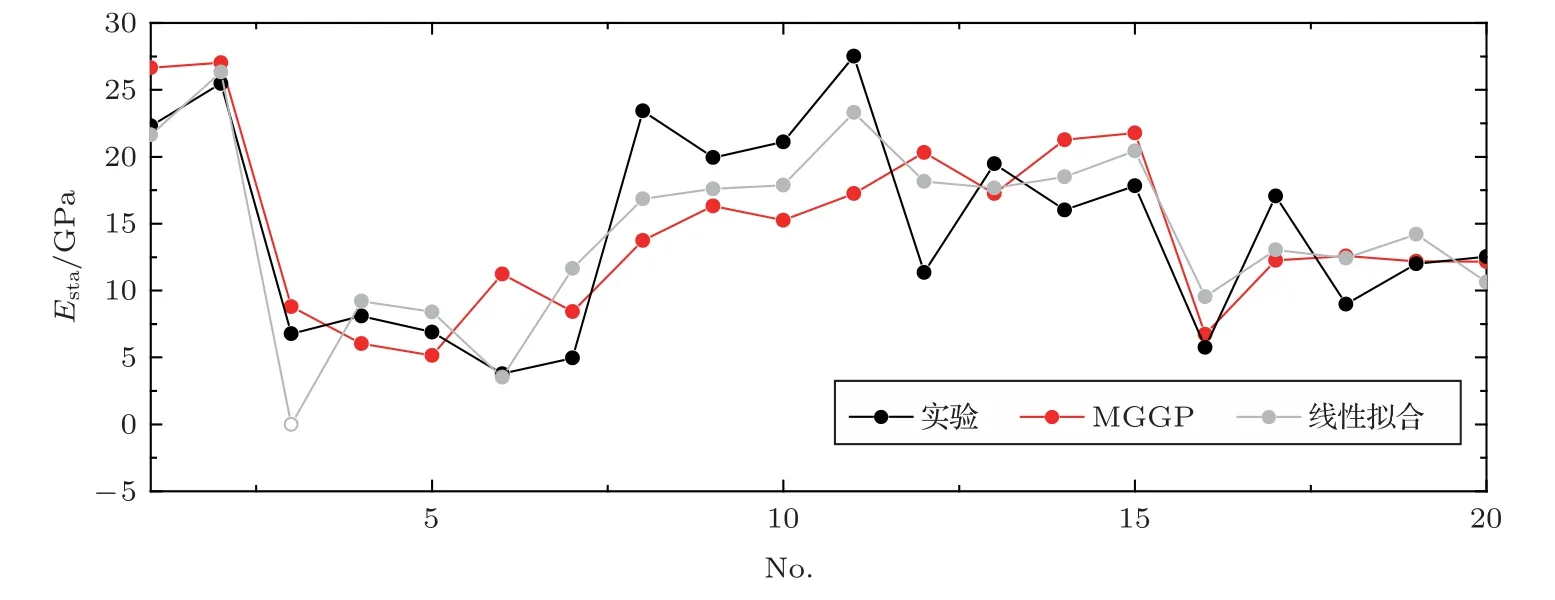
圖7 測試集線性擬合、MGGP 模型靜態楊氏模量預測值與實驗測量值對比Fig.7 Static Young’s moduli from experiment，linear fit and MGGP in testing set

5 結論

本文采用MGGP 方法對儲層砂巖樣品的靜態楊氏模量進行了預測。該模型比用動態數據線性擬合標定的經驗關系有更好的適應性。此外，在缺失橫波速度的情況下，它也能夠利用較少的輸入參數，即孔隙度、體積密度和縱波速度來進行預測，從而減小了橫波波速度不準確或丟失所引起的計算誤差。結果表明，MGGP 在實驗中用來預測靜態楊氏模量是可行的，這為現場數據(測井或地震)在解決巖石力學問題提供了更好的數據處理手段。