一道數學例題的多種解法及教學啟示
朱敏敏

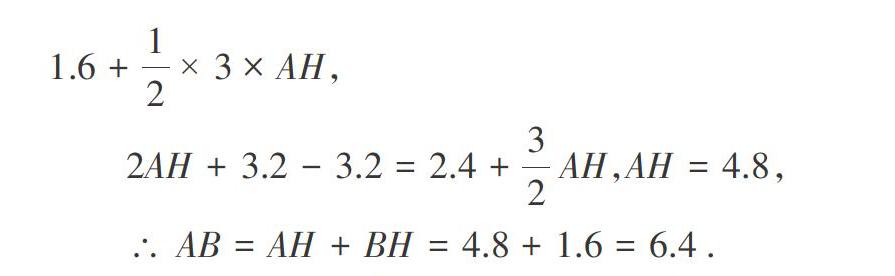
[摘要]數學課堂離不開解題,解題是思維的書面載體.數學例題的教學既能很好地檢驗學生基礎能力和基本技能,又有助于學生領悟數學思想方法,形成數學經驗,從而提升學生的綜合素質和思維品質充分挖掘數學例題的價值,可以促進學生數學智慧的發展和數學素養的提升
[關鍵詞]例題;解法;思維;啟示
[中圖分類號]
G633.6
[文獻標識碼] A
[文章編號] 1674-6058(2020)17-0016-02
數學課堂離不開解題,正如數學家波利亞所言“掌握數學就是意味著解題”.解題是思維的書面載體,“會解題,解對題”是解題的真諦.教師在教學中要加強對解題方法和解題思想的研究,加強對學生思維能力的訓練,提升學生的數學核心素養.教材中的例題集中體現了專家們的智慧.例題的教學既能很好地檢驗學生的基礎知識和基本技能,又有助于學生領悟數學思想方法,形成數學經驗,從而提升學生的綜合素質和思維品質.如何充分挖掘數學例題的價值,實現數學教學的日標?下面筆者以新蘇科版教材的一道例題的多種解法,談談自己的教學啟示.
[例題]如圖l,河對岸有一燈桿AB,在燈光下,小麗在點D處測得自己的影長DF=3m.沿BD的方向前進到點F處,測得自己的影長4m,設小麗的身高為1.6m,求燈桿AB的高度.
解法一:引用教材解答.
作為“用相似三角形解決問題”的例題呈現,這道題多年不變,教材中例題的解答思路是兩次利用相似三角形的對應邊成比例,尋找中間比,從而構建方程,解得答案.這種解法來自于圖形的直觀提示.因為圖中明確存在兩對相似三角形,學生也會自然而然地想到,并將這種解題思路加以應用,嘗試解答,獲得成功.例題是“雙基”訓練的好載體,課堂教學中教師要耐心引導,充分發揮例題的示范引領功能,培養學生分析問題與解決問題的能力.教師對例題的把握還要“登高望遠”.因為沒有任何一道題可以說是完全徹底解決的,總是可以在原有的解法思路上引導學生再審視、再反思,反思題日價值的過程便是好的解法技巧發現的過程.
讓我們重新回到題目中來,引導學生仍然把思維的中心放在“相似三角形的性質”這個知識點上,除例題解法中用到的“相似三角形的對應邊成比例”外,你還能想到相似三角形的哪些性質?學生會得到“相似三角形的對應線段成比例”.
解法二:巧用相似三角形的性質.
這種解法相對于例題解答,變兩次相似為一次相似,簡化了推理過程和計算過程,更利于學生的理解.
解法三:妙用面積法.
“面積法”是解決幾何問題時常用的方法,它的最大優點是可以簡化推理過程,使問題解決的直觀性增強.題日的本身看似與面積無關,巧妙之處在于利用三角形面積的可分性,從兩個不同的角度把△AEF的面積分成兩個三角形的面積和( S△CEF+ S△ACE)與兩個三角形的面積差(S△ACF-S△GEF),建立方程計算求值,使得問題的解決“別出心裁”.整個過程完成了從“形”到“數”的轉化,更利于學生直觀地理解.既培養了學生解決實際問題的能力,又提升了學生應用數學的意識.
《義務教育數學課程標準(2011年版)》對于數學模型有非常明確的說明:數學模型的建立是學生體會和理解數學與外部世界聯系的基本途徑,是學生數學能力的體現.這種用代數的思想解決幾何問題,知識上綜合性強,想法上大膽、開闊,思維上創新力度大.要達到這種層面,對教師和學生都提出了較高的要求.
教師在平時的日常教學中,應竭盡全力引導學生探索一題多解.通過一題多解,引導學生從不同的角度思考問題,找尋各種不同的方法,找尋條件與問題之間的聯系,通過多種不同的路徑達到解決問題的目的.一題多解的探索過程輻射面廣,發散性強.從知識上看,延伸到了數學的各個領域,很好地溝通了知識之間的內在聯系;從解題層面上看,學生調動了各種感官,主動參與,觀察、猜想、交流、反思,具有科學研究的味道;從教學效果上看,有效性向最大化逼近,課堂變得更大、更活、更深,變得引人人勝;從思維上看,從解決試題到反思試題再到欣賞試題,學生的各種思維交織在一起,數學思想方法得到了巧妙地鑲嵌,解題情感得到了升華.在思維小球不停地滾動中,潛能被挖掘,創造欲望被激發,學生終將學到比任何具體的知識更重要的東西.
[參考文獻]
[1]喬治·波利亞怎樣解題[M]北京:科技教育出版社,2011
[2]嚴玲鳳解題:數學課堂的生命力[J]考試與評價,2012(7):25
(責任編輯 黃桂堅)

