調度問題中的算法

陳道蓄

說到“調度”，人們往往會想到交通運輸部門的運行安排，也會想到企業中復雜的生產任務安排。其實，日常生活中也經常面臨著多個事項需要合理安排;只不過任務數不大，也不涉及明顯的經濟指標限制，人們憑經驗就足以應付，很少會聯想到“算法”。當需要解決的任務數增加，且包含相互依賴關系時，算法可以幫助我們順利有效地完成任務。

● 單純依賴關系約束下的任務調度

我們從僅考慮任務間的依賴約束開始。如果任務X只能在另外某個任務Y完成后才能開始，我們就說X依賴Y。下面來看一個簡單的例子。

同學們打算在教室里組織一場聯歡活動，還準備自己動手包餃子。他們擬定了一張準備工作任務表，包含所有任務事項、每項任務耗時、任務間依賴關系（注意：只需列出直接依賴關系，而間接依賴關系自然地隱含在其中）。管理上通常將這些任務的集合稱為一個“項目”。任務列表見表1。

有些任務之間沒有依賴關系，執行順序無關緊要，如果有多個執行者，這樣的任務就可以并行。這里說的“調度”，就是要給每項任務分配一個不同的序號，表示它們執行的順序，滿足：如果任務X依賴任務Y，則X的序號就要大于Y的序號;如果兩個任務之間沒有依賴關系，則對它們的序號關系沒有要求。從數學上看，原來所有任務間的依賴關系確定了一個“偏序”，即并非任意兩個任務都必須“有先后”（稱為“可比”）。調度就是要在此基礎上生成一個“全序”，即任何兩個任務皆“可比”，對任意兩個原來就“可比”的任務，新關系與原關系保持一致。換句話說，如果按照這個序號串行執行，一定滿足原來要求的依賴關系。這個問題被稱為“拓撲排序”問題。讀者應該注意到，如果只要解決拓撲排序問題，我們并不需要考慮上述例子中每項子任務的耗時。

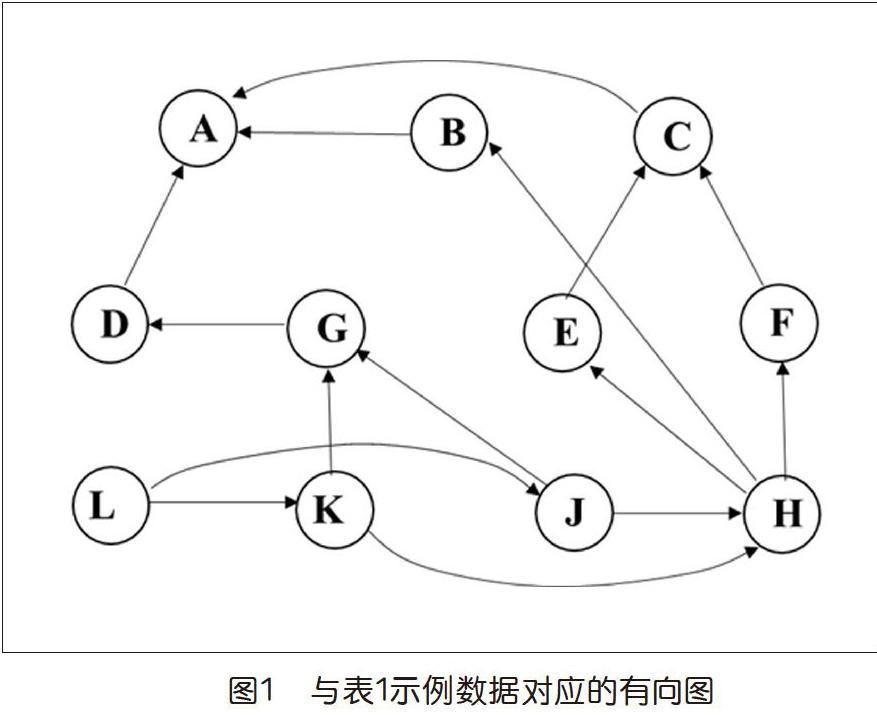
我們可以建立一個有向圖模型。圖中每個節點表示一個任務，節點X和Y之間存在從X到Y的有向邊（X→Y）當且僅當對應的任務X直接依賴于任務Y。上述例子的圖模型如下頁圖1所示。圖中節點名稱采用表1中的任務名稱。我們暫時不考慮任務的耗時。

在這個模型上解決拓撲排序問題的思路非常簡單。我們要給每個節點分配一個序號，這需要遍歷所有節點。根據問題要求，如果任務X依賴任務Y（無論是直接還是間接），分配給節點X的序號必須大于Y的序號。在圖模型中存在的任意一個簡單有向通路v1，v2，…，vk表明任務i-1依賴任務i（1

圖節點遍歷常用算法有兩種：深度優先與廣度優先。我們在本系列文章中前面討論走迷宮算法時介紹過深度優先算法（DFS）。它的基本步驟如下（這里假設從起始點一定可通達所有節點）：①選擇一個起始點，并將其作為第一個“當前節點”，設置狀態為“已訪問”。②如果當前節點所有的相鄰節點都是“已訪問”狀態，結束從當前節點開始的遍歷子過程，退出（回溯）。如果當前節點就是起始點，則整個遍歷完成。③取當前節點相鄰節點中的一個尚未訪問過的節點w作為新的“當前節點”，設置狀態為“已訪問”，從w開始遞歸執行本過程（即上述第2步）。

在圖1中從L開始執行深度優先搜索過程，可能產生的一個訪問序列如下：L，K，H，F，C，A（A，回溯）（C，回溯）（F，回溯）（H），E（E，回溯）（H），B（B，回溯）（H，回溯）（K），G，D（D，回溯）（G，回溯）（K回溯）（L），J（J回溯）（L，結束）。它對應表2中的“訪問序”。具體的訪問序列與當前節點的所有相鄰節點被訪問的次序有關（由算法實現決定，即上述算法第3步節點w的選取）。這對后面生成的全序有影響，但對滿足問題的約束條件沒有影響。

下面來看“拓撲序”的確定。在深度優先搜索過程中，任一節點在回溯后就再也不會被訪問了，也就是它所依賴的節點都已經訪問過了，因此如果我們在其即將回溯前給它分配拓撲序號，且號碼值從1開始依次加1，則上述過程給出的拓撲序號與任務名稱的對應關系如表2中的第三行所示。讀者容易驗證這個次序滿足表1中的任務依賴要求，即按照這個序號，先做“1”（A），后做“2”（C），……，最后做“11”（L），就不會出現當要做一件事的時候，它前面還有該做沒做的事情。

對前述深度優先算法稍加修改（在回溯前給節點編號），即可得一個拓撲排序算法（留作讀者練習）。其中有兩點值得注意：第一，起始節點（將最后編號）應該是不被任何其他節點依賴的，即要選入度為0的節點;第二，對于任意的依賴關系輸入，拓撲排序問題未必都有解。設想一下，有兩個任務X和Y，X依賴于Y，但Y也依賴于X（可能是間接的），這就形成了所謂相互依賴的“死循環”，無論怎么安排都沒法滿足它們。這種狀況在圖1所示的圖模型中體現為一條有向回路。在算法中判斷這種情況的標準方法是用3個狀態（通常形象地用顏色白、灰、黑標記）來表征一個節點在深度優先搜索過程中不同時間段上的情況。White表示“尚未發現”，grey表示“已發現但還未關閉”（在進入DFS時設置），black表示“已關閉”（即已回溯，在離開DFS時設置）。在第2步，發現了一個灰色節點，就意味著圖中存在回路（讀者可想想其中的道理）。

這個算法只是在深度優先搜索過程中增加了常數次簡單賦值操作，所以其時間代價與深度優先搜索算法一樣，為O（m+n），其中m與n分別是輸入圖的邊數與節點數。

對于不熟悉深度優先等遞歸性質算法的讀者，還可以有一個概念上較簡單，但時間代價較大一些的拓撲排序算法。其要點是：不斷刪去有向圖中出度為0的節點。刪除的順序就是節點的拓撲序。這種思路的程序實現十分容易，直接操作鄰接矩陣就可以，不用遞歸，對初學者有一定教益。

● 執行時間與依賴關系共同約束下的任務調度

現在我們來考慮任務執行時間的影響。將表1給出的例子畫出反向依賴圖，并將每個子任務的耗時標注在指向相應節點的邊上，我們就得到圖2。此時，邊A→B的含義是“B必須在A做完了后才可以開始”（即B依賴于A），上面的“30”表示B需要耗時30分鐘。顯然，邊上的數據標在箭頭末端的節點上也是可以的。

這樣一個任務關系圖中顯示了在人力允許的情況下可以并行執行的多條路徑，如在任務A完成后，可以同時執行{任務B}以及{任務C，任務E}，甚至還能同時執行{任務D，任務G}（大括號內的任務串行執行）。圖中粗線顯示，到整個項目執行完成最長的一條路徑是A→C→F→H→J→L（圖中用粗線表示）。這條路徑耗時130分鐘。如果不能壓縮這條路上的耗時，其他任務即使壓縮了耗時也不能將整個項目的完成時間提前。因此，這條路徑稱為“關鍵路徑”，關鍵路徑中體現的依賴關系稱為“關鍵依賴”。在這個例子中，單項任務耗時最多的是包餃子（G，80分鐘）。增加一些人手可以將其耗時降下來。但它并不在關鍵路徑上，因此包餃子提前完成對于整個項目縮短時間并沒有任何意義，只是增加了一些閑著等待的人。

此時，調度的追求是識別關鍵路徑，從而得知完成整個工作所需時間的下界。在任務管理中，找出關鍵路徑，并通過有針對性地加大資源投入、改進技術等手段壓縮該路徑上的耗時，是提高辦事效率的重要方法。

基于前述深度優先搜索算法，適當記錄中間結果，就可以解決這種關鍵路徑問題。它包括兩個方面，一是關鍵路徑的長度（時間），二是路徑本身（經過的節點）。在這個意義上，和上一期討論的“投資組合問題”有共通之處，即不僅要得到一個目標量值，還要得到構成該目標量值的具體實現。這也是計算機問題求解中的一種相當廣泛的要求，策略大都是通過在追求目標量值的過程中記錄某些中間結果，然后通過它們反演出具體實現方案。下面來看怎么解決這個問題。

這里的關鍵是要認識到，如果任務A直接依賴任務B，則A的最早“開始時間”不可能早于B的最早“完成時間”。進而，若A依賴多個任務，則A的“開始時間”不可能早于它們“完成時間”的最晚者。而一個節點的完成時間等于它的開始時間加上它的耗時。

這樣，參照圖2，如果我們確定了每個節點的最早“完成時間”，對應最后一個任務（L）的，就是關鍵路徑的長度。而在L所依賴的節點中，誰的完成時間最晚，也就是關鍵路徑上的前一個節點。如此繼續，直到起始節點A，就反演出了關鍵路徑的構成。鑒于實現這種思路的程序不長，下面我們將基于圖3中的可執行Python函數予以解釋。

其中用到的幾個數據結構是——①neighbor：線性表向量，初化為每個節點的出向鄰居，基于圖1（而不是圖2）的方向性;②delay：向量，輸入數據，記錄每個節點的耗時;③visited：向量，記錄節點在深度優先過程中是否被訪問過，初始化為全False;④finished_time：向量，記錄節點的最早完成時間;⑤critical_dependance：向量，記錄關鍵依賴關系。

看這段程序，如果沒有行2，8～10，14～17，那就是一個從current_node（當前節點）開始的標準深度優先搜索。其中第4行的for語句保證當前節點的每一個依賴關系（x）都會被考慮到。9～10，14～16行就是我們說的記錄中間數據。站在當前節點的角度，把所依賴節點的完成時間的最大者定為自己的開始時間（my_starting_time），同時也在critical_dependance中記下它。最后再加上自己的耗時，得到自己的完成時間，供依賴自己的節點后續參考。

這其中有兩點值得注意，一是為什么要考慮當前節點的所有依賴節點，而不僅是剛看到的white節點？這是因為前面說的，當前節點的最早開始時間不得早于所依賴節點的最晚結束時間，與訪問順序無關。二是在最后的critical_dependence中，不僅記錄了從開始任務到結束任務的關鍵路徑信息，還記錄了從開始任務到任何任務的關鍵路徑信息。基于圖3的程序，運行前面的例子，結果如表3所示。

從中，我們可以反演出整個任務圖的關鍵路徑：A→C→F→H→J→L。

從上述討論中能看出，這個算法只是根據特定問題的需要，在深度優先搜索算法中加入適當代碼保留一些中間數據，就實現了我們期望的問題求解目標。這樣，我們就能夠將DFS過程當作一個“算法框架”，可以用它拓展出針對不同問題的許多算法。

關于關鍵路徑問題的求解，最后需要提請讀者注意的是，它所面對的圖不僅應該是有一個有向無環圖，還應該是有唯一“起始節點”（入度為0）和唯一“結束節點”（出度為0）。每個節點都可達結束節點，都可被起始節點到達。為此，在實際應用中有時需要添加虛擬的起始節點和結束節點，算法方可正確運行。

● 負載均衡調度問題

本文開始就提到調度問題最大的應用背景應該是生產活動，具體應用與限制條件的不同發展出了大量的調度問題，與我們前面的拓撲排序問題有很大差別，生產實踐中產生的調度問題大多屬于“難”問題。對于計算機科學家而言，“難”問題通常指這樣的問題：問題輸入規模增加到足夠大時，我們傾向于相信全世界的計算資源都不足以支撐我們獲得問題的最優解。但調度問題的解往往涉及巨大的經濟效益，這就促使人們設法尋求可接受的解決途徑。放棄對最優解的追求，轉而滿足于質量有一定保證的近似解就是目前遵循的最重要的途徑之一。令人驚喜的是，這往往會帶來非常簡單但可以滿足實踐需要的算法。下面用一個最容易表述的例子來讓讀者形成一些初步的認識。

考慮需要在m臺完全相同的機器上執行n項沒有依賴關系的任務，pi（i=1，2，…，n）為任務i的耗時，在任何一臺機器上執行都一樣。假設每項任務不可分割，如何將n項任務分配給m臺機器，使得項目總執行時間最短？這個問題稱為“（多臺相同機器上的）工期問題”。稍微想一想，不難認識到這里就是要追求讓n個任務盡量“均勻地”（以時間為衡量）在m臺機器上分配，而最優解不可能小于S=∑ipi/m。

顯然，如果機器數m大于等于任務數n，因為任務不可分割，則最大任務耗時就是整個項目最小完成時間。我們下面約定n>m。可以證明工期問題是上面所說的“難”問題。按照最直觀的貪心策略我們就可以找到一個結果“可控”的近似算法。

一個自然的想法是：先把m個最大的任務安排給每臺機器，剩下來的再逐個往不同的機器上“塞”。“塞”的原則很簡單，當前哪臺機器負載最小（即完成已分配任務所需的時間最短）就給它加任務。為此，我們先對所有任務按時間降序排序[時間復雜度為O（nlogn）]，然后一一安排。整個算法過程如圖4所示。其中的關鍵數據包括：①一組集合Ti，1≤i≤m，Ti的元素為已分配給第i臺機器的任務下標，算法終止時輸出Ti;②數組Time：Time[i]的值為第i臺機器當前總負載，算法終止時，Time[i]（i=1，2，…，m）的最大值即為算法計算的結果。

強烈建議讀者用自己熟悉的語言實現這個算法，特別是用盡可能簡單的方法實現其中“找出負載最小的機器”。作為一個例子，假設n=10，m=3，任務的負載為80，40，40，30，30，20，20，10，10，5。按照算法，運行結果如表4所示。

前面我們說這個近似算法是“可控”的，這是什么意思呢？我們希望確定算法的輸出與最優解差距有多大？這似乎提出一個“悖論”：如果我們知道最優解，根本不必費心去找近似解;但如果不知道最優解，怎么能知道差距有多大呢？奧妙在于利用數學知識與算法本身的特性，我們可以試圖估計出差距的“上界”。這個問題是求最小值問題，因此算法輸出的近似解一定大于最優解。如果能確定“最壞情況下”大多少，使用者心中就“有底了”。

這里的關鍵在于能否估計最優解的值的“下界”，即最優解至少得多大。前面已經提到，最優解不可能小于均值S=∑ipi/m，即它就是一個下界。

現在來考慮算法本身的行為。假設整個項目中最遲完成的任務下標為k，則安排任務k時的場景示意如圖5所示。

假定任務k被分配給機器l，則當時機器l是負載最小的，因此Time[l]一定不大于前面k-1個已安排任務的平均耗時。而這只是所有任務中的一部分，所以一定不大于∑ipi/m，因此也不大于最優解。考慮到pk是最小的負載，因此不可能大于平均值（最優解的下界），算法輸出的值，就是這兩項的和，一定不大于最優解的2倍。在表4所示的例子中，總時間為80+40+40+30+30+20+20+10+10+5=285，因而在3臺機器并行條件下，最短時間不會少于285/3=95。剛才的結果是max（100，95，90）=100，相當不錯了。

這種保證得到的解不大于最優解2倍的算法也稱為2-近似算法。至于實際應用場景能否容忍這樣的誤差就得由用戶自己決定了。采用更復雜的技術可以進一步降低工期問題算法的誤差，甚至可以做到“任意小”（當然效率成本會迅速提高）。

參考文獻：

[1]Sara Baase.計算機算法——設計與分析導論（第3版）[M].北京：高等教育出版社，2001.

[2]Juraj Hromkovic.Algorithmics for Hard Problems（2nd ed）[M].Berlin：Springer-Verlag， 2004.

[3]陳道蓄.迷宮問題中的算法[J].中小學教材教學，2019（10）：76-80.

注：作者系南京大學軟件學院原院長，計算機系原系主任。