字母跑馬燈

陳凱

在人工智能的學習過程中，有不少經典的算法需要掌握，如一般要掌握樹結構或圖結構中數據的搜索方法，其中比較基礎的內容，是對樹結構做廣度優先搜索和深度優先搜索。但在實際教學中，卻可能會遇見一個矛盾，若是學校并沒有將“數據結構”模塊與“人工智能初步”模塊一起列入選擇性必修的內容，那么在講解樹結構的搜索問題時，面對學生從未接觸過的“樹”這種數據結構，教師該如何平衡好教學內容的安排呢？

一個辦法是干脆繞過對“樹”這種數據結構實現過程的講解，直接使用現成封裝好的對象，對樹結構進行操作。這樣雖然可以降低教學上的難度，卻難免會有些空中造屋或隔靴搔癢的感覺，并且，由于使用了現成的對象，即便完成了樹結構的遍歷和搜索任務，學生的成就感也不會很充足。所以這里就有了一個值得思考的問題：怎樣尋找替代方案，簡化數據結構和程序代碼，減少教學的容量，與此同時，還要將實現樹結構中的搜索的關鍵思想表現出來，為計算思維的培養提供落實點。本文給出的“字母跑馬燈”教學活動，就是為解決上述問題而做的一個嘗試。

● 樹和字母跑馬燈

先來畫一棵樹，為了清晰簡單，此處的樹的分叉最多為2，并且，樹的節點信息，就是它的名字本身。如圖1所示，若從根節點開始，對這棵樹進行廣度上的遍歷，那么依次訪問的節點應該是：A—B—C—D—E—F—G—H—I—J。訪問節點的名字“恰好”按字母順序排列，這當然是筆者有意安排所致。

可以根據每個節點和它分叉通向的節點建立一張規則表，這樣，即便沒有直觀看到樹結構的展示圖，也可以在拓撲學的意義上，將樹的結構重新還原出來，規則表中，不再繼續分叉的節點，后續的字符串為空（如圖2）。

接下來，就可以玩名叫《字母跑馬燈》的游戲了，首先設初始值，就是先放置樹的根節點，所以可以在紙上寫下只包含一個字母“A”的字符串。然后：第一步，將字符串中的首字母搬運到字符串的末尾;第二步，將字符串末尾的字母，按規則表進行替換;第三步，從第一步開始重復動作。

可以跟蹤觀察一下效果如何，初始時字符串是“A”，第一步是將首字母（就是“A”）搬運到字符串最后，當然，因為字符串中只有一個字母，結果還是“A”，接下來第二步，根據規則表，字符串變化成了“BC”，然后第三步，回到第一步接著進入第二輪變化，第一步進行搬運，字符串變成“CB”，然后第二步，字符串變成“CDE”……每一輪的操作產生的字符串變化過程如下：

A—BC—CDE—DEFG—EFG—FGHI—GHI—HIJ—IJ—J—

可以看出，字符串的首字母就是廣度遍歷時依次訪問的節點名字。實際上，這種運用了“搬運—替換”規則的字符串的迭代過程，是一種被稱為標簽系統（Tag-System）的計算模型。這種計算模型當然不是只能用來模擬樹結構的遍歷，它還能用來實現什么功能，這個問題留給讀者們去思考。

● 將變化過程自動化

可以利用工具，將以上的搬運和迭代過程變成自動化的動作。只要利用文字編輯工具的宏的功能，就可以實現自動化，整個過程中，并不需要輸入任何的程序代碼。

下面，以NotePad++軟件為例來說明宏的制作，此軟件可從網絡上免費下載，也可以使用Microsoft Word、Open Office等辦公軟件來完成類似操作。初始時，在NotePad++的文字編輯區中，寫入“*A”，這里的星號起到替換操作標識的作用。星號后的字母，就是將要執行替換操作的對象。

第一步，創建一個名為“Move”的宏，這個宏的作用是將首字母搬運到字符串末尾。這個宏中包含的操作步驟是：按“Home”鍵將光標移到行首，按“Shift”鍵和右箭頭選中星號和字符串首字母，執行剪切操作，按“End”鍵將光標移到行尾，執行粘貼操作。

第二步，創建一個名為“Replace”的宏，這個宏的作用是按規則表進行替換。這個宏中包含的操作步驟是：依次將“*A”替換成“BC”，將“*B”替換成“DE”，將“*C”替換成“FG”，以此類推。當規則表全部應用完畢后，還要按“Home”鍵，將光標移到行首，并補充一個星號，重新設置好替換標識。

這樣一來，只要反復執行“Move”和“Replace”這兩個宏，就可以實現樹結構的廣度優先遍歷了。下面回顧一下解決遍歷問題的思路：先是將形象的樹的結構抽象成替換規則的編碼，然后用標簽系統這種計算模型來實施符號的搬運和替換，最后再利用文字編輯軟件的宏，來實現符號的搬運和替換的自動化。這些都與計算思維的培養目標相契合。

● 極其簡單的廣度優先搜索代碼

在熟練掌握符號替換的宏的制作后，將廣度優先遍歷的過程轉而用程序代碼實現，就非常容易了。在實際的人工智能教學安排中，對于低年級的學生，可以考慮僅利用宏來進行操作實驗，而高年級的學生，或有算法和程序設計基礎的學生，就可以更上一層樓，借鑒用標簽系統這種計算模型實現樹結構遍歷的方法，編寫出廣度優先搜索的代碼。

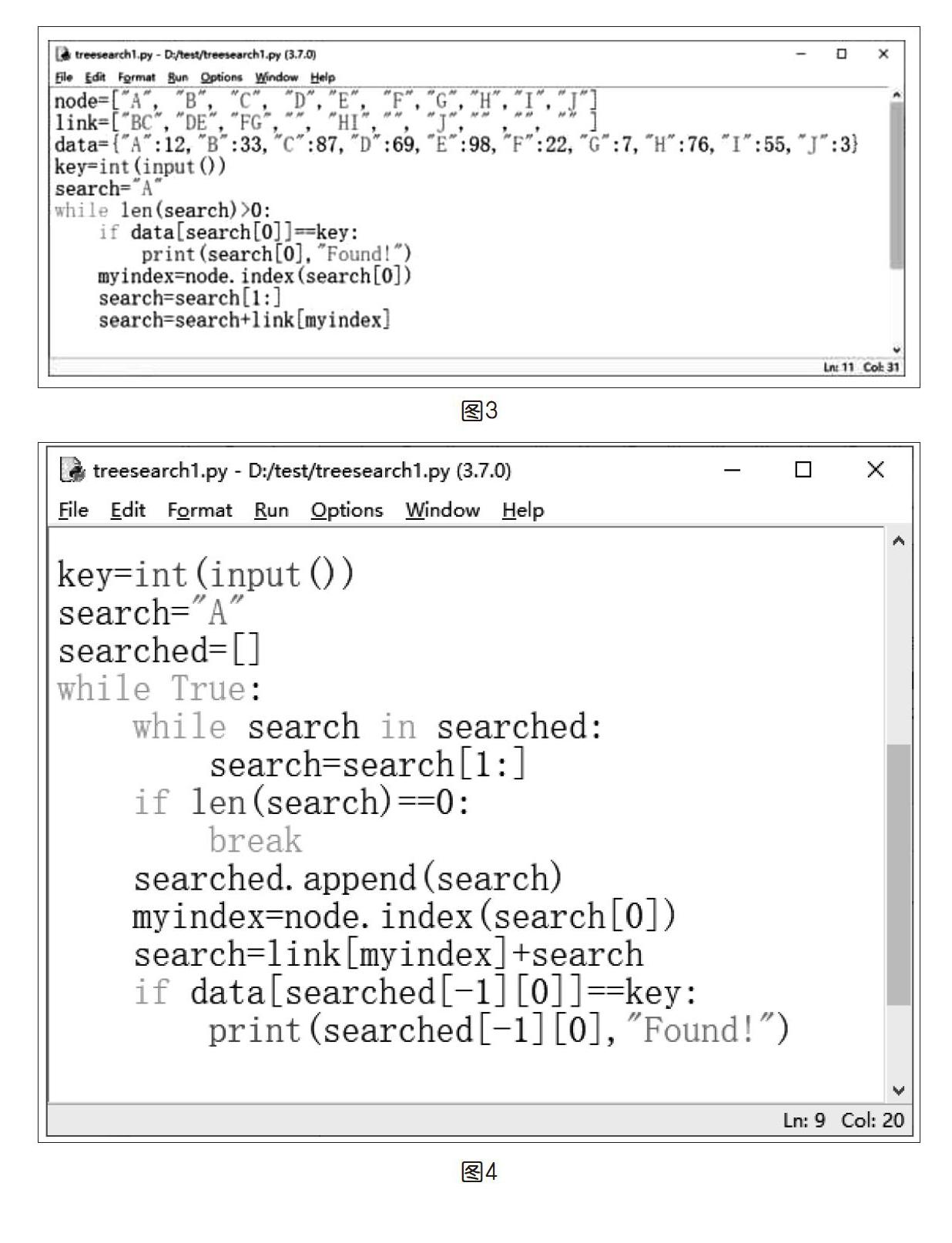
這里提供了用Python代碼實現的例子，代碼中，node列表存儲的是樹的節點的名稱，link列表存儲的是樹的每一個節點分叉的后續節點的名稱，data是一個字典，其中存儲的是樹中每一個節點中存儲的數據信息。search=search[1：]和search=search+link[myindex]兩句語句實現了符號的搬運和替換。代碼可以說是極其簡單了，如下頁圖3所示。

● 相當簡單的深度優先搜索代碼

將上面的方法稍微改一下，就可以實現深度優先搜索了，還是可以試著在Notepad++里玩符號替換的游戲，假設初始的字符串還是“*A”，這一次不需要搬運了，只要對字符串最前面的字母進行替換即可，步驟如下：

第一步，根據樹結構連接的規律，將“*A”替換成“BCA”（其實是將“*A”替換成“BC”后再加上“A”自己），將“*B”替換成“DEB”，將“*C”替換成“FGC”，將“*D”替換成“D”（其實是將“*D”替換成空字符串再加上“D”自己），以此類推。將以上步驟包裝成宏。這種替換字符串的方法稱為馬爾科夫重寫系統，是另一種十分有用的計算模型。

第二步，按“Home”鍵回到行首，補充一個星號。因為只有簡單的一個動作，即便不包裝成宏也是可以的。

然后只要反復執行以上兩步，大致就可以實現深度優先的遍歷了，但在實際操作中，會遇見字符串變化陷入停滯或重復模式的問題。比如，“*A”變成“*BCA”，再變成“*DEBCA”，由于字符“D”對應的是空字符串，于是經過一輪變化后，字符串還是“*DEBCA”。

解決的方法是要加入一點人工干預，當發現字符串的變化陷入停滯或重復的模式中時，就手動刪除行首的字母，若刪除行首字母后仍然陷入停滯或重復的模式，則繼續刪除行首字母。雖然這樣做會顯得整個過程不特別自動化，但也意外地帶來了思考的樂趣：若將要探索的樹比較龐大，那么，是不是應該刪除行首字母？應該什么時候刪除行首字母？這就需要考驗記憶和判斷能力了。若稍微改一下游戲規則，如在規則表中特意放置一個小寫字母，那就可以在Notepad++中玩迷宮尋寶（尋找小寫字母）的游戲了。

如果是借助程序代碼，判定字符串變化是否陷入停滯或重復的模式就十分簡單了，只要將每次字符串的變化情況存入列表，然后在新的一輪字符串變化后，檢查其是否與列表中已有的字符串重復，就可以達到目的了。按這樣的思路，可以將半自動深度優先遍歷的過程，轉換為完全自動的深度優先搜索的程序代碼（如圖5）。

代碼中，searched列表用來存儲每一次字符串變化后的情況，一旦發現有重復模式出現，就用search=search[1：]去除字符串的首字母。整個程序代碼居然只有十幾行，這個結合了深度優先搜索和計算模型的算法，是否簡單到令人震驚？看了本文的例子后，相信老師們對上好廣度優先搜索和深度優先搜索的課，會有更大的把握了吧！

其實，即便是這樣簡單的程序代碼，也還有進一步簡化的可能性，大家有沒有想到，實際上，對于字符串變化有沒有陷入重復和停滯這一步的判斷，并不是必須的！換言之，只要稍微更改一下規則表的使用方法，就可以在Notepad++中實現完全自動化的深度優先遍歷，而程序代碼也可以相應地大幅縮短，到底如何操作？這個問題就留給讀者自己思考吧！