基于遺傳算法多約束條件下的供應(yīng)商選擇研究
韓雪山
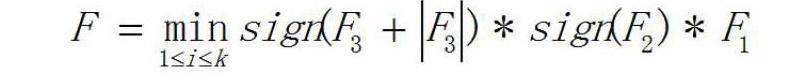

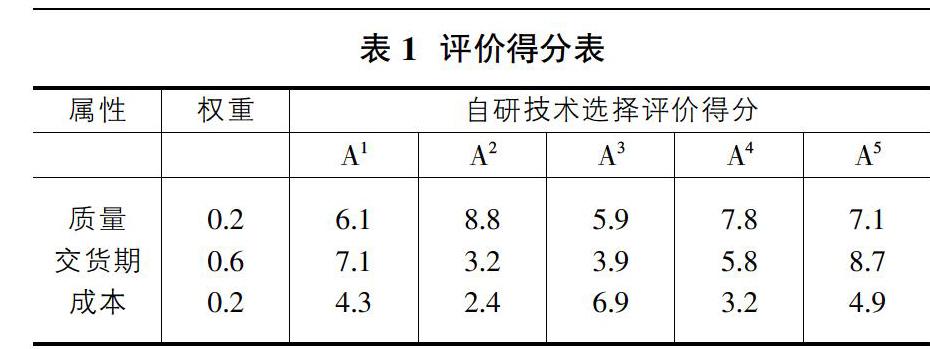
摘要:本文基于遺傳算法,通過(guò)對(duì)適應(yīng)度函數(shù)的設(shè)計(jì),提出了一種新的改進(jìn)的遺傳算法,用于解決從N個(gè)候選方案中選擇M(1 Abstract: Based on the genetic algorithm with the design of fitness function, this paper proposes a new improved genetic algorithm to address the problem of select M (1 關(guān)鍵詞:遺傳算法;組合優(yōu)化;多約束;適應(yīng)度函數(shù);供應(yīng)商選擇 Key words: genetic algorithm;combined optimization;multiple constraints;fitness function;supplier selection 中圖分類號(hào):F274? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻(xiàn)標(biāo)識(shí)碼:A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號(hào):1006-4311(2020)14-0123-02 0? 引言 從理論上來(lái)講,針對(duì)解空間有限而數(shù)量特別巨大的組合優(yōu)化問(wèn)題,可以通過(guò)枚舉法得出優(yōu)化解,但實(shí)際上卻是非常的麻煩。遺傳算法具有全局的搜索能力,與傳統(tǒng)的枚舉法相比,具有很快的收斂速度的優(yōu)勢(shì),因而許多學(xué)者將遺傳算法引入到組合優(yōu)化問(wèn)題中。但是針對(duì)具有多個(gè)約束條件限制下的從N個(gè)候選方案中選擇M個(gè)的最優(yōu)組合問(wèn)題,通過(guò)設(shè)計(jì)相應(yīng)的適應(yīng)度函數(shù)來(lái)求解的文獻(xiàn)卻很少。 本文據(jù)此基于遺傳算法,通過(guò)對(duì)遺傳算法中編碼和適應(yīng)度函數(shù)的設(shè)計(jì),提出了一種新的改進(jìn)的遺傳算法,并將其應(yīng)用到供應(yīng)商選擇的案例中,具有很強(qiáng)的現(xiàn)實(shí)意義。 1? 改進(jìn)的遺傳算法 1.1 遺傳算子的設(shè)計(jì) 編碼。本文采用實(shí)數(shù)編碼,將個(gè)體的每個(gè)基因值用某一范圍內(nèi)的一個(gè)實(shí)數(shù)來(lái)表示,個(gè)體的編碼長(zhǎng)度就等于變量的個(gè)數(shù)。 適應(yīng)度函數(shù)的構(gòu)造。本文采用變化的適應(yīng)度函數(shù)的方案,將問(wèn)題的約束以動(dòng)態(tài)方式合并到適應(yīng)度函數(shù)中,形成一個(gè)具有變化的帶懲罰項(xiàng)的適應(yīng)度函數(shù)。 選擇。本文采用精英保留錦標(biāo)賽選擇。 重復(fù)選擇、交叉、變異的過(guò)程,逐步迭代,直到取得最優(yōu)解時(shí)停止。 1.2 適應(yīng)度函數(shù) 關(guān)于約束條件的限制,我們主要是通過(guò)適應(yīng)度函數(shù)來(lái)進(jìn)行篩選。在進(jìn)行適應(yīng)度函數(shù)的設(shè)計(jì)時(shí),重點(diǎn)考慮以下幾種約束條件:①如果不符合約束條件,則賦予適應(yīng)度函數(shù)較小的數(shù)值;②如果在交叉過(guò)程中,出現(xiàn)了相同的基因,則適應(yīng)度函數(shù)值約束為0;③如果選定一個(gè)組合后,該組合在某一個(gè)指標(biāo)上都很弱,則予以將其剔除。 2? 供應(yīng)商選擇的實(shí)例分析 本文以從5個(gè)供應(yīng)商中選擇3個(gè)的最優(yōu)組合為案例進(jìn)行實(shí)證分析。專家經(jīng)過(guò)討論得出了評(píng)價(jià)供應(yīng)商的三個(gè)重要指標(biāo):質(zhì)量、交貨期、成本。指標(biāo)權(quán)重的確定采用AHP方法得出。從表1中可以得出供應(yīng)商5在交貨期的得分很高,但其在質(zhì)量和成本方面的得分比較弱。供應(yīng)商2在質(zhì)量屬性上的得分較高,而其在成本和交貨期方面得分較低。所以在選擇供應(yīng)商時(shí)具有以下的幾個(gè)約束條件的限制:供應(yīng)商合作伙伴整體最優(yōu),同時(shí)能夠達(dá)到一種優(yōu)勢(shì)互補(bǔ)的效果;如果某一個(gè)供應(yīng)商在某一個(gè)指標(biāo)上的得分很低,則賦予其懲罰約束;如果M個(gè)供應(yīng)商在某一個(gè)指標(biāo)上都很弱,則不予選擇這個(gè)組合。評(píng)價(jià)得分表如表1所示。 接下來(lái),分別采用線性加權(quán)法(方法一)、?姿截集標(biāo)準(zhǔn)化矩陣法(方法二)和本文提出的改進(jìn)的遺傳算法(方法三)進(jìn)行計(jì)算。其綜合結(jié)果如表2所示。 針對(duì)本文提出的改進(jìn)的遺傳算法,其相關(guān)遺傳算子的設(shè)計(jì)為:初始種群為20,交叉的概率為0.6,變異的概率為0.01,終止迭代的次數(shù)為1000。L的取值為L(zhǎng)=(6,5,4.3)T。 三種計(jì)算的結(jié)果并不完全一致。通過(guò)分析,進(jìn)一步得出: 方法一屬于簡(jiǎn)單的線性加權(quán),并未考慮到約束條件的限制,是理想狀態(tài)。該方法適用于從眾多的方案中選擇一個(gè)最優(yōu)解的情況,并不適用于組合優(yōu)化問(wèn)題的解決。 方法二通過(guò)對(duì)低于給定的的值賦予0的懲罰項(xiàng),容易造成信息的失真,并不能達(dá)到優(yōu)勢(shì)互補(bǔ)的效果。 方法三則很好的彌補(bǔ)了上面兩種方法的不足,通過(guò)對(duì)適應(yīng)度函數(shù)的設(shè)計(jì),將不滿足約束條件的組合通過(guò)適應(yīng)度函數(shù)予以篩選,從而得到了最優(yōu)的結(jié)果,很好的解決了本文提出的問(wèn)題。 3? 結(jié)論 本文通過(guò)對(duì)遺傳算法中編碼和適應(yīng)度函數(shù)的設(shè)計(jì),將約束條件通過(guò)適應(yīng)度函數(shù)來(lái)體現(xiàn),有效的解決了從N個(gè)候選方案中選擇M個(gè)的最優(yōu)組合優(yōu)化問(wèn)題。同時(shí)本文將線性加權(quán)法、?姿截集標(biāo)準(zhǔn)化矩陣法與本文提出的方法進(jìn)行了對(duì)比。結(jié)果發(fā)現(xiàn):本文提出的改進(jìn)的遺傳算法在解決約束條件下的組合優(yōu)化問(wèn)題方面更優(yōu),更符合現(xiàn)實(shí)意義,從而驗(yàn)證了算法的有效性。 參考文獻(xiàn): [1]苑立偉,等.改進(jìn)遺傳算法及其在背包問(wèn)題中的應(yīng)用[J].系統(tǒng)工程與電子技術(shù),2005,27. [2]張大斌,等.基于群體編碼方式的遺傳算法求解裝箱問(wèn)題[J].計(jì)算機(jī)工程與設(shè)計(jì),2008,29. [3]賀永興,楊瑞,唐偉,歐新良.基于重構(gòu)變異算子遺傳算法的研究[J].計(jì)算機(jī)技術(shù)與發(fā)展,2015,25. [4]王翯華,朱建軍,姜方桃.供應(yīng)鏈協(xié)同視角下我們大型客機(jī)供應(yīng)商選擇評(píng)價(jià)指標(biāo)設(shè)計(jì)[J].價(jià)值工程,2015,12.

