匯率貨幣模型的非線性協整關系檢驗
——基于深度GRU神經網絡

陸曉琴，馮 玲，丁劍平，3

(1.上海財經大學金融學院，上海 200433；2.嘉興學院，浙江 嘉興 314001；3.上海國際金融與經濟研究院，上海 200433)

1 引言

匯率變動不僅從宏觀層面上影響一國的政策制定，也從微觀角度影響投資者的收益。因此，匯率貨幣模型的研究無論對于經濟理論還是政策實踐都有著重大的意義。學術界有關宏觀基本面影響匯率波動的研究可以追溯到20世紀七十年代中期，Frenkel[1]，Mussa[2]和 Bilson[3]提出了彈性價格貨幣模型(FPMM模型)，從理論上分析了貨幣供給、實際收入及長期利率水平對匯率造成的影響。之后較多的文獻基于該理論模型及其理論模型變體進行了實證研究。但在實證檢驗中，并沒有得到一致的結論。其支持方普遍認為，貨幣模型對某些國家某個時間段的檢驗是有效的，且使用面板數據能較好實現匯率與經濟基本面之間的長期均衡關系，其中外商直接投資(FDI)、生產率等也會影響匯率，認為無約束下的貨幣模型勝過隨機游走及其他模型[4-8]。

而作為理論模型的反對方，Meese和Rogoff[9-10]和Cheung等[11]都指出貨幣模型的解釋力是非常差的，文[12-14]進一步驗證了理論模型檢驗效果不佳。Din?erAfat[15]則對經濟合作與發展組織(OECD)成員國數據進行了協整檢驗，也指出傳統理論模型存在不足。

總體來看，有關匯率貨幣模型的研究，無論是支持方還是反對方、短時間檢驗或者長時期測度，現有文獻主要關注匯率與經濟基本面之間的長期線性關系。而在線性回歸預測或線性協整檢驗結果不理想的情況下，學術界傾向認為理論模型存在失效。然而現實經濟系統中，非線性關系才是最普遍的，當假設為線性時，檢驗通常是低效力的[16]。所以線性檢驗結果不理想，是否有可能源自于線性方法并不足以捕捉宏觀基本面和匯率之間的關系？事實上，理論模型普遍推測宏觀基本面和匯率波動之間存在非線性關系，即便是最簡單的購買力平價理論，也認為匯率和宏觀基本面之間存在非線性關系，而居于學術前沿的一般均衡理論模型更是認為匯率和宏觀基本面之間存在非常復雜的非線性關系。近年來，有關匯率和宏觀基本面的研究，也逐漸轉向非線性協整關系[17-18]。計算機領域機器學習的發展更是為探討匯率和宏觀基本面之間的非線性關系提供更加可靠的工具。本文即旨在通過使用機器學習中的GRU循環神經網絡，以挖掘匯率和宏觀基本面之間的非線性關系，為理解匯率理論提供新的證據。

非線性協整旨在研究序列之間長期非線性均衡關系，最早由Meese和Rose[19]、Granger[20]運用線性可加模型對協整進行了拓展。張喜彬等[21]、孫青華[22]等對非線性協整的存在、及其各分整序列的非線性協整性質進行了相關研究。檢驗非線性協整的關鍵在于非線性協整模型的構造。為此，張喜彬等[21]提出使用神經網絡來構造非線性協整模型。這為多變量非線性均衡關系的研究提供了理論工具。相關文獻使用神經網絡對1999年1月4日至2001年12月31日年間的上證綜合指數(SH)和深證成分指數(SZ)數據進行非線性協整檢驗，發現檢驗結果比線性協整檢驗結果好，在線性協整未找到協整關系的情況下，運用神經網絡方法捕捉到了兩指數之間的長期非線性協整關系[23-24]。

近年來，隨著智能時代來臨及金融數據分析需求提升，深度學習已成為金融領域的應用前沿[25]。深度學習中對時序數據具有較強記憶與智能逼近能力的長短期記憶神經網絡(Long Short-Term Memory，簡稱LSTM)，門控循環單元神經網絡(Gated Recurrent Unit，簡稱GRU)等循環神經網絡模型，為構建非線性協整模型，探討長時間序列貨幣模型的非線性均衡關系提供了一條新思路。已有文獻采用傳統神經網絡來研究變量之間的非線性協整關系[23,26]。但傳統神經網絡只做簡單的特征提取，且偏好截面數據分析，不適合研究長時間序列之間的非線性均衡關系，因為后者強調時間軸上的相關性，比之傳統神經網絡，GRU和LSTM循環神經網絡的優勢在于可以進行更為復雜的多層特征提取，挖掘時間軸上的特性，更適合研究長時間序列關系。因為深度LSTM和GRU循環網絡具有強大的學習能力和建模能力，在時序經濟數據建模中有著較大的優勢，所以經濟學文章傾向使用此類模型去預測股票市值變化、通貨膨脹等等[27-28]。尤其GRU模型作為循環網絡的最新變體，其特殊的門結構能夠有效地解決長短時間序列上的變化問題，大大的降低了運算量，成為了時序數據建模的有效工具[29-34]。但比較遺憾的是，目前尚無經濟學文章將GRU引入非線性協整建模工作中。本文希望可以起到拋磚引玉的作用，將GRU引入經濟學工作中，以擴展宏觀經濟學中協整實證檢驗的工具箱。

本文運用深度GRU神經網絡對彈性價格貨幣模型(Flexible price monetary model)、前瞻性貨幣模型(Forward-looking monetary model)和實際利率差模型(The Real Interest Differential Model)三個經典理論貨幣模型進行非線性協整檢驗，考察浮動匯率制國家的匯率和宏觀基本面之間是否存在長期非線性均衡關系。基于理論模型是小國經濟體，且資本自由流動的前提假設，本文選擇三組韓元貨幣對，同時考慮到與一般文獻較多選擇美元貨幣對形成對比，本文還選擇了三組美元貨幣對。所以，本文研究的六組貨幣對所對應的國家分別為：美國與英國、美國與日本、美國與歐盟、韓國與澳大利亞、韓國與加拿大、韓國與墨西哥。研究發現GRU神經網絡較好的找到了匯率與基本面序列間的長期非線性均衡關系，匯率的貨幣模型在非線性條件下是有效的。

2 匯率的貨幣模型

2.1 匯率的貨幣模型介紹

本小節介紹三種經典的匯率貨幣模型，分別為：彈性價格貨幣模型(FPMM)、前瞻性貨幣模型(FLMM)和實際利率差模型(RIDM)。除非特別說明，本部分所有帶*變量代表國外變量。

第一，彈性價格貨幣模型(Flexible price monetary model)，簡稱FPMM模型或稱為Frenkel-Mussa-Bilson模型[1-3]。該模型的理論基礎是凱恩斯貨幣需求函數和購買力平價(PPP)。具體數學表達式為：

(1)

其中，Et,Pt,Mt,Yt,rt分別代表匯率，商品價格，貨幣供給，收入和利率。k,α為貨幣需求對收入和利率的彈性系數，并且假定國內外相等。

第二，前瞻性貨幣模型(Forward-looking monetary model)，簡稱FLMM模型。該模型是在FPMM模型的基礎上進行修正，并且假定理性匯率預期，以及兩國貨幣需求對收入和利率的彈性系數相同(即k=k*,α=α*)，數學表達式為：

(2)

第三，實際利差模型(The Real Interest Differential Model)，簡稱RIDM模型。該模型是Dornbusch[35]和 Frankel[36]在FPMM模型和FLMM模型的基礎上進行修正。表達式為：

(3)

其中st、lt分別表示為短期利率和長期利率，ρ表示匯率調整到均衡的速度，主要取決于價格的粘性程度。

2.2 對三個模型的思考

本小節的分析顯示，三個經典模型中，匯率同宏觀基本面變量之間存在非線性關系。但技術發展的不足，使得文獻在進行相關探討時，往往采用取自然對數一階展開的方式得到線性關系，以允許經典線性計量工具(如線性回歸、線性協整等)能夠對模型進行驗證。而較多文獻對(1)式、(2)式、(3)式取自然對數進行線性實證檢驗時，結果都不令人滿意，例如表1。

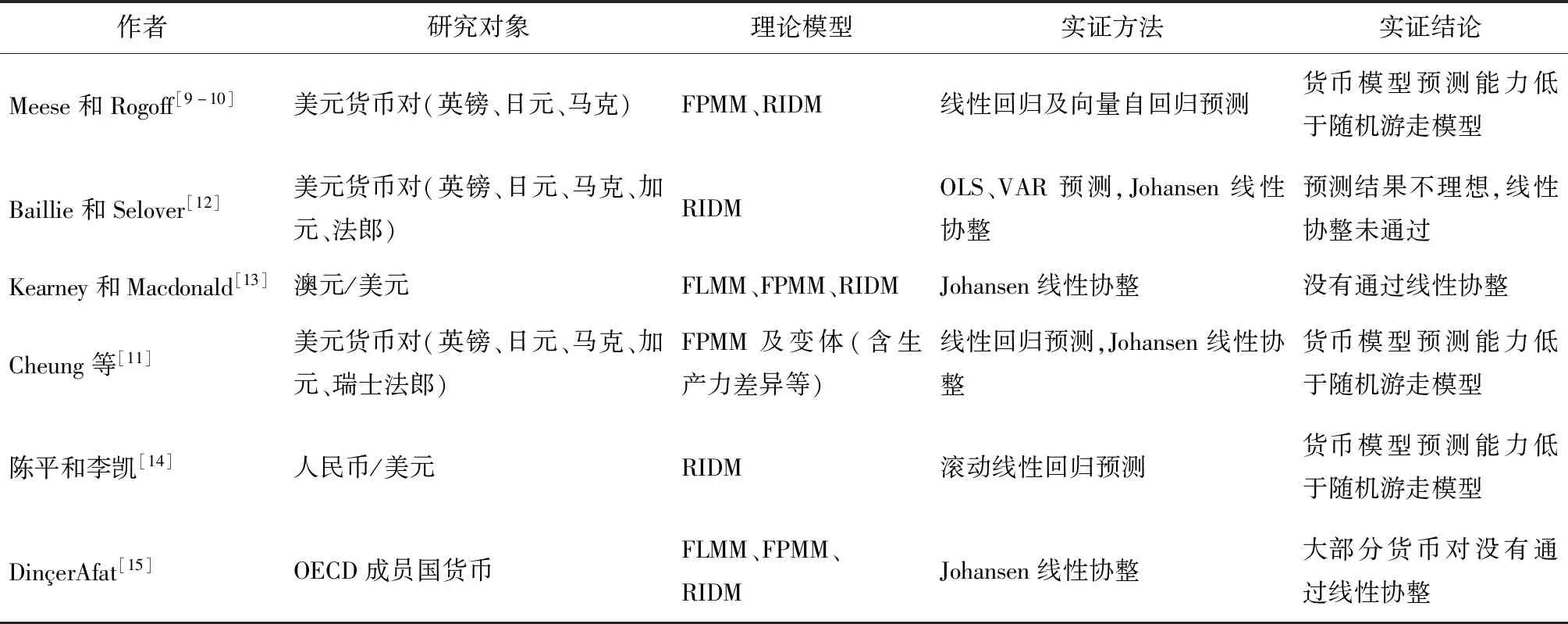
表1 相關貨幣模型實證研究失效的情況

隨著計量經濟學和電腦技術的發展，學術界可以使用新的計量方法(如非線性回歸、非線性協整等)來尋找不同變量之間的相關性。那么，我們是否有可能在前人研究的基礎上，利用新技術，找到匯率與宏觀基本面之間的長期非線性關系？得到一致的實證結論？GRU等循環神經網絡模型的發展，則使得人們可以對數據進行深度學習，進一步挖掘時序數據中的記憶功能。為此，本文嘗試利用深度GRU技術探討匯率與宏觀基本面之間的長期非線性協整關系。

3 基本方法

非線性協整檢驗方法主要有推廣的E-G兩步法、秩檢驗法、記錄數協整檢驗及神經網絡等方法。其中，神經網絡方法可以無限逼近未知的非線性結構，具有較其他方法更好的檢驗效果。為此，本文借鑒張喜彬等[21]、樊智等[23]、許啟發[37]、黃超等[38]用神經網絡構建非線性協整函數的方法，試圖找尋理論所預測的匯率與基本面之間非線性協整關系。首先對序列進行長記憶特性檢驗，因為如果數據序列之間存在非線性協整關系，那么意味著序列數據一定要具有長記憶特性才可以。其次，具體采用深度GRU神經網絡的方法來構建非線性協整函數。深度GRU神經網絡繼承了一般神經網絡自主學習、智能逼近的能力，同時還具有普通神經網絡所不具備的傳遞記憶功能，更具有對時序數據挖掘上的優勢。最后，檢驗所構建的GRU模型殘差是否為短記憶序列(SMM)。若殘差為短記憶序列，則說明GRU較好的吸出了序列間的非線性特性，證明序列間存在非線性協整關系。

3.1 序列長記憶檢驗

對于長記憶序列(LMM)的檢驗，最早由Hurst[39]提出用重標極差分析法(rescaled range analysis，簡稱經典R/S)來分析時間序列的長記憶性，后由Lo[40]進行修正：

(4)

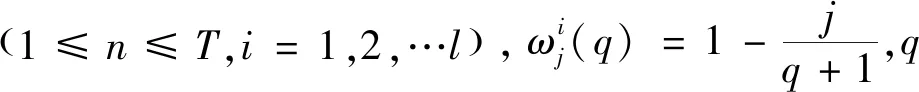
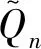
Lloyd等[41]研究表明，當n無限增大時，重標極差統計量Qn可用經驗公式表示：

Qn=R/S=θnH

(5)

其中，θ為常數，H為Hurst指數。對(5)式兩邊取對數，得到：

log(R/S)=log(α)+Hlog(n)

(6)

繪制log-log圖，OLS擬合(log(R/S),log(n))，就可以求出Hurst指數。當Hurst指數大于0.5時，說明序列具有長記憶性。

彼得斯[42]研究指出，Hurst指數與差分階數d還存在如下關系：H=0.5+d。因此，通過Hurst指數可以求得差分階數d。若所得d為分數(0≤d≤1)，則認為序列具有長記憶特性。

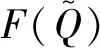
3.2 深度GRU構建非線性協整函數

GRU神經網絡由 Cho等[29]提出，用于序列數據建模。根據非線性協整系統的特點，構建圖1的GRU神經網絡模型。

在每個時刻t(t=1,2…T)，網絡分為輸入層、隱藏層和輸出層三層，輸入層與隱藏層、隱藏層與輸出層之間用不同的權重值來連接。其中，輸入層Xnt=(x1t,x2t,…,xNt)表示N維輸入向量(n=1,2…N)；隱層神經元數為m個L模塊(圖1表示每個時刻有m=1個神經元L模塊，多個神經元只需重復疊加，并用不同權重連接輸入向量和輸出向量即可)，其中(m=1,2…M)；輸出層為1維yt。本文在FLMM模型中，設置輸入層由兩國匯率、貨幣供給之差、收入之差構成的3維(n=3)輸入向量X3t=(e1t,m2t,y3t)T，FPMM模型中，設置輸入層由兩國匯率、貨幣供給之差、收入之差及長期利率差構成的4維(n=4)輸入向量X4t=(e1t,m2t,y3t,l4t)T，RIDM模型中，設置輸入層由兩國匯率、貨幣供給之差、收入之差、短期利率差及長期利率差所組成的5維(n=5)輸入向量X5t=(e1t,m2t,y3t,s4t,l5t)T；基于隱層神經元數不超過觀測值三分之二及極小化誤差的原則，將隱層神經元數控制在150(m=1,2…M，M≤150)以內進行調試；輸出層為1維yt。

在t時刻，從n維輸入層向量到m個隱層神經元L模塊的連接權重為νnmt，從m個隱層神經元L模塊到輸出層yt的連接權重為ωmt，(t=1,2,…,T)，(n=1,2,…,N)，(m=1,2,…,M)，因此FLMM、FPMM及RIDM模型中需要學習的主循環參數向量分別為νnmt,ωmt。

經典循環神經網絡L模塊只是一個tanh函數，而GRU神經網絡L模塊是復雜的門限結構，網絡不僅要自主學習并調節以上主循環的參數向量，還要學習每個單元門限結構中重置門、更新門及候選記憶單元中的參數向量，能夠更有效的挖掘數據中的記憶功能。以隱層神經元節點為1(即m=1)時分析，其實現的單個L模塊單元映射關系如下：

重置門：zt=δ(WnztXnt+Wztht-1+bzt)

更新門：rt=δ(WnrtXnt+Wrtht-1+brt)

輸出層：yt=δ(ωt*ht)

其中，δ為激活函數(通過對網絡調試，選擇非線性的sigmoid函數或tanh函數)。zt和rt分別為重置門和更新門。Wnzt和Wnrt分別代表重置門zt和更新門rt中輸入向量Xnt=(x1t,x2t,…,xNt)的權重，Wzt和Wrt分別代表重置門zt和更新門rt中上一時刻記憶單元ht-1的權重，bzt和brt分別表示重置門zt和更新門rt中的偏置(截距項)，Wrht和Wnrht分別表示候選記憶單元中上一時刻記憶信息rt*ht-1和當期輸入向量Xnt=(x1t,x2t,…,xNt)的權重。因此，FLMM、FPMM及RIDM模型在L模塊單元中需要學習權重向量Wnzt、Wnrt和偏置bzt、brt。

網絡學習按照極小化誤差來實現：

(7)

其中輸出層指導值序列{Dt}選擇以序列樣本Xnt的平均值為均值的白噪聲時間序列[37]。通過自主學習循環權重和每個L模塊單元中的權重，能夠較好的實現網絡誤差極小化，實現對過往信息的深度記憶學習，從而構建有效的非線性協整函數。

在模型極小化誤差過程中，本文主要采用RMSprop優化器來實現，在無法獲得最優解的情況下，選用Nadam優化器進行調試。RMSprop優化器是將學習率η替換為η除以平方梯度的指數衰減平均值。而Nadam優化器是對學習率和梯度方向都添加了衰減項。這兩種優化器能防止時間序列信息傳遞過程中的衰減難題，具有更高的學習效率。同時，為了提高學習效率，我們也在輸入層設置了丟棄率dropout(維持在0.2-0.3進行調試)，即暫時丟棄個別神經單元以提高學習速率。

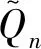
4 實證研究

4.1 數據的選取及基本描述

根據第二部分的匯率貨幣模型和第三部分的基本方法，本節分別對FLMM、FPMM、RIDM三個理論模型進行非線性協整檢驗。本文選取美國與英國(USA-UK)、美國與日本(USA-JP)、美國與歐盟(USA-EU)、韓國與澳大利亞(KOR-AUS)、韓國與加拿大(KOR-CAN)、韓國與墨西哥(KOR-MEX)六組典型浮動匯率制國家的貨幣對進行實證檢驗，并采用月度數據進行分析。M1和工業生產指數分別為理論模型中的貨幣供給數據(M)和實際收入數據(Y)，并經過季節性調整。理論模型中的短期利率和長期利率均來自OECD官網給出的長短期利率數據。

所有數據來源于OECD官網，除了墨西哥長期利率用墨西哥央行提供的3年期國債收益率替代，美元與歐元匯率由Wind數據庫給出的日度數據取均值得到。此外，考慮數據的可得性，有韓元參與的貨幣對樣本區間統一為2000年10月至2017年10月，美國與英國的樣本區間為1986年10月至2017年11月，美國與日本的樣本區間為2002年4月至2017年11月，美國與歐盟的樣本區間為1999年1月至2017年11月。

除利率外對所有數據取自然對數，考慮到數據量綱不同及數量級差別較大，會影響神經網絡訓練精度，因此，在此基礎上再對所有數據進行歸一化處理：

(8)

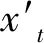
基于數據準備，本文先運用常規Johansen線性秩檢驗方法，對三種理論模型六組貨幣對進行線性協整檢驗。表2匯報了線性協整秩檢驗的跡統計量結果(最大特征值檢驗結果相同，介于篇幅限制，沒有匯報，有需要的讀者可問作者索要)。由表2可知，韓元和澳元貨幣對的三個理論模型，美元和英鎊貨幣對、韓元和加元以及韓元和比索貨幣對的部分理論模型都沒有通過線性協整檢驗。這說明僅用線性檢驗方法不足以捕捉宏觀基本面和匯率之間的關系。因此，有必要進一步探究序列間的非線性協整關系。

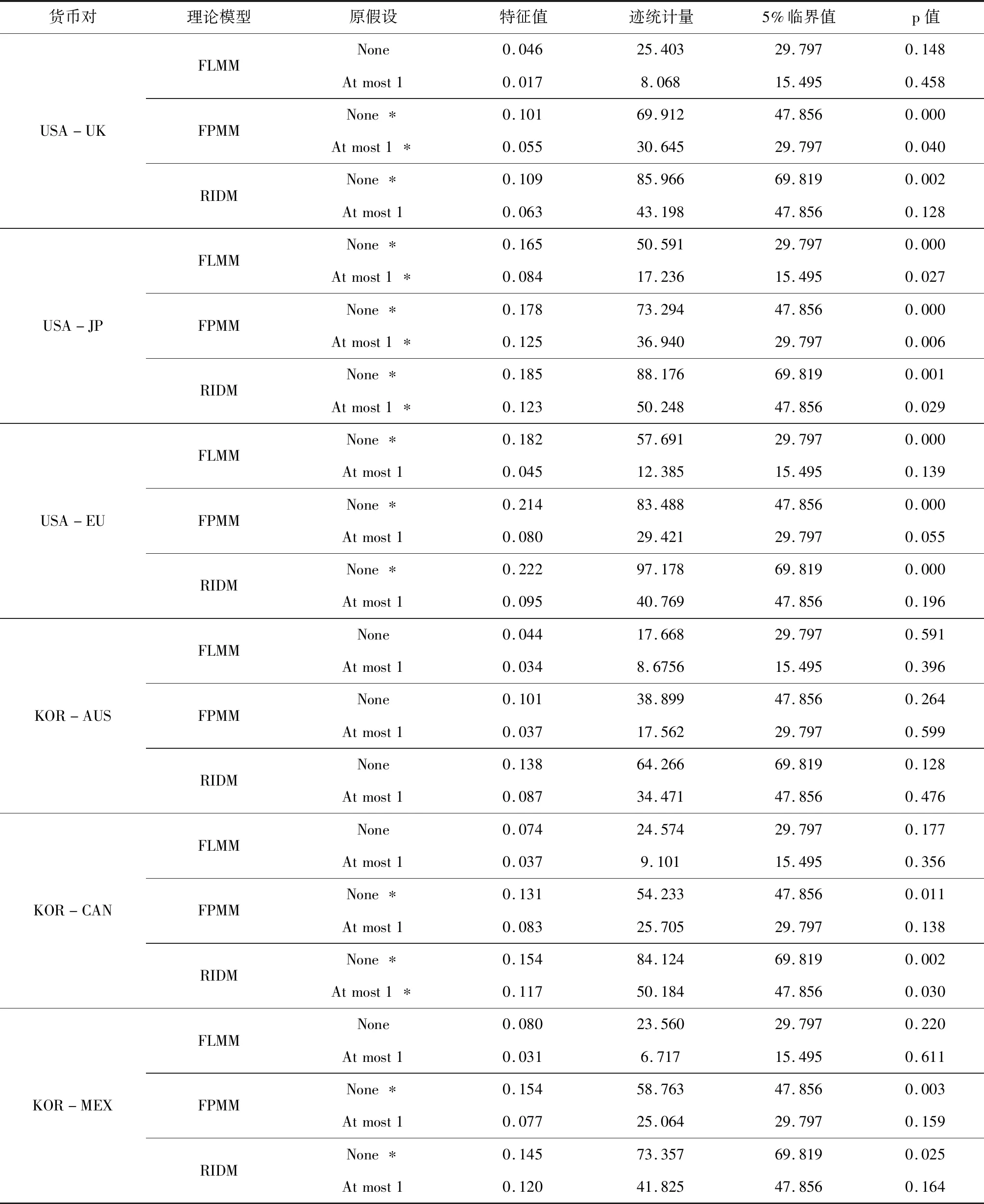
表2 線性協整檢驗結果

4.2 序列的長記憶性檢驗

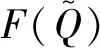
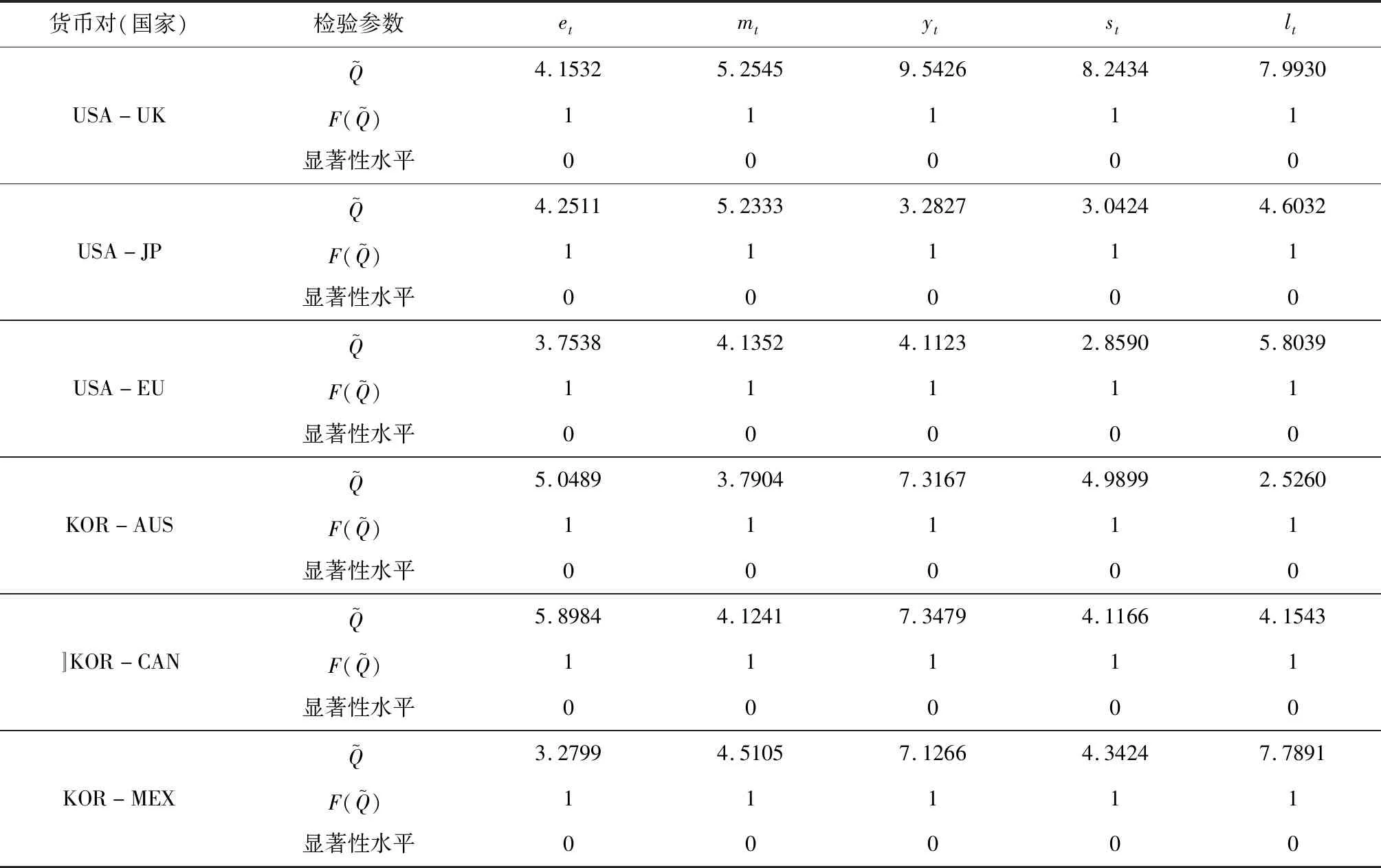
表3 匯率及宏觀經濟基本面序列的長記憶檢驗

由表3可知，在零假設為短記憶的顯著性水平都為0，說明拒絕原假設的出錯概率為0，六組國家的匯率及基本面各序列都為長記憶序列。

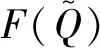
Bailie等[45]、鐘正生和高偉[43]等認為還應該進一步用差分階數d來驗證序列的長記憶特性。為此，由彼得斯[42]所提出的H=0.5+d關系式，得到差分階數d(見表4)。

由表4結果顯示，六組國家的匯率與各經濟基本面序列的差分階數不是整數，而是分數，并且差分階數各不相同，說明各序列為長記憶序列。

通過以上三種方法驗證了經過歸一化后的六組國家的匯率與各經濟基本面序列都具有長記憶特性。因此依據文[46]，線性協整理論將不再適用，應運用非線性協整理論來討論匯率與經濟基本面之間的關系。

4.3 非線性協整檢驗

接下來運用GRU神經網絡來探測序列之間是否存在非線性協整關系。分別對六組國家序列數據的FLMM、FPMM、RIDM三個理論模型進行非線性協整檢驗。

4.3.1 非線性協整模型的構建

本文在Python的pycharm軟件上構建GRU基本網絡模塊，并實現對網絡的訓練和學習。根據第三部分的基本方法，通過選擇非線性激活函數，調節隱層神經元數，主要選擇rmsprop優化器，在無法實現最優時嘗試namth優化器，輸入層采用丟棄率dropout，同時調節教師指導值{Dt}，最終實現了最大迭代次數1000次下的極小化誤差。具體見表5。

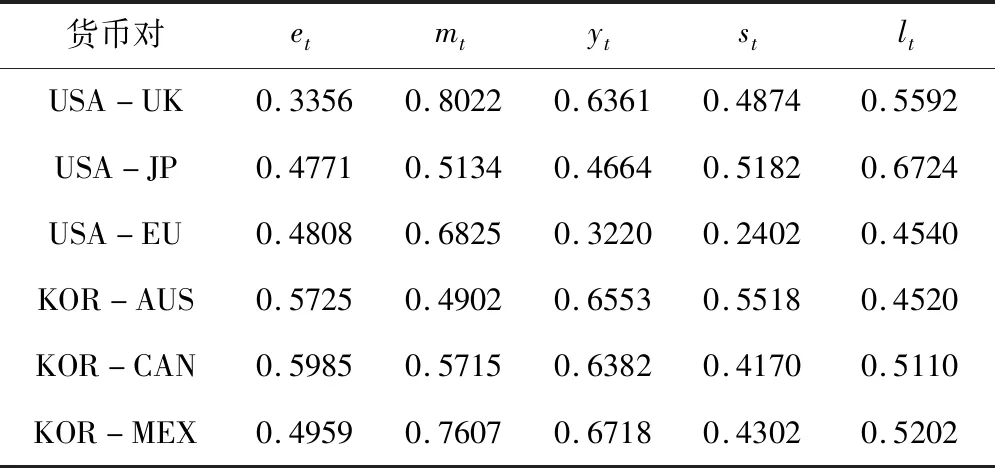
表4 樣本序列差分階數d

從表5看出，各模型的極小化誤差都在0.03以下。并且模型時間序列殘差波動較為平緩，除USA和UK的FLMM模型殘差值的標準差是-0.0121，其余所有模型殘差值的標準差都是四位小數，這些結果都說明模型得到了較好的訓練，匯率與各經濟基本面序列有了較好的擬合。另外，文章在進行模型調試過程中，激活函數曾嘗試選用線性函數linear，但實現的誤差值都較大，而改用非線性激活函數sigmoid或者tanh時，大大降低了誤差值，再次說明匯率與基本面序列間是非線性關系，而不是線性關系。

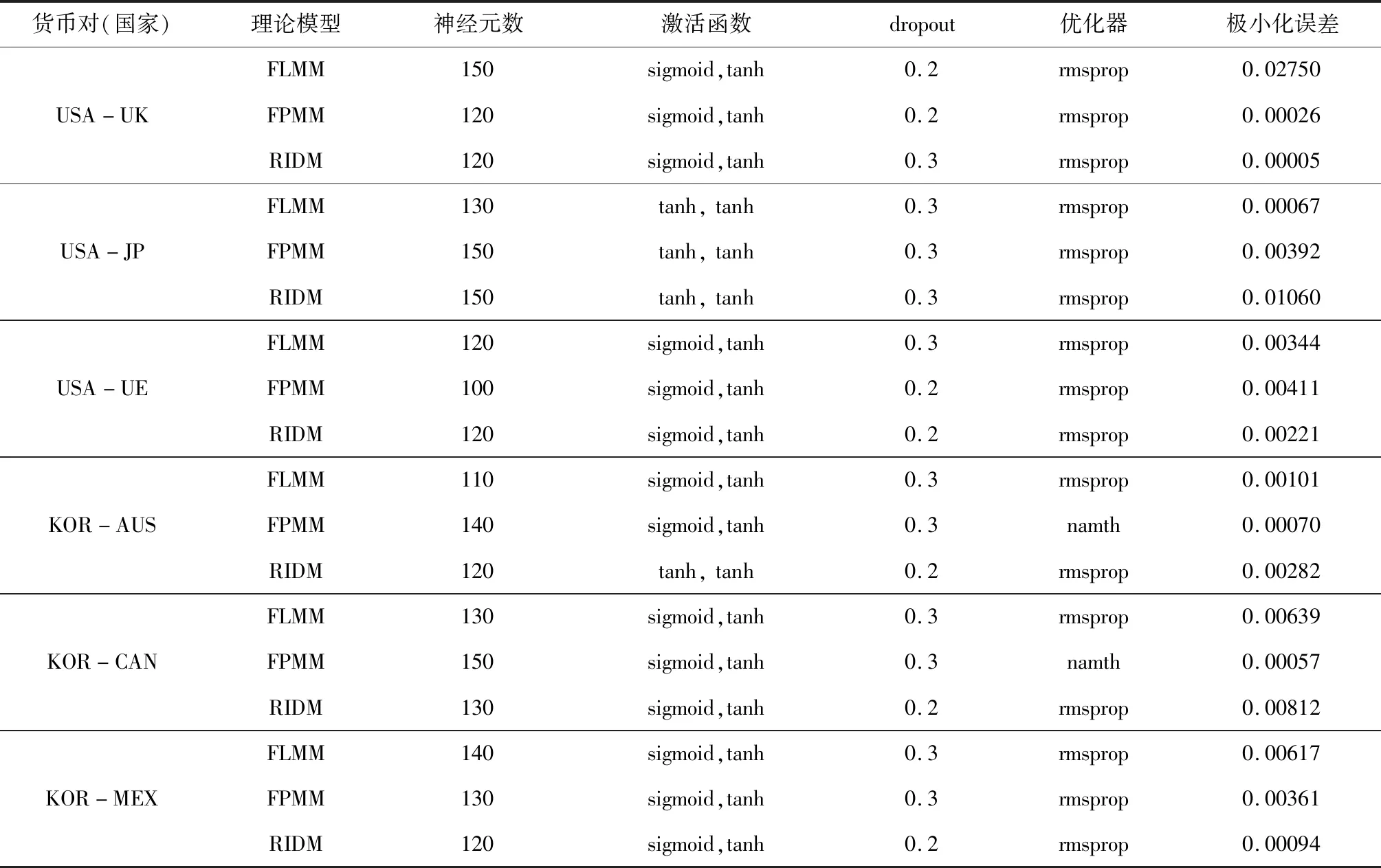
表5 各國最優深度GRU協整模型

4.3.2 殘差的短記憶檢驗

接下來需要檢驗GRU模型擬合后的殘差序列是否為SMM序列。按照理論，如果是SMM序列，則說明他們之間存在非線性協整關系，否則不存在非線性協整關系。依然采用Lo(1991)[40]提出的修正R/S可知(具體見表6)，六組國家的三個理論模型擬合后的殘差序列的顯著性水平都高于10%，拒絕原假設為短記憶序列出錯的概率較大，有的甚至達到100%的概率，即在10%的顯著性水平下都不顯著，因此拒絕備擇假設，接受原假設，可判斷各殘差序列為SMM序列。說明匯率與經濟基本面序列間都存在非線性協整關系，所構建的GRU網絡為非線性協整函數。從另一個層面來講，鑒于GRU神經網絡強大的非線性時序數據逼近能力，為匯率貨幣模型找到了長期均衡的非線性關系。

4.4 對比分析

為能更好的說明本文所提方法的有效性，接下來將線性協整檢驗結果和非線性協整檢驗結果進行對比分析(具體見表7)。由表7可知，針對部分貨幣對，某些理論模型無法通過線性協整檢驗，但所有模型均可以通過GRU非線性協整檢驗。這意味著，匯率和宏觀基本面之間存在著線性協整檢驗所無法捕捉到的非線性協整關系。本文運用先進的GRU智能技術較好的找到了匯率與宏觀基本面之間的非線性協整關系，驗證了理論模型的有效性。此外，與已有文獻進行比較，我們發現針對本文所使用的三組美元貨幣對，文獻在進行協整檢驗時，往往沒有統一結論。如Georgoutsos和Kouretas[47]發現美元與歐元貨幣對的FLMM模型不存在協整關系，當加入需求和生產力因素時，則存在協整關系， Din?er Afat[15]發現該組貨幣對的FLMM模型和FPMM模型都不存在協整關系，但RIDM模型存在協整關系；Cerra和Saxena[6]發現美元與日元、美元與英鎊貨幣對的FLMM模型存在協整關系，但Baillie和Selover[12]發現該組貨幣對的RIDM模型不存在協整關系。本文在進行線性協整檢驗時，發現美元與歐元、日元、英鎊貨幣對的FPMM模型、RIDM模型存在線性協整，美元與日元、歐元貨幣對的FLMM模型也存在線性協整，而美元與英鎊貨幣對的FLMM模型不存在協整關系。但當本文使用GRU神經網絡進行檢驗時，所有貨幣對均存在非線性協整關系。

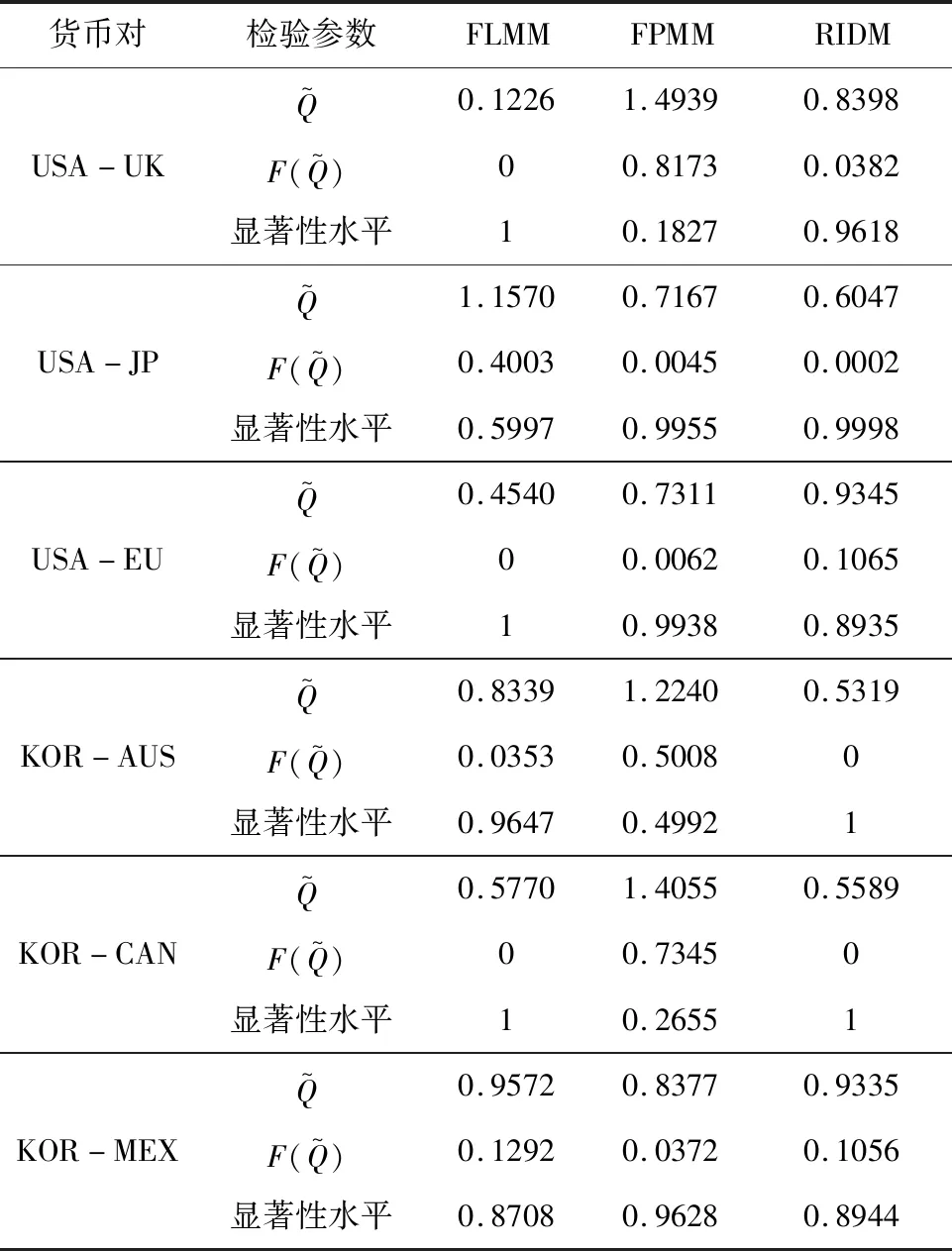
表6 殘差短記憶檢驗

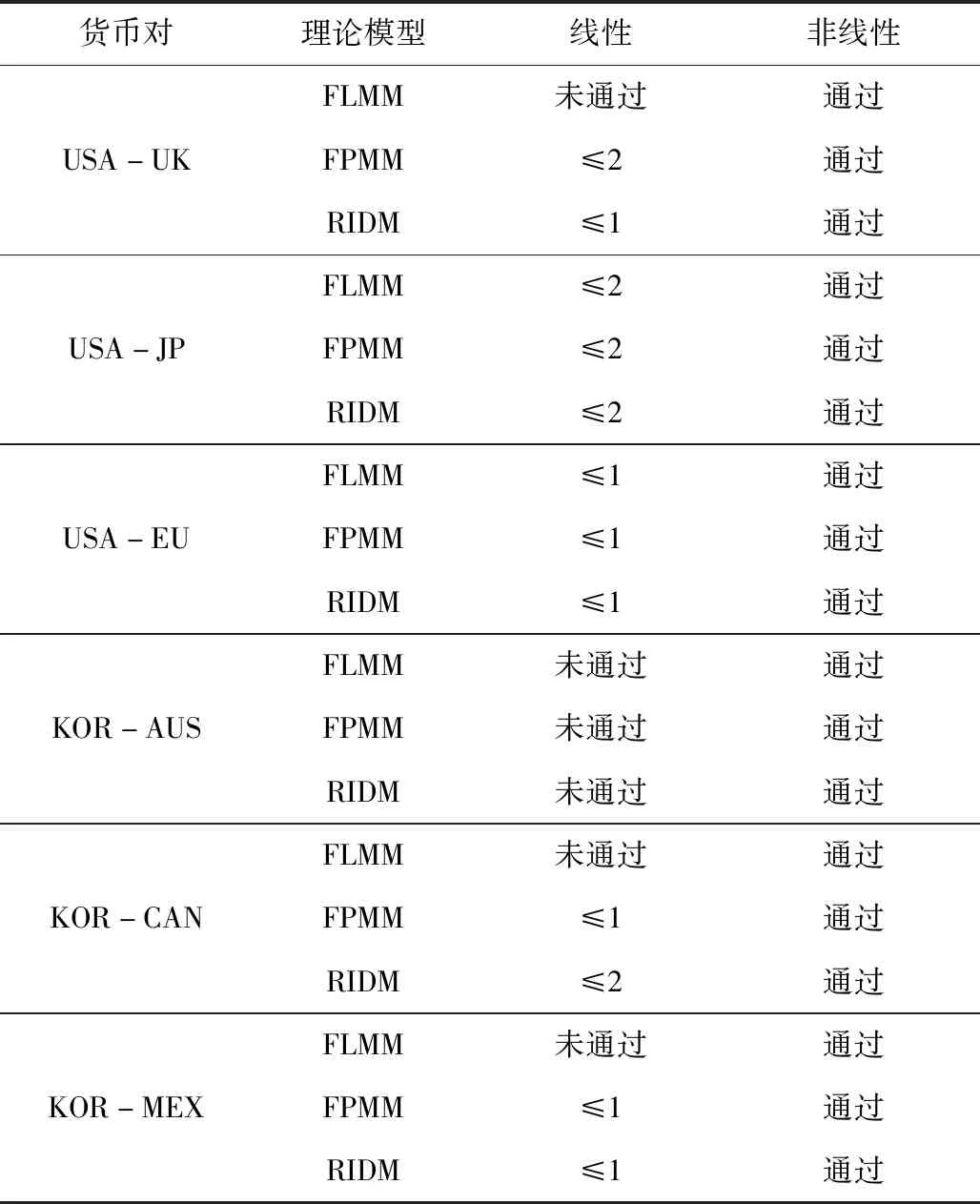
表7 線性協整與非線性協整檢驗結論對比

注：≤1和未通過分別表示在0.05%的置信度水平上，最多存在1個線性協整方程和不存在線性協整方程。

5 結語

匯率的貨幣模型一直是學術界和理論界探討的焦點。至今，有較多的學者對匯率的貨幣模型進行線性協整檢驗，其結果不令人滿意。非線性協整理論是線性協整理論的擴展，能夠更好的刻畫多變量序列間的非線性均衡關系。本文首次基于非線性協整的視角，來探測匯率與宏觀經濟基本面之間的非線性關系。論文發現，在進行歸一化后的原序列是存在長記憶特性的，適合采用非線性協整理論進行探討。

但非線性協整函數的構建是一個重要難題。為此，本文運用人工智能方法，用GRU神經網絡來逼近非線性協整函數，對六組典型浮動匯率制國家貨幣對(美元/英鎊、美元/日元、美元/歐元、韓元/澳元、韓元與加元、韓元/比索)進行非線性協整檢驗，考察FPMM、FLMM和RIDM三個理論模型非線性條件下的有效性。研究結果顯示：匯率與宏觀經濟基本面序列都是長記憶序列，GRU神經網絡較好的找到了匯率與基本面序列間的長期非線性均衡關系。因此，本文驗證了在非線性條件下，匯率的貨幣模型是有效的。進而，通過與傳統線性協整檢驗結果及現有文獻對比，本文不僅驗證了深度GRU技術在非線性協整分析中的有效性，也突顯了具有強大學習能力的深度GRU技術在經濟建模中的優勢。

本文主要側重于研究GRU智能技術檢驗匯率貨幣模型的有效性，在后續的工作中，我們將進一步探究和檢驗該模型是否具有一定的預測能力。另外，我們也會考慮將GRU技術運用于新興市場等其他國家貨幣對的檢驗和預測，以進一步驗證本文所提方法在實踐上的普遍意義。