柱形匯聚幾何中內爆驅動金屬界面不穩定性*

王 濤，汪 兵，林健宇，鐘 敏，柏勁松，李 平，陶 鋼

（1. 中國工程物理研究院流體物理研究所，四川 綿陽 621999；2. 南京理工大學能源與動力工程學院，江蘇 南京 210094）

當沖擊波或慣性力加載不同物質間的擾動界面時，界面會失穩并發生擾動增長的現象，前者稱為Richtmyer-Meshkov（RM）不穩定性[1-2]，后者稱為Rayleigh-Taylor（RT）不穩定性[3-4]。其中RT 不穩定性與加載方向有關，只有當輕介質加速重介質時才會發生。界面不穩定性在諸多領域有重要的應用背景，如慣性約束聚變[5-6]、超新星爆炸[7]、小行星撞擊[8-9]、地球內核運動及板塊構造[10-11]等，因此具有重要的研究意義。

Wang 等[12-18]、Bai 等[19-21]、Xiao 等[22]長期研究流體介質界面不穩定性及湍流混合演化規律和統計特性。Liu 等[23]通過直接數值模擬，研究了RM 不穩定性和湍流混合中的能量傳遞過程和機制。李俊濤等[24-25]也通過數值模擬，研究了弱沖擊波加載V 形界面導致的RM 不穩定性中的渦動力學行為特性及作用機制。Luo 等[26-27]、Si 等[28]、Ding 等[29]、Lei 等[30]在匯聚沖擊波誘導下的氣體界面不穩定性實驗研究方面成績卓越，特別是首次測得了柱形單模態air/SF6界面的擾動振幅。在我國，有關界面不穩定性的研究主要集中在流體介質方面，很少涉及金屬材料界面不穩定性，而界面不穩定性也會在金屬材料中發生。而且，金屬材料的復雜物性，如強度、相變、損傷、微結構等，使金屬材料界面不穩定性比流體界面不穩定性更復雜，因此，金屬材料界面不穩定性是一種跨尺度多物理耦合的復雜流動問題。

金屬材料界面不穩定性的理論研究，主要基于能量平衡[31-33]或力平衡[34-36]，推導擾動增長所滿足的色散關系，但是，這些線性理論分析均采用了理想塑性本構關系，預測擾動增長受到較大限制。我們也基于能量平衡，但采用了Steinberg-Guinan（SG）和Johnson-Cook（JC）本構模型及變壓力加載歷程，針對有限厚度金屬平板問題，推導了相應的擾動增長方程，將線性分析方法進行了拓展，可用于平面幾何金屬不穩定性線性和非線性段增長的預測[37]。并且，對爆轟驅動和激光等離子體驅動的金屬界面不穩定性實驗進行了分析，結果和實驗吻合較好，但是，這種線性分析方法依然有較大的局限性，如它還無法考慮加載過程等。

金屬材料界面不穩定性實驗研究始于20 世紀70 年代。首先，由Barnes 等[38-39]通過爆轟驅動鋁平板實現，并采用高能X 射線裝置觀察界面擾動增長。后來，平面爆轟驅動金屬材料界面不穩定性實驗[40-42]均采用相似的裝置。在美國、俄羅斯，開展了大量有關金屬材料界面不穩定性的研究工作，包括界面擾動增長規律及影響因素的研究等。何長江等[43]通過數值模擬，研究了初始擾動波長對平面爆轟驅動金屬鋁RT 不穩定性發展的影響。郝鵬程等[44]、劉軍等[45]通過對內爆加載金屬鋼殼的數值模擬，研究了材料強度和初始波長對界面擾動增長的影響。Olson 等[46]在爆轟實驗中，研究了銅材料的微結構和加工對RT 擾動增長的影響，發現單晶晶向和材料加工導致的應變硬化會影響擾動增長，而多晶材料的晶粒尺寸和晶界強化在所研究的加載條件下對擾動增長無影響。Jensen 等[47]采用高分辨率的原位診斷技術，研究了沖擊條件下鈰的RM 不穩定性問題。Cherne 等[48]采用分子動力學模擬方法，研究了銅樣品自由面上不同形狀的二維溝槽擾動對銅/真空界面RM 不穩定性發展的影響。

金屬材料界面不穩定性增長是一種高壓高應變率條件下的大變形行為，與材料強度密切相關，宏觀表現就是材料強度可以抑制擾動增長。近幾年，基于這個思想，利用金屬材料界面不穩定性增長，研究高壓高應變率條件下的材料強度[42,49-53]，進而發展了適用性更強的材料強度模型[54]。

由以上分析，目前對于金屬材料界面不穩定性問題，雖然已經開展了較多的研究，但是還不充分不深入，仍然有很多問題有待解決。比如，理論研究很不完備，實驗研究缺乏對物理細節的直接認識，而且高分辨率診斷設備和極端加載裝置限制了實驗工作的全面開展。因此，數值模擬成為一種有效便捷的研究手段。我們長期致力于流體界面不穩定性及湍流混合問題的數值模擬研究[12-22]。在此基礎上，我們發展了適用于金屬材料大變形行為數值模擬的高保真度爆轟與沖擊動力學歐拉程序。本文中，利用自研的數值模擬歐拉程序，研究柱形匯聚幾何中內爆驅動下金屬材料界面不穩定性的動力學行為。

1 計算方法

針對考慮爆轟和材料彈塑性行為的多物質、大變形及強沖擊波物理問題，發展了高保真度的爆轟與沖擊動力學歐拉有限體積計算程序。其守恒型控制方程組為：

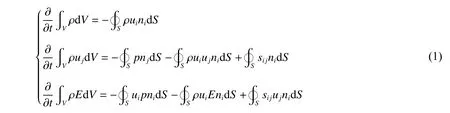
式中：下標i、j 分別代表x、y、z 三個方向，遵循張量運算法則，V 為控制體體積，S 為控制體表面積，ni為其外法向單位矢量分量，ρ、uk(k=i, j)、p、E 分別為密度、速度、壓強和質量總能量，sij為偏應力張量分量。

采用維數分裂技術，將方程組（1）描述的物理問題分解為多個一維問題，對于每個一維問題，采用PPM 方法，對單元內物理量的分布進行插值和重構；然后，通過歐拉型兩步算法進行計算，即物理量的Lagrange 推進求解，再將拉氏網格上的物理量映射到靜止的歐拉網格上。材料強度效應、炸藥爆轟過程和人工黏性在Lagrange 步中實現。多物質界面采用體積分數方法進行捕捉。

1.1 狀態方程

數值模擬中，炸藥用JWL 狀態方程描述：

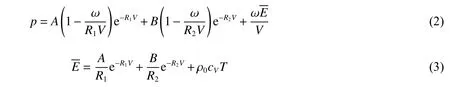
E=ρ0E′E′

式中：相對比容V=ρ0/ρ，A、B、R1、R2、ω 為常數， 為體積內能， 為比內能，cV為比熱。

金屬材料用Mie-Grüneisen 狀態方程描述：

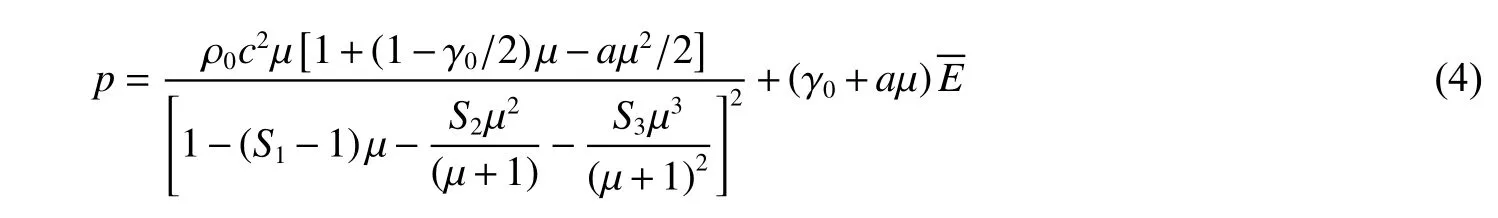
式中：相對壓縮度 μ =ρ/ρ0?1 ，ρ0為初始密度，c 為零壓聲速，γ0為Grüneisen 系數，a、S1、S2、S3為常數。

硅橡膠采用凝聚介質實用狀態方程：

式中：c0為正常態的聲速，γ 為材料參數。

1.2 本構方程

金屬材料采用SG 本構模型，它可以很好地描述高壓高應變率下的材料強度特性。SG 本構模型在彈塑性本構方程中引入壓力、溫度和應變率項，同時壓力與應變率對流動應力的耦合效應具有可分離變量特性。因為SG 本構模型中流動應力依賴于壓力，所以材料的本構方程與狀態方程之間存在某種耦合關系。這個耦合關系反映了高壓下金屬材料的壓力硬化特性。SG 本構模型的動態屈服強度和剪切模量分別為：

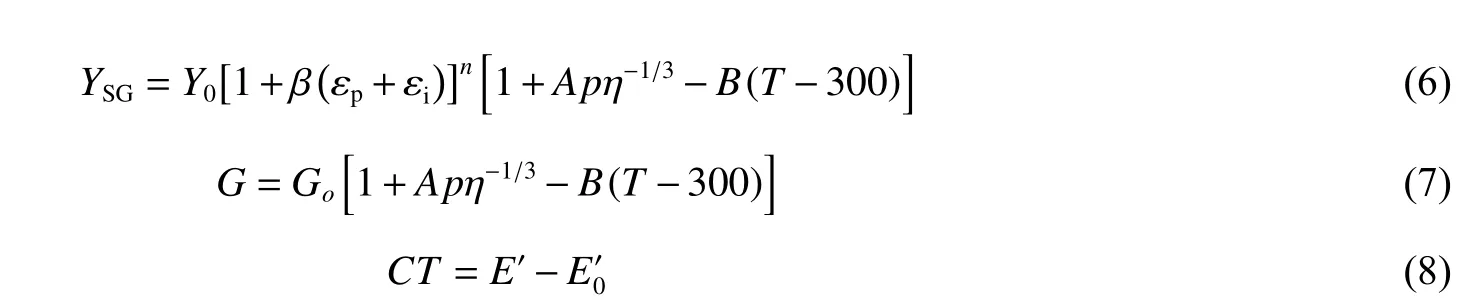
式中：Y0和G0分別為初始屈服強度和剪切模量，β 和n 分別為材料應變硬化系數和硬化指數，A 為壓力硬化系數，η=ρ/ρ0為材料壓縮比，B 為溫度軟化系數，為零溫下的比內能，C 為材料常數。

2 結果與分析

在進行柱面內爆驅動不銹鋼金屬材料界面不穩定性計算和分析前，先通過對文獻[40]中的爆轟驅動T-6061 鋁的RT 不穩定性實驗的模擬，確認本計算程序的可靠性。該實驗采用HMX 炸藥爆轟加載1.5 mm 厚的鋁樣品，加載壓力峰值為30 GPa。初始擾動波長λ0=2 mm，初始擾動振幅a0=0.15，0.11 mm。圖1 為用自研的歐拉程序計算得到的擾動振幅和文獻[40]中采用ARES 程序計算的結果，及實驗結果（橫軸是自由面運動位移）。可以看出，數據吻合較好，說明自研的歐拉程序模擬這類爆轟驅動金屬材料界面不穩定性是準確的。

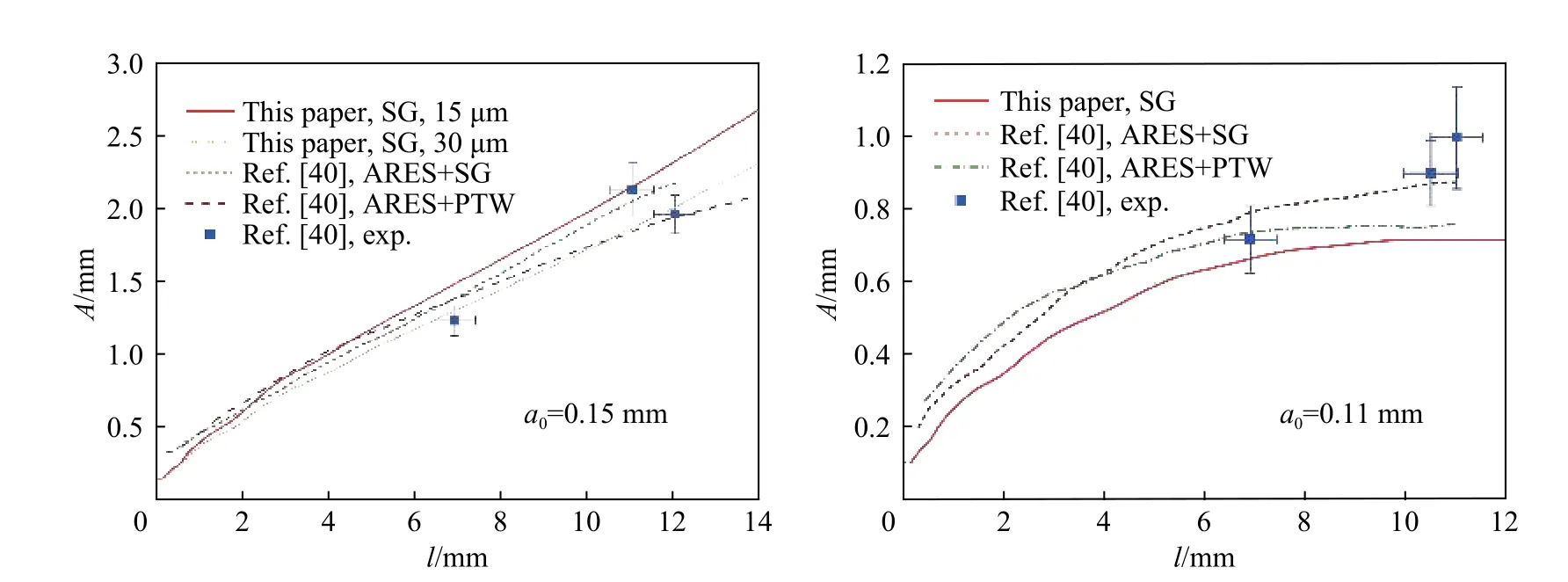
圖 1 爆轟驅動鋁實驗的擾動振幅Fig. 1 Perturbation amplitudes of experiments driven by explosion

2.1 柱面內爆計算模型和參數

以Frachet 等[55]的柱面內爆驅動不銹鋼金屬材料的雙模態擾動界面不穩定性實驗為基礎，開展柱面內爆驅動下金屬材料界面不穩定性發展演化的動力學行為特性數值模擬。

計算模型如圖2 所示：外層為炸藥，其外直徑和厚度分別為200 和50 mm，由于文獻[55]中沒有說明何種炸藥，本文中采用TNT；中心物質為直徑92 mm 的硅橡膠；中間不銹鋼殼外直徑為100 mm，厚度為4 mm，且內界面上預置有振幅0.5 mm、模數為13 和29 mm?1的雙模態初始擾動。

T N T 炸藥J W L 狀態方程參數分別為：ρ0=1.63 g/cm3，pcj=21.0 GPa，Dcj=6.93 km/s，A=371.2 GPa，B=3.231 GPa，R1=4.15，R2=0.95，ω=0.3。不銹鋼Mie-Grüneisen 狀態方程參數分別為：ρ0=7.896 g/cm3，c=4.569 km/s，γ0=2.17，a=0.47，S1=1.49，S2=S3=0；不銹鋼SG 本構模型參數分別為：Y0=0.34 GPa，Ymax=2.5 GPa，G0=77.0 GPa，β=43.0，n=0.35，A=0.022 6 GPa?1，B=0.455 kK?1。硅橡膠凝聚介質實用狀態方程參數分別為：ρ0=1.15 g/cm3，c0=1.343 km/s，γ=1.6。

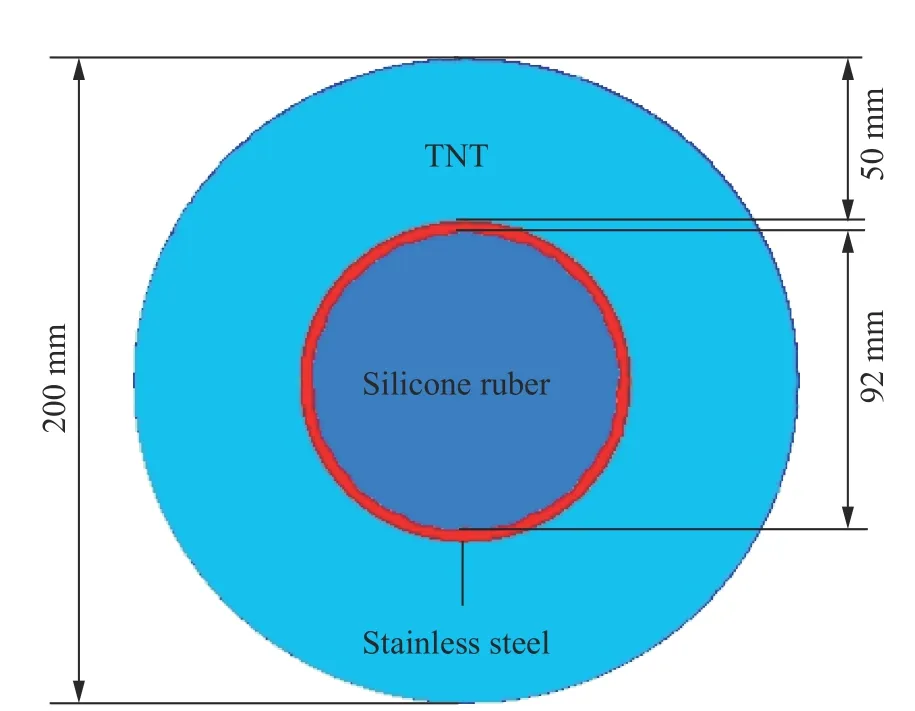
圖 2 柱面內爆驅動金屬材料界面不穩定性計算模型Fig. 2 Computational model of metal interface instability driven by cylindrical implosion

2.2 加載和界面運動特性

沖擊波(SW)由低阻抗介質向高阻抗介質方向加載物質界面時，會產生一個透射沖擊波和一個反射沖擊波；沖擊波由高阻抗介質向低阻抗介質方向加載物質界面時，會產生一個透射沖擊波和一個反射稀疏波(RW)。炸藥起爆后，產生的柱形爆轟波向內聚心運動，到達鋼殼外界面并作用后，向內產生透射沖擊波，鋼殼也開始聚心運動，由于質量守恒，鋼殼徑向厚度逐漸增大（見圖3）；該透射沖擊波約在7.8 μs時到達鋼殼內界面，形成由高阻抗介質向低阻抗介質方向的沖擊波加載，內界面加載壓力瞬間達到10 GPa（見圖4），同時向硅橡膠內產生透射沖擊波和鋼殼內的反射稀疏波；鋼殼內的反射稀疏波向外運動并加載外界面后又向內反射壓縮波(CW)，壓縮波和稀疏波會在鋼殼內多次反射，并在內外界面上分解而交替產生稀疏波和壓縮波，進而交替加載鋼殼界面，可見于鋼殼內三角形的胞格結構（見圖3）、加載壓力和內界面速度振蕩區域（沖擊波加載和稀疏波卸載效應）（見圖4、5，界面運動速度以徑向向外為正）；硅橡膠內的透射沖擊波聚心反彈后，在約20.5 μs 時到達并沖擊(RS)鋼殼內界面，內界面加載壓力瞬間達到約50 GPa，鋼殼聚心運動停止，開始向外反彈運動，其徑向厚度之后又逐漸減小，并向硅橡膠內反射沖擊波和向鋼殼內透射沖擊波，該反射沖擊波會再次聚心反彈加載，但已不在本算例時間內，而鋼殼內的透射沖擊波也會在內外界面上分解而交替產生壓縮波和稀疏波。

由從鋼殼內界面運動速度（見圖5）和加速度剖面（見圖6）看出，內界面首次受到沖擊加載后擾動開始反相（峰谷轉換），發生RM 不穩定性，接著又受到三次有效的向心反射壓縮波加載，在約12 μs 前，雖然有輕介質加速度重介質的RT 不穩定性，但以RM 不穩定性為主導。在12 μs 到沖擊波聚心反彈加載前，由于中心區域壓力的升高，界面聚心運動加速減速，擾動發展由輕介質加速重介質的RT 不穩定性主導。沖擊波聚心反彈加載后及之后內界面受到四次有效的向心反射稀疏波加載，擾動發展由RM 不穩定性主導。

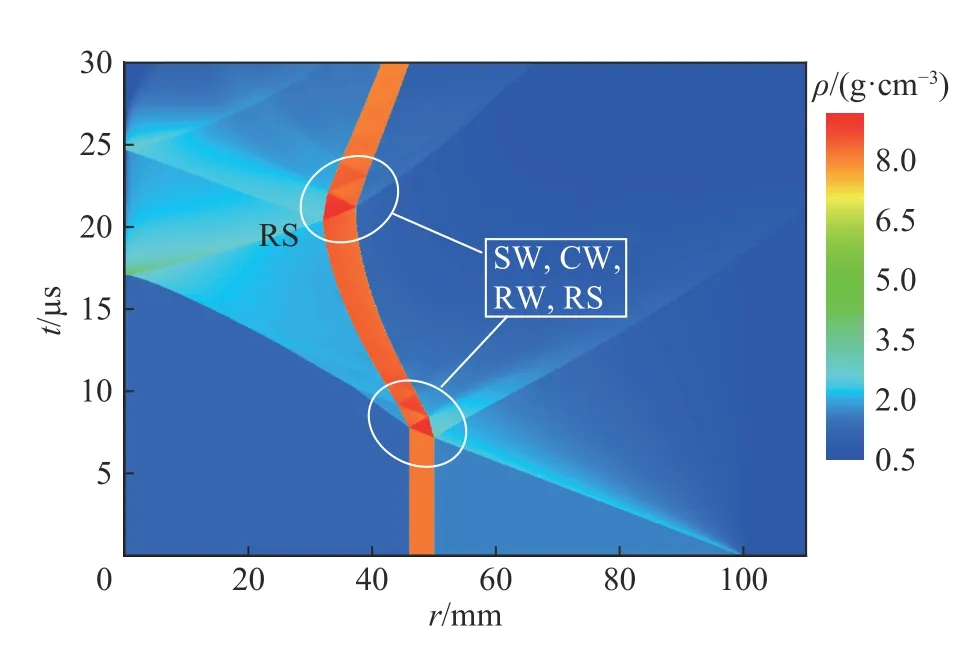
圖 3 密度顯示的一維波譜圖Fig. 3 One dimensional wave diagram displayed by density

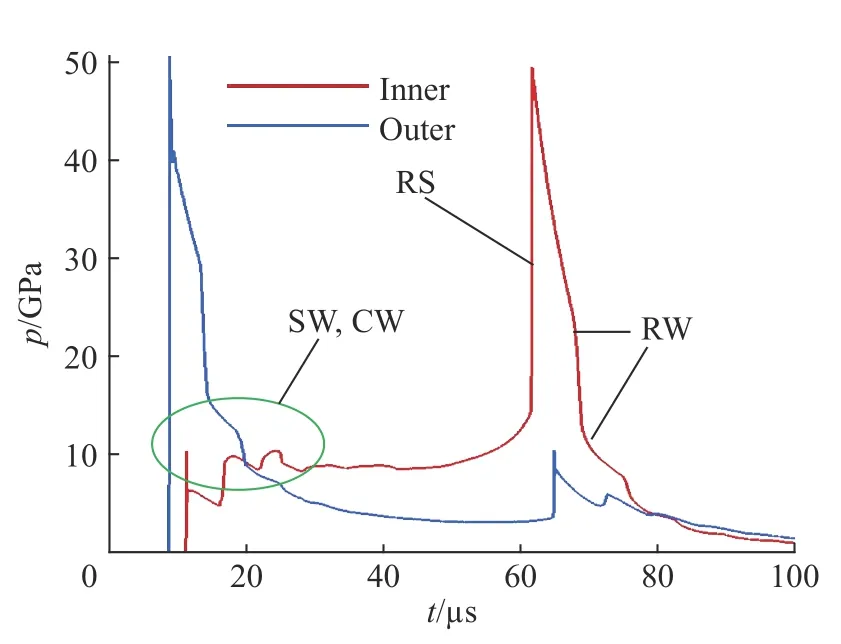
圖 4 不銹鋼殼內外界面加載壓力Fig. 4 Loading pressures on inner and outer interface

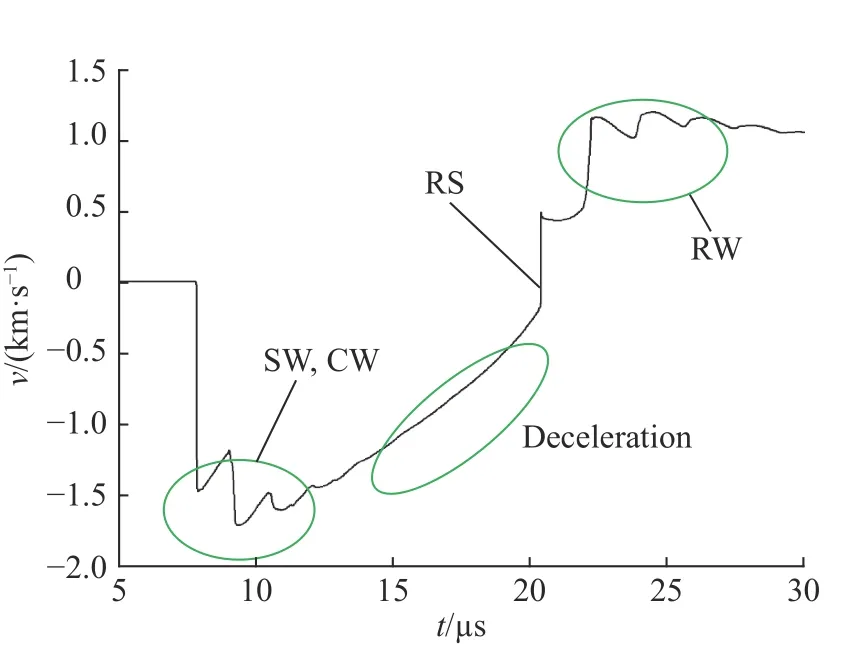
圖 5 不銹鋼殼內界面運動速度Fig. 5 Velocity of inner interface

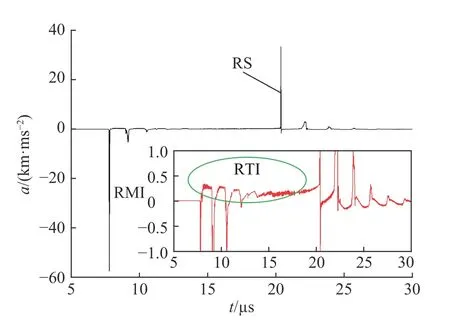
圖 6 不銹鋼殼內界面加速度Fig. 6 Acceleration of inner interface

2.3 擾動界面演化

圖7 為不同網格分辨率（146、73、36 μm）下鋼殼內界面雙模態擾動各模態（模數13 和29 mm?1）振幅增長過程，粗網格與中等網格、中等網格與細網格結果的最大相對誤差分別為3%、1.5%，滿足收斂要求，所以計算中采用36 μm 的網格。
圖8 為5、10、15、20、25 μs 時密度場圖像，顯示了鋼殼在內爆沖擊波和聚心反彈等加載下的運動過程和內界面擾動演化過程。圖9 為17.8、22.8 和25.3 μs 時鋼殼內界面擾動演化的實驗圖像和數值模擬圖像。圖10 為對雙模態擾動演化做譜分析得到的0、10、15、20、25 和30 μs時各模態的擾動振幅，在多次沖擊加載下，所有模態都被激發，但主導界面演化的還是模數13 和29 mm?1兩個模態。圖11 為雙模態擾動振幅增長歷史，數值模擬結果和實驗差別較大，原因是文獻[55]中并沒有說明內爆采用的是何種炸藥，而本模擬中采用TNT，TNT 爆炸后加載在鋼殼上的壓力和文獻[55]中的壓力有較大差別。由圖11 還可看出：低模數擾動增長比高模數擾動增長速度快，這與純流體情況剛好相反，是由金屬材料彈塑性機制導致；而且，對于低模數擾動，在擾動反相后至沖擊波聚心反彈加載前，擾動振幅以近似線性規律增長，而高模數擾動由于較強的非線性作用，非線性增長規律明顯。

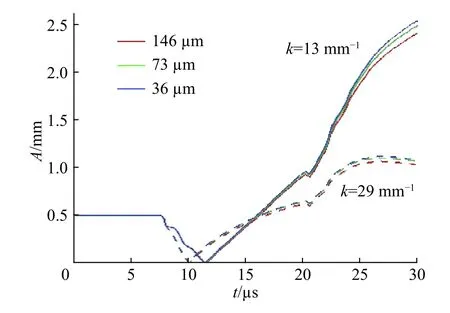
圖 7 網格收斂性分析Fig. 7 Grid convergence

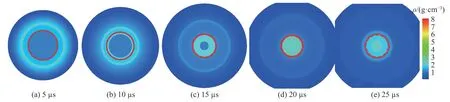
圖 8 密度場Fig. 8 Images of density fields

圖 9 鋼殼內界面的擾動Fig. 9 Inner perturbed interface of steel shell

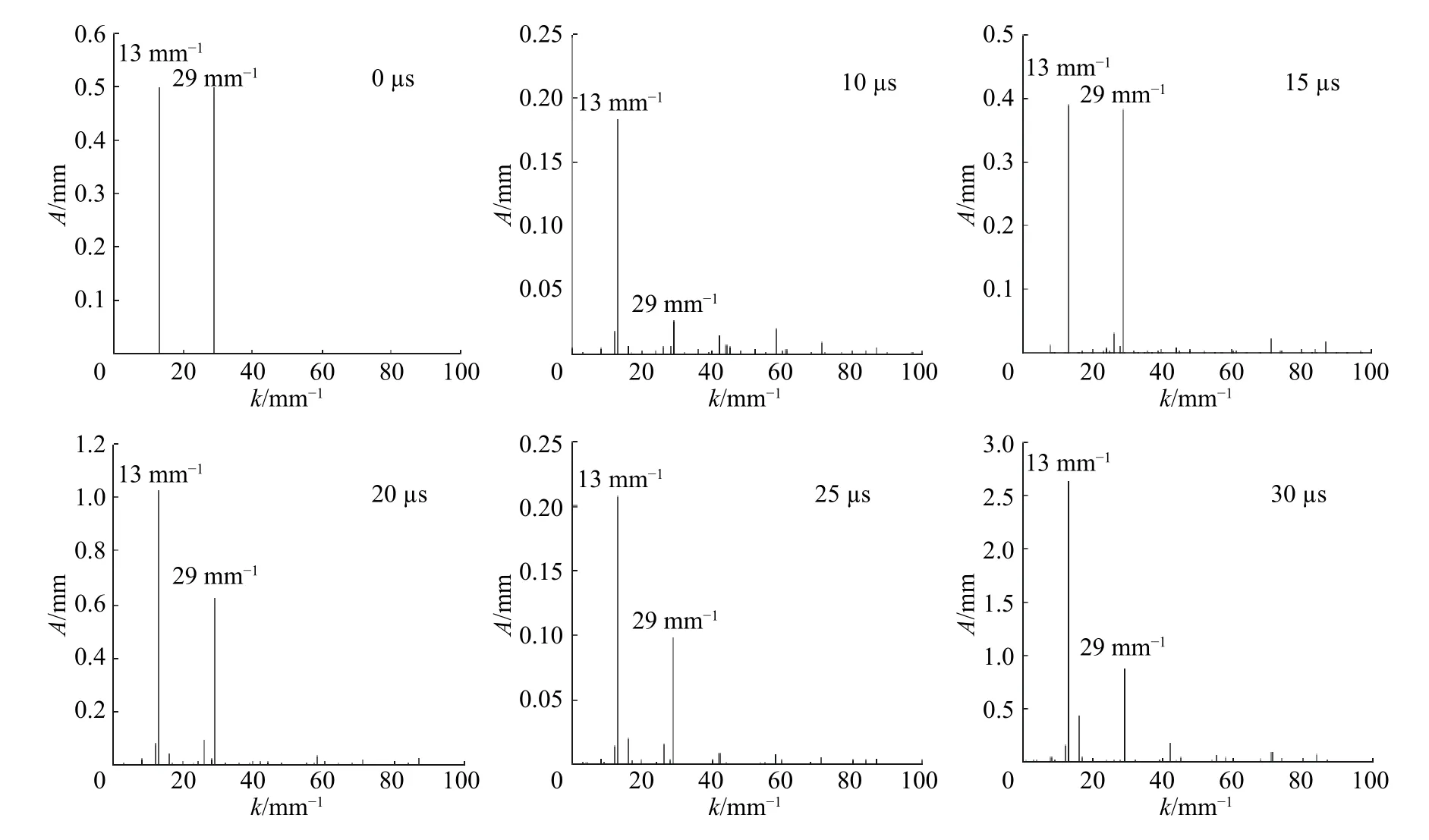
圖 10 雙模態擾動演化的譜分析Fig. 10 Spectral analysis of dual mode perturbation evolution

圖 11 雙模態擾動的振幅增長曲線Fig. 11 Amplitude growth curves of dual mode perturbation

2.4 初始擾動振幅、波長、鋼殼厚度和幾何特性的影響

本節主要研究初始擾動振幅、波長、鋼殼厚度和幾何特性對柱形內爆驅動下鋼殼內界面擾動增長的影響。

首先，研究初始擾動振幅的影響。保持初始擾動模數為13 mm?1，初始振幅分別為0.05、0.10、0.25、0.50、0.75 和1.00 mm。圖12 為不同初始擾動振幅時的振幅增長，較大的初始振幅意味著較大的振幅增長，而且擾動反相的時間與初始振幅無關。

其次，研究初始擾動波長的影響。保持初始振幅為0.5 mm，初始擾動的模數(波長的倒數)分別為13、16、20、24、29、35、40、45、50、56、60 mm?1。圖13 為不同初始擾動模數時的振幅增長，高模數（小波長）擾動反相時間明顯比低模數（大波長）擾動反相時間短，即擾動反相時間與擾動模數相關。反相后高模數擾動振幅增長速度比低模數擾動振幅增長速度快，但是低模數擾動振幅會以該速度近似線性增長，直至聚心反彈沖擊波加載時截止；而高模數擾動振幅增長速度會逐漸減小，其振幅及增長速度會小于低模數擾動；而且，隨著初始擾動模數的增大，振幅增長在后期會停止，說明柱形內爆驅動金屬材料界面不穩定性增長存在截止波長。

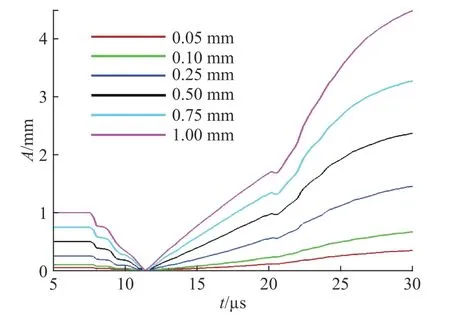
圖 12 不同初始擾動振幅時的振幅增長曲線Fig. 12 Amplitude growth curves for different initial perturbation amplitude

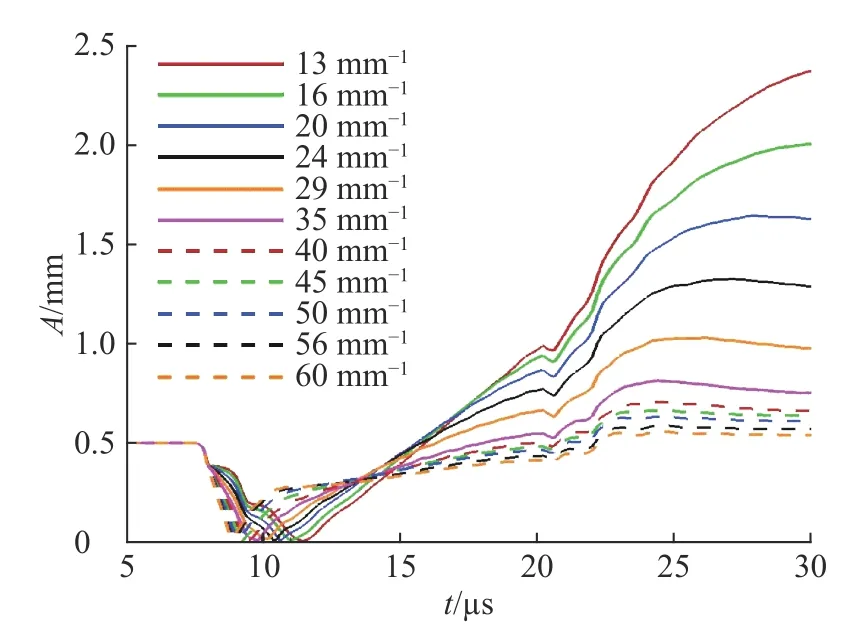
圖 13 不同初始擾動模數時的振幅增長曲線Fig. 13 Amplitude growth curves for different initial perturbation mode number

接著，研究鋼殼初始厚度的影響。初始擾動模數分13 和60 mm?1兩種，初始振幅均為0.5 mm，初始厚度分別為4、7 和10 mm。圖14 為不同鋼殼初始厚度時振幅增長情況：隨著鋼殼初始厚度的增大，擾動振幅增長速度逐漸減小；而且，對于模數為60 mm?1的初始擾動，不同厚度時的擾動振幅幾乎相同，后期增長也趨于停止，即鋼殼厚度會抑制擾動增長，而且存在一個截止厚度。

最后，研究幾何特性對沖擊驅動鋼殼界面不穩定性增長的影響。保持初始時刻的炸藥厚度、鋼殼厚度、硅橡膠厚度、擾動振幅和模數均相同的情況下，分為柱形匯聚幾何和平面幾何構型。初始振幅為0.5 mm，模數為13 mm?1。圖15 為不同幾何構型下的振幅增長情況，匯聚幾何構型下的擾動振幅比平面情況下大，這可以由兩種情況下界面運動速度(見圖16)和界面加速度(見圖17、6)解釋。首先，幾何匯聚帶來幾何收縮效應（BP 效應），由于能量匯聚使加載壓力較大，界面加速運動較快，因此擾動增長速度也較快；其次，當界面運動減速時，幾何收縮會造成界面加速減速，而平面情況下界面是減速減速，因此減速運動階段的RT 不穩定性發展在匯聚情況下更劇烈；再者，匯聚情況下沖擊波聚心反彈加載時間早于平面情況，而且反彈加載強度也較大，因此之后的RM 不穩定性發展在匯聚情況下也更劇烈。所以，整體上匯聚幾何中界面不穩定性發展速度快。

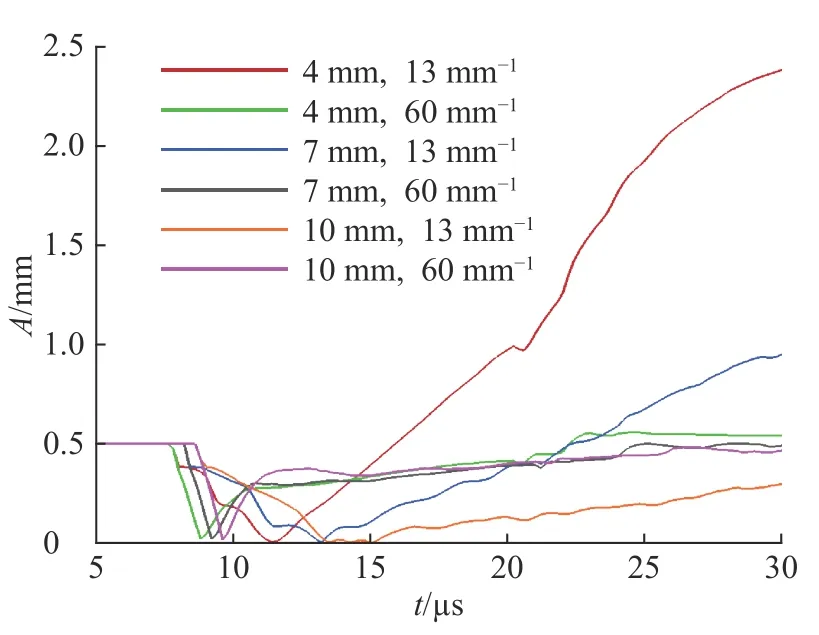
圖 14 不同鋼殼初始厚度時的振幅增長曲線Fig. 14 Amplitude growth curves for different initial thickness of steel shell

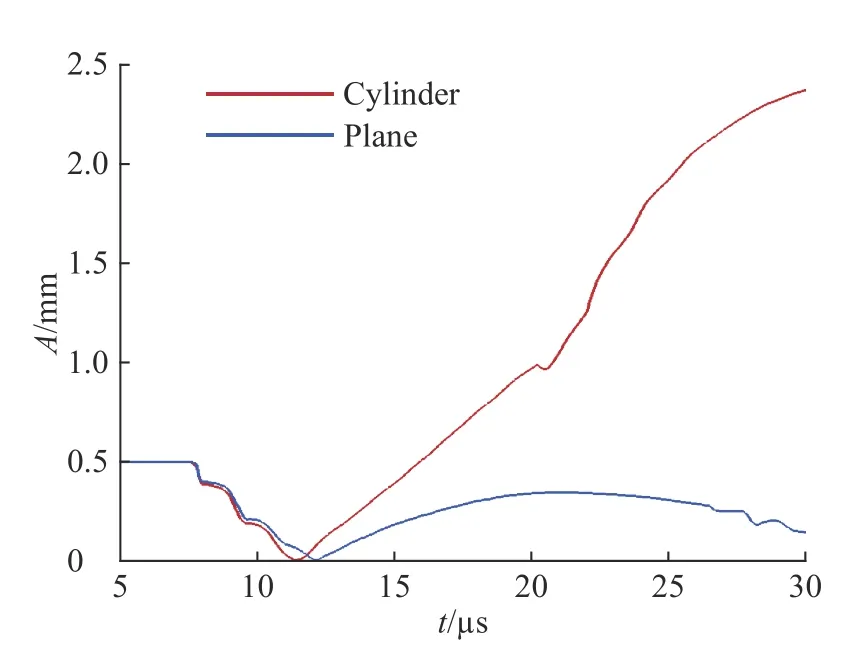
圖 15 不同幾何構型下的振幅增長曲線Fig. 15 Amplitude growth curves for different geometrical configuration

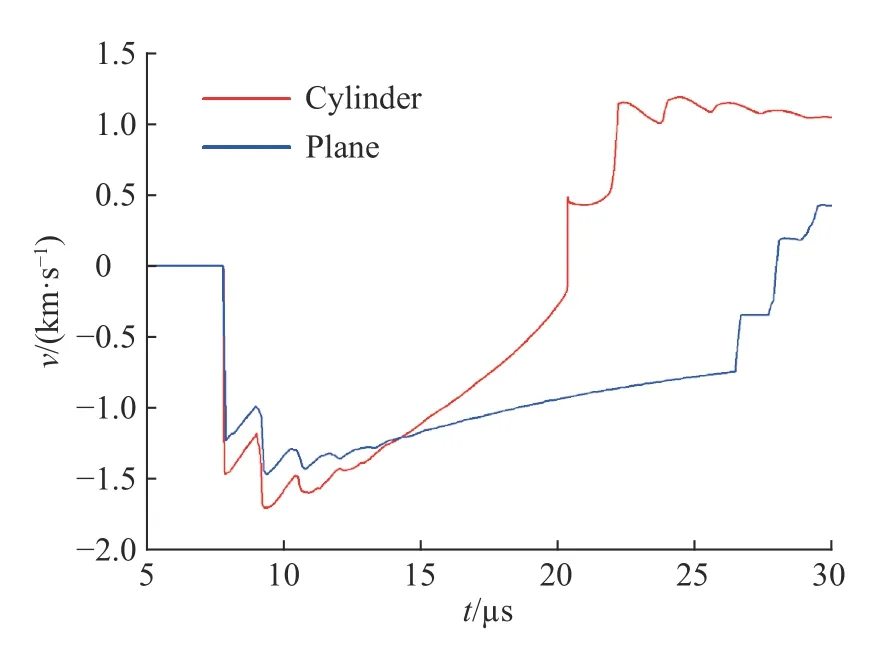
圖 16 不同幾何構型下的界面運動速度Fig. 16 Interface velocities for different geometrical configuration

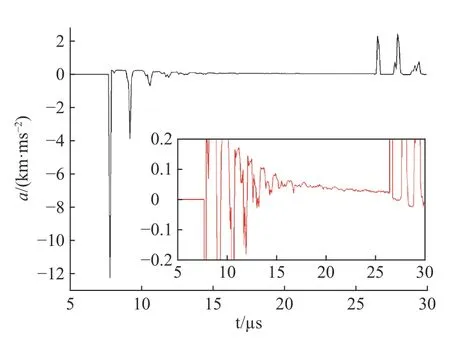
圖 17 平面幾何中的界面加速度Fig. 17 Accelerations of interface in planar geometry

3 結 論

基于歐拉有限體積法，發展了適用于多物質、大變形及強沖擊波條件下流體彈塑性問題數值模擬的高保真度爆轟與沖擊動力學計算程序。利用該數值模擬程序，研究了柱形匯聚幾何中內爆驅動下金屬材料界面不穩定性發展的動力學行為特征，得出以下結論。

（1）首次沖擊后，鋼殼開始聚心運動，在約12 μs 前，還受到了三次有效的向心反射壓縮波加載，在此階段，界面發展以RM 不穩定性為主；在12 μs 后到沖擊波聚心反彈加載之前，界面聚心運動處于一種加速減速狀態，界面發展由RT 不穩定性主導；在沖擊波聚心反彈加載后，界面又受到四次有效的向心反射稀疏波加載，此時界面發展又由RM 不穩定性主導。

（2）初始擾動振幅較大，振幅增長較大；初始擾動模數較大，振幅增長較小，且存在一個截止模數（波長）；鋼殼厚度會抑制擾動增長，也存在一個截止厚度；在相同初始條件下，相較于平面幾何構型，匯聚幾何結構中由于幾何收縮效應和界面減速階段較強的RT 不穩定性，使擾動增長速度更快。

金屬材料和流體最大的區別在于金屬材料的強度效應，而強度對擾動發展具有抑制作用。另外，由此帶來的材料斷裂破壞對擾動增長甚至混合都會產生影響，而且材料的斷裂破壞機制也復雜多變，其他如金屬材料的相變、微觀結構特征等，都會影響金屬材料界面不穩定性的發展，這都使金屬材料界面不穩定性問題更加復雜。下一步，我們擬研究材料強度對金屬材料界面不穩定性發展演化的影響，包括硬化、軟化等機制。