長桿彈撞擊陶瓷靶的一種數值模擬方法*

伍一順，陳小偉,2

（1. 北京理工大學爆炸科學與技術國家重點實驗室，北京 100081；2. 北京理工大學前沿交叉科學研究院，北京 100081）

長桿彈的長徑比(L/D)遠超過10，其彈體材料主要為高強度合金鋼、鎢合金和鈾合金(貧化鈾)，具有密度大、速度快、單位截面積上的動能高等特點，它常用于打擊各類防護裝甲。而陶瓷材料是一種經典的防護材料，它具有密度小、強度高、成本低等特點，是現代復合裝甲中不可或缺的一部分。

陶瓷材料廣泛用于裝甲的另一個重要原因是，陶瓷在抗長桿侵徹時會發生被稱為界面擊潰的特殊現象。界面擊潰是指當彈體撞擊速度低于某一速度值時，彈體在陶瓷表面徑向流動并發生質量侵蝕，同時速度下降，而陶瓷保持結構完整無明顯侵徹破壞[1]。20 世紀60 年代Wilkins[2]首先在實驗中觀察到這一特殊現象，90 年代Hauver 等[3]提出將該現象命名為界面擊潰。Rosenberg 等[4]研究了界面擊潰轉變為侵徹時的閾值速度，并定義其為轉變速度(transition velocity, TV)。

眾多學者在相關方向進行了大量的分析研究，也得到了許多重要的成果。Anderson 等[5]提出了描述駐留與界面擊潰的簡化理論模型。Lundberg 等通過大量實驗研究了鎢合金侵徹不同陶瓷材料產生的界面擊潰及界面擊潰轉侵徹[6-7]，研究了錐形彈頭的侵徹效應[8]、尺度效應[9]和預應力[10]對于界面擊潰的影響。Behner 等[11-12]設計一套實驗裝置來實現并記錄了細長金桿撞擊裸陶瓷靶及加有銅制緩存器的陶瓷靶。Anderson 等[13]進而開展了金桿斜撞擊陶瓷靶的實驗，研究不同傾斜度對應的界面擊潰的現象。Li 等對于界面擊潰轉侵徹進行了理論分析[14]，并比較了不同頭型[15]，不同角度侵徹[16]與正侵徹的區別。談夢婷等利用有限元軟件研究了長桿彈頭部形狀、蓋板、陶瓷預應力等對界面擊潰效應的影響規律[17]，并撰寫了陶瓷靶界面擊潰的綜述文章[18]。

近年來由于數值模擬的精確度和可靠性提高，許多學者開始采用數值模擬的方法來輔助實驗研究與理論推導。Holmquist 等[19]通過實驗數據擬合得到陶瓷的JH-1 模型，并用數值模擬的方法再現了長桿彈撞擊陶瓷存在界面擊潰現象。Quan 等[20]通過模擬得到與正侵徹實驗相一致的結果，并以此預測了斜侵徹產生的界面擊潰及駐留轉侵徹現象。談夢婷等[17]通過數值模擬再現了彈頭形狀對界面擊潰效應的影響，平頭、球形和錐形頭部長桿彈對應的轉變速度依次增加，還證明了增加陶瓷預應力可以提高轉變速度。Goh 等[21]模擬錐形長桿彈侵徹復合陶瓷靶板，模擬再現了增加背板的硬度可有效地增加駐留時間，但蓋板的硬度對于界面擊潰沒有影響。

但目前，有關長桿彈撞擊陶瓷裝甲產生界面擊潰的數值建模還較簡單，大部分算例都是長桿彈撞擊裸陶瓷靶，沒有考慮真實的彈體撞擊復合陶瓷裝甲工況。模擬較復雜界面擊潰的算例較少，且對于數值模型的前期建模及參數確定的介紹比較簡單。部分文獻忽視建模細節，導致其模擬結果和實驗結果不符。例如，在某些模擬結果中，蓋板在界面擊潰過程中整體彈出[20]，侵徹過程中彈頭形狀存在內凹現象[22]。為此，本文中將清晰介紹長桿侵徹陶瓷靶的數值計算方法，重點與實驗結果進行細節對比，完成模型可靠性的綜合驗證。

1 數值模擬方法

本文中以Lundberg 等[6]的鎢合金彈丸撞擊碳化硅陶瓷實驗為基礎，開展數值模擬復現實驗結果。AUTODYN 的無網格計算相對成熟，多數界面擊潰數值模擬采用AUTODYN 來計算，這里同樣采用AUTODYN 軟件進行二維建模計算。

1.1 數值算法及模型

根據Lundberg 等[6]的實驗裝置（圖1(a)）簡化得到長桿撞擊陶瓷靶板的幾何模型，建立如圖1(b)所示的二維軸對稱計算模型。在該模型中，彈體材料為鎢合金，長80 mm，半徑1 mm。蓋板與背板材料均為4340 鋼，厚8 mm，半徑為10 mm，兩板之間碳化硅陶瓷長20 mm，半徑10 mm。在復合靶板的外圍有厚4 mm 的MAR350 鋼管進行約束，其長度為36 mm。其中鎢合金桿和蓋/背板均采用SPH 算法，陶瓷靶板與約束管采用有限元的Lagrange 算法。SPH 粒子大小均為0.1 mm，有限元網格大小均為0.2 mm。具體算法以及網格(粒子)大小的選擇原因在下文中將進行詳細描述。

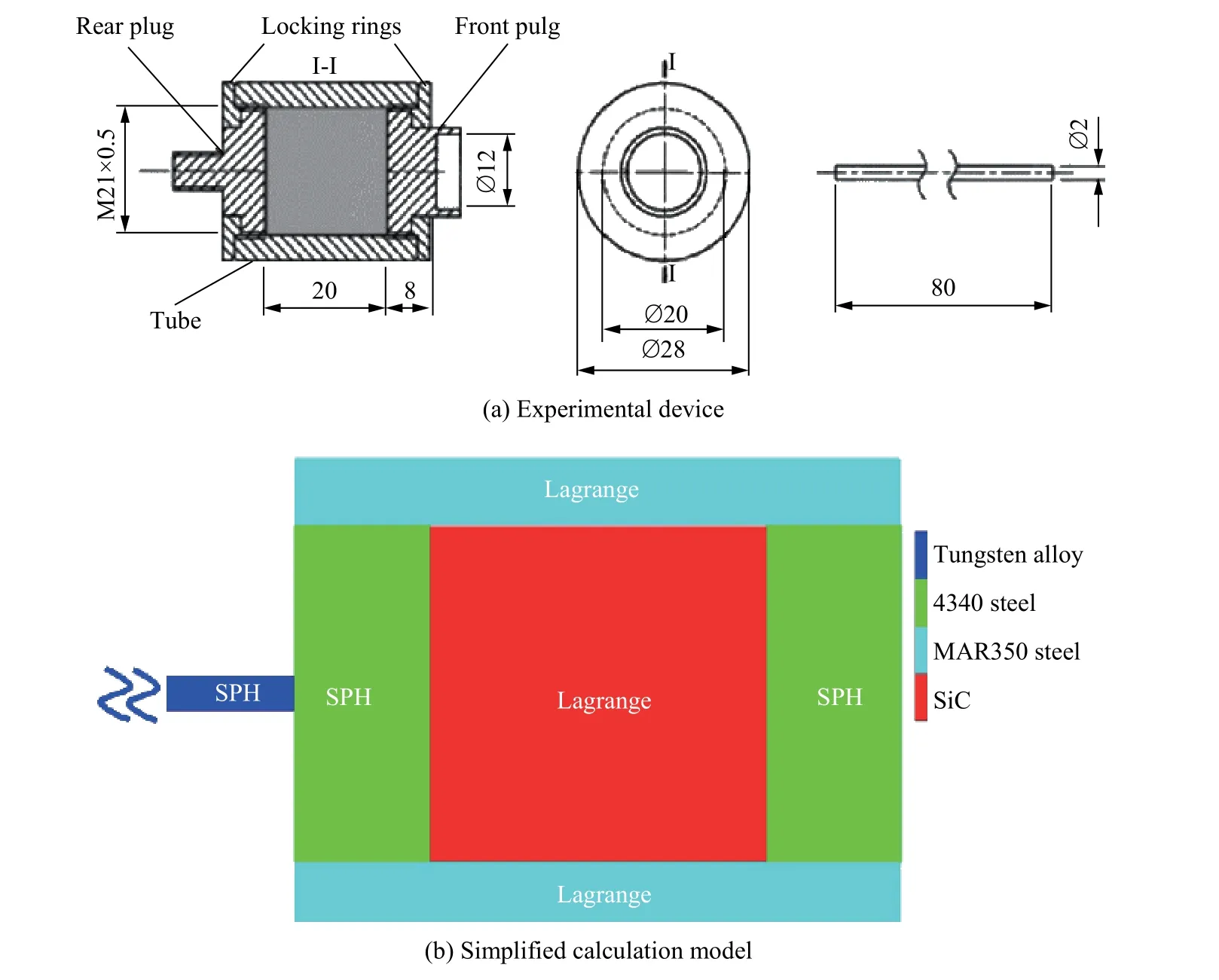
圖 1 實驗裝置和簡化計算模型(單位為mm)Fig. 1 The experimental device and the simplified calculation model (unit in mm)

1.2 材料模型及參數

JH-1 模型是Johnson 等[23]提出的描述脆性陶瓷材料的本構模型，它采用線性分段函數描述陶瓷材料的壓力強度關系、損傷和應變率效應。模型中各參數作用如圖2 所示。

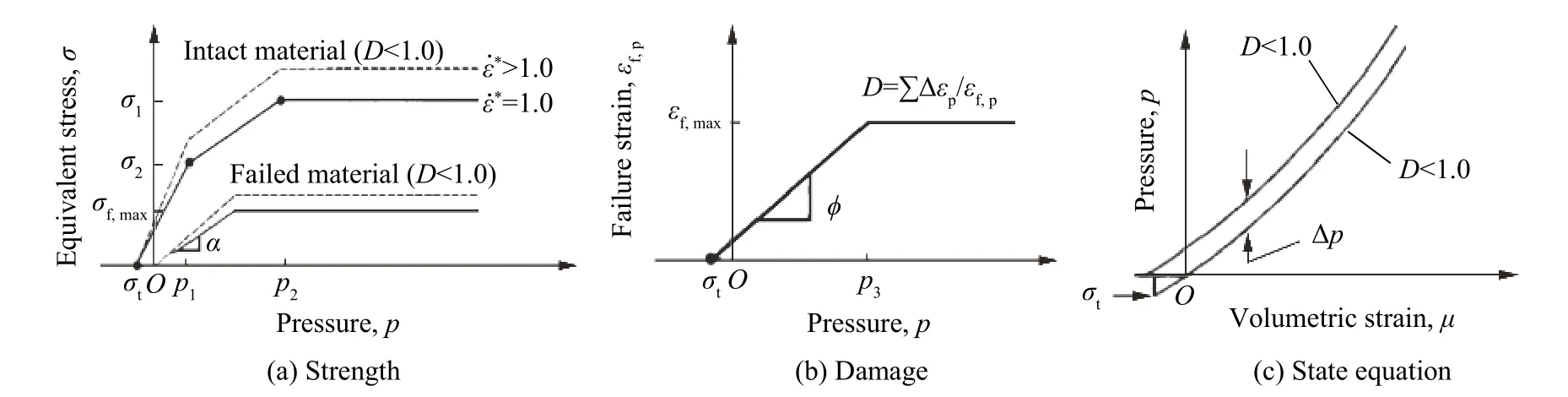
圖 2 JH-1 模型中應力、應變和壓力的關系[23]Fig. 2 The relations of stress and strain to pressure in the JH-1 model[23]

損傷參數D 的表達式為：

式中： ? εp為塑性應變增量， εf,p為壓力為p 時的失效塑性應變。在圖2(b)中，最大拉應力處不能產生失效塑性應變，由此與( p3,εf,max)確定斜率 ? =εf,max/(p3+σt) ，則 εf,p的表達式為：

當D＜1 時,狀態方程為多項式狀態方程，其表達式為：

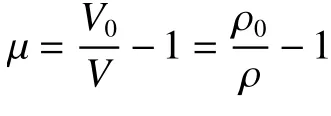
，其中V 為當前體積，V0為初始體積，ρ 為當前密度，ρ0為初始密度。

當D=1 時，體積開始膨脹并導致壓力和體積應變增加，膨脹效應可以用壓力增量 ? p 來體現，則式(4)變為：

文獻[19-20]表明，JH-1 模型對SiC 陶瓷材料的動態響應過程描述更合理，且模擬結果與實驗吻合程度高，所以本文采用JH-1 模型來描述SiC 陶瓷材料。

在AUTODYN 中，設置陶瓷的材料參數如表1 所示，表中T1為材料常數，σHEL為雨貢紐彈性極限，β 為膨脹系數，損傷系數 εf,max的值與Holmquist 等[19]取的1.2 不相同。損傷系數為計算參數，在計算中可以依據模擬結果進行適當修改，Quan 等[20]和Chi 等[22]的模擬計算中都對該項參數進行了調整。

表 1 碳化硅的材料參數[23]Table 1 Material parameters for SiC[23]

J-C 模型[24-25]將應變、應變率和溫度等影響因素表示為乘積關系，通過對相關參數的合理取值，能較好地描述金屬材料從準靜態到動態(高應變率)條件下的力學行為，相關表達式為：

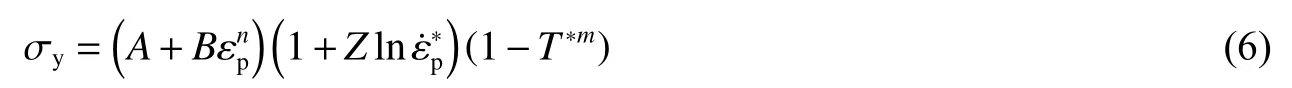
式中：σy為材料的屈服應力，A 為材料的準靜態屈服應力，B 為材料應變硬化模量；εp為有效塑性應變，為 歸 一 化 的 有 效 塑 性 應 變 率，= ε˙/ε˙0，ε ˙ 為 塑 性 應 變 率，ε ˙0為 臨 界 應 變 率；T*為 歸 一 化 的 溫 度，T?=(TP?T0)/(Tm?T0) ，TP、T0、Tm分別為材料變形過程的溫度、參考溫度和熔點溫度；Z 為應變率敏感系數，m 為溫度敏感系數，n 為應變硬化系數。

累積損傷模型通過定義損傷函數Dm來判定材料失效，其表達式為：

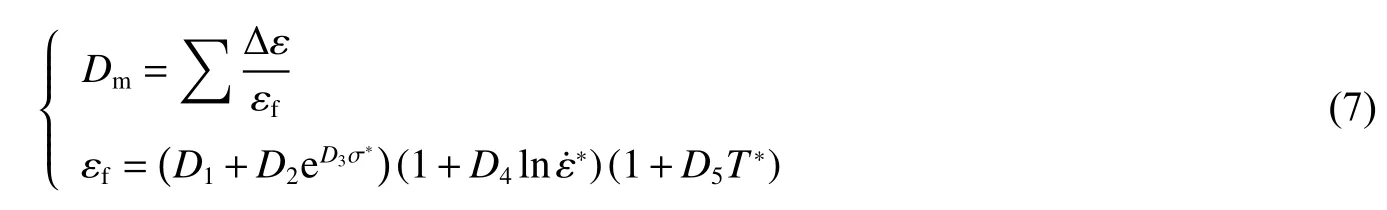
式中：損傷函數Dm的取值在0 到1 之間變化，當Dm=1 時材料失效，此時應力降為零；Δε 為等效塑性應變增量，εf為破壞應變，σ*為應力狀態參數，D1～D5為材料參數。

沖擊狀態方程是將沖擊過程的經驗公式 us=c0+supar代入Grüneisen 狀態方程，其表達式為：

式中：us為沖擊速度，upar為質點速度，s 為斜率系數，c0為當地聲速；p、pH分別為材料的壓力和雨貢紐極限處的壓力；E、EH分別為材料的比內能和雨貢紐極限處的比內能；γ 為Grüneisen 參數，V 為比容，cp為比定壓熱容。

鎢合金和4340 鋼均采用J-C 模型及沖擊狀態模型，其材料參數如表2 所示，本文中將具體討論不同鎢合金J-C 失效模型對于界面擊潰及侵徹的影響。M A R 3 5 0 鋼采用簡單的彈塑性模型，在AUTODYN 中，MAR350 鋼采用von Mises 強度模型和塑性應變失效模型。Von Mises 強度模型只需給出剪切模量G、屈服強度σy，塑性應變失效閾值εf設定為0.4，其模型參數如表3 所示。

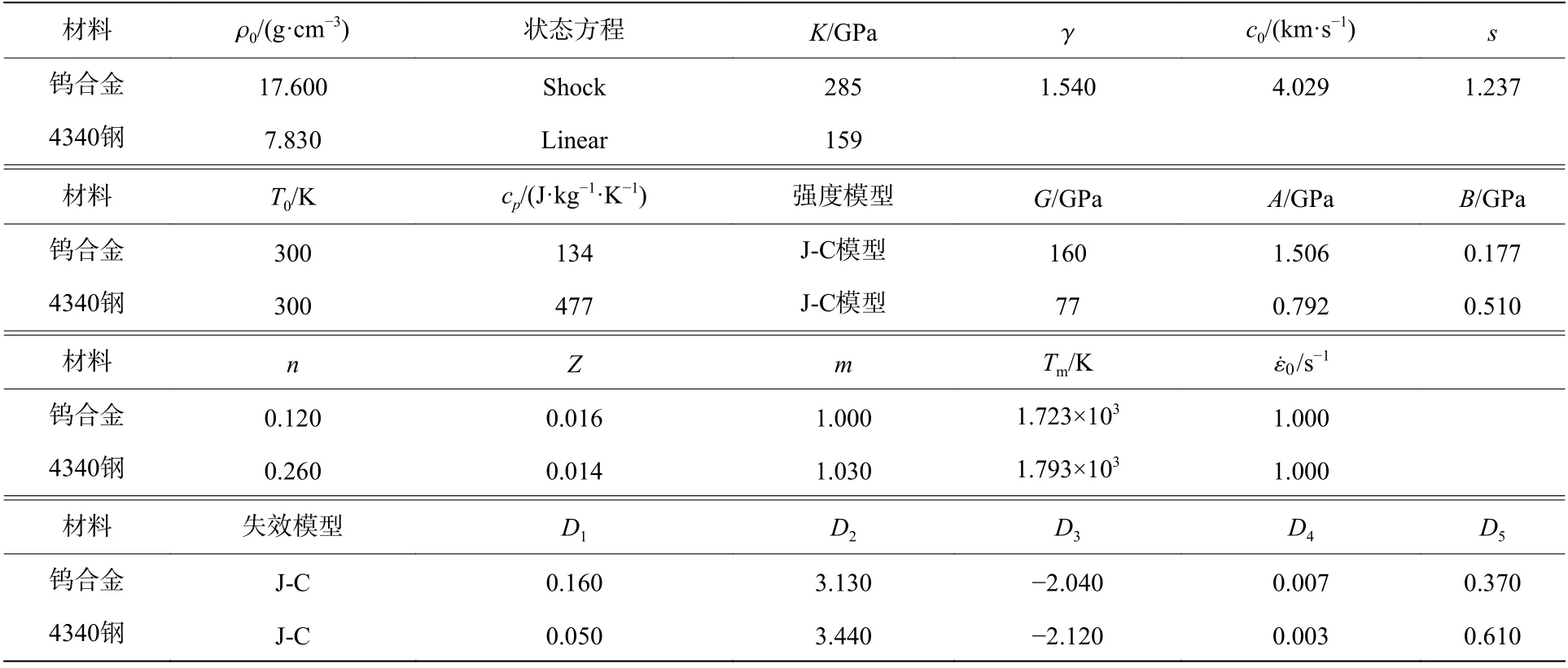
表 2 鎢合金和4340 鋼的材料參數[22, 26]Table 2 Material parameters for tungsten alloy and 4340 steel[22, 26]

表 3 MAR350 鋼的材料參數[20]Table 3 Material parameters for MAR350 steel[20]

1.3 邊界條件設置

在數值模擬中，通過研究實驗裝置的約束關系可以得到需要設定的邊界條件。本文選用的Lundberg 等[6]的實驗裝置如圖1(a)所示，在簡化得到幾何模型后，可以設定如下邊界條件：蓋板與背板均與約束管固連，陶瓷只與它們接觸而不固連，從而陶瓷可以在管內自由移動。

Quan 等[20]和Chi 等[22]的計算模型有類似的邊界設定，但計算結果都與實驗結果略有偏差。Quan 等[20]的計算結果中蓋板與約束管壁沒有固連導致在界面擊潰過程中蓋板稍有抬起。而Chi 等[22]的計算模型中蓋板與背板被嚴格固連在約束管上，陶瓷無法在管內運動，界面擊潰過程中失效粒子沒有足夠空間飛濺，導致粒子堆積影響計算的正確性。

為了獲得正確的蓋板邊界條件，設置了3 種不同邊界條件，分別為蓋板邊界全固連、邊界上半部分固連、邊界下半部分固連，如圖3 所示。通過比較3 種邊界條件的計算結果，得到最合適的邊界條件。

計算發現，圖3(a) 的計算發現失效粒子的飛濺范圍有限導致失效粒子堆積在彈頭侵徹區附近。圖3(b)中蓋板和背板在沖擊過程中能產生壓縮變形，失效粒子的運動區域足夠大從而不影響計算，并且蓋板前端約束也保證在侵徹過程中不會被抬起，較符合實驗結果。圖3(c)中蓋板受到向上的力，但下端被固連在固定的約束管上，導致在侵徹過程中會被拉斷，與實驗結果不符。原因可能是SPH 粒子失效后不會被刪除，如果將邊界完全約束，將沒有多余運動空間容納失效粒子，失效的鎢合金粒子和蓋板粒子會密集地堆積在一起，影響后續計算。而只約束蓋板前半部分，則不會造成該現象，并且實驗中鎖環的位置也在蓋板的前半部分，所以模擬也只約束前半部分。經過比較后決定，在蓋板的前半部分施加邊界條件，而保持后半部分自由，如圖3(b)所示。這樣的優點在于既約束了蓋板的運動，又保證陶瓷能在管內運動，失效粒子有足夠運動區域從而不會造成粒子堆積。同理，背板的處理應該與蓋板保持一致。

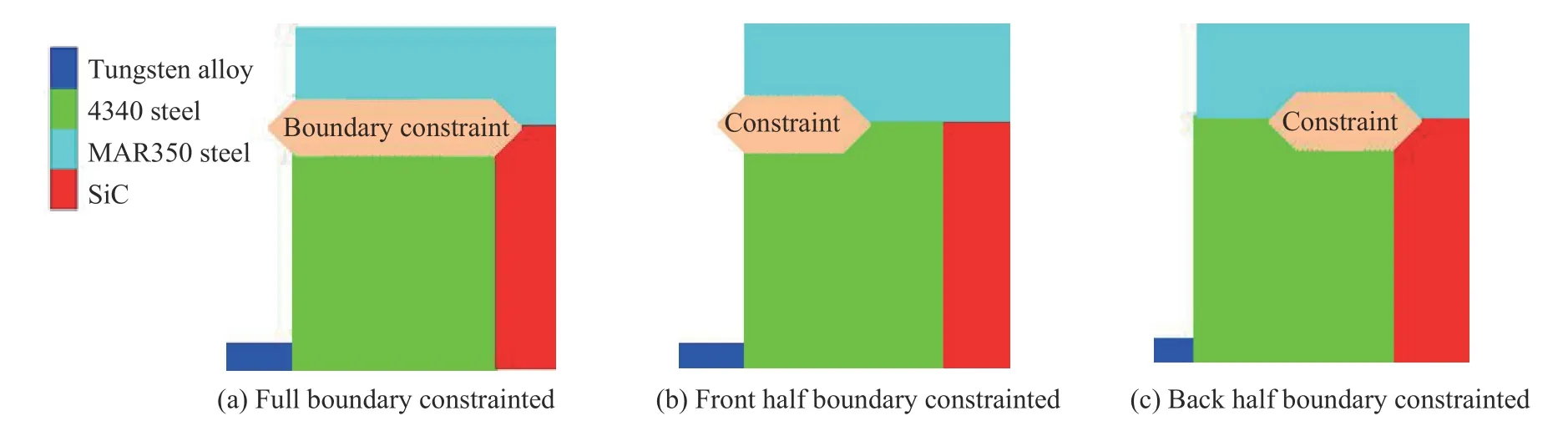
圖 3 邊界條件設置Fig. 3 Boundary condition settings

2 模型算法及網格收斂性

本文的計算模型是采用兩種算法混合計算，長桿彈和蓋板均采用SPH 算法計算，陶瓷靶采用有限元的Lagrange 算法計算。

光滑粒子流體動力方法(SPH)是將物體離散為一系列具有質量、速度和能量的粒子，然后通過核函數的積分進行估值，從而求得物體不同位置、不同時刻的各種動力學量。SPH 算法無需網格構建，又可保證連續體的結構精度，因此SPH 方法適用于模擬固體的破碎、層裂以及斷裂等大變形狀態。

在該模擬中為展現界面擊潰過程中彈體的徑向流動現象，長桿彈在侵徹過程中不能發生網格刪除，建議采用SPH 粒子建模。而其它兩個結構部件的算法選擇，將在下文進行詳細討論。在算法確定后，進行了網格收斂性的驗證，證明所選網格、粒子大小的合理性。

2.1 蓋板算法選擇

在侵徹實驗中，蓋板的作用是改變彈體頭型，減少沖擊載荷，增加彈與靶的作用時間，避免撞擊產生的拉伸應力導致靶板過快失效。在有關界面擊潰的模擬中，為避免蓋板與靶體的分界面處因網格刪除而導致壓力的驟失，在分界面周圍的蓋板單元都要用SPH 粒子建模而不能用Lagrange 網格建模。Chi 等[22]在文章中提出將蓋板均分為二，前半部分用Lagrange 算法建模，后半部分SPH 算法建模。該建模方法優點在于避免了碰撞開始時產生的網格大變形，同時又能保證分界面處不產生網格侵蝕。一般來說，一個部件分用兩種算法建模會存在物質的連續性以及能量的傳遞等問題，其計算準確性相較于單一建模略差。

圖4 是蓋板采用不同方法在同一時刻的結果比較。在侵徹過程中，兩者的彈頭都能保持蘑菇形，這與實驗結果觀察到鎢合金侵徹頭型一致。圖中左側兩種算法的交界面處能看到侵徹隧道的不連續且存在粒子堆積，而右側采用單一算法的侵徹隧道較光滑連續。但在彈體開坑處，右側蓋板存在撕裂現象而左側網格較正常，說明Lagrange網格確實能較好處理碰撞初期的網格大變形。但該算例研究重點在彈體形態變化，不關注初開坑處蓋板的撕裂情況。所以綜合比較兩種建模方法，全SPH 建模計算結果更符合模擬要求。同理為了保持模型的對稱性，背板的處理應與蓋板保持一致。

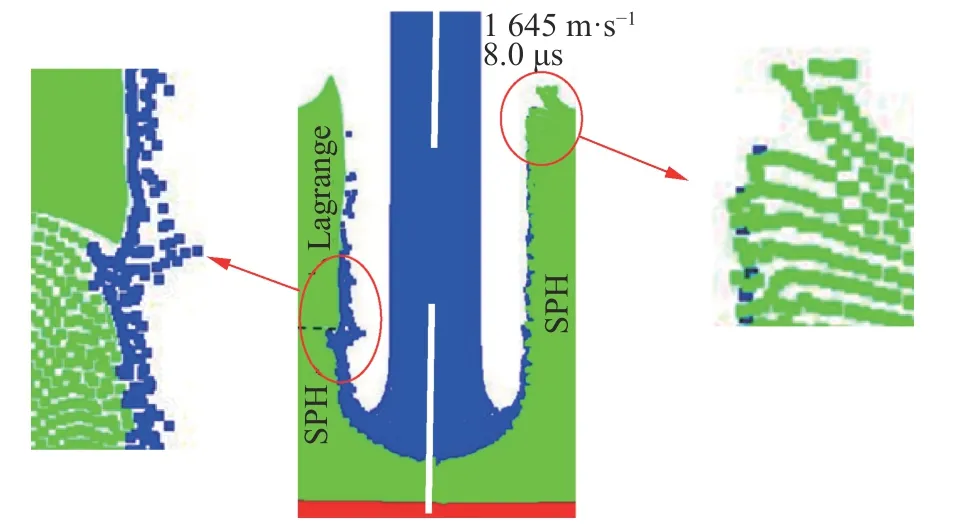
圖 4 蓋板模擬的兩種方案對應的模擬結果Fig. 4 Simulation results by two different schemes for cover plug modelling

2.2 陶瓷算法選擇

Lagrange 網格的優點是可以設置侵蝕參數，便于侵蝕計算。所以在已有的計算模型中，陶瓷材料基本都是采用Lagrange 有限元網格建模，而沒有采用SPH 粒子建模。為了探究兩種算法對于界面擊潰模擬的影響，本文擬對陶瓷分別采用Lagrange 網格和SPH 粒子建模，比較分析兩種算法對于陶瓷抗侵徹性能的影響。

以長桿彈以1 410 m/s 的速度侵蝕陶瓷靶板產生的界面擊潰現象為例進行計算。結果表明，采用粒子建模的模型無法產生界面擊潰現象，彈體直接開始侵徹陶瓷。分析陶瓷的損傷變化發現，在彈體到達陶瓷表面時，陶瓷內部已經產生了嚴重的損傷失效（圖5(a)），彈體直接侵徹陶瓷。所以陶瓷如果采用SPH 算法建模，其抗彈性能下降，將無法抵抗彈體侵徹。

采用Lagrange 網格建模的模型能夠正常產生界面擊潰現象直至侵蝕結束。彈體在到達陶瓷表面時，陶瓷內部尚未產生損傷失效（圖5(b)），且在接下來的撞擊過程中彈體能維持界面擊潰狀態。產生這種差別的原因可能是，當陶瓷類脆性材料采用SPH 粒子建模時，因SPH 粒子相較網格連接比較自由，當某處的壓力大于材料設定的壓力閾值時，內部粒子會發生移動，陶瓷材料則表現為發生損傷失效，結構無法保持的完整性，從而無法發生界面擊潰現象。所以在模擬界面擊潰時，為表征陶瓷材料優異的抗沖擊性能，陶瓷不建議采用SPH 粒子建模，應該采用Lagrange 網格建模。

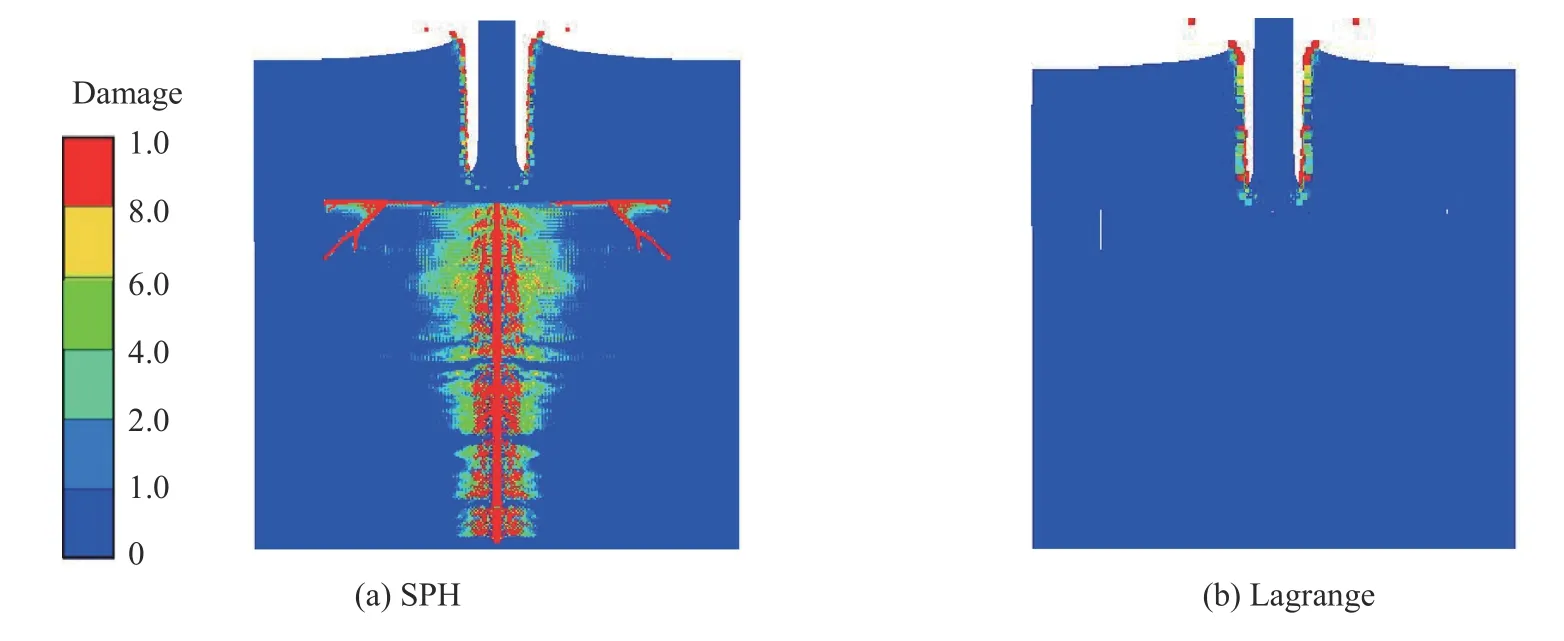
圖 5 陶瓷靶板采用不同算法建模計算結果Fig. 5 Simulation results of ceramic damage using different algorithm modelling

2.3 網格收斂性

為進一步確認計算結果的可靠性，還進行了網格收斂性測試。網格收斂性是指計算結果受網格大小變化的影響程度，一般認為網格密度越大，計算結果越準確。在本文的模擬中，網格尺寸需要通過經驗分析和計算驗證來確定。由于模型涉及2 種不同算法，還存在2 種算法之間網格和粒子大小匹配問題。

為確定網格大小以及網格匹配對于實驗結果的影響，以鎢合金桿1 410 m/s 撞擊陶瓷靶板產生的界面擊潰為例設計了9 組算例。為保證彈體半徑至少有8 個粒子，設定粒子大小分別為0.125、0.100、0.050 mm，同時設定Lagrange 網格和SPH 粒子的大小比值為0.5、1、2。按設定進行了9 組計算，模擬結果如表4 所示。

表 4 網格收斂性模擬結果Table 4 Simulation results of mesh convergence

僅當網格和粒子比值為2 時，不同的粒子大小均能使彈體保持界面擊潰現象，表明在該網格配比下，計算結果符合實驗結果，由此可以確定Lagrange 網格SPH 粒子大小的正確比值是2。

只觀察第3 列的結果還不能確定合適的SPH 粒子大小，還需結合不同粒子大小的計算結果來進行分析。通過比對第3 列3 個算例的計算結果，發現粒子越小，計算結果越細致，這與理論結果相一致。其中粒子大小0.100 mm 算例的計算結果基本符合實驗結果且明顯優于粒子大小0.125 mm 算例，與粒子大小0.050 mm 算例的結果基本相似。因此可以確定，當網格和粒子的大小繼續下降，其計算結果是收斂的。但如果將粒子大小由0.100 mm 減小到0.050 mm，其計算量要至少增加4 倍，計算難度大且實用性較差。所以綜合比較模擬結果與計算效率，確定Lagrange 網格大小0.200 mm，SPH 粒子大小0.100 mm符合模擬要求。

綜上所述，在已經確定了邊界條件，模型算法以和網格收斂性驗證后，基本可以模擬長桿彈以較低速度撞擊陶瓷靶板產生的界面擊潰現象。在后續計算中，若提高長桿彈的撞擊速度至轉變速度或者遠高于轉變速度，還需驗證相應模型結果是否和實驗結果相一致。

3 模擬參數驗證

已有文獻關于長桿撞擊陶瓷靶的二維模擬，其彈頭形狀通常會呈現中間內凹的形狀（圖6(a)），這與實驗結果不一致。我們認為：鎢合金的失效模型和陶瓷的侵蝕參數是影響侵徹過程中彈頭形狀的主要因素。

3.1 材料參數選擇

在相關的模擬計算中，彈體鎢合金材料大部分采用J-C 模型，部分采用彈塑性模型。Chi 等[22]與談夢婷等[17]的模擬均參考Lee[27]文章中的J-C 模型參數，Quan 等[20]給出簡單的彈塑性模型參數，兩種模型雖然不同但在計算過程中都存在問題。簡單彈塑性模型參數簡單，但在涉及到材料失效和破壞時，其計算結果和實驗有較大出入。

采用Lee 的J-C 失效模型參數的彈體在侵徹陶瓷時，鎢合金侵徹頭型總是不呈現蘑菇形。圖6(a)是Chi 等[22]的計算結果，從彈頭放大圖可以看到彈頭形狀存在奇異。圖6(b)是作者采用相同參數計算得到的結果，彈頭損傷放大圖顯示彈頭部分損傷明顯。分析發現，其可能原因是彈材失效模型太弱而導致彈頭形狀奇異。因此，文獻給出的兩種模型參數都不合適，需要對J-C 模型中的失效模型進行修正。

圖 6 長桿侵徹陶瓷靶模擬圖和彈頭放大圖Fig. 6 Simulated penetration of a long rod into a ceramic target as well as the magnified view of the projectile nose

失效模型是用來表征材料的斷裂特性，其作用是強度模型和狀態方程無法替代的。表5 是Lee[27]的J-C 失效模型參數和修正的J-C 失效模型材料參數，其中修正模型來自郎林等[26]給出的鎢合金J-C 失效模型。2 套材料參數中密度，楊氏模量和屈服強度等參量均相同，只有失效模型不同，因此2 個模擬中的鎢合金應為同一種材料。為確定修正失效模型的優異性，設計算例1～3，分別表示鎢合金采用無失效模型、Lee 的J-C 失效模型和修正J-C 失效模型。其中彈體撞擊速度為1 410 m/s，3 個算例結果如圖7 所示。

表 5 J-C 失效模型參數[26-27]Table 5 Damage parameters in the J-C models[26-27]

算例1 中鎢合金彈丸無法在陶瓷表面產生徑向流動(圖7(a))，因為鎢合金材料無法斷裂而導致彈體粒子在陶瓷表面沿一定角度飛濺，這會導致飛濺點處應力集中而提前損傷破壞，陶瓷完整性破壞而導致無法保持界面擊潰狀態。

算例2 和算例3 中鎢合金彈能順利在陶瓷表面展開，并保持界面擊潰狀態，但同一時刻彈體界面擊潰展開面積不同。材料的失效模型越弱，彈體越容易發生破壞，失效粒子越多從而在陶瓷表面流動的速度加快。將算例3 的陶瓷損傷圖與實驗結果進行比較，如圖7(b)～(c)所示，桿彈在達到陶瓷表面后，在彈體的正下方出現一個明顯的損傷區域，并且在應力集中處出現了錐裂紋，這與實驗結果是相吻合的。

上述3 個算例證明了鎢合金彈體采用J-C 失效模型能模擬界面擊潰現象，但還需要驗證采用修正JC 失效模型的彈體在侵徹過程中頭部是否出現明顯的內凹現象。設置彈體撞擊速度遠高于轉變速度，從而彈體能直接侵徹陶瓷靶板。圖8 給出相同特征時刻的侵徹圖和頭部損傷圖，顯然，在侵徹過程中彈頭是典型的蘑菇形。從圖8(b)的損傷圖可知彈頭部分的損傷失效較圖6(b)要小，所以采用原失效模型，鎢合金彈體易失效，彈頭無法在侵徹過程中呈現蘑菇形。

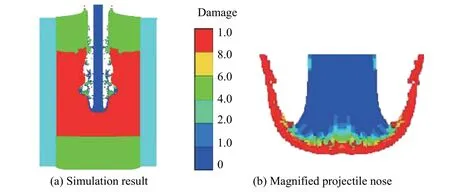
圖 8 采用修正J-C 失效模型的模擬結果和彈頭放大圖Fig. 8 Simulation result using the J-C modified model and the magnified view of the projectile nose

綜合界面擊潰以及侵徹的模擬結果，算例3 更符合實際實驗結果，在接下來的模擬中將采用修正JC 的失效模型進行計算仿真。

3.2 侵蝕參數選擇

采用侵蝕算法是處理侵徹問題的一種常用的手段。在本文的模擬中，被侵徹的陶瓷靶板采用Lagrange 網格建模，采用塑性應變侵蝕能較好處理網格的變形與刪除，但侵蝕參數大小會影響侵徹過程中彈頭形狀。在討論鎢合金的失效模型時已表明，若彈體材料越容易損傷失效，則計算中網格刪除的影響越大。通過設置不同閾值進行計算發現：侵蝕閾值越小，彈頭形狀越光滑；而侵蝕閾值越大，網格越不容易刪除，從而網格變形越大，四邊形網格甚至可能退化為三角形網格，彈頭形狀越尖銳。因此，閾值大小也會影響侵徹過程中的彈頭形狀。

塑性應變侵蝕閾值不僅與網格變形有關，還與侵徹深度密切相關，而與侵徹深度有關的另一個參數就是陶瓷損傷系數 εf,max。通過單一變量控制計算發現， εf,max的大小能夠影響駐留時間，增加 εf,max值能明顯延長彈體駐留時間，同時減小侵徹深度。而塑性應變侵蝕閾值不會影響駐留時間，但增大閾值會減小侵徹深度。

圖 9 不同撞擊速度下在SiC 靶中的侵徹深度Fig. 9 Depth of penetration (DOP) into SiC targets at different impact velocities

雖然2 個變量都會影響侵徹深度，但2 個計算變量并非耦合，可以通過解耦來分別確定2 個變量的大小。可以通過先擬合駐留時間確定εf,max的大小，再通過侵深-時間曲線確定塑性應變侵蝕閾值大小，如此可以達到近似解耦的效果。本文以鎢合金彈以1 645 m/s 撞擊陶瓷靶板為例來確定2 個參數大小，結果得到 εf,max=0.6，塑性應變侵蝕閾值為1.7 時，侵蝕深度最接近實驗結果(圖9），且此時彈頭形狀能保持良好。

4 模擬結果

按照上述確定的計算模型模擬鎢合金桿彈以1 410、1 645、2 175 m/s 的特征速度撞擊陶瓷靶板，這3 個速度分別對應鎢合金桿彈界面擊潰、駐留轉侵徹以及直接侵徹。

鎢合金桿彈以1 410 m/s 的速度（低于轉變速度）撞擊陶瓷靶板，時間歷程如圖10(a)所示。彈體在達到陶瓷表面后在陶瓷表面徑向流動，而陶瓷材料不發生明顯損傷。圖10(b)是界面擊潰末期的結果圖，可以看到彈體能始終保持界面擊潰狀態，直至彈體失去速度，最終侵蝕結束。

鎢合金桿彈以1 645 m/s 的速度（略高于轉變速度）撞擊陶瓷靶板，時間歷程如圖11(a)所示。長桿彈在擊穿蓋板后，先在陶瓷表面徑向流動，駐留約6 μs 后開始侵徹陶瓷靶板。所以駐留轉侵徹的物理過程即為彈體先在陶瓷駐留，陶瓷損傷區域不斷擴大直到無法抵抗彈體侵徹，彈體開始侵徹靶板。圖11(b)是侵徹末期的結果圖，彈體還存在剩余速度，最終彈體會擊穿靶板。

鎢合金桿彈以2 175 m/s 的速度（遠高于轉變速度）撞擊陶瓷靶板，時間歷程見圖12(a)，桿彈還未到達陶瓷界面時，陶瓷已經發生壓縮變形。所以當桿彈到達陶瓷表面后，陶瓷靶板無法抵抗彈體侵徹，彈體直接侵徹陶瓷靶。圖12(b)是侵徹末期的結果，該速度下彈體對陶瓷的破壞效果顯著。

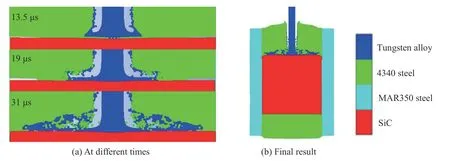
圖 10 界面擊潰模擬結果Fig. 10 Simulated interface defeat

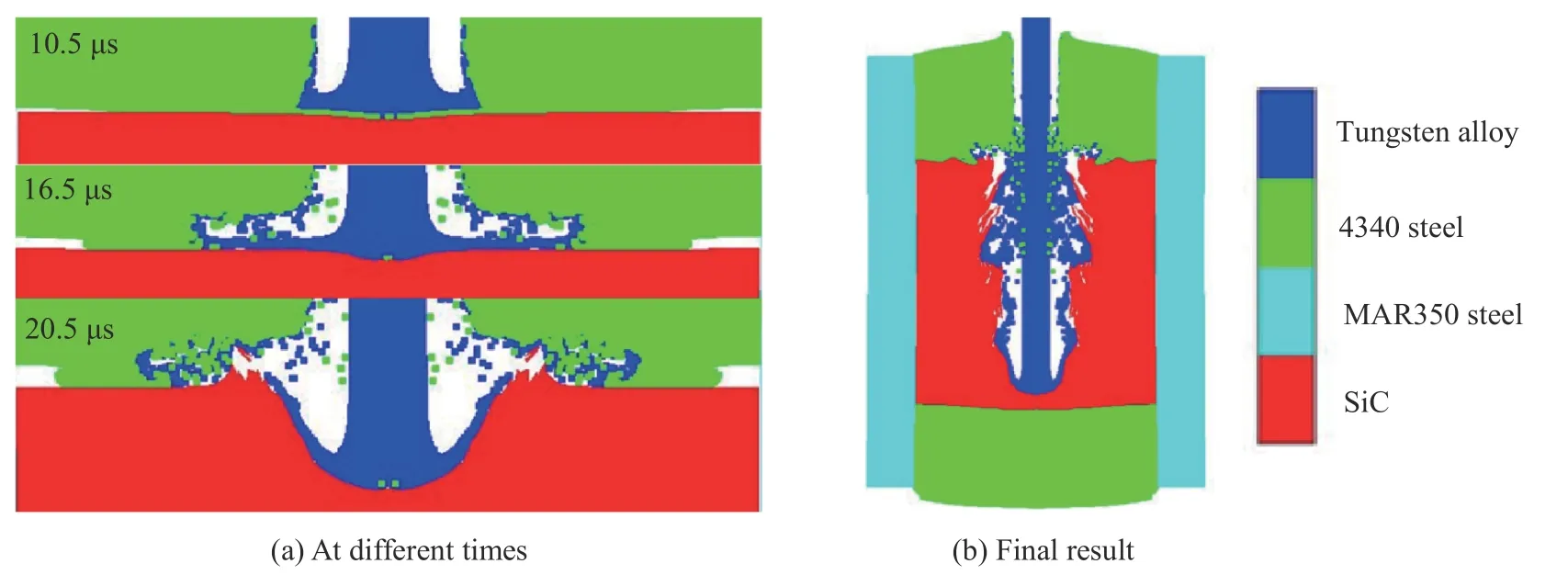
圖 11 駐留轉侵徹模擬結果Fig. 11 Simulated transition from dwell to penetration

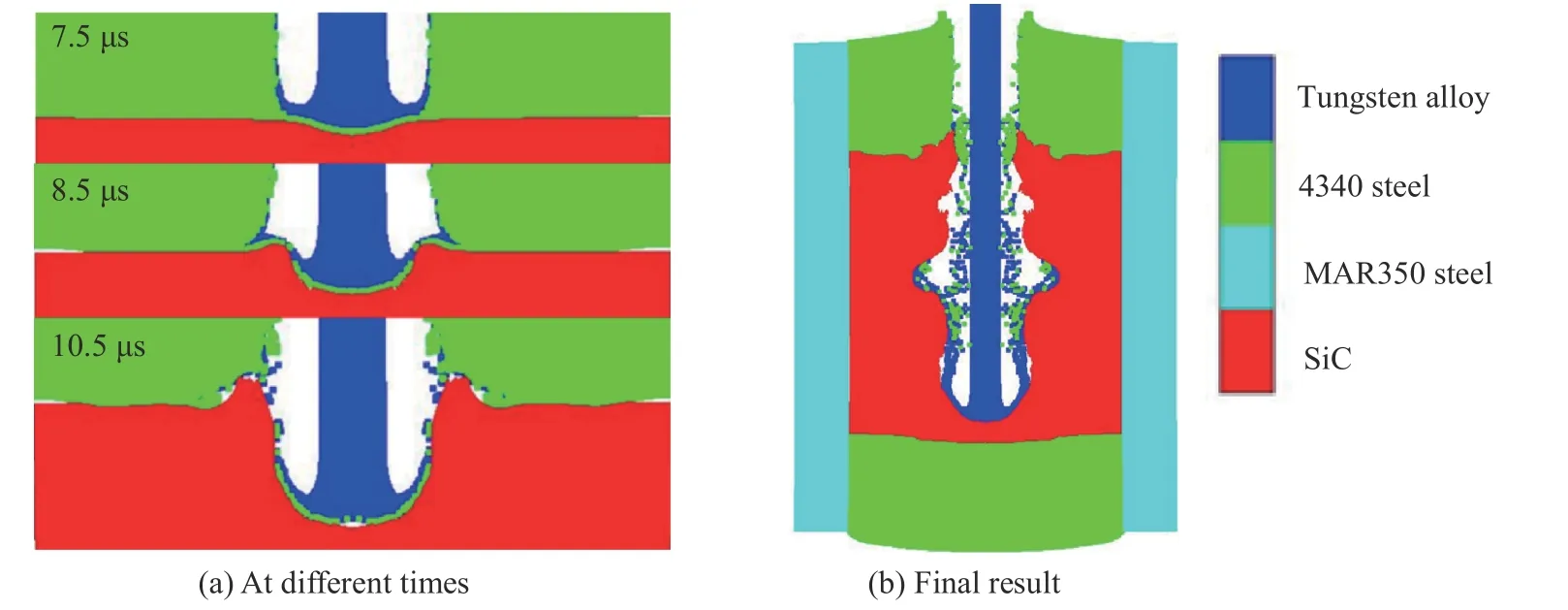
圖 12 直接侵徹模擬結果Fig. 12 Simulated direct penetration

5 結 論

采用AUTODYN 軟件模擬了不同速度的長桿彈撞擊陶瓷靶板發生的界面擊潰、駐留轉侵徹以及直接侵徹現象。研究重點在于模型的建立以及可靠性驗證，通過對某些特殊參數進行修正使得計算結果更加符合實驗結果。在模型建立過程中，通過反復調整驗證得到以下結論。

（1）在模擬中若同時使用SPH 算法與Lagrange 算法，需要考慮粒子與網格大小的影響。在計算中，SPH 粒子大小和Lagrange 網格比例建議設為1∶2 時較合適。

（2）模擬長桿彈侵徹陶瓷靶板產生界面擊潰時，陶瓷材料不建議采用SPH 粒子建模，并且鎢合金失效模型需要修正，其計算結果更接近實驗結果。

（3）陶瓷損傷系數 εf,max影響駐留時間以及侵徹深度，而侵蝕閾值只影響侵徹深度。先通過擬合駐留時間確定 εf,max大小，再通過擬合侵徹深度確定侵蝕閾值，能夠達到參數解耦的作用。