色噪聲驅動下的隨機共振現象

張 珍，宋群群，楊會靜

物理科學與技術

色噪聲驅動下的隨機共振現象

張 珍，宋群群，楊會靜

（唐山師范學院 物理系，河北 唐山 063000）

研究了一維雙勢阱中布朗粒子的動力學行為。模擬結果表明，布朗粒子在一維雙勢阱中存在隨機共振現象。當色噪聲強度為某個合適值時，布朗粒子的時間相干性達到最佳水平，色噪聲的自相關時間會影響布朗粒子隨周期信號的同步行為。

隨機共振；色噪聲；Q因子；關聯時間

自然界中，白噪聲是不存在的，由于其產生需要無窮大的功率，而噪聲總是有一定時間關聯的，只有噪聲的關聯時間遠小于體系的馳豫時間時，噪聲的關聯才可以忽略，作為白噪聲來處理。但是通常情況下，噪聲的關聯時間是比較長的，因此研究具有非零時間關聯的色噪聲對隨機系統的影響更有實際意義[1-4]。隨機共振最早是由Benzi[5]等人在研究古氣象冰川問題時提出的。近年來，人們對隨機共振進行了大量的研究，所涉及的學科包括物理、化學、生物以及生物醫學[6-9]等。探究布朗粒子在如圖1所示的一維雙勢阱中的動力學行為并假定布朗粒子在水平方向受到周期力和隨機力的共同作用。通過大量數值模擬，發現當施加的色噪聲強度合適時，可以觀察到隨機共振現象。另外，我們發現色噪聲的自相關時間也會影響布朗粒子的動力學行為。

1 模型與方法

圖1 布朗粒子在一維雙勢阱中運動的示意圖

一維雙勢阱的形狀可以通過下面的方程進行描述

(1)

其中，()決定了一維雙勢阱受限空間的大小。布朗粒子在運動過程中受到周期力和隨機力的共同作用，那么該布朗粒子的動力學行為可以通過過阻尼的朗之萬動力學方程描述

其中，()代表布朗粒子受到水平方向的周期力，形式為

2 結果與討論

圖2 布朗粒子質心x(t)的時間序列圖

圖2給出了不同噪聲強度下，布朗粒子隨時間的演化情況。從圖中可以看到，當噪聲很弱時，我們觀察到布朗粒子的跨越勢壘的事件很少。當噪聲很強時，雖然觀察到布朗粒子跨越勢壘事件很多，但是比較混亂。當噪聲強度比較合適，即=0.6時，布朗粒子跨越勢壘往返的頻率幾乎與所施加的周期外力的頻率一致。這些性質都是隨機共振現象的特性。為定性地說明隨機共振現象，計算了在不同噪聲強度下的因子[10-12]。因子可以衡量隨機共振的強弱，它的定義形式如下：

其中，t代表該體系的模擬時間，通常情況下我們要求模擬時間要足夠長。

從圖3可以觀察到，在每一個頻率下，因子都會出現一個極大值。在峰值的左側，因子隨著噪聲強度的增大而增大，但是當噪聲強度增大到一定值時，因子的值反而會有所下降，所以隨機共振的強弱受噪聲強度大小的影響。只有噪聲強度合適時，才會出現隨機共振現象。在同樣的噪聲強度下，隨著周期力頻率的增大，因子的值會減小，并在峰值處減小的幅度是最大的。在各頻率下，因子隨著噪聲強度的增大而減小，并且會趨向一個極小值。所以可以推斷，當頻率較小時，會加強系統對信號的響應，布朗粒子的隨機共振現象會增強。

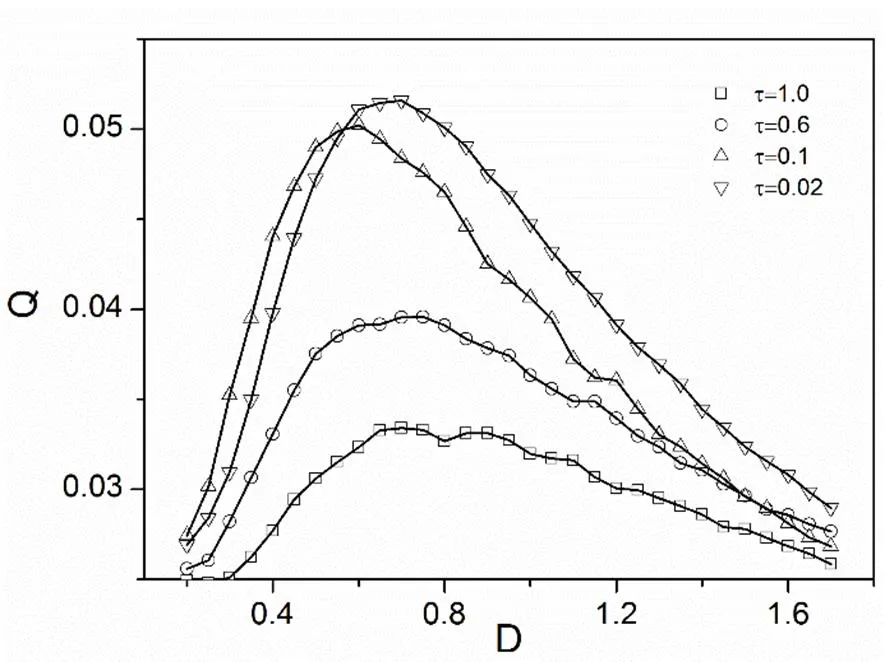
圖4 Q因子隨著色噪聲強度的變化

圖5 不同噪聲強度下，Q因子隨關聯時間t的變化

3 結論

本文主要考察了色噪聲對布朗粒子動力學行為的影響。研究結果表明，當施加的色噪聲強度合適時，布朗粒子會從一個勢阱中跨越勢壘而運動到另一個勢阱中做來回運動，并且布朗粒子的穿越行為會隨著外信號的變化表現出很好的相干性。此外，我們還研究了不同頻率以及關聯時間下，因子隨噪聲強度變化的關系。同時考察了在不同噪聲強度下，因子對關聯時間的依賴關系，這些因素都會對布朗粒子的隨機共振行為產生一定的影響。本文的研究工作可加深我們對隨機共振現象的理解與認識。

[1] 李玲,謝征微.色噪聲驅動的布朗粒子在周期勢場中的運動[J].四川師范大學學報,1996,(4):80-84.

[2] 張曉燕,徐偉,周丙常.色高斯噪聲驅動雙穩系統的多重隨機共振研究[J].物理學報,2011,(6):162-167.

[3] 周玉榮,郭鋒,蔣世奇,等.色噪聲作用下線性系統的隨機共振[J].電子科技大學學報,2008,(2):232-234.

[4] Dimian M, Manu Q, Andrei P. Influence of noise color on stochastic resonance in hysteretic systems[J]. Journal of Applied Physics, 2012, (111): 07D132.

[5] Benzi R, Sutera A, Vulpiani A. The mechanism of stochastic resonance[J]. Journal of Physics A,1981, (14): L453-L457.

[6] H?nggi P.Stochastic resonance in biology[J]. Chem Phys Chem, 2002, (3): 285-290.

[7] Yasuda H, Miyaoka T, Horiguchi J, et al. Novel Class of Neural Stochastic Resonance and Error-Free Inform- ation Transfer[J]. Physical Review Letters, 2008, (100): 118103.

[8] Sun ZK, Yang XL, Xiao YZ, et al. Modulating resonance behaviors by noise recycling in bistable systems with time delay[J]. Chaos, 2014, (24): 023126.

[9] 方次軍,劉先斌.色噪聲與乘性信號驅動下昆蟲爆發系統的穩定性和隨機共振[J].江西師范大學學報,2017, (41):623-628.

[10] Shen CS, Chen HS, Zhang JQ. Amplified Signal Response by Neuronal Diversity on Complex Net- works[J]. Chinese Physics Letters, 2008, (5): 1591- 1594.

[11] Zaikin AA, García-Ojalvo J, Schimansky-Geier L, et al. Noise Induced Propagation in Monostable Media[J]. Physical Review Letters, 2002, (88): 010601.

[12] Volkov EI, Ullner E, Zaikin AA, et al. Oscillatory amplification of stochastic resonance in excitable systems[J]. Physical Review E, 2003, (68): 026214.

Stochastic Resonance Driven by Colored Noise

ZHANG Zhen, SONG Qun-qun, YANG Hui-jing

(Department of Physics, Tangshan Normal University, Tangshan 063000, China)

The dynamics of Brownian particles in a one-dimensional double potential well was studied. The simulation results show that there is stochastic resonance in a one-dimensional double potential well. The temporal coherence of the Brownian motion can reach a maximum level for an optimal colored noise intensity. The autocorrelation time of colored noise affects the synchronization behavior of the Brownian particle with a periodic signal.

Stochastic resonance; Colored noise; Q factor; Correlated time

O324

A

1009-9115(2020)03-0055-03

10.3969/j.issn.1009-9115.2020.03.013

唐山師范學院博士后基金項目（2018A03），河北省教育廳項目（QN2018308）

2019-09-09

2020-04-12

張珍（1986-），女，山東棗莊人，博士，講師，研究方向為理論計算物理化學。

（責任編輯、校對：侯 宇）