基于教材整合的復習課教學*
——以“空間垂直關系”為例

江蘇省蘇州市田家炳實驗高級中學 (215004) 李雋易

復習課是數學教學中的重要課型之一，其目的是幫助學生系統整理所學知識，形成結構化的認知，并在問題解決過程中融會貫通，實現知識的內化．教材是課程的載體，也是高考題的源頭，因此，回歸教材、整合教材是復習課教學的重要前提．立足復習課的特點，基于教材整合的復習課教學應整合知識，綱舉目張；整合例習題，尋根探源；探究變式，融會貫通．

1.整合知識，綱舉目張

整合知識的行為，來源于對運用知識的訴求．理解學科的基本結構是運用知識的最低要求，而理解知識的適用情境，則有利于問題識別與知識激活．因此，可從兩個方面進行知識整合．

一是，強調知識聯系，明晰知識結構．例如，立體幾何章節中“空間垂直關系”主要包括兩直線垂直、直線與平面垂直、平面與平面垂直三個主要內容，以及它們之間的相互關系．如圖1所示，復習時可畫出知識結構圖，以幫助學生形成結構良好的知識體系．

圖1

二是，強調問題統領，明確適用情境．有關“空間垂直關系”的證明問題主要包括異面直線垂直、線面垂直以及面面垂直問題．在復習時，可直接提出問題，“可證明兩條異面直線垂直的方法有哪些”“可證明直線與平面垂直的方法有哪些”“可證明平面與平面垂直的方法有哪些”，以幫助學生從問題解決的角度梳理數學知識．

實行多樣化的知識整合，有助于學生從不同角度去審視知識、理解知識，為知識運用做好準備．

2.整合例習題，尋根探源

教材例習題由教材編寫者精心編制，既是運用數學知識的典型案例，又是反映數學思想的重要載體．橫向來看，同一個知識點通過不同的現實模型來呈現，體現了數學表征與數學應用的多樣性，有利于學生把握數學知識的實質；縱向來看，分布在不同章節中的一系列知識點通過同一現實模型來呈現，從數學問題的層層推進中，展現數學研究的不斷深入，既有利于學生把握知識點之間的聯系，也有利于學生領會、掌握分解問題、轉化問題進而解決問題的方法．其中，教材例習題的橫向整合更適合于新授課，而縱向整合更適用于復習課．

以“空間垂直關系”為例，教材對正方體模型的研究，貫穿了異面直線垂直、直線與平面垂直、平面與平面垂直的學習過程．復習課中可通過再現、重組、改編等方式，整合相應的例習題，實現數學問題的“有層次推進”．

例1 在正方體ABCD-A1B1C1D1中．

(1)求證：BD⊥平面AA1C；

(2)求證：A1C⊥BD；

(3)求證：A1C⊥BC1；

(4)求證：A1C⊥平面BC1D．

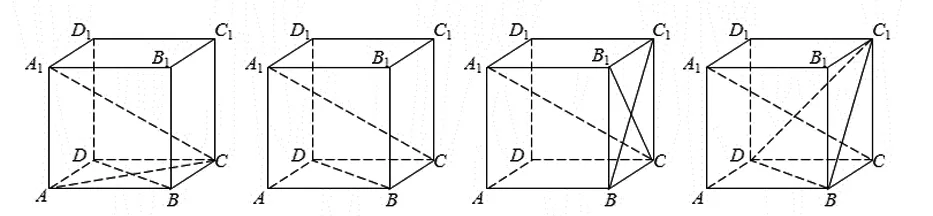
圖2 圖3 圖4 圖5

證明：(1)如圖2所示，在正方體ABCD-A1B1C1D1中，AA1⊥平面ABCD，BD?平面ABCD，所以BD⊥AA1．因為四邊形ABCD為正方形，所以BD⊥AC．又因為AA1∩AC=A，AA1?平面AA1C，AC?平面AA1C，所以BD⊥平面AA1C．

(2)如圖3所示，由(1)知，BD⊥平面AA1C，又因為A1C?平面AA1C，所以A1C⊥BD．

(3)如圖4所示，連結B1C．在正方體ABCD-A1B1C1D1中，A1B1⊥平面BCC1B1，BC1?平面BCC1B1，所以BC1⊥A1B1．因為四邊形BCC1B1為正方形，所以BC1⊥B1C．又因為A1B1∩B1C=B1，A1B1?平面A1B1C，B1C?平面A1B1C，所以BC1⊥平面A1B1C．又因為A1C?平面A1B1C，所以A1C⊥BC1．

(4)如圖5所示，由(2)(3)知，A1C⊥BD，A1C⊥BC1，又因為BD∩BC1=B，BD?平面BC1D，BC1?平面BC1D，所以A1C⊥平面BC1D．

說明：例1改編自蘇教版《必修2》第38頁練習的第3題，第41頁習題1.2(2)的第7題、第15題．其中，第(3)小問是第(1)(2)問的簡單遷移運用，而第(4)小問則是第(1)(2)(3)問的組合運用．

例2 在正方體ABCD-A1B1C1D1中，E為線段AA1中點．求證：

(1)A1C∥平面BDE；

(2)平面BDE⊥平面BC1D．

圖6

證明：(1)如圖6所示，在正方體ABCD-A1B1C1D1中，連結AC交BD于O，則O為AC中點．因為E為AA1中點，所以OE為△BDE中位線，即EO∥A1C．又因為EO?平面BDE，A1C?平面BDE，所以A1C∥平面BDE．

(2)由例1知A1C⊥BD，A1C⊥BC1．由例2(1)知EO∥A1C．所以EO⊥BD，EO⊥BC1．又因為BD∩BC1=B，BD?平面BC1D，BC1?平面BC1D，所以EO⊥平面BC1D．因為EO?平面BDE，所以平面BDE⊥平面BC1D．

說明：例2改編自蘇教版《必修2》第69頁復習題的第17題．其中，例2(2)則是例1與例2(1)的組合運用．

點評：例2(2)是一道較為復雜的問題，學生通過例1、例2的學習，體會數學問題由簡單到復雜的演變過程，領會分解問題、轉化問題的思想，學會在研究數學問題時識別數學問題“小的時候的樣子”，進而找到解決問題的切入點和突破口．與此同時，在數學運用的過程中，領會、掌握知識間的聯系．

3.探究變式，融會貫通

解決問題的變式是聯結未解決的復雜問題和已解決的簡單問題之間的一系列中介問題，其主要作用是為化歸提供鋪墊．從這個意義上來說，整合后的教材例習題，本就是一系列的變式．而在復習課教學中，可在此基礎上進一步延拓，形成新的變式，繼續推進對現實模型的研究，進一步培養學生綜合運用相關知識研究問題的能力．

另一方面，也可將整合后的教材例習題視為問題解決的樣例．將學生在師生互動下的問題探究視為對問題解決樣例的學習．因此，教學中應提供樣例的變式，以幫助學生在樣例方法的遷移過程中，深化對相關問題解決方法、策略的理解與融通．

變式在正方體ABCD-A1B1C1D1中，E為線段AA1中點，記AC∩BD=O，求證：C1O⊥平面BDE．

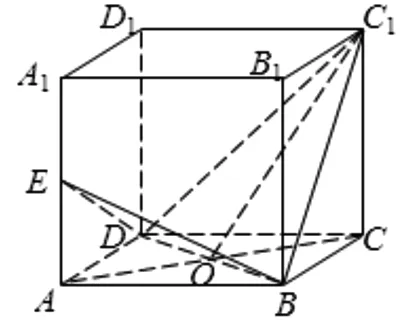
圖7

證法1:(結論推進)如圖7所示，在正方體ABCD-A1B1C1D1中，因為四邊形ABCD為正方形，AC∩BD=O，所以O為BD中點．因為C1B=C1D，所以C1O⊥BD．由例2知平面BDE⊥平面BC1D．又因為平面BDE∩平面BC1D=BD，C1O?平面BC1D，所以C1O⊥平面BDE．

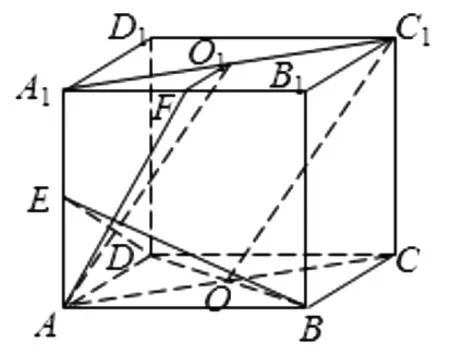
圖8

證法2:(方法遷移)如圖8所示，在正方體ABCD-A1B1C1D1中，連結A1C1，分別取A1C1,A1B1中點O1,F，連結AF,FO1,AO1．

因為AA1∥BB1且AA1=BB1，BB1∥CC1且BB1=CC1，所以AA1∥CC1且AA1=CC1，故四邊形ACC1A1為平行四邊形，所以AC∥A1C1且AC=A1C1．又因為O,O1分別為AC,A1C1中點，所以AO∥O1C1且AO=O1C1，故四邊形AOC1O1為平行四邊形，所以AO1∥OC1．

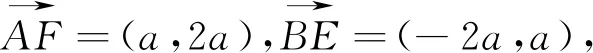
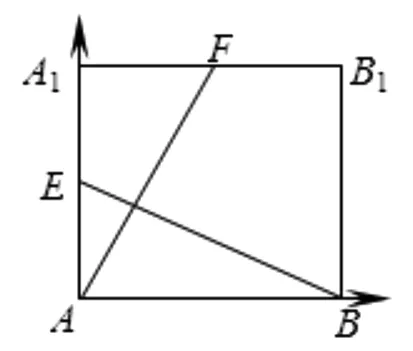
圖9

點評:該題為例1、例2的變式，與例1、例2結構相似但更為復雜，并且不同的遷移視角，反映出的證明方法也不同．證法1是對例2結論的進一步推進，學生可在例2的基礎上聯結更多的數學知識，深化對知識結構的理解．而例1、例2也為變式的解決提供了較多鋪墊，使得學生可以順利地解決較為困難的問題．證法2是對例1解題方法的遷移，學生可在此過程中鞏固所學，并解決相似解法中的新問題，進而深化對解題方法的理解．