探求圓錐曲線離心率的幾個途徑

江蘇省紹興市越州中學 (312000) 劉立鋒

我們知道，圓錐曲線的離心率是反映圓錐曲線幾何特征的一個重要數值，因此在解決圓錐曲線的離心率問題時，必須抓住圓錐曲線的定義、幾何意義和相關性質等信息，建立關于曲線的三個特征數a、b、c的等量關系，然后變形求解，請看題例分析．

一、抓住曲線定義

圓錐曲線的定義是所有圓錐曲線問題的根本，所以在關于曲線上的動點問題時，定義的運用是一個重要的思考方向．

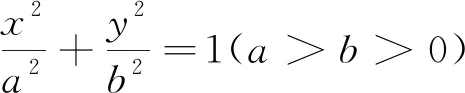
二、利用曲線方程

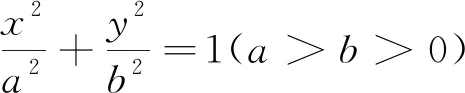
圖1

三、探求a,c的關系

從所給的條件中，直接求出a,c的值或找到a與c之間的關系式，就能解決問題了，這里需注意到對應曲線中a,b,c之間的關系．

四、挖掘幾何性質

在給出的幾何圖形中，要深挖它的幾何性質并與所求的圓錐曲線的基本元素聯系起來，利用其性質建立起等量關系，從而達到解題目的．

圖2

解析：由于ΔF2AB是等邊三角形，又A和B是以O為圓心，以|OF1|為半徑的圓與雙曲線左支的兩個交點，根據雙曲線的對稱性和等邊三角形的對稱性可知，點A、B關于x軸對稱，即線段AB垂直x軸并被x軸平分，則有∠AF2F1=30°.連AF1，由于圓O是ΔAF2F1的外接圓，則∠F1AF2=90°，又|F1F2|=2c，故有

五、進行代數運算

在具體的解題過程中，有的時候會遇到復雜的運算與推理，我們要細心加耐心，加恒心，堅持運算，直到完成解題目標．

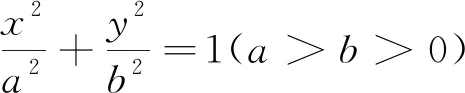
圖3