例談絕對值不等式與柯西不等式的綜合運用*

河南大學數(shù)學與統(tǒng)計學院 (475004) 胡昊宇

由于在各類試題中關(guān)于絕對值不等式與柯西不等式的綜合運用較為常見，所以我們應(yīng)引起足夠的重視.為了強化這一方面的運用能力，請結(jié)合以下歸類解析認真領(lǐng)會，以便逐步提高處理此類問題的求解能力.

類型一 給定絕對值不等式的解集，利用柯西不等式求最值

首先，需要根據(jù)絕對值不等式的解集，準確求解其中參數(shù)的取值；然后根據(jù)表達式的外在結(jié)構(gòu)特點，即可靈活運用柯西不等式巧求最值.

例1 已知關(guān)于x的不等式|x+4|+|x-m|≤5的解集為{x|-4≤x≤1}．

(Ⅰ)求實數(shù)m的值；

(Ⅱ)若a2+2b2+3c2=m，求a+4b+9c的最值．

分析：(Ⅰ)需要先根據(jù)所給解集，通過考查特殊情形得到實數(shù)m的值，然后再加以檢驗分析.(Ⅱ)需要先根據(jù)(Ⅰ)的結(jié)論明確已知條件，再靈活利用柯西不等式求目標式的最值.

解析：(Ⅰ)依題意，當x=1時不等式成立，所以5+|1-m|≤5，解得m=1.經(jīng)檢驗知m=1適合題意.故所求實數(shù)m的值為1.

(Ⅱ)由(Ⅰ)知a2+2b2+3c2=1，所以根據(jù)柯西不等式得(a+4b+9c)2≤(1+8+27)(a2+2b2+3c2)=36×1=36，即-6≤a+4b+9c≤6.

評注：理清絕對值不等式的解法，明確不等式的解集與對應(yīng)方程的根之間的關(guān)系，掌握利用柯西不等式求最值的技巧，是順利分析、求解此類問題的關(guān)鍵所在.

類型二 利用柯西不等式求最值，考查絕對值不等式中的恒成立問題

靈活運用柯西不等式，可求解含有多個變量的代數(shù)式的最值；處理有關(guān)含參數(shù)的絕對值不等式恒成立問題時，往往需要關(guān)注絕對值三角不等式在解題中的靈活運用.

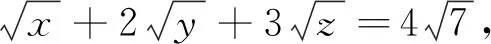
(Ⅰ)求k的值；

(Ⅱ)若a≤|x+6|+|k-x|對任意x∈R恒成立，求實數(shù)a的取值范圍.

分析：(Ⅰ)需要靈活利用柯西不等式求x+y+z的最小值.(Ⅱ)關(guān)鍵在于靈活利用絕對值三角不等式求|x+6|+|k-x|的最小值.

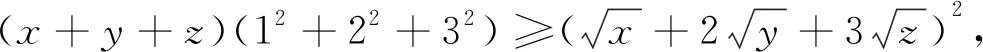
(Ⅱ)由(Ⅰ)知a≤|x+6|+|8-x|對任意x∈R恒成立，所以a≤(|x+6|+|8-x|)min.又由絕對值三角不等式得|x+6|+|8-x|≥|(x+6)+(8-x)|=14，當且僅當(x+6)(8-x)≥0，即-6≤x≤8時不等式取“等號”，所以(|x+6|+|x-8|)min=14.于是，可得a≤14.故所求實數(shù)a的取值范圍是(-,14].

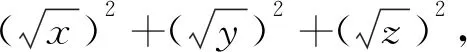
類型三 利用柯西不等式求最值，考查絕對值不等式中的是否存在型問題

靈活運用柯西不等式，可求解含有兩個根式的代數(shù)式的最值；處理是否存在型絕對值不等式問題時，往往需要借助絕對值三角不等式靈活分析、解決目標問題.

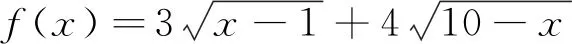
(Ⅰ)求函數(shù)f(x)的定義域和M的值；

(Ⅱ)是否存在實數(shù)x的值，使得|x-10|+|x+5|≤M？若存在，求出滿足條件的實數(shù)x的取值范圍；若不存在，請說明理由.

分析：(Ⅰ)求函數(shù)的定義域比較簡單，難點在于靈活利用柯西不等式求函數(shù)f(x)的最大值.(Ⅱ)求解關(guān)鍵在于先利用絕對值三角不等式分析|x-10|+|x+5|的取值范圍，再靈活轉(zhuǎn)化目標問題.

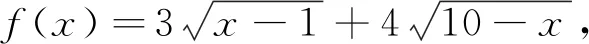
(Ⅱ)由(Ⅰ)知：本小題即考查是否存在實數(shù)x的值使得|x-10|+|x+5|≤15．因為由絕對值三角不等式得|x-10|+|x+5|≥|(x-10)-(x+5)|=15，所以滿足不等式|x-10|+|x+5|≤15的解x就是方程|x-10|+|x+5|=15的解.又由絕對值的幾何意義可知：當且僅當-5≤x≤10時，|x-10|+|x+5|=15.故存在實數(shù)x∈[-5,10]，使得|x-10|+|x+5|≤M.

評注：(1)結(jié)合本題，我們應(yīng)關(guān)注兩點：一是柯西不等式的外在結(jié)構(gòu)以及運用的靈活性(正用、逆用、變形用)；二是絕對值三角不等式在解題中靈活運用.

類型四 給定絕對值不等式的解集，利用柯西不等式的取等條件巧求值

首先，需要由解集求參數(shù)的取值；然后根據(jù)表達式的外在結(jié)構(gòu)特點，不但要考慮柯西不等式的活用，而且還要考慮柯西不等式的取等條件，以便根據(jù)題設(shè)條件巧求有關(guān)代數(shù)式的值.

例4 已知函數(shù)f(x)=|x+7|，g(x)=m-|x-3|(m∈R)，且不等式f(x)-g(x)≤0的解集為{x|-9≤x≤5}.

(Ⅰ)求實數(shù)m的值；

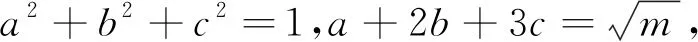
分析：(Ⅰ)需要先明確不等式，再通過構(gòu)造函數(shù)，利用函數(shù)的圖像及所給不等式的解集加以靈活分析.(Ⅱ)關(guān)鍵在于靈活利用柯西不等式的“取等”條件，巧妙求解目標式的值.

解析：(Ⅰ)由題設(shè)知，不等式f(x)-g(x)≤0，即為|x+7|+|x-3|≤m.設(shè)函數(shù)F(x)=|x+7|+|x-3|，則結(jié)合函數(shù)F(x)的圖像及所給不等式的解集可知，所求m=F(-9)=F(5)=14.

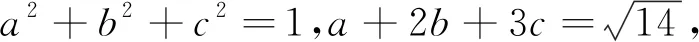
評注：結(jié)合本題，我們應(yīng)關(guān)注兩點：一是要理清絕對值函數(shù)的圖像特征；二是要理清柯西不等式的“取等”條件.

綜上，關(guān)注絕對值不等式與柯西不等式的綜合運用，有利于加深對絕對值不等式和柯西不等式本身的理解與認識，有利于提高綜合運用能力，拓展解題思維，提升解題技能！