數形結合思想方法應用舉例
——觀數思形妙轉化

陜西省漢中市四〇五學校 (723312) 侯有岐

一、考點回顧

在近幾年的高考試題中，觀數思形，利用數形結合思想解題是高考數學中解決部分函數選填壓軸題時常用的解題技巧之一，這也是數形結合思想的最基本應用.對于某些函數最值問題，有時候通過求導數、判斷函數單調性的處理策略無力解決時，我們不妨觀數思形，從圖像的角度來思考分析，可以通過觀察函數圖像，給待求式賦予一定的幾何意義，從而尋求問題的解決.本文通過實例，展示觀數思形、巧妙轉化及利用數形結合轉化思想解決函數相關問題的常用方法.

二、典例剖析

例1 (陜西省漢中市四〇五學校2018年高三模考題理12)已知關于x的函數y=(x-a)2+(ex-a+1)2(a∈R)的最小值為m(a)，求m(a)的最小值.

分析：此題并非常規函數類型，初步想法是可以通過求導數，然后判斷函數的單調性，以此求出函數的最小值y′=2x-2a+2e2x-2(1-a)ex，在求解y′=0時遇到非常大的困難，這樣單調性就無法判斷.那么，換個角度思考，觀察函數的表達式，可以發現函數表達式是由兩個完全平方式構成，自然聯想到平面上兩點之間的距離公式，于是可以將問題轉化成求兩點P(x,ex),Q(a,a-1)之間的最短距離的平方來處理.

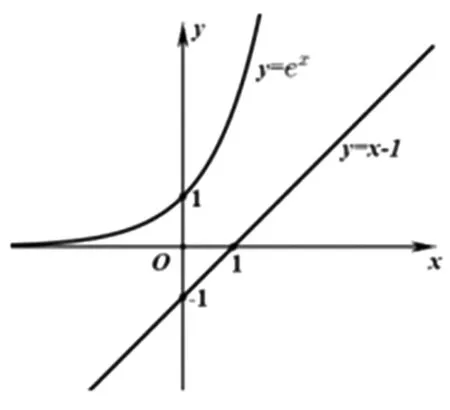
圖1

解法一：設P(x,ex),Q(a,a-1)，則y=PQ2，且點P(x,ex)為函數y=ex圖像上的一個動點，點Q(a,a-1)為直線y=x-1上一動點，如圖1所示.

將直線y=x-1向y=ex方向平移，與其相切，設切點為P，過P作直線y=x-1的垂線段，垂足為Q，此時的PQ為最小值.

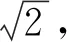
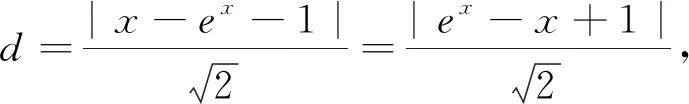
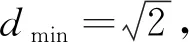
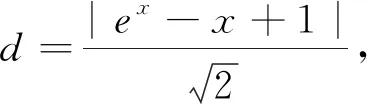
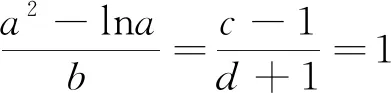
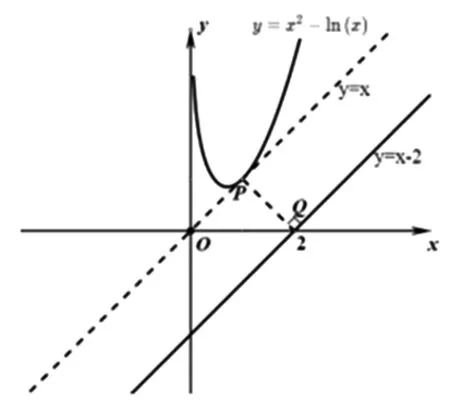
圖2

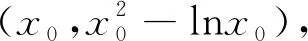
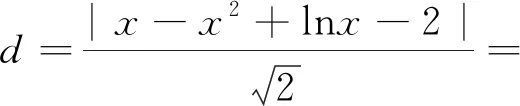
例3 (漢中市四〇五學校2018年高三模考題)在坐標平面內,與點A(1,2)的距離為1,且與點B(3,1)的距離為2的直線共有( )條.

(A)1 (B)2 (C)3 (D)4

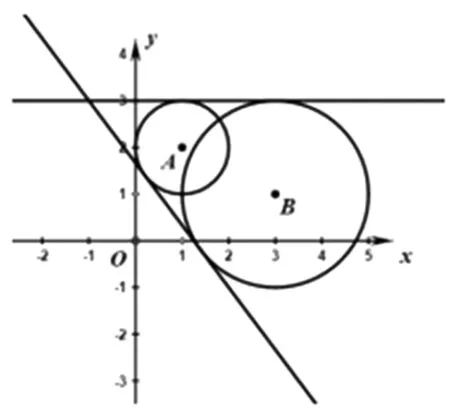
圖3

分析：將數的問題輔以形的意義,利用圓的定義畫出分別以A(1,2)、B(3,1)為圓心，以1、2為半徑的兩個圓,然后再根據兩圓的位置關系,把問題轉化為研究兩圓的公切線的條數.

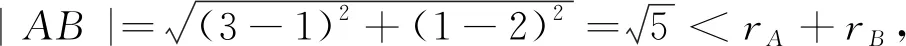
評注：本題若直接求解比較困難，但若觀數思形，將數的問題輔以形的意義，就有事半功倍的效果，其實這樣的方法在高考題中屢見不鮮，要引起高度重視.

例4 (漢中市四〇五學校2018年高三模考題)豎立在地面上的兩根旗桿的高分別為10米和15米，相距20米，則地面上到兩根旗桿頂點的仰角相等的點P的軌跡是( ).

(A)圓 (B)橢圓 (C)雙曲線 (D)拋物線

分析：由于P點在地面上,因而只要將動點P所受的空間限制條件轉化為動點P在地面上的限制條件,再由相關知識即可求出.

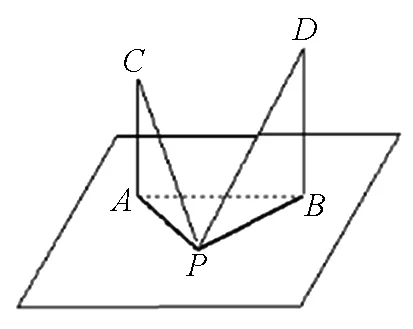
圖4

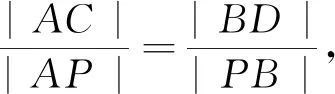
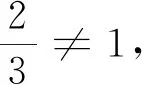
三、總結反思

數形結合的思想是我們平時做題時最常用的方法之一，數的抽象可以通過形的直觀來理解，數形結合就是實現代數與幾何之間的相互轉化，具體應用表現在以下兩個方面：

1.通過坐標系、圖像等，“形”題“數”解

借助直角坐標系可以將圖形問題代數化，這一方法在解析幾何和立體幾何中體現的相當充分,常與以下內容聯系：①實數與數軸上點的對應關系；②函數與圖像的對應關系；③曲線與方程的對應關系；④以幾何元素和幾何條件為背景，建立起來的概念，如向量、三角函數等.⑤以函數圖像為載體，解決有關函數最值等問題.

2.通過轉化構造，“數”題“形”解

在解題過程中，許多代數結構有著明顯的幾何意義，因此，可以將“數”與“形”進行巧妙地轉化靈活解題.如本文所舉的例題.另外，函數的圖像也是實現數形結合的有效工具之一.因此，函數思想和數形結合思想經常結合起來應用于解題.

四、高考預測

從目前高考“注重通法，淡化特技，培養素養”的命題原則來看，高考對數形結合的考查主要體現在以下三個方面：一是利用數形結合直觀、簡捷地解答選擇題、填空題；二是利用數形結合求解解答題，特別是向量法、坐標法在立體幾何、解析幾何中的應用及函數圖像在函數與導數綜合問題中的應用；三是以圖表為載體，考查讀圖、識圖及信息轉換能力.這種問題在選擇、填空題中有增加題量的趨勢.

總之，數形結合思想其實質是將抽象的數學語言與直觀的圖像結合起來，關鍵是代數問題與圖像之間的相互轉化，它可以是代數問題幾何化，幾何問題代數化.