粘結式錨桿錨固機理數值模擬研究
張守文
廣州市城市規劃勘測設計研究院,廣東 廣州 510060
1 引言
錨固系統主要由錨桿、注漿材料、巖體及粘結劑等組成。除桿體力學特性較簡單外,注漿材料和巖體等材料均具有復雜的力學特性,各介質之間相互作用及荷載傳遞機理、應力分布及演化規律非常復雜。
國內外學者開展了許多研究工作。黃明華[1]等通過建立非線性剪切滑移模型,獲得錨固段軸力和剪應力解析解,發現剪應力峰值點。Farmer[2]以彈性假設推導出一維情況下剪應力沿著錨固段呈負指數分布。黃生根[3]等通過建立顆粒流數值模型,分析了錨固系統細觀力學特性。張季如[4]等,通過假定界面剪應力與位移呈線性關系,建立了荷載雙曲線模型。葉根飛[5]等通過實驗,研究了應力沿界面長度分布規律。但是考慮巖土體剪脹效應及粘結劑與巖體界面作用的研究還較少。本文通過設置界面層單元,利用ANSYS 建立有限元模型,探討粘結式錨固系統荷載傳遞機理。
2 粘錨力計算
假設桿體與鉆孔間的間隙為定值,則剪應力同桿體與孔壁間相對位移成正比,則x 點處的粘結力[5]:
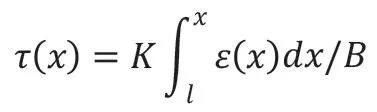
式中:ε(x)為x 點處拉應變;K 為剛度系數;B 為間隙寬;l 為錨固長度。軸力:
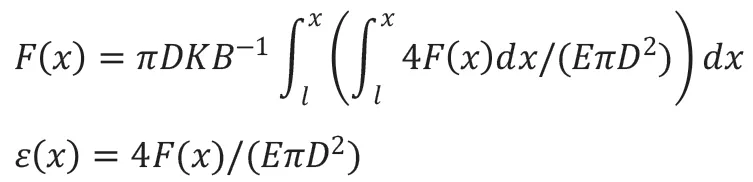
3 數值分析
3.1 幾何模型
建立軸對稱模型,如圖1 所示。圍巖外施加x 方向約束,底部施加y 方向約束。巖體、灌漿體采用彈塑性模型,錨桿采用線性彈性模型。巖體、注漿體和界面層采用實體單元plane42單元。桿體直徑20mm,錨固長度1000mm,灌漿體直徑40mm,界面層厚度2mm,深度1500mm,模型圍巖直徑1000mm。
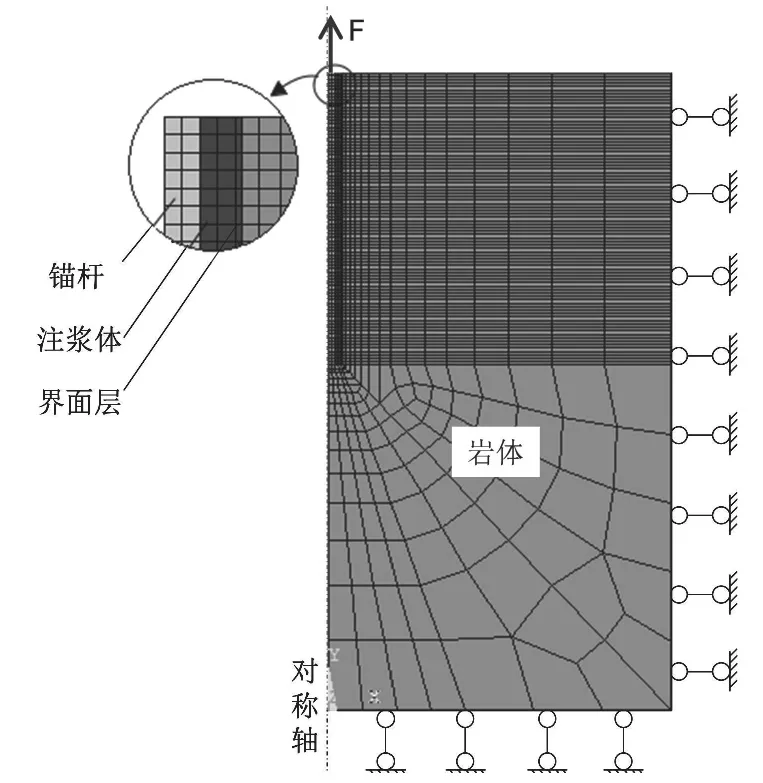
圖1 劃分網格后的有限元模型
3.2 定義屬性
巖體與粘結劑選擇Drucker-Prager本構模型。錨桿材料為線彈性材料,采用Mises 模型。屈服準則D-P:
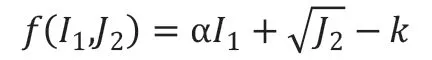
式中:I1,J2分別為力張量的第一、第二不變量;α、k 是與材料性質有關的參數。錨桿、界面層、注漿體、巖體的材料屬性如表1 所示。

表1 材料屬性表
4 計算及分析
(1)施加25KN、50KN、140KN 的載荷,結果如圖2 所示。剪應力呈現非線性分布,沿錨固方向先增加,后逐漸減小,達到峰值后成負指數遞減。軸向應力隨載荷的增加而增大,也呈現負指數遞減的規律。

圖2 剪應力與軸應力演化曲線
(2)建立錨固長度分別為0.5m、0.8m 和1m 的模型,施加10KN、35KN和50KN集中載荷,結果如圖3所示。當長度為0.5m時,有效錨固長度占總長度比重較大,錨桿得到有效利用。長度為0.8m 和1.0m 時,隨著荷載的增加,剪應力分布逐漸向深部擴展。只是荷載向深部傳遞的速度不是很快。并沒有明顯增加有效的錨固長度。因此,當錨固長度較小時,適當增加錨固長度能夠增大錨固力;當錨固長度比較大時,單純的增加錨固長度對提高錨固力貢獻不大。
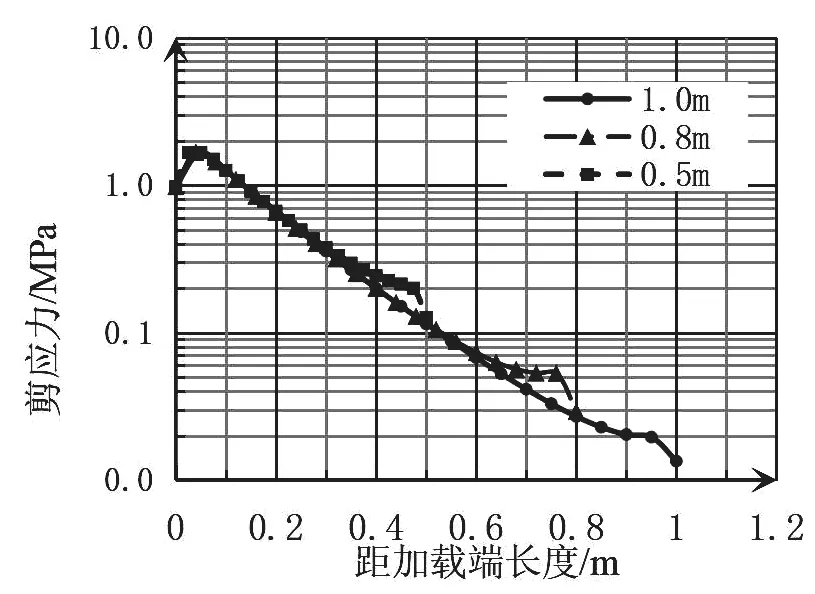
圖3 不同錨固長度下剪應力圖(50KN)
5 結論
拉拔狀態下錨固體界面剪應力呈現非線性分布,先增加后呈負指數遞減。荷載越大,峰值剪應力越大,擴散的距離越遠。軸向應力也近似呈現負指數遞減的規律。
錨固長度相對比較短時,有效錨固長度占整個錨固長度比重較大,此時,適當增加錨固長度能夠增大錨固力;但當錨固長度比較大時,可以通過提高前端粘結性能提高錨固能力。

