一類三次微分系統的時間可逆與中心問題
楊 靜,楊 鳴,陸征一
(1.中國科學院成都計算機應用研究所,四川成都610041; 2.中國科學院大學,北京100049;3.四川師范大學數學科學學院,四川成都610066)
1 預備知識
時間可逆是自然科學中最重要的對稱性原理之一,其概念源于Birkhoff對三體運動的研究[1].文獻[1]的模型存在對合映射,且此模型是關于這個對合映射的不動點集合對稱的.周期解一直是微分動力系統關注的對象.特別是1900年Hilbert提出了著名的23個問題后,極限環和中心成為學者們不斷關注的焦點.1976年,Devaney[2]給出了可逆系統的定義.特別地,對平面解析微分系統,可逆中心也是一個廣泛研究的課題.關于可逆微分動力學的研究見文獻[2-3].2000 年,Zhang 等[4]得到了一類特殊三次可逆系統弱中心的條件.2001年,Teixeira等[5]得到:如果系統的一次近似為(-y,x),那么系統是φ-時間可逆的當且僅當原點是它的中心,并獲得當系統一次近似為(y,0)時,原點是中心的充分或必要條件.2008年,Romanovski[6]給出了尋找給定二維多項式自治微分系統是時間可逆系統的 Zariski閉集的算法.2011 年,Giné等[7]研究了退化和非退化情形下的時間可逆和中心的關系.2017年,Wei等[8]研究了廣義對合微分可逆系統的性質.2018年,Han等[9]研究了平面多項式微分系統可以通過仿射變換變成時間可逆系統的條件.
對于給定的多項式微分系統

判斷原點是否為該系統的中心型平衡點,一般地,用Poincaré形式冪級數法.但實際上該方法依賴于焦點量的計算,這對計算機代數系統來說是十分復雜的任務.因此,通常將得到中心充要條件的過程分為兩步:首先通過計算系統的前幾階焦點量得到中心的必要條件,然后再判斷這些必要條件是否充分.充分性的驗證,可以通過積分因子[10]和Poincaré原理[11]來做到.實際上,時間可逆是Poincaré對稱原理的一般化.這是因為,滿足Poincaré對稱原理的系統也是在特殊映射下的時間可逆系統,只需要映射使得系統的相圖關于坐標軸對稱.后面將在第二節對其進行詳細討論.即便如此,計算焦點量仍舊十分困難,特別是在階數高的情形.理論上可以利用時間可逆系統和中心的關系,得到標準型中心焦點系統為中心的充要條件,從而避免復雜的焦點量計算.
Wang[12]考慮了一類三次系統

并給出了該系統原點為中心的充分條件.最近,唐璐等[13]利用時間可逆系統的性質得到了系統(2)的另一組原點為中心的充分條件.本文利用時間可逆系統性質,得到了其在線性對合下時間可逆的充要條件.再利用時間可逆與中心的關系,更大程度地擴展了系統原點為中心的充分條件.解決上述問題的關鍵在于確定多項式系統的零點.計算機代數系統中的結式、Gr?bner 基方法[14]和 Regular Chain方法[15]常被用于解決這類問題.本文通過Regular Chain方法來求解多項式系統,從而得到上述多項式系統零點集的一個劃分,并通過討論這些劃分中的含參系統有實數解的充要條件,得到系統是時間可逆的充要條件.
2 Poincaré對稱原理與時間可逆系統
考慮 Cr微分系統(r∈N∪{∞,ω}),

F(x)∈R2是一個向量值函數,且原點是其對應線性系統的中心.N是正整數集合,C∞表示無窮光滑代數,Cω表示在規定區域內定義的解析函數.
定義1[5]系統(3)是時間可逆的,如果存在一個微分同胚映射φ滿足φ?φ=Id,使得

其中,XF是與系統(3)對應的向量場,Id表示恒等映射,?表示2個映射的合成,φ*表示φ的切映射,即在局部坐標系上 φ*XF=Dxφ(x)F(x),其中Dxφ(x)是 φ 關于 x的雅可比矩陣.滿足 φ ?φ=Id的映射φ被稱為對合.
引理1[11]令系統(3)的向量場

若其關于x1軸或x2軸對稱,即
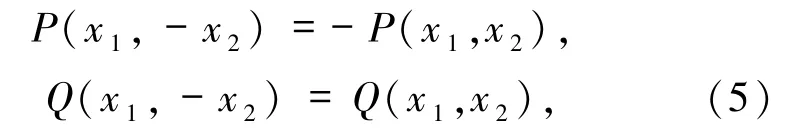
或

則原點必為中心.
稱引理1為Poincaré原理,它給出了系統(3)為中心的充分條件,即向量場是關于x1軸或x2軸對稱的.可以注意到系統(3)在滿足向量場是關于x1軸或 x2軸對稱的條件(5)或(6)時,也是關于映射

或
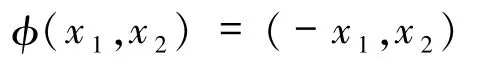
時間可逆的.一般地,有如下直接的結果.
引理2若系統(3)在映射φ下是時間可逆的,則原點是系統(3)的中心,其中
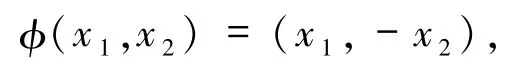
或

考慮二維多項式微分系統

其中

f(x)=o(|x|)是一個 2 維多項式函數,而(R2,0)表示原點的鄰域.我們有引理3.
引理3[5]系統(7)是時間可逆的當且僅當原點是中心.
3 線性對合時間可逆的充要條件
下面給出系統(7)在線性映射下是時間可逆的充要條件.令
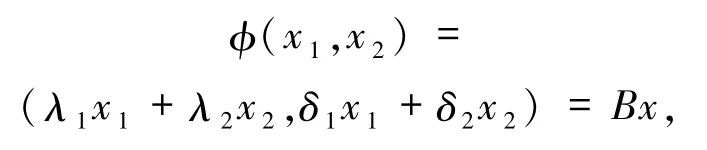
其中 λ1,λ2,δ1,δ2∈R,而

由定義1可知系統(7)在φ下時間可逆,需要滿足以下條件:
1)φ是一個對合,即滿足條件(不考慮B=±E這種平凡的情況)

2)(4)式成立,即

其中包含條件 φ(Ax)=-(Aφ(x)),因為

所以有λ2=δ1且-λ1=δ2.
自然地,有如下直接的結果.
引理4系統(7)在映射 φ(x1,x2)=(λ1x1+λ2x2,δ1x1+δ2x2)下時間可逆當且僅當

其中 x=(x1,x2).
由引理4,不妨假設線性對合φ為

令

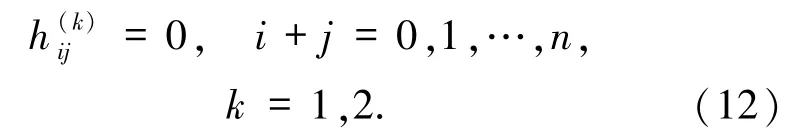
令

由引理4,系統(7)在線性對合下時間可逆的充要條件即為多項式方程組Cof關于變量λ1和λ2有實數解的充要條件.
考慮三次多項式微分系統(2)線性對合時間可逆的問題,得到了系統在線性對合下是時間可逆的充要條件.
定理1系統(2)在線性對合下是時間可逆的,當且僅當下列條件之一成立:


再由引理3,得到此條件也是原點為系統(2)的中心的充分條件.
4 定理1的證明
首先,由引理4提取出與系統(2)對應的多項式方程組Cof,含有15個方程,特別地,

使用計算機代數系統Maple上的實三角化命令RegularChain:-RealTriangularize得到了方程組Cof解集的10個正則半代數集 T1,T2,…,T10(變量序為A>B>C>E>F>a>b>d>λ1>λ2).定理1中除條件3)、4)和10)以外的條件都可以直接由正則半代數集 Ti(i=2,3,…,10)得到.而條件 3)、4)和10)則可通過討論正則半代數集T1關于λ1和λ2有實解的充要條件得到的,其中,正則半代數集T1為

當 A≠B 時,由(13)和(14)式得到

將其代入(16)式,經過變換可以得到 d(25(AB)2+d2)ω =0.因為 λ2≠0,所以 d≠0,則需 ω =0.由不等條件可以得到d2-75(AB)2≠0.由 A-B≠0,d≠0即可滿足 -1<λ2<1.從而得到定理1中條件10).
當A=B時,由(14)式可得dλ1=0.因為 λ1=0與(13)式使得 λ2=±1,與不等式(17)矛盾,所以d=0.又因為(15)式成立,所以C=E=F=0.將A=B,C=E=F=d=0代入T1得到
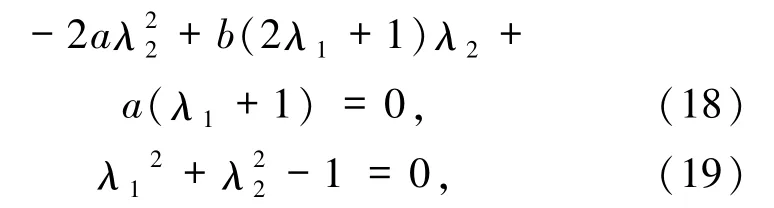
當 a=0 時,(19)式化簡為 bλ2(2λ1+1)=0,其中λ2≠0,而與(19)式使得,與不等式(17)矛盾,所以b=0.這就得到定理1中條件 3).
當a≠0時,將(18)與(19)式關于變量 λ2作結式得到

因為 λ2≠0且(19)式成立,所以 λ1≠ -1.所以(20)式等于零,需要
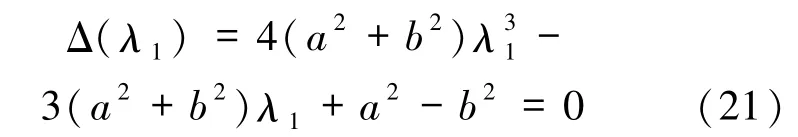
有關于變量λ1的實解,且滿足不等條件(17).當a≠0且b=0時,(21)式可以化為

此時λ2的取值與不等式(17)矛盾;而當a≠0且b≠0時,因為Δ(-1)=-2b2<0且 Δ(1)=2a2>0,所以方程(21)有滿足 -1<λ1<1的實解.又由于該解也是方程(18)和(19)的公共解,同時也需要由它解出的λ2滿足不等式(17).所以還要求Δ(0)=a2-b2≠0,即 a≠ ±b.而要求的 Δ(1/2)=-2b2≠0,Δ(-1/2)=2a2≠0 也是滿足的.這就得到了定理1的條件4).
5 討論
Wang[12]考慮了系統(2),并借助于計算機推導和Poincaré原理給出了此系統在線性對合下時間可逆中心的一組充分條件.唐璐等[13]借助于時間可逆系統性質得到了系統(2)在線性對合下時間可逆中心的另一組充分條件.本文利用時間可逆系統性質得到了系統(2)在線性對合下時間可逆中心的充要條件.定理1中的條件1)、2)和7)~10)是不同于 Wang[12]的新的充分條件.而唐璐等[13]所得三組充分條件均屬于定理1的第10)組條件.
同時,在限制A≠B,d≠0 和d2-75(A-B)2≠0的情形下回答了Wang[12]提出的一個公開問題:
猜想當如下條件成立時:
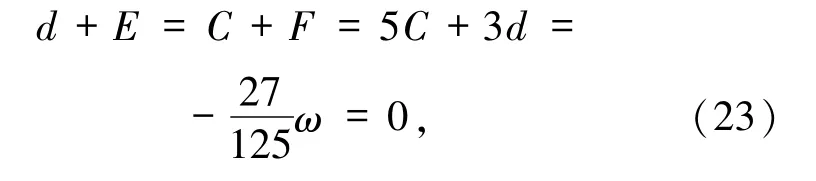
原點是系統(2)的中心.
而當限制條件不滿足時,此猜想還沒有結果.而文獻[12,16]通過不變曲線方法,利用首次積分理論判斷原點為中心,是另一種典型的中心存在性論證方式,可望在非線性對合時間可逆的中心判斷方面有所作用.

