一類在磁場(chǎng)中具有調(diào)和勢(shì)的非線性Schr?dinger方程解整體存在和爆破的門檻條件

周 凡，黃 娟*，李玉林

（1.四川師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，四川成都610066； 2.四川師范大學(xué)可視化計(jì)算與虛擬現(xiàn)實(shí)四川省重點(diǎn)實(shí)驗(yàn)室，四川成都610066）

1 引言及主要結(jié)果

帶磁場(chǎng)的非線性Schr?dinger方程是量子力學(xué)中描述在非相對(duì)論情形下粒子運(yùn)動(dòng)狀態(tài)的方程.因此，對(duì)于帶磁場(chǎng)的非線性Schr?dinger方程解的存在性以及解的相關(guān)性質(zhì)的研究受到許多人的關(guān)注.本文考慮如下帶磁場(chǎng)的非線性Schr?dinger方程：

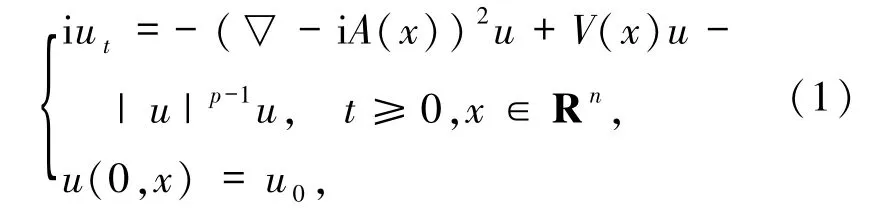
對(duì)于方程（1），當(dāng) A（x）≠0 且 V（x）=0時(shí)，Cazenave 等[1]證明了方程（1）的局部適定性和駐波的穩(wěn)定性.Cingolani[2]研究了方程（1）的多解的存在性.Tintarev[3]在一般非緊黎曼流形上證明了與哈密頓量有關(guān)的方程（1）的基態(tài)解的存在性.Bonheure等[4]研究了方程（1）的半經(jīng)典柱對(duì)稱解的存在性.Gan等[5]研究了方程（1）在負(fù)能量的情況下方程解的爆破條件.Gan等[6]研究在二維磁場(chǎng)中的非線性Schr?dinger方程，給出了解整體存在和爆破的門檻條件.Ginibre等[7]研究了方程（1）在與時(shí)間相關(guān)勢(shì)函數(shù)下的散射理論.當(dāng)n=2時(shí)，舒級(jí)等[8]通過(guò)能量法給出了方程（1）的解在有限時(shí)間內(nèi)爆破的條件.Ribeiro[9-10]研究初始能量為負(fù)時(shí)，方程（1）解在有限時(shí)間內(nèi)爆破的條件，以及初始能量為正時(shí)整體解存在的條件.

當(dāng) A（x）≠0，V（x）≠0 時(shí)，文獻(xiàn)[11-14]通過(guò)壓縮映象原理證明了當(dāng)時(shí)方程（1）的局部適定性.Liu等[15]在電勢(shì)和磁場(chǎng)勢(shì)的一些衰減和弱對(duì)稱條件下，證明了該方程具有無(wú)限多的非徑向復(fù)值解.Garcia[16]研究了方程（1）在為任意調(diào)和勢(shì)，V（x）為關(guān)于 xr的一階導(dǎo)數(shù)），div A（x）=0，▽A（x）=0 的條件下，且初始能量為負(fù)時(shí)其解在有限時(shí)間內(nèi)爆破.Cingolani[17]證明了方程（1）的爆破準(zhǔn)則.

關(guān)于方程（1），本文研究三維空間中（n=3），勢(shì)函數(shù) V（x）=｜x｜2且

磁場(chǎng)旋轉(zhuǎn)軸 Ω =（ω1，ω2，ω3）（ωi∈R）的情況.考慮初始能量為正且滿足一定條件時(shí)方程解的整體存在和爆破的門檻條件.具體地，利用方程（1）的哈密爾頓結(jié)構(gòu)建立方程（1）的發(fā)展不變流形，研究方程（1）所對(duì)應(yīng)初值問(wèn)題的爆破解和整體解存在的門檻條件.首先定義如下空間：

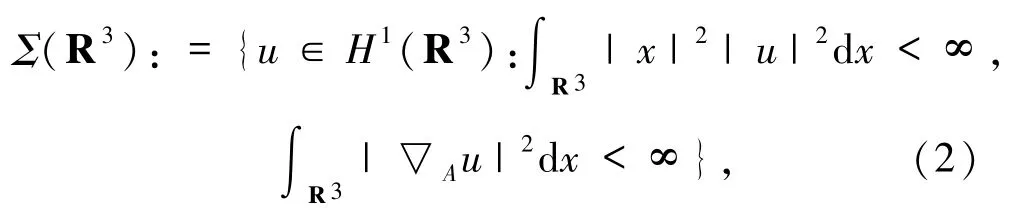
其中

當(dāng) V（x）=｜x｜2時(shí)，方程（1）對(duì)應(yīng)的質(zhì)量泛函為

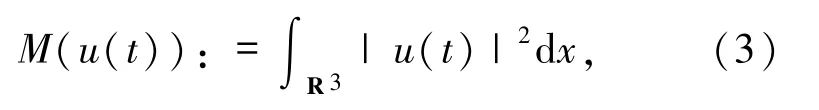
能量泛函為

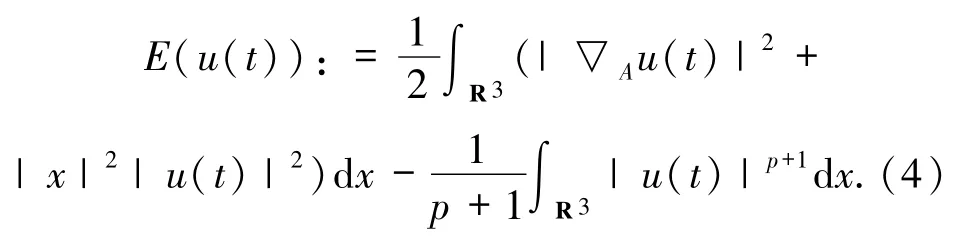
定理1.1若，V（x）=｜x｜2且，初值 u0∈Σ（R3）滿足 E（u0）＜B，則：

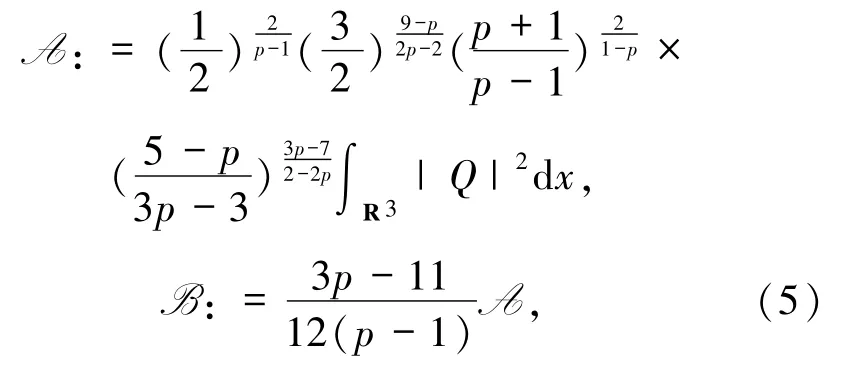
其中Q是橢圓方程-△Q+Q-｜Q｜p-1Q=0，Q∈H1（R3）的基態(tài)解.

注1.1整體解存在的條件可以擴(kuò)大到1＜p＜5，若初值 u0滿足則方程（1）的解 u（t，x）在Σ（R3）中整體存在.

2 預(yù)備知識(shí)

本文中，在不引起混淆的情況下把積分∫R3·dx 寫(xiě)成∫·dx，A（x）寫(xiě)成 A.

命題2.1（局部適定性[4，11-14]） 設(shè) 1 ＜ p ＜5，V（x）=｜x｜2，u0∈Σ（R3），那么方程（1）的唯一解u（t，x）∈C（[0，T]×Σ（R3）），其中 T∈R+是解的最大存在時(shí)間.若T=∞，則稱方程（1）的解整體存在；若T＜∞，則方程（1）的解在有限時(shí)間內(nèi)爆破.此外，當(dāng) t∈[0，T）時(shí)，u（t，x）滿足 2 個(gè)守恒率：質(zhì)量守恒

和能量守恒

引理2.1（Heisenberg 不等式[18]）

引理2.2（Gagliardo-Nirenberg 不等式[18]）設(shè)1＜p＜5并且Q是非線性橢圓方程的徑向?qū)ΨQ解

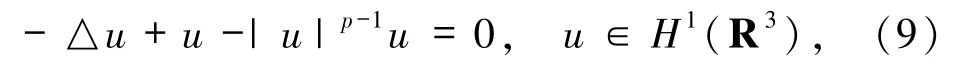
則有如下Gagliardo-Nirenberg不等式

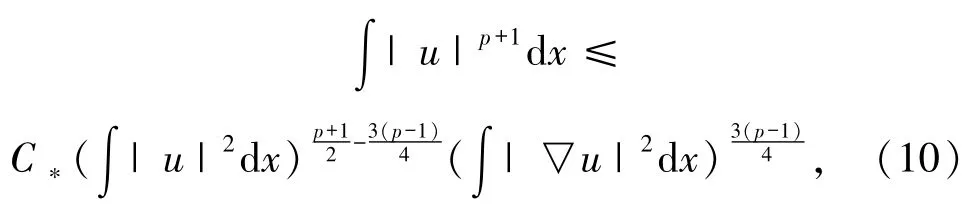
其中

命題2.2[9，16]設(shè) u0∈Σ（R3），且 u（t，x）是t∈[0，T）時(shí)方程（1）對(duì)應(yīng)于初值 u0的解，令，且

3 不變流形

設(shè)1＜p＜5，定義如下集合：

命題3.1設(shè)1＜p＜5，則 Kg和 Kb是方程（1）的不變流形，即如果初始值u0∈Kg（或Kb），則方程（1）的解 u（t，x）仍然滿足 u（t，x）∈Kg（或 Kb）.

證明設(shè) u0∈Kg，且 u（t，x）是方程（1）關(guān)于初值 u0的解.由命題3.1 知 E（u（t））=E（u0），t∈[0，T），因此，通過(guò) E（u0）＜B，可得

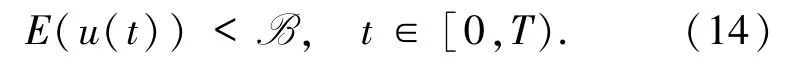
要證 u（t）∈Kg，只需證明

反設(shè)（15）式不成立，因?yàn)?/p>

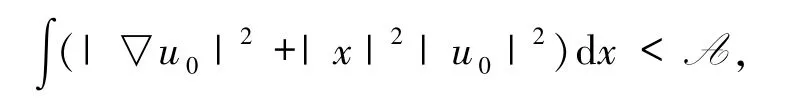
由連續(xù)性可知存在一個(gè)t1∈[0，T）使得

現(xiàn)在考慮一個(gè)實(shí)值函數(shù)

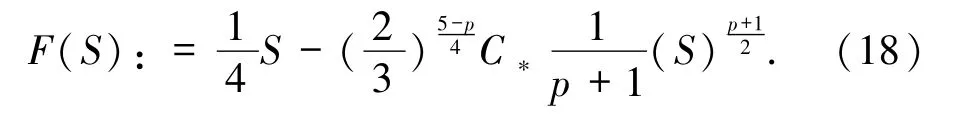
F（S）在 S∈R+上滿足：

1）當(dāng) S=A 時(shí)，F(xiàn)′（S）=0；

2）當(dāng) S=A 時(shí)，F(xiàn)″（S）＜0.

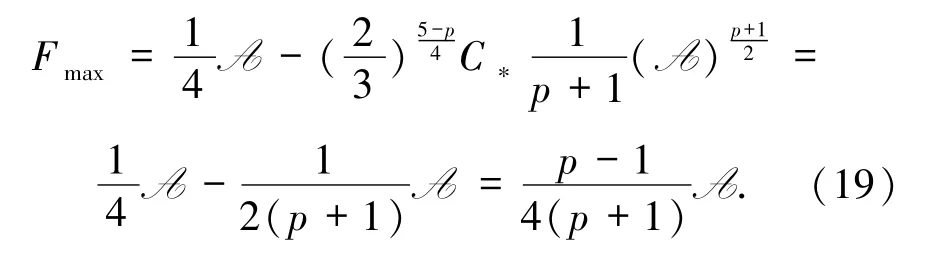
因此，通過(guò)（17）和（19）式可知

這與 E（u（t1））=E（u0）＜B 矛盾.因此，（15）式成立.

用類似方法可證Kb也是方程（1）的不變流形.

4 主要結(jié)論的證明

定理1.1的證明1）設(shè)u0∈Kg，即

當(dāng) t∈[0，T）時(shí)，由命題3.1 知，方程（1）關(guān)于初值u0的解 u（t，x）∈Kg.從而

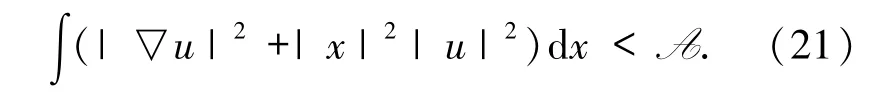
同時(shí)，由

可知結(jié)論成立.

2）設(shè) u0∈Kb，即

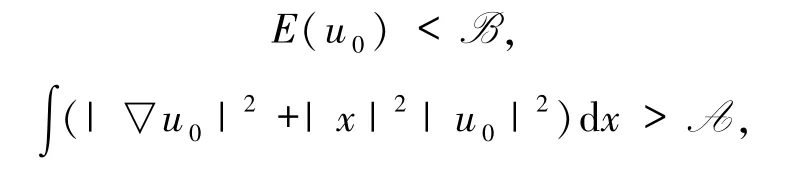
由命題3.1知方程（1）關(guān)于初值 u0的解 u（t，x）∈Kb，即

并且

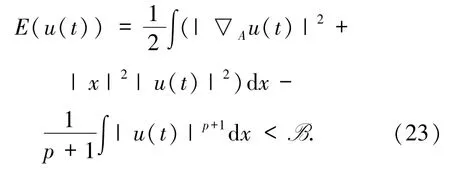
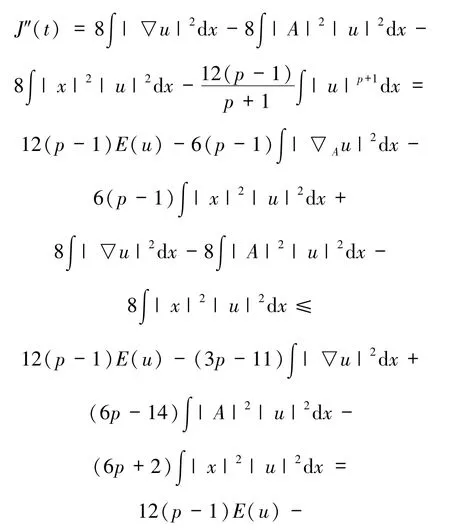
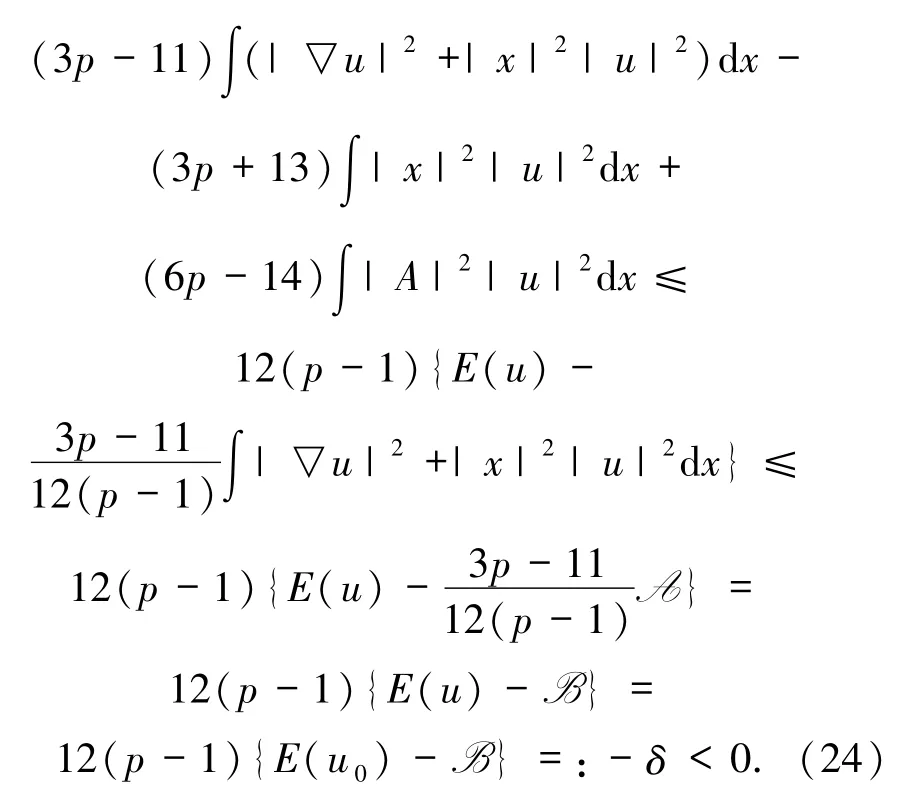
通過(guò)引理2.1 和文獻(xiàn)[19]知方程（1）的解 u（t，x）在有限時(shí)間內(nèi)爆破.證畢.

通過(guò)定理1.1的證明1）可以看出，當(dāng)1＜p＜5時(shí)方程（1）關(guān)于初值u0的整體解依然存在.