非自治Reaction-Diffusion方程的后向緊吸引子的正則性
佘連兵,張文林,李揚榮
(1.六盤水師范學(xué)院數(shù)學(xué)與信息工程學(xué)院,貴州六盤水553004; 2.西南大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,重慶400715)
眾所周知,拉回吸引子的緊性對研究非自治動力系統(tǒng)的長時間行為起著重要作用[1-5],但這類緊性是一種片段緊性的研究,和自治系統(tǒng)相似,并沒能展現(xiàn)出非自治系統(tǒng)對時間依賴的獨特性.
最近,文獻(xiàn)[6]對非自治動力系統(tǒng)所產(chǎn)生的拉回吸引子的后向緊性(對于過去時間的并是緊的)做了研究,并建立了完善的存在性理論,該理論指出,若系統(tǒng)具有一個單調(diào)遞增的有界的拉回吸收集且系統(tǒng)是后向漸近緊的,則系統(tǒng)存在唯一的后向緊拉回吸引子,從此拉回吸引子的后向緊性的研究受到了廣泛關(guān)注.文獻(xiàn)[7-8]分別建立了非自治3D Navier-Stokes方程和非自治波動方程產(chǎn)生的非自治動力系統(tǒng)的后向緊吸引子的存在性定理;文獻(xiàn)[9]運用能量的方法、高低頻分解、Sobolev嵌入的方法獲得了具有弱耗散非自治Schr?dinger后向緊吸引子的存在性;文獻(xiàn)[10]建立了有界域上非自治Reaction-Diffusion方程后向緊拉回吸引子的存在性定理;文獻(xiàn)[11]研究了非自治Reaction-Diffusion方程在RN上的拉回吸引子的后向緊性.本文主要考慮如下的非自治Reaction-Diffusion方程在Lp(Q)(p≥2)空間上的后向緊動力學(xué):

其中,λ>0,Q是RN中的有界域,f和g的假設(shè)條件將在后面給出.
首先,在外力項g是后向λ-緩增有限的假設(shè)條件下,證明了此方程生成的動力系統(tǒng)在Lp(Q)(p≥2)上有一個單調(diào)遞增的有界的拉回吸收集.其次,在g是后向絕對連續(xù)的假設(shè)條件下,運用一個后向截斷的方法證明了該動力系統(tǒng)在Lp(Q)(p≥2)上是后向漸近緊的,從而由文獻(xiàn)[6]的Theorem 2.9可知,非自治Reaction-Diffusion方程在 Lp(Q)(p≥2)上存在一個后向緊的拉回吸引子.
1 預(yù)備知識
設(shè)(X,‖·‖X)是一個Banach空間,X上有界集的全體記為 B(X).為 X 上的 Hausdorff半距離.
定義1.1設(shè) S(t,s):X→X,?t≥s是定義在X上的一族連續(xù)的映射,如果
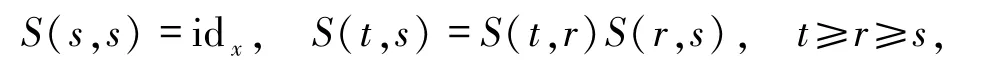
那么稱S是一個非自治的過程.
定義1.2若?t1,t2∈R,當(dāng) t1≤t2時,若 X 中非自治集 A={A(t)}t∈R滿足 A(t1)?A(t2),則稱A是單增的.
定義1.3設(shè) A={A(t)}t∈R是 X 中的一個非自治集,若滿足:
2)A具有不變性,即
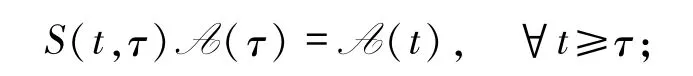
3)A具有拉回吸引性,即

則稱A是關(guān)于非自治過程S的一個后向緊吸引子.
為結(jié)果證明的需要,下面將引用文獻(xiàn)[6]中的一個判定性定理.
定理1.1若定義X上的一個非自治過程S(·,·)滿足:
(i)S(·,·)在X上存在一個單增的有界的拉回吸收集 K={K(t)}t∈R;
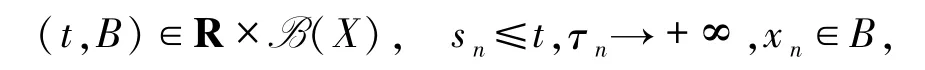
則S(·,·)存在一個后向緊拉回吸引子
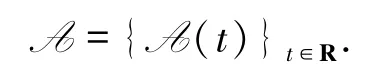
下面介紹后向Gronwall型不等式,其證明類似于文獻(xiàn)[4]的Lemma 3.3.
引理1.1后向Gronwall型不等式:設(shè)y、y1和y2是R上的局部非負(fù)可積函數(shù),且y′是R上的局部可積函數(shù),b≥0是一個常數(shù),若?t∈R,有

則對?t∈R,μ>0有

2 非自治Reaction-Diffusion方程存在唯一的后向緊拉回吸引子
考慮如下具有初邊值條件的非自治Reaction-Diffusion方程

其中,λ>0,Q是RN中的有界域,對 f和 g做如下假設(shè):
假設(shè) F設(shè) p >2,β1,β2,β3>0,f(·,·)∈C1(Q ×R,R)滿足:
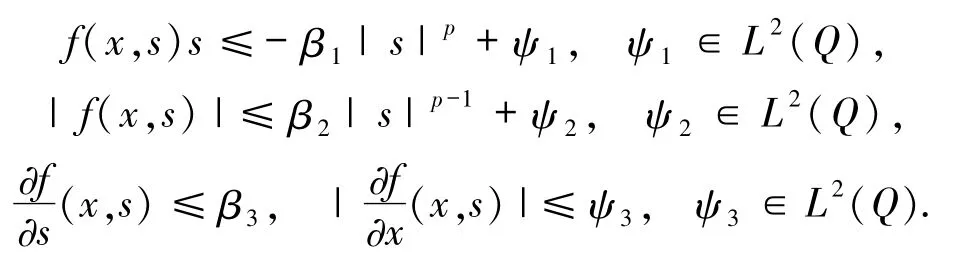
與文獻(xiàn)[6]中對非自治項的假設(shè)條件不同,假設(shè)如下:
假設(shè)G0.
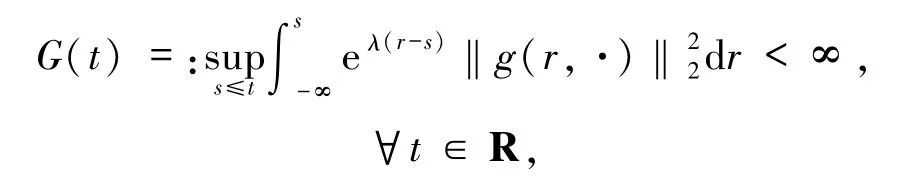
假設(shè)G1g是后向λ-緩增有限的,即其中,λ是方程(2)中給定的常數(shù),‖·‖p(p≥2)是 Lp(Q)的范數(shù).
假設(shè)G2g是后向絕對連續(xù)的,即
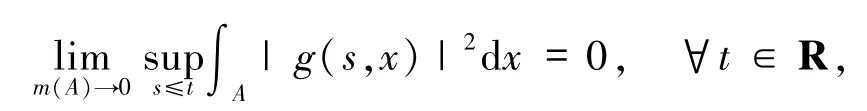
這里m(A)是集合A的勒貝格測度.
由文獻(xiàn)[12]知,對?s∈R,方程(2)在假設(shè) F和假設(shè)G0下是適定的,即存在唯一的連續(xù)解

且此解關(guān)于初始值u0是連續(xù)的,故可定義如下的非自治過程
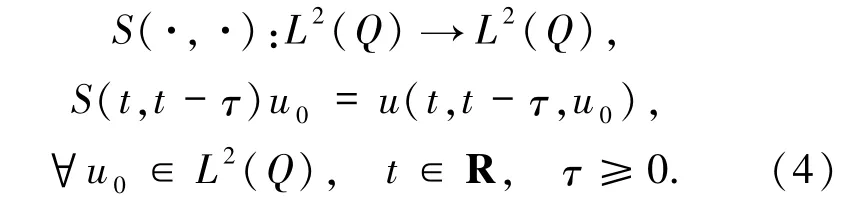
2.1 后向一致吸收性與后向截斷估計先在Lp(Q)上做一個后向一致估計,為了簡化計算,設(shè)c是變化的正常數(shù).
引理2.1若假設(shè)F和假設(shè)G0、G1滿足,則對于每個(t,B)∈R ×B(L2(Q)),存在一個

使得
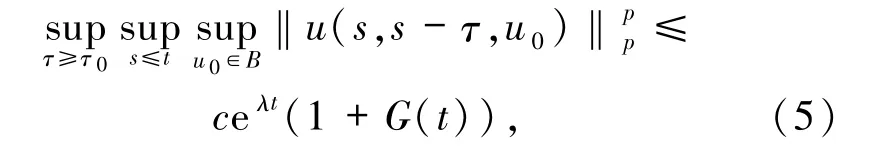
其中G(t)由假設(shè)G1給出.




2.2 本文主要結(jié)果
定理2.1若條件F和G0~G2成立,則非自治的Reaction-Diffusion方程(2)生成的過程(4),滿足:
(i)在Lp(Q)中有一個單調(diào)遞增的有界的吸收集 H={H(t)}t∈R;
(ii)S(·,·)在 Lp(Q)中是后向漸近緊的;
(iii)在Lp(Q)中有一個唯一的后向緊拉回吸引子 A={A(t)}t∈R.
證明(i)設(shè)
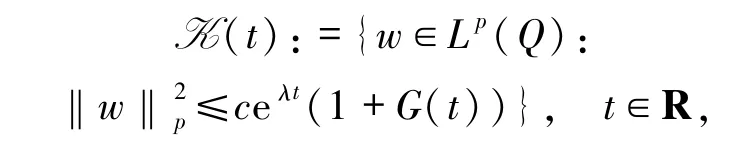
其中G(t)是假設(shè)G1中的一個增的有界的函數(shù),故由引理2.1知K 是 S(·,·)在 Lp(Q)上的一個增的有界的吸收集.
(ii)下面證明
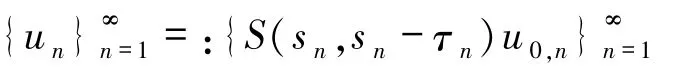
在Lp(Q)的拓?fù)湎掠幸粋€收斂子列,這里
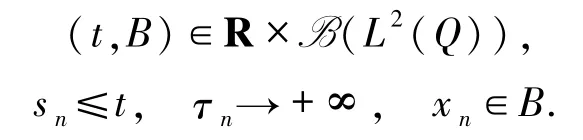
由引理2.2和 τn→ +∞可知存在 N1∈N和M>0使得
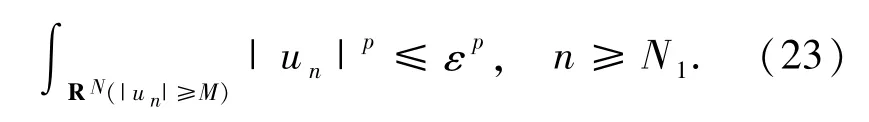
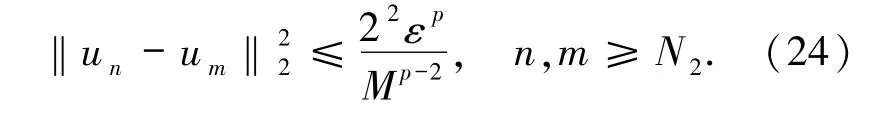
容易驗證
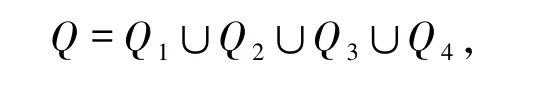
其中

由(24)式可知
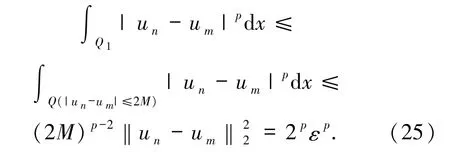
由(23)式可知:
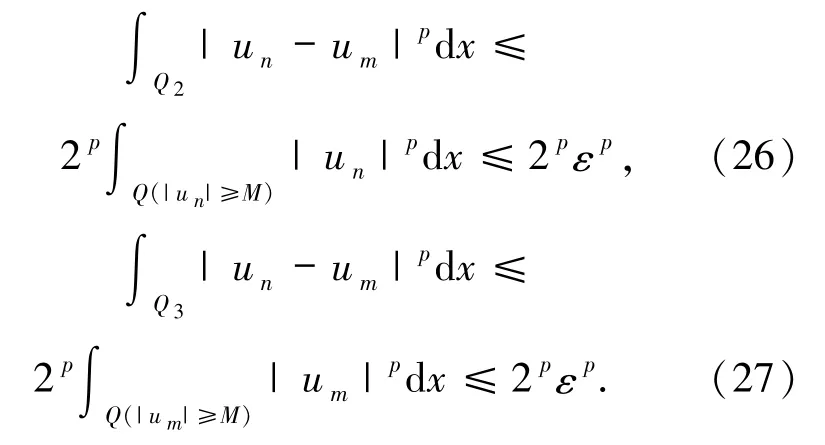
又由

和(23)式可知
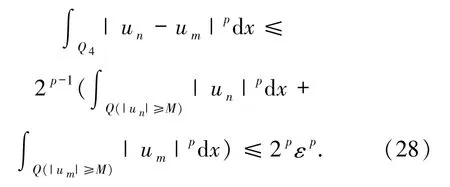
由(25)~(28)式可知

故由(i)和(ii)可知定理2.1的條件滿足,所以(iii)成立.
致謝六盤水師范學(xué)院校級項目(LPSSYKYJJ201801、LPSSYKJTD201907)對本文給予了資助,謹(jǐn)致謝意.

