一類隨機(jī)偏微分方程有限維約化的逼近
楊 敏,陳光淦*,李 琴
(1.四川師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,四川成都610066; 2.四川師范大學(xué)可視化計算與虛擬現(xiàn)實四川省重點實驗室,四川成都610066)
隨機(jī)不變流形為隨機(jī)偏微分方程驅(qū)動的動力系統(tǒng)提供了一個幾何結(jié)構(gòu)刻畫.Duan等[1-2]證明了一類隨機(jī)偏微分方程的隨機(jī)不變流形的存在性與光滑性.無窮維狀態(tài)空間使得方程解的研究工作非常復(fù)雜.Wang 等[3]和 Roberts[4]證明了不變流形若是幾乎處處漸近完備的,則可將無窮維系統(tǒng)約化到有限維.
Acquistapace等[5]證明了處處連續(xù)處處不可微的W(t)可由處處連續(xù)且可微的Φε(t)逼近,其中Φε(t)的定義見第2 節(jié).Jiang 等[6]證明了帶光滑噪聲的隨機(jī)系統(tǒng)的穩(wěn)定流形可近似帶不光滑噪聲的隨機(jī)系統(tǒng)的穩(wěn)定流形.Wang等[7]應(yīng)用Wong-Zakai逼近理論證明原系統(tǒng)可由簡化的隨機(jī)系統(tǒng)去逼近.
考慮一類帶乘性高斯白噪聲驅(qū)動的隨機(jī)發(fā)展方程

其中A、W、F 將在第 2節(jié)給出,“?”是 Stratonovich意義下的乘積,且系統(tǒng)(1)通常乘積意義下的形式為

本文研究由處處連續(xù)處處可微的Φε(t)驅(qū)動的隨機(jī)發(fā)展方程

證明了系統(tǒng)(3)的有限維約化收斂到系統(tǒng)(1)的有限維約化.
1 預(yù)備知識
令空間H是一個實值可分的Hilbert空間,其范數(shù)為|·|,內(nèi)積為〈·〉,線性算子A是H上C0半群{etA}的生成元.W(t)是標(biāo)準(zhǔn)的實值布朗運(yùn)動,F(xiàn)是H上的非線性函數(shù)滿足 F(0)=0和Lipschitz條件
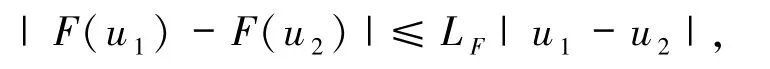
其中LF>0是Lipschitz常數(shù).
假定σ(A)為算子A的譜,令

其中σc是一個有限的集合,且
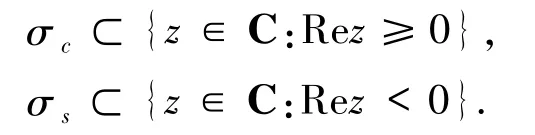
在空間H上做一個A不變分解,使得分別限制在 Hc和 Hs空間上的算子 Ac=A|Hc和 As=A|Hs,且滿足

這里 H=Hc⊕Hs,Hc是一個有限維空間,且{etAc}是Hc上的解半群.假定存在常數(shù)α、β滿足0≤α<β,使得

給定完備概率空間(Ω,F(xiàn),P),在Ω上定義映射流 θ={θt}t∈R:R ×Ω→Ω.如果映射{θt}t∈R滿足條件:
(i)θ0=id,
(ii)對任意的 s,t∈R,有 θtθs=θt+s,
則稱(Ω,F(xiàn),P,θ)為測度動力系統(tǒng)[1].
如果映射
是(B(R)×F×B(H),F(xiàn))-可測,且滿足
(i)φ(0,ω,x)=x,
(ii)φ(t+s,ω)=φ(t,θsω,φ(s,ω)),s,t∈R,ω∈Ω,x∈H,
則稱測度動力系統(tǒng)θ和φ構(gòu)成的二元組(θ,φ)為隨機(jī)動力系統(tǒng).
考慮Langevin方程


定義
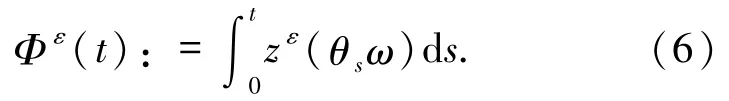
引理1.1[5]設(shè) W(t)是 R 上的布朗運(yùn)動.任給一個時間 T >0,則當(dāng) ε→0 時,Φε(t)→W(t)在[0,T]上是幾乎處處一致的.
引進(jìn)變換 T(ω,x)=xe-εzε(ω),系統(tǒng)(1)轉(zhuǎn)化為
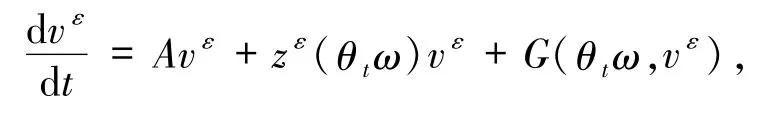

其中

顯然函數(shù)G和F有相同的Lipschitz常數(shù)LF.
引理1.2[1]假設(shè) vε是系統(tǒng)(7)的解,那么
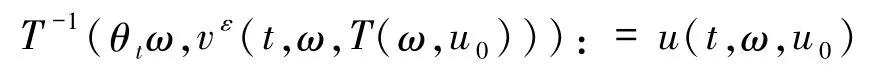
是系統(tǒng)(1)的解,其中T-1是T的逆變換,且

定義1.1假設(shè)M(ω)是隨機(jī)動力系統(tǒng)φ(t,ω)的不變流形.如果對任意的 x∈H存在 y∈M(ω),使得
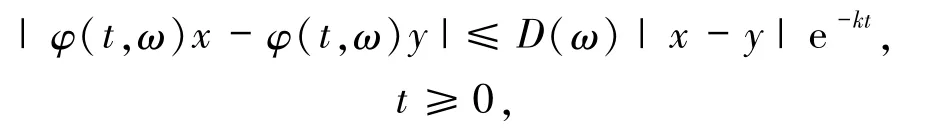
對幾乎所有的ω∈Ω成立,那么稱不變流形M(ω)是幾乎處處漸近完備的,其中D(ω)是一個正的隨機(jī)變量,k是一個正常數(shù).
定義1.2給定一個正的隨機(jī)變量δ,定義隨機(jī)集合
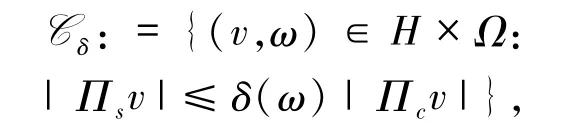
則 Cδ(ω)(ω)={v:(v,ω)∈Cδ}被稱作隨機(jī)錐,這里投射算子 Πc:H→Hc,Πs=I- Πc:H→Hs,且 I是恒等算子.
定義1.3對于一個隨機(jī)錐 Cδ(ω)(ω),如果存在一個隨機(jī)變量≤δ,使得對幾乎所有的ω∈Ω都滿足
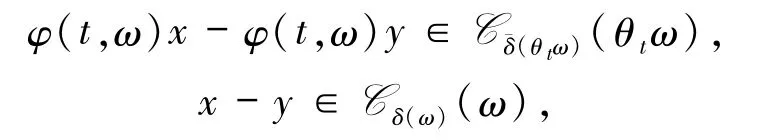
那么這個隨機(jī)動力系統(tǒng)φ(t,ω)被稱為有錐不變性,其中
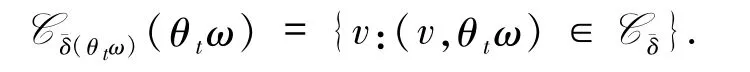
下面給出本文一些所用符號說明.記φ(t,ω)、φε(t,ω)分別為系統(tǒng)(7)和(3)在空間(Ω,F(xiàn),P,θ)上的隨機(jī)動力系統(tǒng),且

其中符號 Υ 代表{u,vε,Xε,U,V,Y}中任意元素.這里Πc、Πs如定義1.2中所給的投射算子.
2 有限維約化
假設(shè) vε和 Xε分別為系統(tǒng)(7)和(3)的解,其初值分別為任給 η∈(-β,-α),定義2個Banach空間
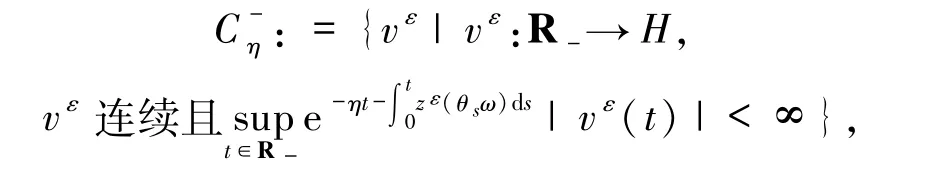
其范數(shù)為

以及

其范數(shù)為
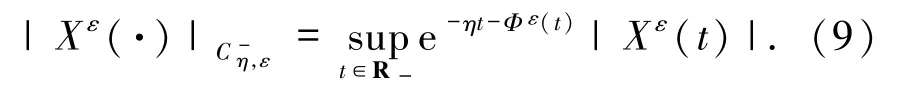
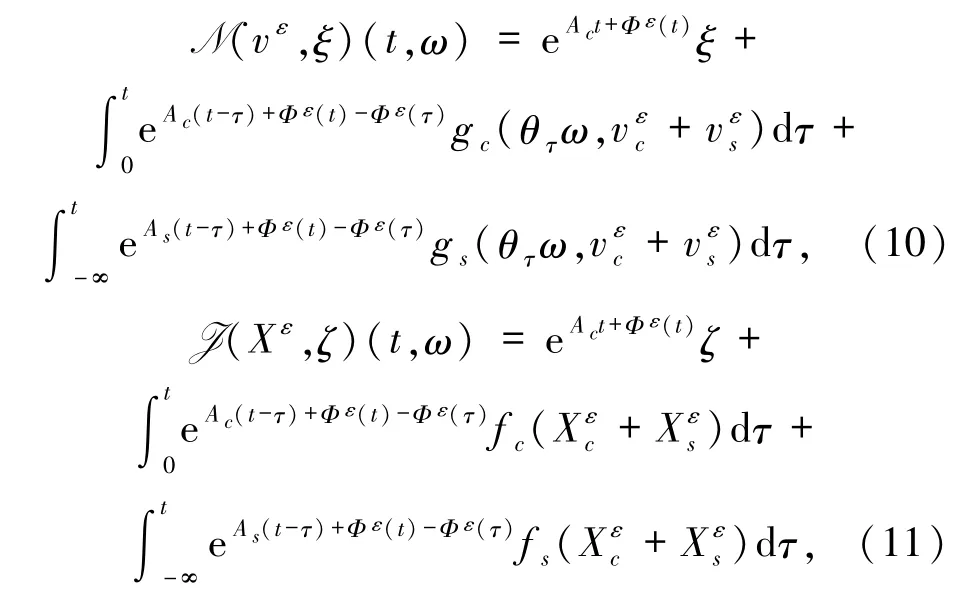
引理2.1[2,6]如果 LF滿足條件

那么隨機(jī)系統(tǒng)(7)和(3)分別有Lipschitz不變流形
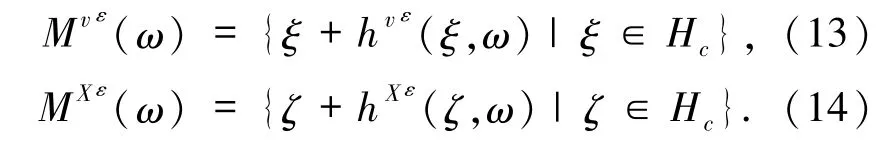
進(jìn)一步,取值于 Hs的 Lipschitz連續(xù)映射 hvε和 hXε滿足

命題2.1[3](i)如果(12)式成立,那么存在一個正的隨機(jī)變量D(ω)和一個正常數(shù)k,使得對于隨機(jī)系統(tǒng)(7)的任意解 vε(t,θ-tω),都存在一個軌道 V(t,θ-tω)∈Mvε(ω)滿足
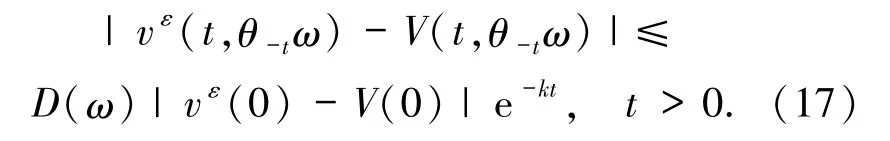
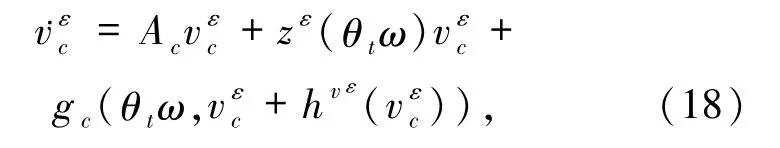
注2.1由引理1.2,系統(tǒng)(1)的軌道u=(uc,us)可約化到有限維空間Hc上且滿足
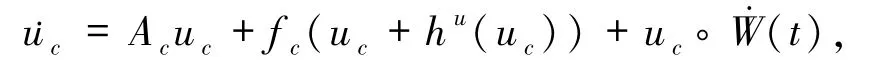
其中

進(jìn)一步,軌道 U=(uc,hu(uc))被稱為系統(tǒng)(1)依賴于不變流形 Mu(ω)={ξ+hu(ξ)|ξ∈Hc}的解.
由文獻(xiàn)[3],如果給定最終時間 Tf>0,則在t∈[0,Tf]時,系統(tǒng)(7)分別限制在空間 Hc和 Hs的解為

其中
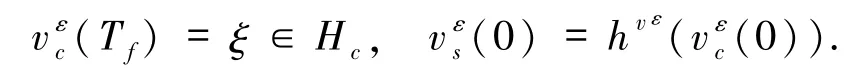
同理可得系統(tǒng)(3)分別限制在空間Hc和Hs的解為

其中
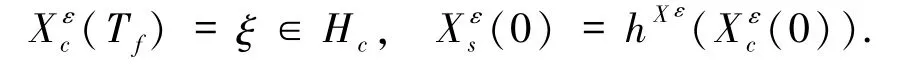
引理2.2[1]若(12)式成立,則對任意的 Tf>0,(19)式有唯一解且(20)式有唯一解進(jìn)一步,對任意 t≥0,有

引理2.3[1,3](i)如果(12)式成立,那么系統(tǒng)(3)的隨機(jī)動力系統(tǒng) φε(t,ω)具有錐不變性.
(ii)如果存在 t0>0,使得任意的 x,y∈H,φε(t0,ω)x- φε(t0,ω)y?Cδ(θt0ω),那么

其中,D(ω)是緩增的隨機(jī)變量,
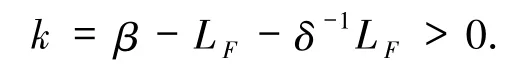
命題2.2(i)如果(12)式成立,那么存在一個正的隨機(jī)變量D(ω)和一個正常數(shù)k,使得對于隨機(jī)系統(tǒng)(3)的任意解 Xε(t,θ-tω)都存在一個軌道 Y(t,θ-tω)∈MXε(ω)滿足


證明任給ω∈Ω,討論系統(tǒng)(3)的解


有

其中β+η>0,且記
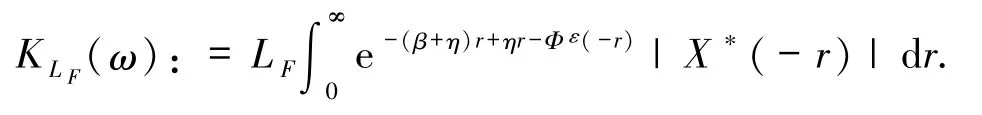
根據(jù)錐不變性有
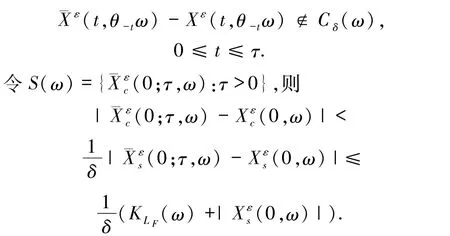
因此,對幾乎所有的ω∈Ω,S(ω)是Rn空間上的一個有界集.選一個序列τm→∞使得

其中Y(ω)是可測的.令

且滿足初值
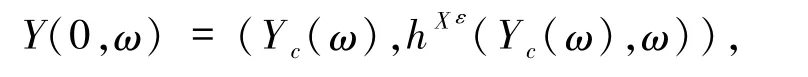
則 Y(t,θ-tω)∈MXε(ω),且
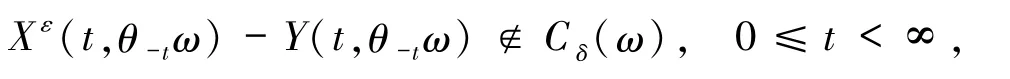
即 MXε(ω)幾乎處處漸近完備,(21)式得證.
由(i)可知 Y(t,θ-tω)∈MXε(ω),且 MXε(ω)幾乎處處漸近完備,由文獻(xiàn)[3]的方法,則可約化到有限維空間 Hc上,且,命題2.2 得證.
3 有限維上的逼近
引理3.1假設(shè)是系統(tǒng)(7)和系統(tǒng)(1)的有限維約化,則對幾乎所有ω∈Ω有

證明由引理1.2,有,且當(dāng) ε→0 時,則此時

引理3.1得證.
引理3.2假設(shè)是系統(tǒng)(7)和系統(tǒng)(3)的有限維約化,則對幾乎所有ω∈Ω有
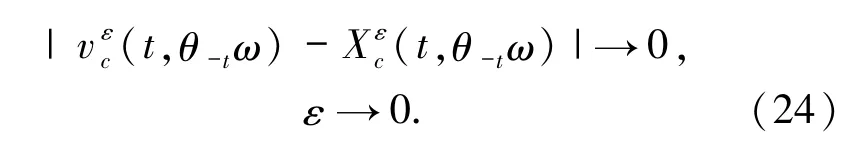
證明由(19)~ (20)式和 Φε(t)的定義,則對任意的 t∈[0,Tf]有


定理3.1假設(shè)是系統(tǒng)(3)和系統(tǒng)(1)的有限維約化,則對幾乎所有ω∈Ω有
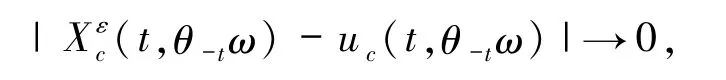

由引理3.1和3.2,定理3.1顯然成立.
致謝四川師范大學(xué)2019年研究生優(yōu)秀論文培育項目(201903-10)對本文給予了資助,謹(jǐn)致謝意.

