有序Banach空間非線性分數階邊值問題的正解

李小龍

（隴東學院數學與統計學院，甘肅慶陽745000）

0 引言

分數階微分方程在自然科學、工程技術和控制系統等領域有著廣泛的應用，近年來許多學者應用相關的不動點定理與上下解的單調迭代技巧研究了分數階邊值問題的正解及其多個正解的存在性[1-10]，但在一般的Banach空間中對該類問題的研究還比較少.

設E為有序Banach空間，其正元錐P為正規錐，正規常數為 N，記 I=[0，1].本文將在一般的有序Banach空間E中討論非線性分數階邊值問題

Banach空間的微分方程與普通微分方程的最大差異是把微分方程轉換為與之等價的積分方程后，相應的積分算子不再具有緊性.為了對該積分算子應用凝聚映射的不動點定理，通常需要給非線性項f附加一些非緊性測度條件.本文使用了如下非緊性測度條件：

（H0）對?R ＞0，f（I× PR）有界，且存在常數使得對?t∈I，D?PR，有α（f（t，D））≤Lα（D），其中，Γ（·）為 Gamma函數，

在研究Banach空間中微分方程正解的文獻中，文獻[7]要求f在有界集上一致連續.文獻[11]利用新的非緊性測度估計技巧，只在f連續的情形下獲得了問題（1）的正解，并將文獻[8]的結果推廣到了無窮維空間.

1 預備知識

定義1[1]設 α ＞0，函數 f：（0，+∞）→R 的 α階Riemann-Liouville積分為

其中Γ（·）為Gamma函數.

定義2[1]設 α ＞0，函數 f：（0，+∞）→R 的 α階Riemann-Liouville導數為

其中，Γ（·）為 Gamma函數，n=[α]+1.

由Riemann-Liouville型微分的定義，有以下討論.

引理1[1]設 α ＞0，假設 u∈C（0，1）∩L（0，1）是分數階微分方程的解，則 u（t）具有如下形式，ci∈R，i=1，2，…，N，其中 N 是大于或等于 α 的最小正整數.

引理2[1]假設 u∈C（0，1）∩L（0，1）有 α ＞0階導數屬于 C（0，1）∩L（0，1），則

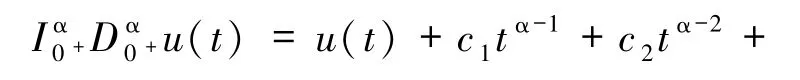
其中N是大于或等于α的最小正整數.

引理3[2]設 3 ＜ α≤4，則對?h∈C（I，E），Banach空間E中的線性分數階邊值問題

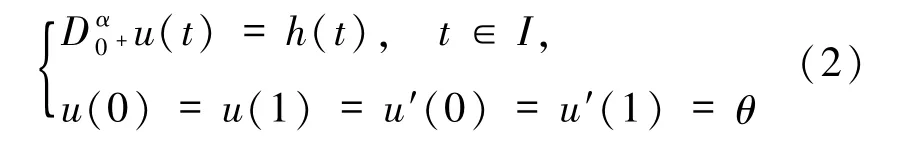
存在唯一解

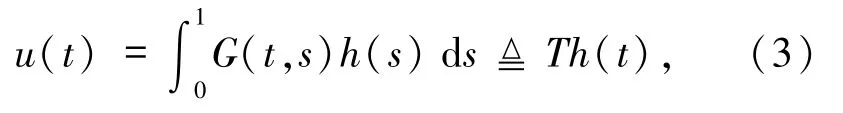
其中

引理4由（3）式定義的算子 T：C（I，E）→C（I，E）滿足.

證明由（3）式知

故

從而

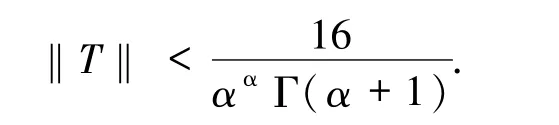
由文獻[7]中引理3.2 知，算子 T：C（I，E）→C（I，E）為正的線性連續算子，T有相應第一特征值λ1的正特征函數 u*，即 λ1Tu*=u*.文中 E與C（I，E）中有界集的 Kuratiwski非緊性測度均由α（·）表示.對 B?C（I，E），記 B（t）=｛u（t）｜u∈B｝?E，t∈I.

引理5[12]設 B?C（I，E）為等度連續的有界函數族，則α（B（t））在I上連續，且

引理6[13]設 B=｛un｝?C（I，E）為可列集，若存在 ψ∈L1（I）使得‖un（t）‖≤ψ（t），a.e.，t∈I，n=1，2，…，則 α（B（t））在 I上可積，且

引理7[11]設D?E有界，則存在D的可列子集 D0，使得 α（D）≤2α（D0）.

定義算子 Q：C（I，P）→C（I，P）如下：

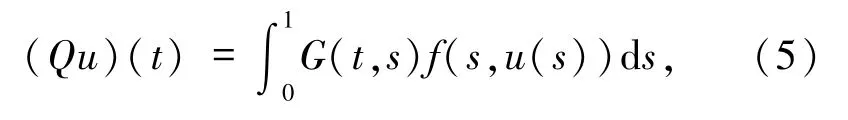
則 Q：C（I，P）→C（I，P）連續，且方程（1）的解等價于積分算子Q的不動點.

引理8設 f：I×P→P 滿足（H0），則由（5）式定義的算子 Q：C（I，P）→C（I，P）為凝聚映射.

證明易見Q把C（I，P）中的有界集映為有界的等度連續集.任取非相對緊的有界集B?C（I，P），下證 α（Q（B））＜α（B）.令 R=sup｛‖u‖｜u∈B｝，則對 ?t∈I，B （t）? PR，設為假設（H0）中的非緊性測度常數.由引理7知，存在可列集 B1=｛un｝?B，使得α（Q（B））≤2α（Q（B1））.故對?t∈I，由引理6 及假設（H0），有

因為Q（B1）等度連續，由引理5知

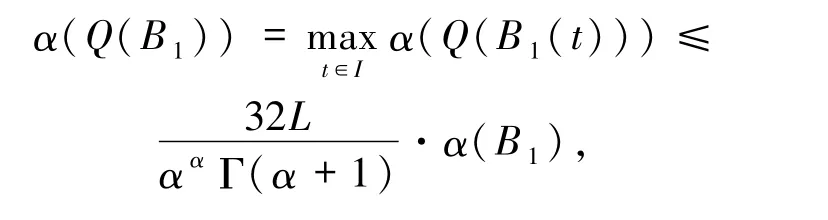
于是有

因此 Q：C（I，P）→C（I，P）為凝聚映射.

取 C（I，P）的子錐：

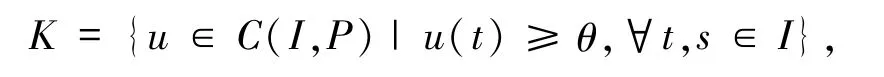
易證 Q（C（I，P））?K.因此，當 f：I× P→P 時，Q：K→K為凝聚映射，方程（1）的正解等價于Q在K中的不動點.本文將用凝聚映射的不動點指數理論尋找Q的不動點.

引理9[14]設E為Banach空間，K為E中的錐，Ω?E 為有界開集，θ∈Ω，Q：K∩→K 為凝聚映射，若 Q 滿足 u≠λQu，?u∈K∩?Ω，0 ＜ λ≤1，則不動點指數 i（Q，K∩Ω，K）=1.

引理10[15]設E為Banach空間，K為E中的錐，Ω?E為有界開集，Q：K∩→K為凝聚映射，若存在 υ0∈K，υ0≠θ，使得 Q 滿足 u-Qu≠μυ0，?u∈K∩?Ω，μ≥0，則不動點指數 i（Q，K∩Ω，K）=0.

2 主要結果及其證明

定理1設E為有序Banach空間，其正元錐P為正規錐，f：I×P→P 連續，滿足條件（H0）.若 f滿足下列條件之一：

（H1）1）存在及δ＞0，使得當 x∈Pδ時，f（t，x）≤εx；

2）存在 η ＞λ1及 h0∈C（I，P），使得當 x∈P時，f（t，x）≥ηx-h0（t）.

（H2）1）存在 ε ＞λ1及 δ＞0，使得當 x∈Pδ時，f（t，x）≥εx；

則邊值問題（1）至少存在一個正解.

證明下證由（5）式定義的凝聚映射Q：K→K存在非零的不動點.取0＜r＜R＜∞，記Ωr=｛u∈K｜‖u‖ ＜r｝，?Ωr=｛u∈K｜‖u‖ =r｝.分2 種情形證明當r充分小R充分大時Q在上存在不動點.

情形1f滿足假設（H1）.取0＜r＜ δ，其中 δ為假設（H1）中的常數，證明Q滿足引理9中條件：

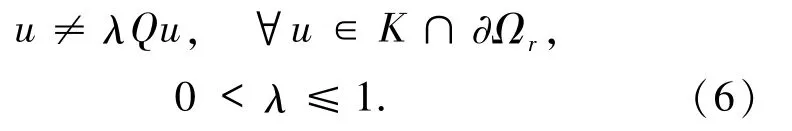
反設（6）式不成立，那么存在 u0∈K∩?Ωr及 0＜λ0≤1，使得 u0=λ0Qu0.按 Q 的定義及條件（H1）的1）得

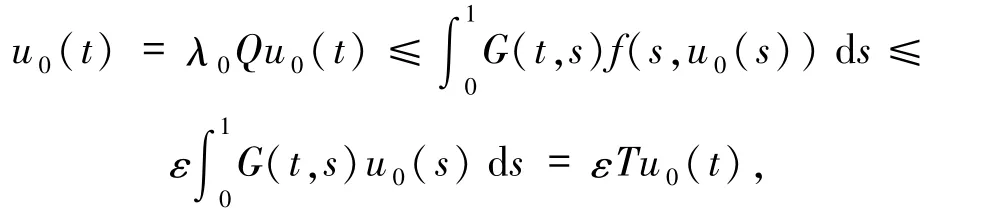
累次使用上式，則有

由錐K的正規性和引理4有

故有‖u0‖ =0，這與 u0∈K∩?Ωr（‖u0‖ =r）矛盾.于是（6）式成立，故由引理9知

下證當R充分大時有

反設存在 u0∈K∩?ΩR及 τ0≥0，使得 u0-Qu0=τ0u*，則按算子Q的定義及條件（H1）的2）得

從而有

又 η ＞λ1知（ηT-I）為正算子，故逆算子（ηTI）-1存在，由錐K的正規性得

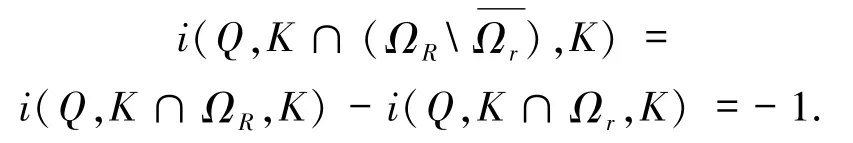
情形2f滿足假設（H2）.取0 ＜r＜δ，證明

反設（10）式不成立，則存在 u0∈K∩?Ωr及 τ0≥0，使得u0-Qu0=τ0u*，則u0=Qu0+τ0u*≥τ0u*，令，即，且 u0≥ τ*u*.又由 T的正性知，λ1Tu0≥τ*λ1Tu*=τ*u*.

由條件（H2）的1）有

這與τ*的定義矛盾.故由引理10知

再證當R充分大時有

假設存在u0∈K及0＜λ0≤1，使得u0=λ0Qu0.

從而由條件（H2）的2）得

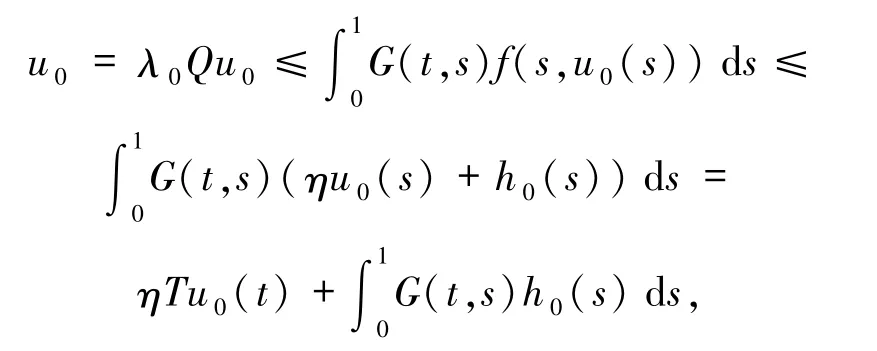
即

又

則

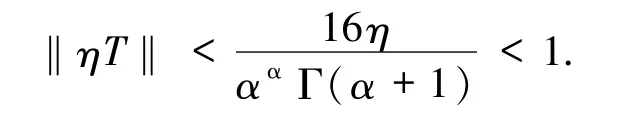
由微擾定理知，I-ηT存在有界逆算子（I-ηT）-1，且

從而由錐K的正規性得

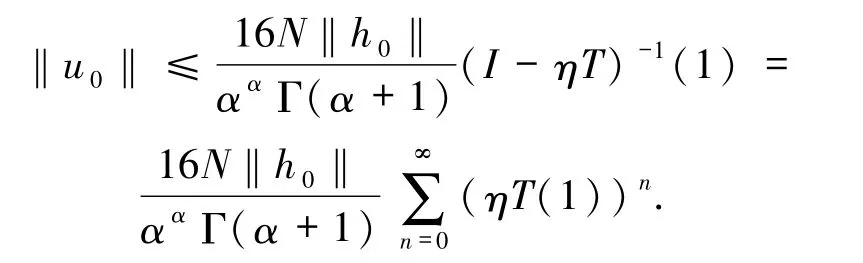
取 ε0＞0，使得

則有

則有

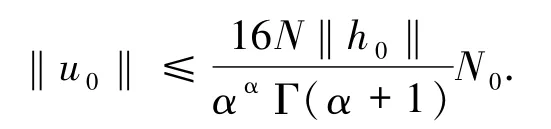
由引理9知 i（Q，K∩ΩR，K）=1，于是該式結合（11）式有