武漢市2019-nCoV新型冠狀肺炎預測模型分析

侯文濤，李 磊

(運城學院 數學與信息技術學院，山西 運城 044000)

引言

2019新型冠狀肺炎，即2019-nCoV，是目前新發現的又一種可以在人與人之間傳染的冠狀病毒，首次發現于2019年武漢病毒性肺炎病例中。新型冠狀病毒主要的傳播方式是呼吸道飛沫傳播和接觸。2019年12月，湖北省武漢市在展開的流感及相干疾病監測中，發現多起病例感染病毒性肺炎，現被證實為新型冠狀病毒感染，之后新冠肺炎感染者數量開始在武漢市內急劇上升，后確定該病毒具有人傳人風險，隨之中國其他地區也出現感染者，同時全世界大多數國家都出現了感染病例，引發全球的重視。目前，新型冠狀肺炎是世界眾多學者關注和研究的重點問題之一。顏銘江利用改進的SEIR模型預測疫情的進一步發展，計算每日有效再生數的變化，預測在2020年4月19日所有的患者將全部出院，累計確診患者為66487[2]；蔡潔構造SEIR模型模擬武漢市新冠肺炎的發展趨向，得出疫情的“拐點”將會出現在采取封城方法后的第35天，同時預測疫情在4月底將會根本得到控制[3]；朱仁杰以SIR模型為基礎，對7個國家疫情的發展情況進行預測，并剖析各國減少接觸率等防治措施對疫情發展的影響，揭示了各國的防疫現狀以及減少接觸率的措施的重要；王思遠采用SEIR模型預測2019-nCOV疫情數據，有效的預估了疫情發展趨勢，并根據新的數據不斷自動更新未來疫情發展[5]；林挺葵結合Holt兩參數指數平滑模型預測疫情的未來發展趨勢，結果表明在現有高效防控措施下，粵西地區及各地級市新冠肺炎疫情正在停止惡化，有望在2月底出現“拐點”[6]。本文在參考已有文獻的基礎上，結合所學統計預測方法[7]，對收集的武漢新型冠狀疫情的日增長數據構建Holt雙參數指數平滑模型與求和自回歸移動平均ARIMA模型，并選擇較優模型預測武漢2月11日至13日新型冠狀疫情的新增感染人數，對武漢新冠肺炎疫情的預防控制提供理論支持，為新冠疫情的研究提供新的參考。

1. 理論方法

1.1 Holt兩參數模型

指數平滑法的基本思想就是預測值是以前觀測值的加權和，并且對不同的數據賦予不同的權數，越接近預測期的數據給予越大的權數，越遠離預測期的數據賦予越小的權數；基本公式為

St=a*xt+(1-a)st-1

式中St為時間t的平滑值；xt為時間t的觀測值；St-1為時間t-1的平滑值；α為平滑參數，其取值范圍為[0，1]。Holt雙參數線性指數平滑法[8]是將趨勢序列直接進行平滑，對原序列進行預測的，因此平滑公式為

St=axt+(1-α)(St-1+rt-1，

rt=β(St-St-1)+(1-β)rt-1，

式中{St}為修勻后的預測序列；xt為時間t的觀測值；α，β為平滑參數，其取值范圍為[0，1]。{rt}為趨勢序列，需要注意的是趨勢序列{rt}也是一個隨機序列。預測公式為

Pt+l=St+l*rt

式中Pt+l為時間t向前l期的預測值；l為向前預測的期數[10]。

1.2 ARIMA模型

ARIMA模型[9]，中文名稱為求和自回歸移動平均模型。是由美國統計學家博克思(Box)和詹金斯(Jenkins)在20世紀70年代初提出的一種時間序列的預測方法。ARIMA(p，d，q)模型具有如下結構

式中{εt}為零均值白噪聲序列。ARIMA建模流程圖如圖1所示。

1.3 模型評價

在利用模型擬合數據時不可避免地會存在誤差，那么模型對實際值擬合的程度便稱為擬合優度，擬合優度的統計量稱為可決系數或者確定系數(R2)，計算公式為

圖1 ARIMA建模流程圖

2. 實證分析

本文所使用的數據來源于2020年1月16日至2月16日中國衛生健康委官方網站(http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml)[11]和中國湖北省衛生健康委官方網站(http://wjw.hubei.gov.cn)[12]所公布的數據。

使用R軟件繪制2020年1月16日至2月10日武漢地區新型冠狀病毒的日增長人數時序圖，該序列呈現出明顯的上升趨勢，隨著時間天數的增加，日增感染人數保持正值，感染人數持續上升，詳見圖2。

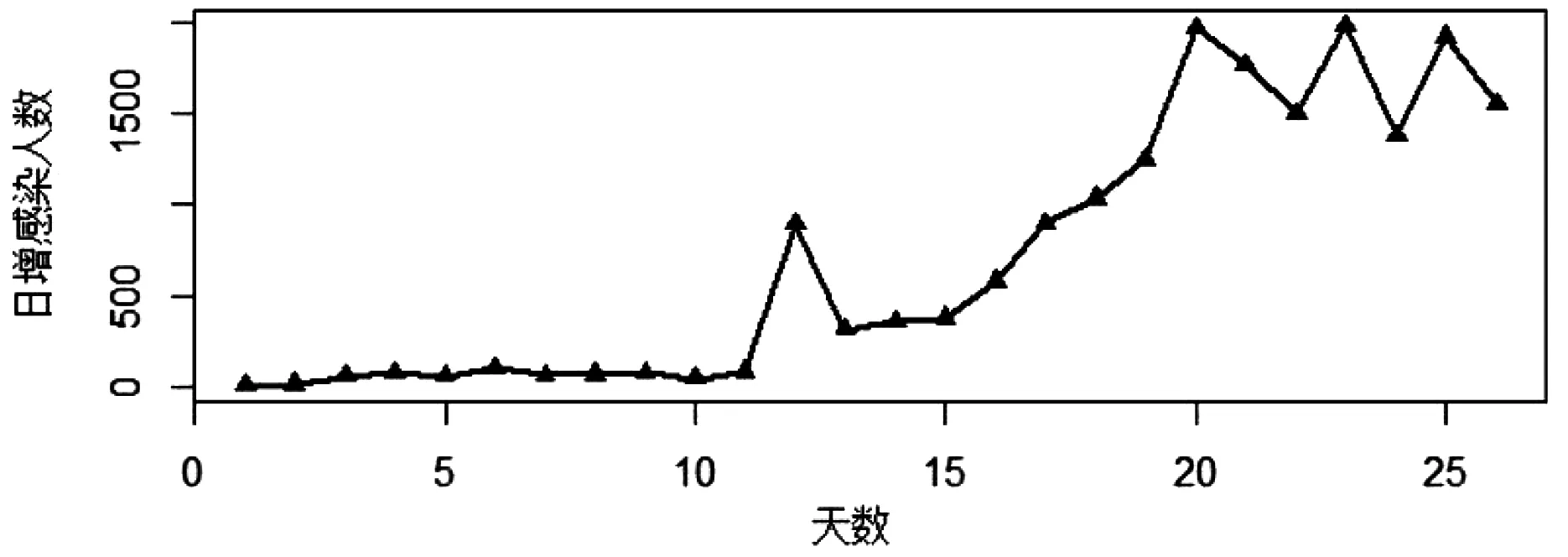
圖2 武漢新冠肺炎每日新增感染人數時序圖

2.1 Holt模型在武漢市新冠肺炎的應用

借助R語言3.6.2，將數據進行簡單處理之后讀入序列，建立Holt雙參數平滑模型，經過反復實驗得到Holt雙參數平滑系數α=0.57，β=0.06，詳見表1。說明修勻后的預測序列{St}在未來預測中，近期數據對預測數據的影響比較大；趨勢序列{rt}在未來預測中，近期數據對預測數據的影響比較小；此時模型的誤差平方和達到最小，擬合的指數平滑模型為

通過采取以上一系列技術和管理措施，解決了盾構穿越高鐵橋梁樁基施工難題，確保了高鐵橋梁和車輛運行安全和隧道工程實體質量。本工程的施工經驗，也應用到了盾構下穿鐵路站場路基施工中，對將來其他類似工程施工具有一定的參考借鑒作用。

St=0.57xt+0.43(St-1+rt-1)

rt=0.06(St-St-1)+0.94rt-1

預測模型為

Pt+l=1696.91+l*59.47

表1 Holt雙參數模型系數表

通過預測模型Pt+1=1696.91+l*59.47，計算1月16日至2月10日的估計值，并考慮該模型預測結果的滯后性，結果如表2。將真實值與估計值繪制在一張圖中，如圖3，圖中黑色實線表示真實值，紅色虛線表示估計值，可以看出兩條曲線在前期幾乎重合，動態趨勢也基本吻合，Holt雙參數線性指數平滑模型對新增感染人數擬合效果很好。

表2 Holt雙參數線性指數平滑法計算結果表

圖3 Holt雙參數線性指數平滑模型擬合圖

2.2 ARIMA模型在武漢新型肺炎的應用

2.2.1 序列平穩化

由圖2可知，序列呈現曲線上升趨勢，是非平穩序列。對序列進行二階差分，差分后的序列進行單位根檢驗，其中P=0.02182，小于顯著性水平0.05，序列趨于平穩。詳見表3。

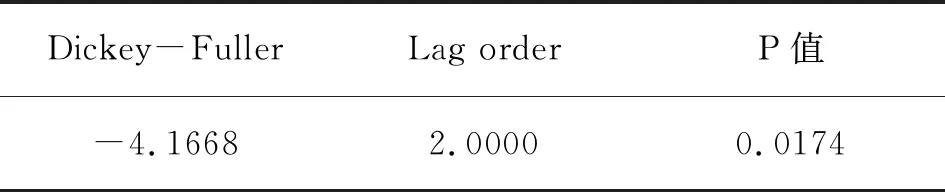
表3 平穩性檢驗表

alternative hypothesis:stationary

將差分后的序列延遲6期、延遲12期、延遲18期分別進行白噪聲檢驗，，結果如表4，其中P值均小于顯著性水平0.05，序列是非白噪聲序列。

表4 ARIMA模型白噪聲檢驗表

建立ARIMA(p,2,q)模型，使用R軟件，將p、q的可能取值0、1、2進行由低階向高階進行測試，并依據AIC最小準則，經過反復實驗，得出當p=1,q=1時，AIC值最小，所以ARIMA(1,2,1)模型為最優模型，故序列采用ARIMA(1,2,1)模型進行擬合，詳見表5。

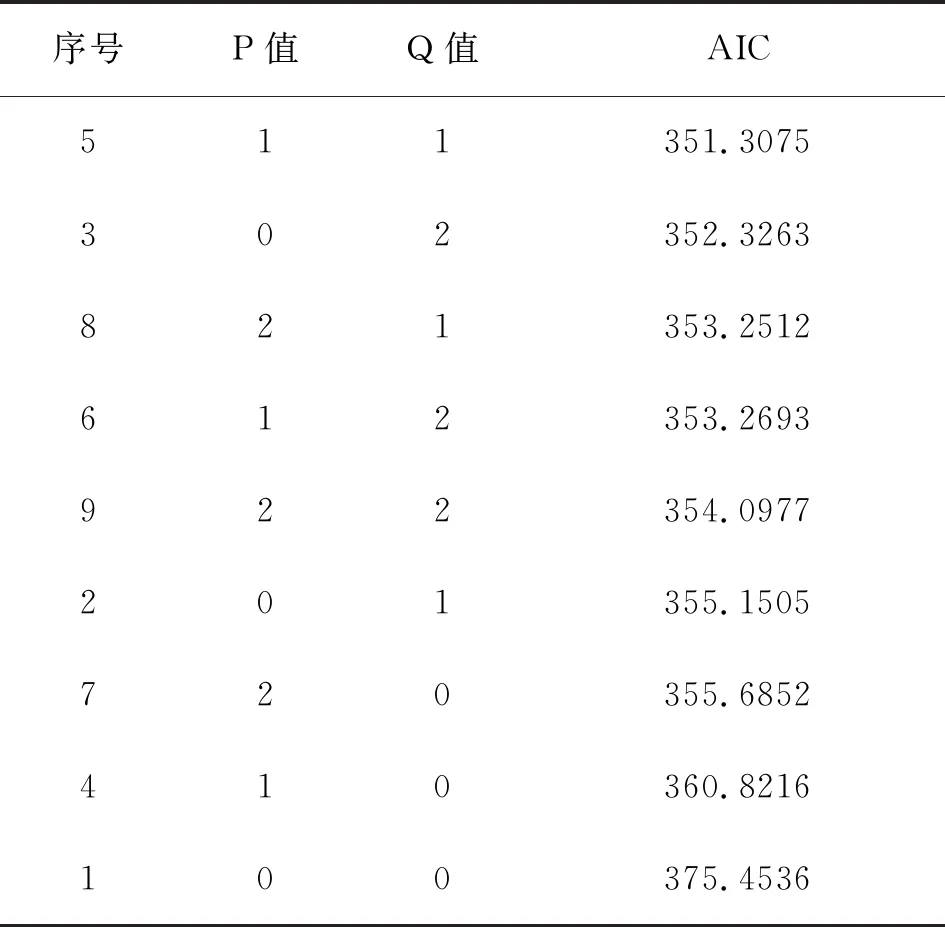
表5 ARIMA模型AIC值計算表

2.2.3 參數估計與模型檢驗

利用ARIMA(1,2,1)模型對序列進行擬合，并估計模型參數，模型的口徑為:

Xt=-0.4759Xt-1+qt-qt-1;εt～N(0,87009

對模型的系數進行檢驗，P值均小于顯著性水平0.05，表明模型ARIMA(1,2,1)中所有的系數都通過了t檢驗，建立具有統計學意義。詳見表6。

表6 ARIMA模型系數表

對ARIMA(1,2,1)模型的殘差進行LB檢驗，結果顯示ARIMA(1,2,1)模型的殘差序列為白噪聲序列，說明模型殘差部分是由隨機因素造成的，信息已充分提取，滿足ARIMA的前提假設。詳見表7。

表7 ARIMA(1,2,1)模型白噪聲檢驗表

通過ARIMA(1,2,1)模型計算1月16日至2月10日的估計值，詳見表8。如圖4，將真實值與估計值繪制在一張圖中，圖中黑色實線表示實際值，紅色虛線表示估計值，可以看出兩條曲線在前期幾乎重合，動態趨勢也基本吻合，ARIMA(1,2,1)模型對新增感染人數擬合效果也很好。

表8 ARIMA模型計算結果表

2.3 預測分析

分別計算兩個模型的可決系數R2，Holt雙參數指數平滑模型的可決系數為0.968,ARIMA(1,2,1)模型的可決系數為0.834,Holt雙參數指數平滑模型的擬合程度更好。

圖4 ARIMA模型擬合圖

選用擬合度較好的Holt模型對武漢2月11日到2月13日新冠肺炎每日新增感染人數做出預測，并結合實際值進行對比。詳見表9，繪制真實值和預測值的折線圖，詳見圖5。因2月12日至2月13日的數據中含有臨床值感染人數數據，本文除去了臨床值對研究的影響。模型預測值顯示，武漢2月11日至13日新型冠狀肺炎的日感染人數持續增加。但結合實際日感染人數，實際值普遍低于預測值。由此可知，之前一段時間的疫情防治措施已經初步取得成效，疫情爆發期已經過去，開始進入穩定期[13]。

從實際數據分析，武漢疫情的發病數據整體呈現先上升后下降的趨勢，在2月13日達到最大值。1月16日到2月13日之前，日感染人數呈現上升趨勢，2月13日之后，日感染人數呈現下降趨勢。直到3月18日之后，日感染人數接近于0。利用Holt模型對武漢日感染人數進行預測，并于實際值比較，分析得出武漢疫情的穩定期已經到來，對于整體把握新型冠狀疫情的走勢具有重要意義。

表9 Holt雙參數指數平滑模型預測結果表

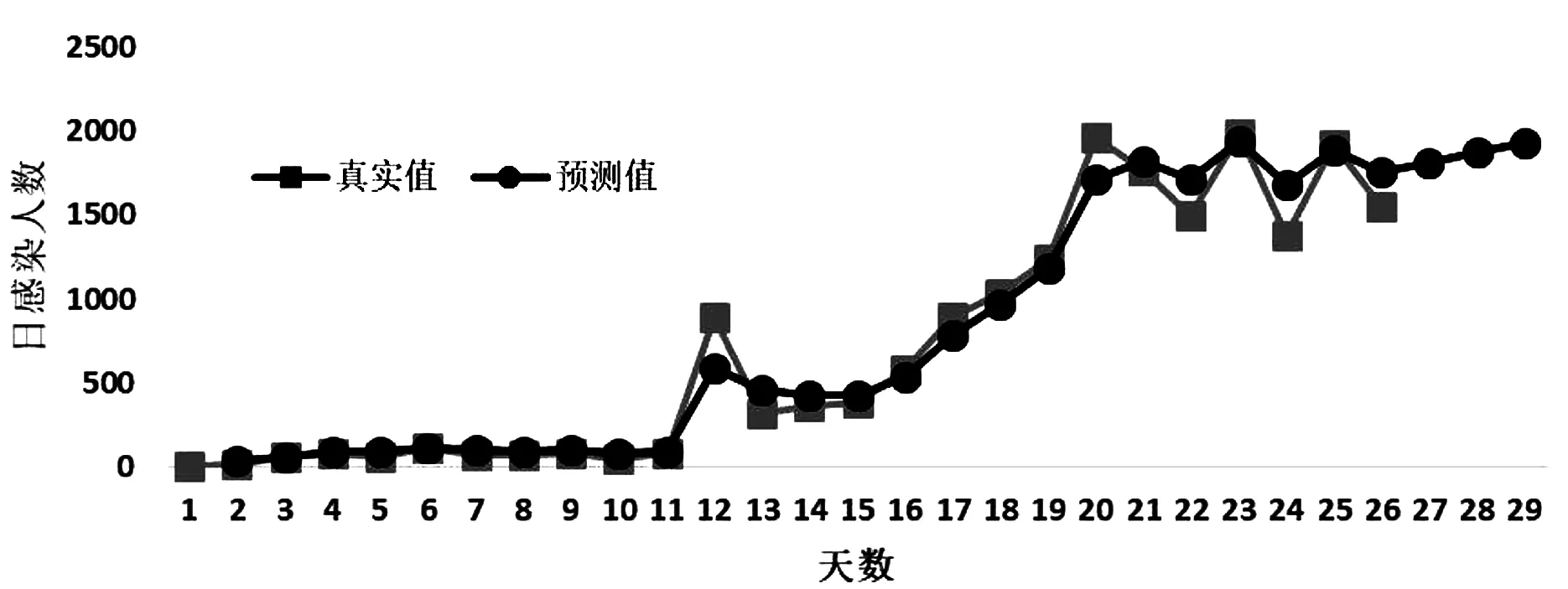
圖5 Holt雙參數指數平滑模型預測圖

3. 小結

新型冠狀病毒自今年爆發以來，席卷多個國家，在全球范圍內造成了不可估計的損失，是我國乃至世界面臨的最嚴重的流行疾病問題之一。建立有效的統計預測模型預測新冠肺炎的發病情況，對新冠肺炎的預防和研究具有重要意義。本文利用2020年1月16日至2月13日國家衛生健康委員會和湖北省衛生健康委員會發布的新冠肺炎數據，分別建立了Holt雙參數線性指數平滑模型和ARIMA(1,2,1)模型。其中，ARIMA模型的擬合系數為0.834，Holt雙參數線性指數平滑模型的擬合系數為0.968，Holt雙參數線性指數平滑模型的擬合效果較優。最后，使用模型對2月11日至2月13日的新增感染人數做出預測，實際值低于預測值，與武漢疫情發病數據先上升后下降的整體變化趨勢相吻合。研究表明在疫情爆發期前一段時間的疫情防治措施已經初步取得成效，人們的防疫意識也明顯增強。證明之前的封城和居家隔離措施是正確有效的，接下來仍然需要努力，使得疫情的“拐點”早點到來。