基于演化博弈論的機動車碳稅政策研究
許 杰,劉國平
(桂林電子科技大學建筑與交通工程學院,廣西 桂林 541004)
近些年來,隨著經濟的發展,私家車的數量呈爆發式增長。據統計,截至2019年年底,全國汽車保有量達2.6億量,全國66個城市汽車保有量超過百萬輛。由中國移動源環境管理年報公布2013-2018年,全國汽車保有量增長83.9%,但污染物排放量僅下降4%[1]。由機動車排放溫室氣體及污染物造成的大氣污染成為我國各大城市發展亟需解決的問題。我國政府通過提高機動車排放標準、發展新能源汽車等措施控制污染物的排放,實施搖號購車、尾號限行、擁堵收費等措施限制機動車的使用。但這些措施并不能從根本上解決機動車污染物排放問題。而部分OECD國家已經通過實施機動車碳稅政策來控制機動車的排放污染,包括英國、德國、美國、加拿大、法國等[2]。征收碳稅具有可操作性強,覆蓋面廣,公平的優勢,能夠有效遏制機動車碳排放,并引導居民使用低碳方式出行,自覺承擔生態保護的責任。然而我國碳稅制度尚未健全,僅在全國發電行業及大型碳排放企業推廣實施[3]。因此,為促進我國機動車碳減排、增強公眾綠色出行意識,研究機動車碳稅政策對居民出行的影響,對控制機動車碳排放和推動綠色低碳發展具有重要意義。
從目前國際實際例子來看,機動車碳稅政策主要包括個人碳交易和征收碳稅兩類[4]。而國外實施機動車碳稅的經驗能否應用到我國,而我國政府又該如何實施機動車碳稅政策來控制機動車的碳排放增長,這已成為當前亟需解決的問題。國內部分學者通過構建經濟模型來探究碳稅征收政策,如方文詩[5]依據CGE建模理論,構建了交通碳稅CGE模型和汽車行業碳稅模型,并仿真模擬了不同的碳稅征收方式。李峰、王文舉[6]從公平性角度探究機動車碳稅,合理配置差幅補貼能夠在公平性層面改善居民收入分配情況。袁玲子[7]在基于湘潭地區私家車車主的調查,運用Logistical模型分析了車主承擔碳稅意愿的因素。許妙玲[8]對機動車碳稅稅率測算進行研究。還有些學者對碳稅政策方式進行了探討,魏慶坡[9]通過對相對減排目標和絕對減排目標兩者與碳稅的兼容性進行分析,提出相對減排目標下碳交易和碳稅兼容。趙立祥、吳松嶺[10]利用動態最優化、效用函數、實驗經濟學等相關理論建立經濟模型,研究比較了超大城市私家車的碳稅政策和個人碳交易政策。符淼、孫宇[11]運用TREMOVE中國模型和中國國家數據,模擬新的車船稅政策和碳稅政策在我國的實施。現有的諸多研究都論證了機動車碳稅政策能夠有效控制機動車碳排放增長,達到減排目的。實施碳稅過程中并非只靠一方努力就能實現,需要考慮政府管理部門與居民之間的合作。而考慮實施碳稅過程中如何協調各方主體間的利益來最大化碳減排目標的研究較少。
演化博弈論能夠研究主體決策間的影響,通過復制動態分析研究主體策略演化的過程。目前在政府的決策實施、環境治理措施中廣泛應用。有徐瑩等[12]構建政府與交通企業的演化博弈模型,分析第三方舉報率、監管成功率對政府策略選擇的影響。焦建玲等[13]在碳減排獎懲機制下構建地方政府和企業群體行為的演化博弈模型,分析影響演化穩定的因素。劉長玉、廈同水等人[14]基于低碳視角,建立了政府與制造商之間的決策行為的演化博弈模型,分析了兩者達到均衡所需條件的差異。國外有Aerts、Cormier[15]、Kathuria[16]、Liu[17]運用演化博弈理論研究政府與企業的關系,分析各自行為及均衡策略。劉枚蓮[18]通過構建演化博弈模型,從前景理論視角分析了地方政府監督下的企業低碳生產策略。現有演化博弈理論的應用,還未有針對機動車碳稅實施過程中政府與居民決策的分析應用。
鑒于此,本文采用演化博弈理論和Matlab仿真分析的方法,構建政府管理部門與居民的演化博弈模型,研究實施機動車碳稅過程中,各方主體決策行為的演化博弈趨勢以及達到理想狀態的條件。為政府管理部門制定政策控制機動車碳排放增長提供相應的理論基礎,同時也為綠色環保、低碳減排型社會的演化提供有益借鑒。
1 演化博弈模型的構建
1.1 博弈主體
主體是指指在博弈過程中擁有決策權的參與者,稱之為主體。本文研究機動車碳稅政策,為緩解因尾氣帶來的環境污染,政府管理部門采取積極的政策引導居民出行方式的改變。博弈主體為政府管理部門與居民,并假設兩者均為有限理性且以自身利益最大化為目標。
1.2 博弈策略
策略是指各主體在博弈過程中采取的行動方案。政府管理部門有“實施機動車碳稅政策”和“不實施機動車碳稅政策”兩種選擇策略,設選擇實施政策的概率為。居民有“低碳方式出行”與“非低碳方式出行”兩種選擇策略,設選擇低碳出行的概率為。策略集合見表1。
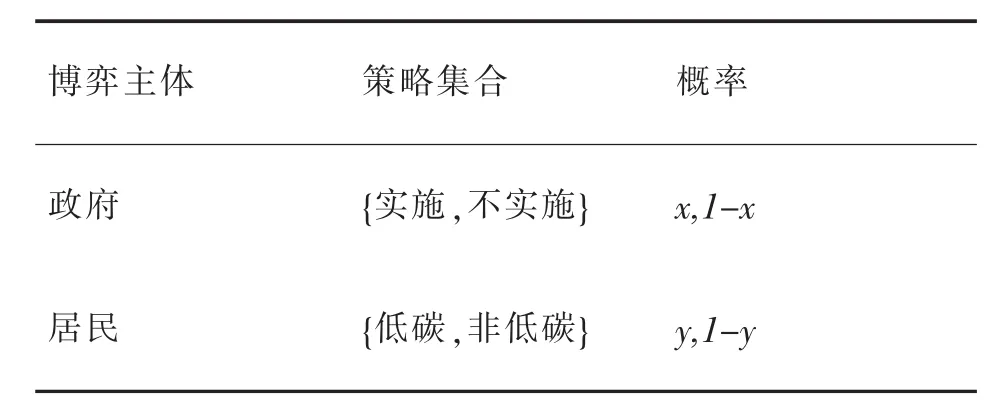
表1 博弈主體策略集合及概率
1.3 博弈收益
收益指各主體做出決策,在博弈完成后產生的期望滿意度。而研究各主體在不同策略下的收益,參照劉加伶[19]、王桂鵬[20]、徐建中[21]等研究中的博弈參數,并根據本文研究內容進行適當改進。
政府管理部門在控制機動車碳減排過程中,通過實施機動車碳稅,以車輛購置時一次性繳納稅款和燃料碳稅的形式征稅,征的稅款為P。同時需要投入相應的管理成本M,用于碳稅系統的建立、設備的購置以及人員的培訓。征得的稅款可以增加公共交通基礎設施建設的投入H,補貼居民購買新能源汽車等,提高居民低碳出行的舒適性與便利性,這部分投入為。當政府管理部門采取積極有效的政策降低機動車碳排放,交通出行產生的溫室氣體得到有效的控制,政府管理部門將獲得環境收益G。同時也得到公眾的認可,使得政府管理部門的影響力與公信力得到提升,這部分的收益為U。居民選擇非低碳方式出行,政府管理部門將增加投入環境治理的費用N。
居民選擇低碳方式出行,例如使用更清潔環保的汽車、乘坐公共交通等,獲得的預期收益為A。同時低碳方式出行帶來機動車尾氣排放的降低、大氣污染的減少,居民將獲得精神與健康上的收益T。居民選擇非低碳方式出行將獲得預期收益B,而實際中使用私家車出行帶來的便利與收益要遠大于低碳出行,即B>A。見表2。

表2 博弈參數說明
基于上述參數得到演化博弈的收益支付矩陣,見表3。

表3 政府管理部門與居民的支付矩陣
2 演化博弈穩定性及演化路徑分析
2.1 復制動態方程
政府管理部門的博弈策略:

居民的博弈策略:
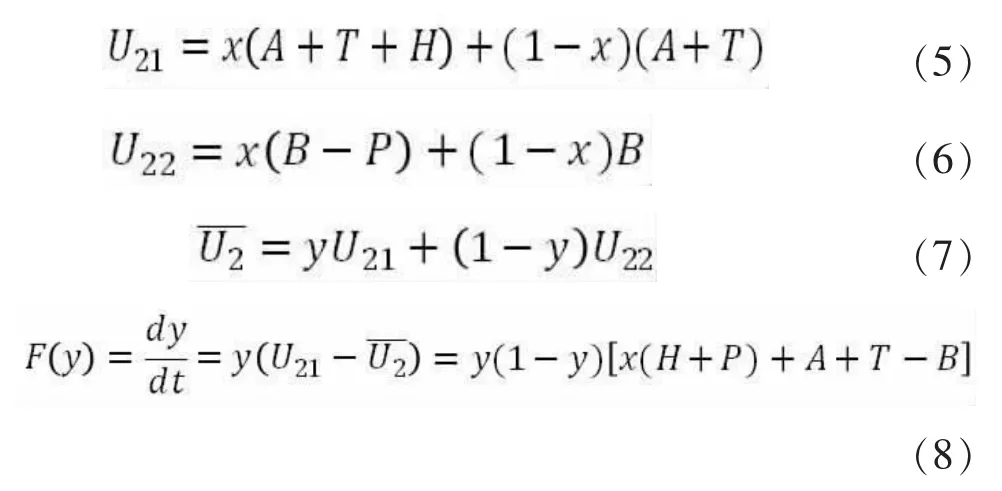
2.2 復制動態分析
復制動態是指隨著時間的推移,博弈主體通過學習與模仿,根據對方的策略行為不斷調整自己策略。
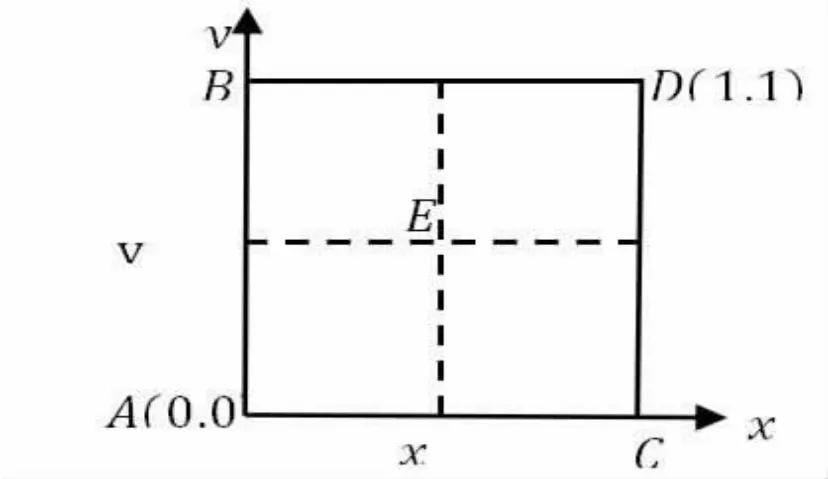
圖1 動態均衡點坐標
在分析雙方的演化路徑過程中,通過對每個復制動態方程求導,觀察一階導數的方向來進行穩定策略的判斷。

根據演化博弈的特征可知,政府管理部門與居民在博弈過程中,最終的策略選擇總是基于最佳的結果。而復制動態的原理是在有限博弈方組成的群體中,結果更好的策略會被更多的博弈方所選擇,從而使得采用相應策略的博弈方比例發生變化。所以利用復制動態方程根據不同效益條件下的策略分析,可以確定最終行為選擇策略。
(1)政府管理部門的復制動態分析
情形 1:根據式(4),若 y(-P+M)+P+U-M-H=0,即,則f(x)恒等與0,此時行為決策達到穩定狀態,不會隨著時間推移而改變。
情形 2:若 y(-P+M)+P+U-M-H>0,即 y<y*。令f(x)=0,則x=0,x=1是x的兩個均衡點,將兩點帶入式(9)可得,所以x=1是平衡點。表明政府管理部門實施機動車碳稅政策的收益大于不實施,且實施過程中的收益大于管理成本與對公共交通建設投入之和。此時選擇實施機動車碳稅是政府管理部門的演化穩定策略。
情形 3:若 y(-P+M)+P+U-M-H<0,即 y>y*,則f’(0)<0,f’(1)>0,所以 x=0 是平衡點。表明政府管理部門實施機動車碳稅政策的收益小于不實施,且實施過程中的收益不抵管理成本與對公共交通建設的投入。此時選擇不實施機動車碳稅是政府管理部門的演化穩定策略。
(2)居民的復制動態分析
情形 1:根據式(8),若 x(H+P)+A+T-B=0,即,則f(y)恒等與0,此時行為決策達到穩定狀態,不會隨著時間推移而改變。
情形 2:若 x(H+P)+A+T-B>0,即 x>x*,令 f(y)=0,則y=0,y=1是y的兩個均衡點,將兩點帶入式(10)可得 f’(0)>0,f’(1)<0,所以 y=1 是平衡點。表明居民低碳方式出行的收益大于非低碳方式出行。此時低碳出行是居民的演化穩定策略。
情形 3:若 x(H+P)+A+T-B<0,即 x<x*,則 f’(0)<0,f’(1)>0,所以 y=0 是平衡點。表明居民低碳方式出行的收益小于非低碳方式出行。此時非低碳出行是居民的演化穩定策略。
2.3 穩定性分析
根據Friedman的判定原則對(0,0),(0,1),(1,0),(1,1),(x*,y*),五個均衡點進行穩定性分析。首先對微分方程組(4)和(8)依次求關于x和y的偏導數,分析系統的Jaconbian矩陣的局部穩定性。

根據上述雅可比公式可以得知,
J的行列式:

J的跡:

當滿足 detJ>0,trJ<0 這兩個條件,均衡點是演化穩定策略(ESS)。政府管理部門與居民演化博弈系統的五個均衡點分析結果見表4。

表4 政府管理部門與居民演化博弈穩定性分析結果
根據表4的均衡點分析可以得到:均衡點A表示,政府實施機動車碳稅政策過程中,管理成本與對公共交通基礎設施建設的投入大于征收的稅款與公信力提升帶來的收益。居民非低碳方式出行的預期收益要大于低碳方式出行的預期收益與健康改善的收益之和。此時政府與居民的策略最終趨向(0,0),即政府不實施機動車碳稅政策和居民選擇非低碳方式出行。均衡點B表示,政府實施機動車碳稅政策過程中,對公共交通基礎建設的投入與對居民低碳出行的補貼之和大于實施政策帶來公信力提升的收益。居民低碳方式出行的預期收益與健康改善帶來的收益之和大于非低碳方式出行的預期收益。此時政府與居民的策略最終趨向(0,1),即政府不實施機動車碳稅政策和居民選擇低碳方式出行。均衡點C表示,政府實施機動車碳稅政策過程中,征得的稅收及公信力提升帶來的收益大于管理成本與對公共交通基礎建設的投入之和。居民選擇非低碳方式出行,繳納完碳稅后的收益依然大于低碳方式出行的預期收益、政府給與的補貼與健康改善帶來的收益之和。此時政府與居民的策略最終趨向(1,0),即政府實施機動車碳稅政策和居民選擇非低碳方式出行。均衡點D表示,政府實施機動車碳稅政策獲得公信力提升的收益大于對公共交通基礎設施建設的投入及對居民低碳方式出行的補貼。居民低碳方式出行的預期收益、政府給與的補貼與健康改善帶來的收益之和大于繳納完碳稅后選擇非低碳方式出行的收益。此時政府與居民的策略最終趨向(1,1),即政府實施機動車碳稅政策和居民選擇低碳方式出行。
3 數值仿真實驗
為驗證演化博弈模型的可靠性,以便更加直觀的觀測模型的演化路徑,本文采用Matlab軟件對模型進行數值仿真分析。為使模型達到理性狀態(1,1),設定初始參數值 P=10,M=3,H=5,U=6,G=2,N=3,A=25,B=10,T=2。
3.1 x,y的變化對演化結果的影響
根據以上條件,先給定x的初始值為0.5,通過選取y的初始值,驗證x隨時間變化的影響,如圖2所示。由圖可知,y的初始值能夠影響x的收斂速度,且x最終會收斂于1,即政府管理部門選擇實施機動車碳稅政策。同理,再給定y的初始值為0.5,通過選取x的初始值,驗證y隨時間變化的影響,如圖3所示。由圖可知,x的初始值能夠影響y的收斂速度,且y最終會收斂于1,即居民選擇低碳方式出行。數值仿真的結果與前文所分析的演化結果一致,某一方的博弈策略選擇與收斂時間與另一方的策略初始比例有關。其中,居民選擇非低碳方式出行的比例越高,政府越容易實施機動車碳稅政策。同時實施機動車碳稅策略的初始比例提高,加快了居民選擇低碳方式出行策略的演化速度。

圖2 y變化下x的演化曲線

圖3 x變化下y的演化曲線
3.2 P與H的變化對演化結果的影響
給定x的初始值為0.5,y的初始值為0.5,通過改變P與H的值,驗證y隨時間變化的影響,如圖4、圖5所示。由圖4可知,增加對選擇非低碳方式出行的居民征收機動車碳稅,能夠加快居民選擇低碳方式出行的演化速度。由圖5可知,政府管理部門增加公共交通基礎設施建設的投入,對選擇低碳方式出行的居民提高補貼,能夠有效促進居民選擇低碳方式出行。

圖4 P變化下y的演化曲線
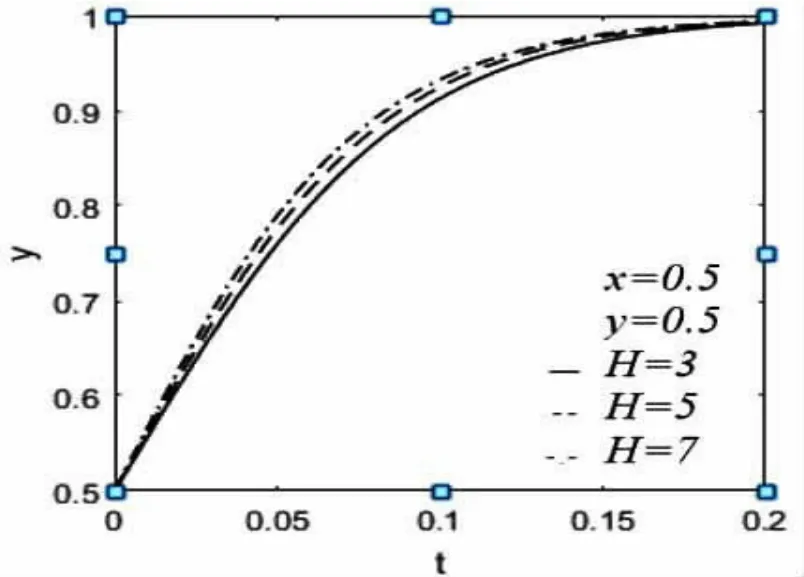
圖5 H變化下y的演化曲線
4 結論
本文研究了在機動車碳稅政策下由政府管理部門與居民組成的機動車碳減排系統,通過構建演化博弈模型,分析了各主體不同策略選擇下的演化結果及穩定性,并通過Matlab軟件仿真驗證,得到以下幾點結論。
1)在機動車碳稅實施過程中,政府管理部門與居民之間的決策相互影響。即政府管理部門選擇“實施機動車碳稅”的概率x受到y比例的影響。居民選擇 “低碳方式出行”的概率y受到x比例的影響。
2)實施機動車碳稅政策能夠有效促進居民選擇低碳方式出行。其中,政府管理部門征收碳稅P、對公共交通基礎設施建設的投入與對選擇低碳方式出行的居民給與的補貼H是實施效果的影響因素,且提高P與H的值能夠促進居民選擇低碳方式出行。
3)當演化條件滿足 U>H、H+A+T>B-P,最終系統會穩定在均衡點(1,1)。即政府管理部門公信力及影響力提升帶來的收益要大于對公共交通基礎設施建設的投入,居民選擇低碳方式出行的總收益大于非低碳方式出行,最終模型會演化成理想狀態。
由上述分析可得,為控制機動車碳排放增長,推動社會綠色低碳發展,需要政府管理部門與居民采取以下措施。
1)政府管理部門要制定合理完善的機動車碳稅征收制度,并利用互聯網等技術降低實施機動車碳稅政策的管理成本,提高管理效率。將所得稅收合理利用,增加對公共基礎設施的建設,提高居民低碳出行的便捷性與舒適性。通過補貼的形式,引導居民選擇低碳方式出行,構建低碳環保型社會。
2)提高居民的環保低碳意識,作為污染的生產者,每個人都應該承擔相應的義務。在對非低碳方式出行征收碳稅的同時,也要加大宣傳力度,引導居民養成低碳出行習慣。推動居民自覺承擔環境保護責任,主動為自己出行產生的碳排放繳稅。

