基于改進禁忌搜索算法的VRPSPDTW 研究

張 思，王 海 （上海大學 管理學院，上海 200444）

ZHANG Si， WANG Hai (School of Management, Shanghai University, Shanghai 200444, China)

0 引 言

近年來，隨著經濟水平的快速發展，人們的生活條件不斷改善，對生鮮產品的需求量逐年上升。據統計2018 年生鮮市場交易額約為1.91 萬億元，然而由于產品腐爛變質造成的損失高達1.23 千億元[1]。所以為了保證產品新鮮度從而降低貨損成本，運輸途中會全程低溫冷鏈，但這會大幅增加能耗成本。合理的車輛調度可以縮短產品的在途運輸時間，保證生鮮產品的新鮮度，降低貨損率，減少燃油消耗量，降低運輸成本。因此冷鏈物流的車輛路徑問題成為新的研究熱點，引起了眾多學者的關注[2]。

為了提高客戶滿意度，產品需要在規定的時間窗內交付客戶，然而由于生鮮產品的易腐性，因此客戶對產品新鮮度有一定要求，全程冷鏈降低了腐爛速度，但是會加大運輸油耗，產生更多的二氧化碳，不利于環境保護。現有的研究已經考慮了時間窗[3-5]、碳排放[6-8]、產品新鮮度[9-10]等多種情況下的冷鏈物流車輛路徑問題，但是在上述研究基礎上考慮同時取送貨情況下的冷鏈配送研究還相對比較少。生鮮產品要求在整個配送過程中保持恒定的低溫，車門的頻繁開關和裝載貨物時頻繁搬動會影響溫度控制，加速產品的腐爛變質；同時，生鮮產品的逆向物流量主要為包裝物的回收和少量缺陷產品的退貨，比一般產品少。將正向的配送和逆向的回收單獨運作，必然會增加制冷成本和運輸成本。因此，采用同時取送貨策略，可以節約運輸、制冷、回收等成本，有利于節約資源和保護環境。所以本文在前人的基礎上，考慮顧客同時有取貨和送貨的需求，建立帶時間窗的同時取送貨車輛路徑問題（Vehicle Routing Problem with Simultaneous Pickup-Delivery with Time Windows， VRPSPDTW） 運輸配送模型。

2003 年 Angelelli 等[11]首次提出 VRPSPDTW 問題，Savelsbergh[12]證明了 VRPTW （Vehicle Routing Problem with Time Windows） 為NP-hard 問題，那么它的拓展VRPSPDTW 也一定為NP-hard 問題。由于精確算法僅適用于求解VRPSPDTW 的小規模問題，而對于中大型規模，學者們更傾向于設計啟發式算法獲得最優可行解。Lai 等[13]應用改進的差分進化算法求解了一個8個顧客規模的算例。Wang 等[14]在Solomon[15]的VRPTW 測試算例的基礎上，提出了VRPSPDTW 的測試算例，并使用共同演化遺傳算法進行求解。該算例囊括了9 個中小型算例（顧客規模為10，25，50 各3 個） 和56 個大規模算例（顧客規模為100），成為國際上針對VRPSPDTW 的通用算例。Wang 等[16]采用并行模擬退火算法，王超等[17]應用離散布谷鳥算法，黃務蘭等[18]使用改進全局人工魚群算法都對該算例進行求解。

禁忌搜索算法（Tabu Search，TS） 是一種鄰域逐步尋優的局部搜索算法，采用禁忌策略減少循環搜索，提高搜索效率。李相勇[19]在對VRP 問題求解算法詳細綜述的基礎上指出，在各種啟發式算法中以禁忌搜索算法的求解質量最高，是一種高效算法。本文選用標準TS 作為算法框架，加入多種性能提升策略，提高算法的尋優能力，對VRPSPDTW 問題進行求解。

1 帶時間窗的同時取送貨車輛路徑問題

1.1 問題描述

冷鏈VRPSPDTW 可以被描述為：給定一個配送中心、一組位于不同位置的顧客以及一個冷藏車隊，每個顧客都有自己的服務時間窗以及取貨需求和送貨需求，管理者的決策是為車隊的每一輛車規劃服務顧客的行駛路徑，優化總的物流成本。

1.2 假設

一個配送中心為若干個顧客提供服務，配送中心和顧客的位置都是確定的，各顧客的取貨需求和送貨需求都是已知的，每輛冷藏車的起始點和終止點都是配送中心；配送中心的冷藏車數量充足且為同一型號；冷藏車輛在運輸過程中勻速行駛，不考慮交通情況的影響；每個顧客只允許被服務一次。

1.3 參數

（1） 集合。V 為顧客點集合，V=｛i ｝，i=1，2，…，n；i=0 表示配送中心，其中節點集合 U=V∪ ｛0 ｝；K 為冷藏配送車輛集合，K=｛k ｝，k=1，2，…，m。

（2） 參數。c1：每輛冷藏車的固定使用成本；c2：冷藏車行駛單位距離的運輸成本；c3：冷藏車提前到達客戶點處的單位時間等待成本；c4：冷藏車延遲到達客戶點處的單位時間懲罰成本；c5：冷藏車排放單位重量二氧化碳的成本；c6：單位重量制冷劑的使用成本；c7：單位重量貨物的損耗成本；Q：冷藏車的最大載重量；dij：客戶點i 與客戶點j 之間的距離；tij：從客戶點i 到客戶點j 所需的時間；pi：客戶點i 處的取貨需求量；qi：客戶點i 處的送貨需求量；ti：冷藏車在客戶點i 處裝卸貨所需的時間；f：燃料的消耗函數；σ1：運輸過程中消耗單位體積的燃料產生的二氧化碳重量；σ2：運輸過程中制冷設備單位時間內產生的二氧化碳重量；g1：運輸過程中產生的熱負荷函數；g2：裝卸貨過程中產生的熱負荷函數；α1：運輸過程中單位時間內單位貨物的損耗比例；α2：裝卸過程中單位時間內單位貨物的損耗比例； ［ETi，LTi］：客戶點i 的時間窗。

1.4 數學模型

1.4.1 碳排放成本

碳排放成本主要包括兩個方面：一是發動設備產生的CO2成本，二是制冷設備產生的CO2成本。

（1） 發動設備產生的碳排放成本。發動設備產生的CO2主要通過燃油消耗量來計算，依據參考文獻[20]，冷藏車單位距離燃料消耗量為；

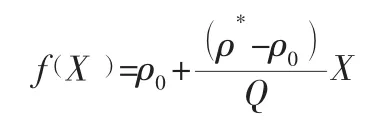
其中：ρ0、ρ*分別為空載、滿載下運輸單位距離時燃料的消耗量，X 為冷藏車的載重量，Q 為最大載重量。

由于發動設備只在運輸過程中啟動，所以發動設備產生的碳排放成本為：

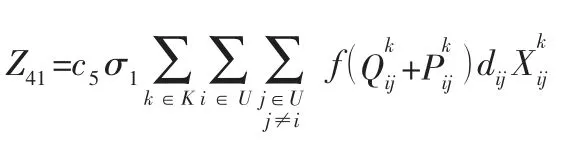
（2） 制冷設備產生的碳排放成本。由于冷藏車的制冷設備與發動設備是相互獨立的，所以等待過程中發動機熄火，而制冷設備仍繼續工作。冷藏車服務完最后一個顧客返回配送中心時，車上已沒有生鮮產品，因此會關閉制冷設備。所以制冷設備產生的碳排放成本為：

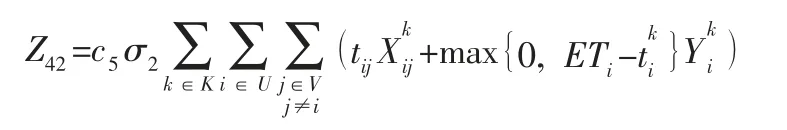
綜上，整個配送過程中的碳排放成本為：

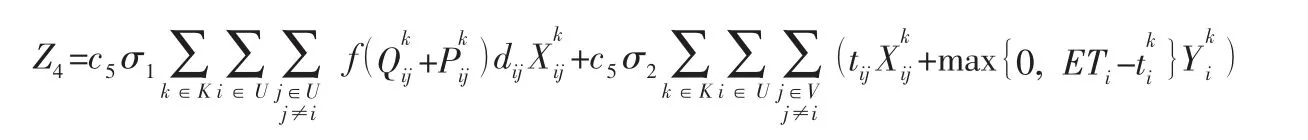
1.4.2 制冷成本

制冷成本主要包括運輸途中和等待過程中由于冷藏車內外溫差不同所引起的傳熱，以及裝卸過程中的熱空氣對流，可以通過制冷劑的消耗進行計算制冷成本。

（1） 運輸過程。運輸途中因為內外溫差單位時間產生的熱負荷為：

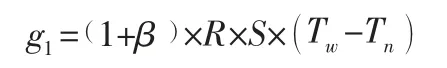
其中：β 表示車輛的折舊程度，R 為車輛的導熱率，S 為車輛平均受熱面積，可表示為分別表示車廂的內外表面積，Tn、Tw分別表示車廂的內外溫度。

所以，運輸途中的制冷成本為：

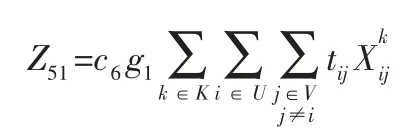
（2） 等待過程。由于等待過程中并未打開車門且制冷設備仍在工作，熱負荷產生函數不變，因此等待過程中的制冷成本為：

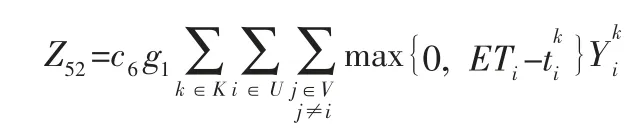
（3） 裝卸過程。冷藏車到達顧客進行裝卸服務時需打開車門，此時熱空氣對流，單位時間產生的熱負荷為：

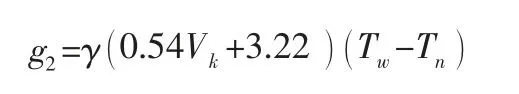
其中：Vk表示車廂的體積，γ 表示開門頻率系數。

所以，冷藏車在裝卸過程中的制冷成本為：

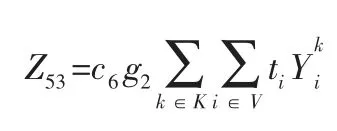
綜上，整個配送過程中的制冷成本為：

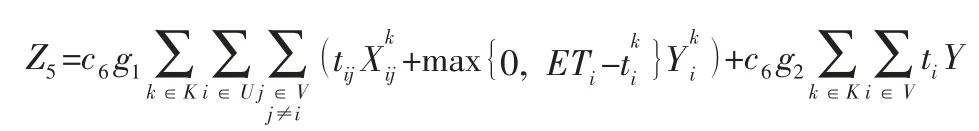
構建冷鏈VRPSPDTW 的數學模型如下：

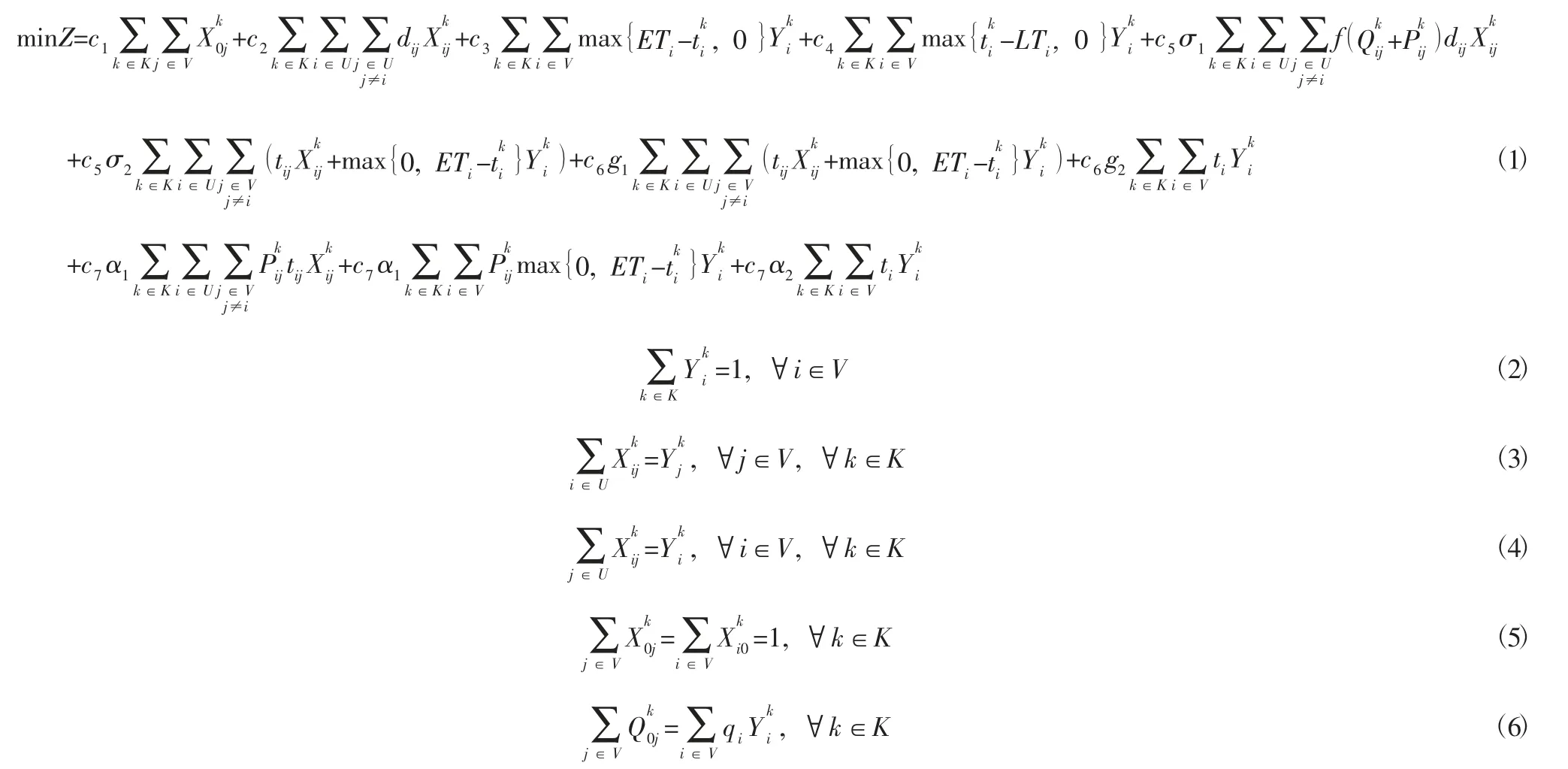
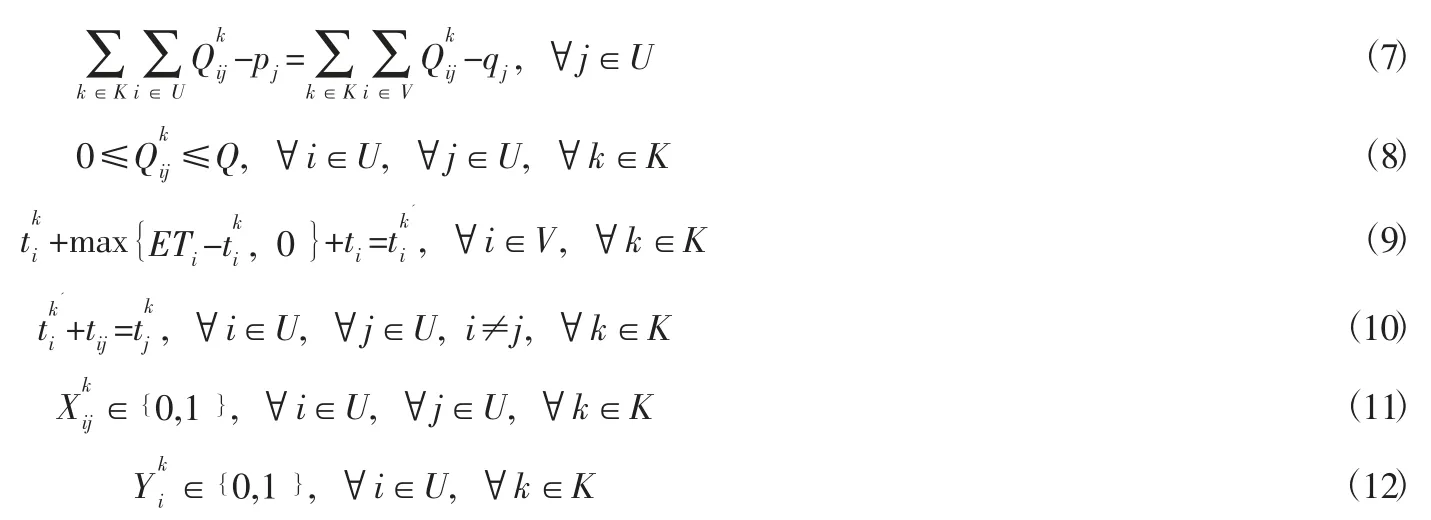
式（2） 保證每個客戶只能被一輛冷藏車服務，式（3） 和（4） 是兩個變量之間的關系，保證每輛冷藏車運輸時的載重量不能超過它的最大載重量，式（5） 保證每輛冷藏車從配送中心出發服務完所有客戶后必須回到配送中心，式（6） 保證冷藏車從配送中心出發時的載貨量等于線路上顧客的送貨總需求，式（7） 表示冷藏車經過顧客前后載重量變化，式（8） 保證冷藏車的載重量始終不超過最大容量，式（9） 和（10） 確保每輛冷藏車服務時間的連續性，式（11） 和（12） 表示兩個變量的取值范圍。

2 算法設計

TS 算法是一種逐步尋優的鄰域搜索算法，從初始解出發，記憶搜索過程中局部最優解，避免在下一次搜索過程中進行重復搜索，盡可能多地擴大搜索范圍，利用局部最優的信息逐步達到全局尋優。然而，標準TS 算法對初始解的依賴性很強，且很難對某一特定問題確定有效的禁忌長度，難以避免搜索過早收斂，從而陷入局部最優，錯失全局最優解。

本文設計改進的TS 算法采用RCRS 算法生成較優的初始解，保證解的質量，鄰域變換時應用了多鄰域隨機變換策略，實現對多個鄰域的快速搜索，有利于豐富鄰域解的多樣性，避免算法過早收斂，WTS 編碼方式縮短了鄰域運算時間，減少了迭代次數，響應性策略可以依據搜索進程動態地調整禁忌長度，加強了TS 算法的搜索機制，使得求解更加全局性。

下面介紹改進策略的具體流程。

2.1 路徑的編碼與解碼

VRP 問題的常見編碼方式是以配送中心節點（一般用0 表示） 作為子路徑的分隔符，如0-1-2-3-0-4-5-6-0 表示0-1-2-3-0 和0-4-5-6-0 兩條子路徑。一方面，這種方法需預先估計最小車輛數（需求總重量/車輛最大載重量），然而在有時間窗約束的前提下，車輛在進行服務時并不一定能滿載出發，易導致車輛的預估不足；另一方面，算法經過鄰域交換產生的新解不一定是可行解，需要進行檢驗，增大算法運行開銷。

基于此，本文選用的編碼方法為首先生成一條主路徑，然后將主路徑劃分為幾條子路徑，所以劃分算法的優劣對TS 算法的性能舉足輕重。Beasley[21]以車輛的載重量為劃分節點，若加上當前顧客的需求，子路徑的總需求大于車輛的容量，則以當前顧客為起點產生一條新的子路徑繼續進行劃分，直到主路徑劃分完畢。這種方法雖然效率很高，但對主路徑的顧客順序依賴性很強。李進等[22]繼承了Beasley 的劃分思想，提出了一種WSS（Weight and Speedbased Split） 劃分算法，但是對于VRPSPDTW 問題來說，這種方法沒有考慮時間窗以及顧客的取貨需求對路徑劃分的影響。因此本文對WSS 進行改進，提出適合VRPSPDTW 模型的WTS（Weight and Timebased Split） 算法，WTS 算法的具體步驟如下：

步驟1：初始化

假設節點i 的最小總費用（指車輛從配送中心出發，依次完成該節點及其前面所有節點的任務后返回配送中心這一過程中所發生的費用之和，包括固定成本和運輸成本） 為V［i ］，節點i 的最小總費用路徑的直接前繼節點（指上一輛車服務的最后一個客戶） 為P［i ］。

令V［i ］=∞，V［0 ］=0，P［i ］=i-1，?i∈V；

步驟2：最優路徑劃分

計算每個客戶節點i （i=1，2，…，n ）的最小總費用以及直接前繼節點，置i=1；

步驟2.1 令當前車輛的載重量load=0，總費用cost=0，令j=i；

步驟2.2 load=load+第j 個節點的需求量；

步驟2.3 若load＞Q 或不滿足時間窗，則i=i+1，轉步驟2.1；否則轉步驟2.4；

步驟2.4 若V ［j- 1 ］+cost＜V［j ］，則V［j ］=V ［j- 1 ］+cost，P［j ］=i-1；

步驟3 算法終止

所有顧客都被插入路徑中，若j＞n，則算法結束，否則令j=j+1，轉步驟2.2。

2.2 初始解的構造

標準TS 算法隨機生成初始解進行迭代搜索，這種生成方法雖然簡單有效，但是Tan 等[23]研究發現TS 算法對初始解有一定的依賴性，初始解的優劣將最終影響最優解的質量。為了保證初始解的質量，本文對Dethloff[24]解決VRPSPD 問題時提出的RCRS（Residual Capacity Radial Surcharge） 算法進行改進，加入時間窗約束，生成初始解。

RCRS 算法的具體步驟如下：

步驟1：選擇種子客戶

計算所有未路由的客戶的最早開始服務時間 （=max ｛車輛從配送中心到達顧客的時間，顧客允許的最早時間窗｝），選擇開始服務時間最小的客戶作為種子客戶。

步驟2：判斷是否有可插入位置

步驟2.1 種子客戶選好后，生成初始路徑（如0-1-0，該路徑有2 個插入位置）。判斷是否存在未路由客戶，若存在，繼續下述步驟，否則轉步驟4。

步驟2.2 依次判斷未路由客戶是否滿足插入位置的要求（載重量約束，時間窗約束），若存在可插入位置，轉步驟3，否則轉步驟1。

步驟3：計算可插入位置RCRS 標準值

計算可插入位置的RCRS 標準值，計算方法與文獻[24]相同，最后選擇RCRS 標準值最小的客戶插入，然后轉步驟2.2。

步驟4：算法終止

所有客戶都被插入路徑，算法終止。

2.3 鄰域結構設計

禁忌搜索基于鄰域變換進行搜索，確定鄰域操作至關重要。WTS 編碼方法使得鄰域操作時簡單方便，只需進行內部操作即可。本文選用3 種廣泛應用于車輛路徑問題的鄰域結構，操作時隨機選擇其中一種。例如解為123456，下劃線處為隨機選擇的兩個顧客i 和j，結果如下：

（1） 點交換。將顧客i 和j 的位置互換，得到：153426；

（2） 點插入。將顧客i 插入到j 后，得到：134526；

（3） 點逆序。將顧客i 和j 之間的顧客逆序，得到：124356。

2.4 禁忌對象及禁忌長度

將移動元素作為禁忌對象，對三種鄰域操作，建立三個禁忌表來存儲相應的禁忌對象。禁忌長度的確定是TS 算法的關鍵，決定了禁忌時間的長短，從而影響解的搜索范圍和質量，禁忌長度過短則易陷入循環，算法難以跳出局部最優點；過長則會加大數據存儲量，甚至導致算法無法繼續進行。標準TS 選用固定的禁忌長度，然而對于不同的問題很難確定統一的禁忌長度。響應性禁忌搜索算法（Reactive Tabu Search，RTS） 對標準禁忌搜索算法進行改進，基于解的重復次數和解的重復時間差在搜索過程中動態調整禁忌長度。調整規則有兩種方式，一是解重復出現的間隔在設定的最大間隔之內，表明禁忌長度過短，增大禁忌長度；二是當前時間距離上次禁忌長度發生改變的時間超過預設值，表明搜索區域過大，減小禁忌長度。若解的重復次數超過預設值，表明解陷入混沌，即陷入局部最優，此時算法采用逃離機制，跳出當前區域，重新進行搜索。為了避免禁忌過度，每當歷史最優解被更新，清空禁忌表，使搜索更自由。RTS 算法具體步驟如下：

步驟1：初始化RTS 相關參數

步驟2：RTS 算法框架

步驟2.1：生成候選解，找出當前最優解；

步驟2.2：把當前最優解存入Hash 表，判斷是否重復，若重復，轉步驟2.3，反之轉步驟2.5；

步驟2.3：解重復次數chaotic=chaotic+1，若chaotic＞混沌標志數chaos，轉步驟3，反之轉2.4；

步驟2.4：判斷重復間隔R 是否超過預設值Rave，若R＜Rave，禁忌長度，L=1.1*L，Rave=0.1*R+0.9*Rave，反之轉步驟4；

步驟2.5：判斷當前時間距離上次禁忌長度發生改變的時間tT 是否超過預設值GapMax，若tT＞GapMax，L=0.9*L，轉步驟4，反之轉步驟4。

步驟3：逃離機制

跳出當前搜索區域，重新生成初始解進行搜索。

步驟4：算法終止

達到預先設定最大迭代步數，算法終止。

2.5 ITS 算法流程

下面給出ITS 算法的具體流程。

步驟1 初始化

輸入各改進策略的算法參數；設置算法終止條件：迭代代數達到最大迭代數Nmax或者達到允許最優解未改進的最大次數Emax；設迭代計數器t=0，最好解未改進次數t1=0；采用改進RCRS 算法生成初始解S，并把該解置為Sbest和Snow，計算初始解的適應度值F（S ）；當前候選解數目n=0，最大候選解數目為nmax，候選集為C。

步驟2 生成候選解

從三種鄰域變換中隨機選取一種作用于當前解Snow生成候選解S'，將S'置入候選集C 中，n=n+1；若n＞nmax，轉步驟3，反之轉步驟2。

步驟3 候選解排序

采用WTS 算法對C 集合中的候選解進行解碼計算，選出當前最優解S*，記錄其適應度值F （S*）。

步驟4 調整禁忌長度

將F （S*）代入RTS 算法，動態調整禁忌長度L。

步驟5 更新統計信息

若F （S*）＞=F （Sbest），則t1=t1+1；否則Sbest=S*，t1=0，Snow=S*。

步驟6 更新禁忌表

將當前解S*的禁忌對象放入禁忌表中。

步驟7 算法終止

若t＞Nmax或t1＞Emax，算法終止輸出最優解Sbest，否則轉步驟2。

3 算例實驗與分析

3.1 測試環境與測試數據

實驗環境如下：Intel（R） Core（TM） i7-8550U CPU，8GB RAM，操作系統為Window 10，編程環境為C#。

Wang 等[14]提出的測試算例已成為求解VRPSPDTW 問題的國際通用算例，本文亦選取該算例進行實驗。為避免偶然性，每個算例獨立運行20 次，取其中的最優值作為實驗結果。

3.2 實驗一

為驗證改進策略對TS 算法性能的提升，選取9 個小規模算例進行實驗，將結果與標準TS 算法進行比較。實驗對比結果如表1 所示，其中，NV（Number of Vehicle） 表示所需要的車輛數；TD（Travel Distance） 表示總運輸距離；Gap 表示2 個算法的差距，其中TD%= （改進TS-標準TS ）/改進TS。觀察發現，9 組測試算例中，改進TS 在NV 目標值上有2 組優于標準TS，而對于TD 目標值，改進效果明顯，共有6 組有較大改進，最大改進率為3.06%。

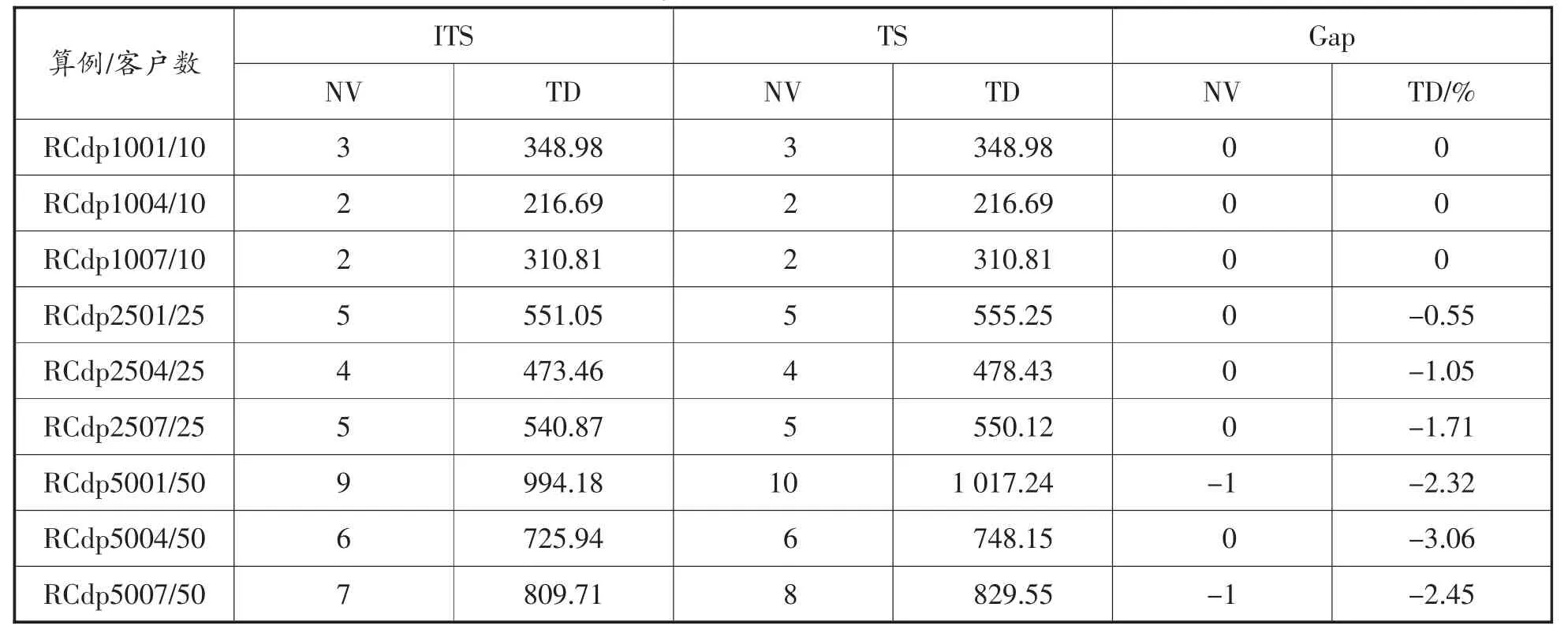
表1 小規模客戶改進TS 與標準TS 實驗結果對比

為了進一步研究ITS 和TS 的算法的收斂性能，選取RCdp5001 算例，其最優結果的迭代過程如圖1 所示，x 軸表示算法迭代次數，y 軸表示目標函數TD 值。由圖1 中可以看出，RCRS 算法保證ITS 算法比TS 算法隨機生成的初始解更優，更有利于接下來的搜索，RTS 算法動態調整禁忌長度，提高跳出局部最優的可能性，ITS 算法可以更快的跳出局部最優。

3.3 實驗二

為進一步測試ITS 算法的有效性，選取9 個小規模算例和10 個大規模算例進行實驗，將實驗結果與Wang 等[14]設計的遺傳算法（Genetic Algorithm，GA）、Wang 等[16]設計的并行模擬退火算法（parallel-Simulated Annealing，p-SA）、王超等[17]設計的離散布谷鳥算法（Discrete Cuckoo Search，DCS） 取得的最優實驗結果進行比較，對比結果如表2 所示。

觀察結果得出，9 組小規模算例中，1 組算例更新了最優解，7 組算例達到最優解，1 組算例略差于最優解。對于10 組大規模算例，4 組算例更新了最優解，最大改進率為8.40%，2 組算例達到最優解，1 組算例NV 多1 輛，但TD 改進0.51%，剩余3 組算例結果略差于最優解。通過實驗可以看出，改進禁忌搜索算法加入RCRS 算法和RTS 算法后，能更有效地跳出局部最優進行搜索，加快尋優速度，驗證了改進策略的有效性。

4 結束語

本文研究了帶時間窗的同時取送貨車輛路徑問題，以車輛的固定成本、運輸成本、車輛超時的時間窗成本、貨物的貨損成本、保鮮的制冷成本以及考慮環保的碳排放成本之和為目標構建了配送模型。基于標準TS 的框架，采用RCRS 插入算法生成初始解，進行鄰域搜索時，應用WTS 算法進行路徑劃分，減少了可行解的驗證時間，RTS 算法動態調整禁忌長度，提高搜索的效率，通過與標準算例的對比，結果表明ITS 算法在求解該問題上能得到可接受的可行解。

本文沒有考慮車輛行駛速度帶來的影響，后續研究中將考慮速度隨時間而變化，即解決時間依賴性帶時間窗的同時取送貨問題（TDVRPSPDTW），對速度可變情況下車輛調度進行規劃，來尋得最優調度。

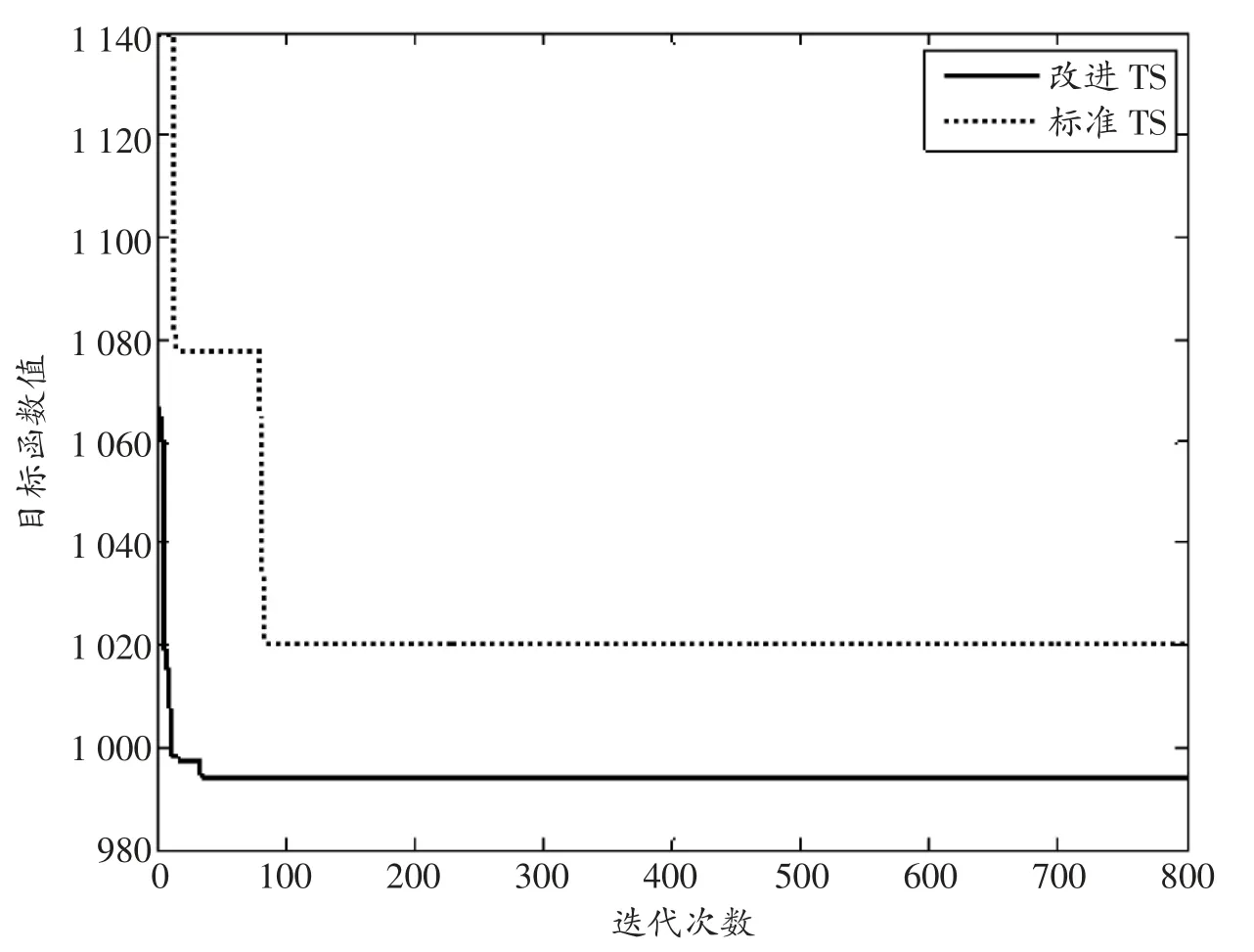
圖1 改進TS 與標準TS 進化過程比較

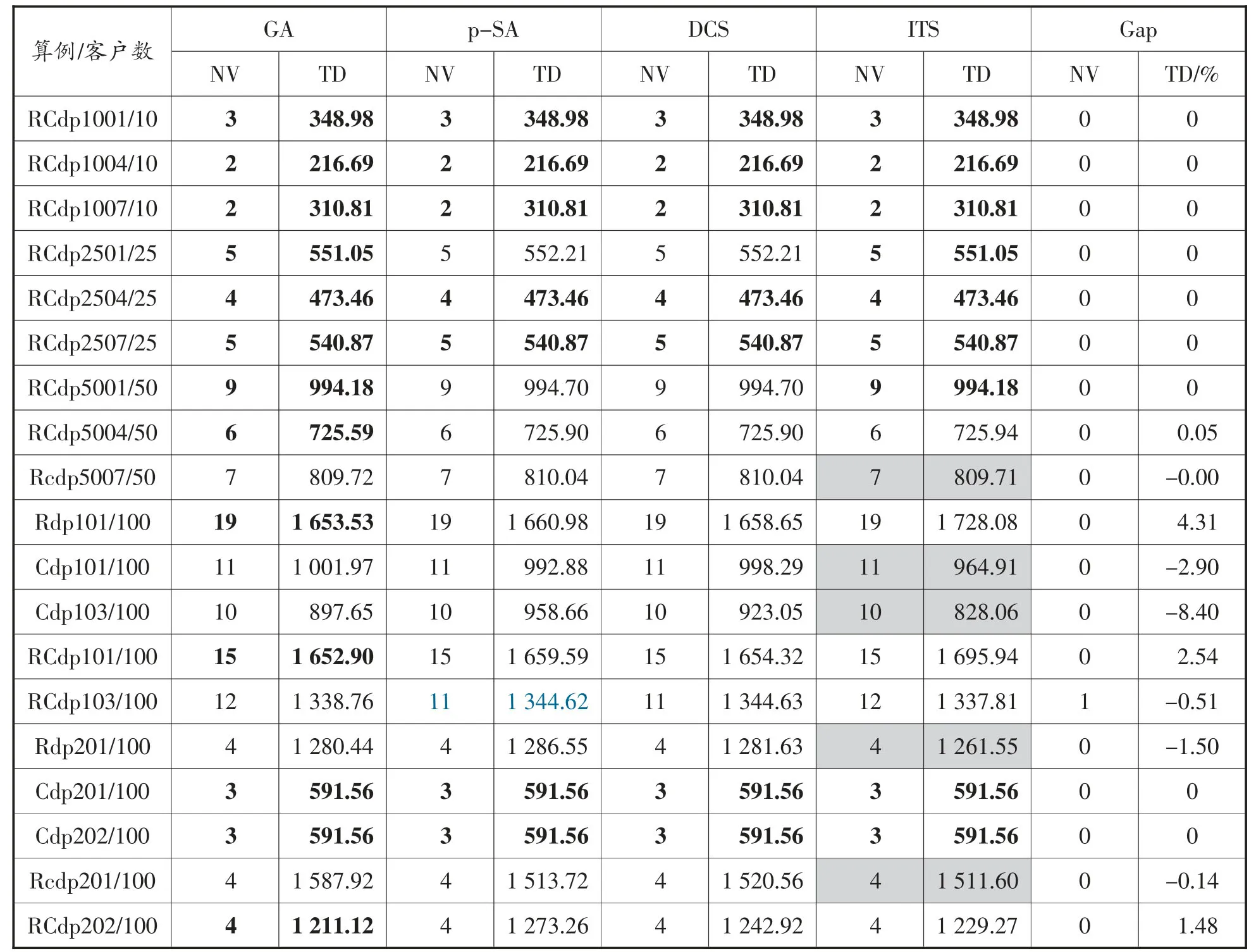
表2 比較GA、p-SA、DCS 和ITS 算法的結果