新型液壓式動力反共振隔振器的試驗研究

鄧雨河，龍新華

(上海交通大學 機械與動力工程學院，上海 200240)

0 引言

隨著隔振技術在工業領域的廣泛應用，低頻線譜隔振問題已成為日益突出的研究熱點和難點[1]。傳統被動隔振系統能夠較好地隔離中、高頻振動，但低頻隔振能力較差[2]。為了擴大隔振范圍，需要減小系統剛度來獲得低頻隔振能力，但往往存在著系統穩定性和隔振效果的權衡問題[3]。利用慣性耦合的動力反共振技術針對特定頻率的激勵產生的慣性力與彈簧作用力相位相反，從而實現線譜振動的隔離[4]。FLANNELLY W.G[5]提出了一種機械式動力反共振器(DAVI)，解決了直升機主減系統隔振頻率低和靜位移不能太大的矛盾[6]。HALWES.D.R等人[7-8]提出了一種液彈式動力反共振隔振器(LIVI)，利用慣性液體在流動過程中產生的動壓力和彈性力相互抵消，從而實現隔振效果，其采用流體作為慣性質量，結構更加緊湊。為拓寬隔振器的反共振隔振頻帶，N. F. Du Plooy[9]提出剛度可調的帶空氣彈簧的液壓隔振器。

本文基于動力反共振隔振原理設計制作了一種新型液壓式動力反共振隔振器，進行了一系列試驗研究，驗證反共振隔振原理的正確性。基于試驗結果對原有的反共振隔振模型進行修正，進一步驗證了隔振模型的合理性。為了調節隔振器的反共振頻率，進行了在不同慣性質量、初始靜壓下的試驗測試，基于試驗結果提出兼顧反共振頻率可調性與隔振效果的方法。

1 試驗裝置

液壓式動力反共振隔振器由內筒、外筒、波紋管、慣性質量等部件組成，結構示意圖見圖1。其內筒和外筒通過橡膠硫化成一體，橡膠提供隔振器剛度且作為隔振器的密封件，隔振器封閉腔室內充滿水等低黏性液體。隔振器基座與振源(液壓振動臺)剛性連接，負載(被隔振對象)與隔振器上端蓋剛性連接，振源激振力由基座傳至負載。

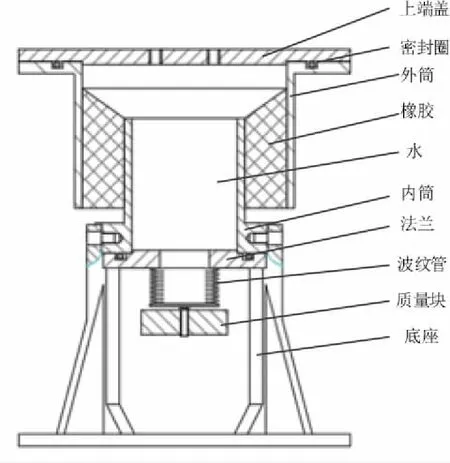
圖1 液壓隔振器結構

圖2是隔振器試驗裝置，液壓隔振器的試驗特性與隔振器封閉腔室的液體初始靜壓有關[10]，隔振器的進水泵口2與加壓裝置連接，通過調節加壓裝置進而改變初始靜壓。負載和慣性質量塊僅在軸向上運動，兩組傳感器分別裝在隔振器上端蓋和內筒上。

1—上端蓋1#傳感器；2—進水泵口；3—液壓傳感器；4—上端蓋2#傳感器；5—內筒傳感器。圖2 液壓隔振器試驗裝置

2 數學模型

液壓隔振器包括固體、液體兩種形式的材料，可以簡化為機械DAVI隔振器力學模型。圖3是液壓隔振器的物理模型及其等效模型，其上液腔與波紋管通道面積之比等效于機械式DAVI隔振器中的杠杠比。隔振器外筒和被隔振對象連接，內筒和基礎激勵連接。被隔振對象質量為m1，內筒質量為m2，慣性質量塊質量為m3，其位移分別為x1、x2、x3；外筒內直徑、內筒外直徑、波紋管直徑分別為db、d0、da，其對應的截面積分別為Ab、A0、Aa；橡膠動剛度、波紋管剛度分別為k、k1，作用在內筒上的激勵力為f。

圖3 液壓隔振器物理模型及其等效模型

隔振器在受到外界激勵時，隔振器的內筒、外筒、慣性質量塊之間會產生相對運動，由流體連續性可知，運動前后上液腔減少的液體體積V1等于波紋管下液腔增加的液體體積V2，其中:

(1)

V2=Aa(x2-x3)

(2)

由V1=V2，得

x3=αx1+(1-α)x2

(3)

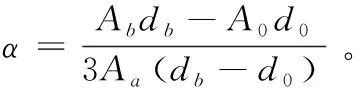
系統動能

(4)

系統勢能

(5)

不考慮阻尼，由拉格朗日方程得到系統動力學方程有：

(6)

設外激勵x2=X2ejωt，x2=X2ejωt，由上式可以得到隔振器的位移傳遞率

(7)

由式(7)可以得到

系統的共振頻率

(8)

反共振頻率

(9)

由式(9)可以看出，隔振器的反共振頻率與隔振器橡膠動剛度、波紋管剛度、慣性質量及隔振器放大比有關，因此可以選擇合適的隔振器參數，從而得到特定的反共振頻率。

3 試驗及理論對比分析

3.1 隔振器參數辨識

為了驗證液壓隔振器動力反共振理論，設計和加工了圖1所示的液壓隔振器，其具體尺寸為：da=25mm，db=136mm，d0=80mm，k1=20.59N/mm。通過隔振器無水情況下的振動試驗可以擬合得到隔振器相關參數，圖4是負載為13kg的頻響曲線，表1是在不同負載質量下試驗得到的隔振器固有頻率。

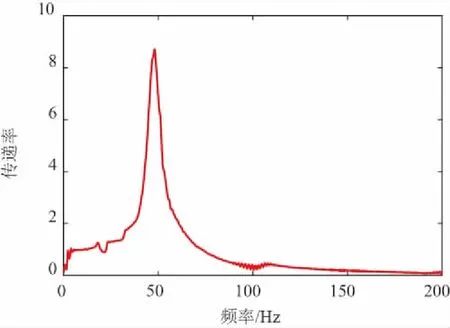
圖4 無水情況下的振動傳遞實驗曲線

表1 無水情況和不同負載下隔振器固有頻率

得到以上隔振器參數后，進行隔振器有水情況下的振動測試，初步驗證動力反共振理論。圖5是在慣性質量為0.3kg、負載質量23kg下的振動測試試驗結果，可以看出隔振器在42.2Hz的頻率下具有較好的隔振效果。

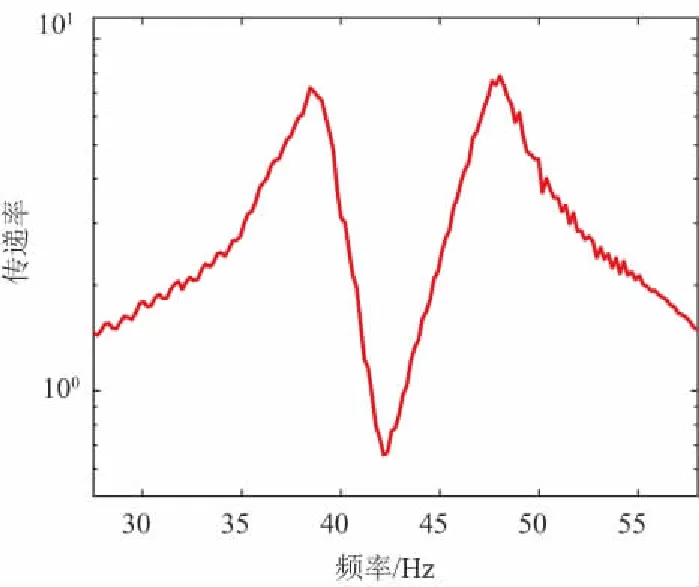
圖5 有水情況下的振動傳遞實驗曲線

由式(8)和式(9)可以得到隔振器的理論共振頻率38.2Hz和反共振頻率43Hz，與圖5中試驗共振頻率38.5Hz及反共振頻率42.2Hz基本一致，但是試驗結果中的二階共振峰是式(7)中未出現的，為了對試驗結果進行進一步理論分析，下面建立兩自由度隔振系統對原隔振模型進行修正。

3.2 隔振器模型修正

參考文獻[8]對液壓式動力反共振隔振器建立的考慮隔振器體積剛度的機械式集中參數隔振器模型，在圖3所示的機械杠桿式DAVI等效模型中考慮鉸支點處的非完全剛性，對應鉸支點處的位移為x4，其鉸支點剛度對應液壓隔振器中波紋管徑向膨脹帶來的隔振器體積剛度，其等效數學模型見圖6。

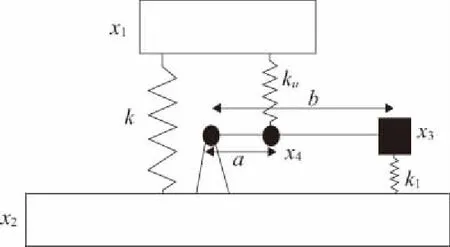
圖6 考慮隔振器體積剛度的等效數學模型

系統動能

(10)

系統勢能

(11)

不考慮阻尼，由拉格朗日方程得到系統動力學方程式有：

(12)

設外激勵x2=X2ejωt，x1=X1ejωt，由上式可以得到隔振器的位移傳遞率

(13)

進一步得到隔振器的反共振頻率

(14)

令式(13)分母為0，可以得到隔振器的第一階固有頻率fp1和第二階固有頻率fp2。

由于隔振器的體積剛度ku未知，為了對以上隔振器動力學模型進行驗證，采用參數識別法，將不同慣性質量m3下的反共振頻率fz代入式(14)中，進而識別出未知參數即隔振器的體積剛度ku，進一步將參數代入共振頻率fp1和fp2中，從而驗證改進后的動力學模型的合理性。圖7、圖8是隔振器在慣性質量分別為0.3kg、0.6kg負載質量下的振動傳遞試驗曲線。

由圖7、圖8可以看出0.3kg、0.6kg的慣性質量對應的反共振頻率分別為42.1Hz、33.3Hz，將其代入式(14)中，可以擬合得到ku=123.39N/mm。進一步，可以求得fp1和fp2，其結果見表2、表3。

圖7 0.3kg慣性質量不同負載的振動傳遞試驗曲線

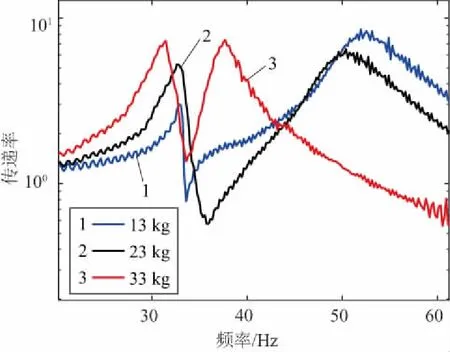
圖8 0.6kg慣性質量不同負載的振動傳遞試驗曲線

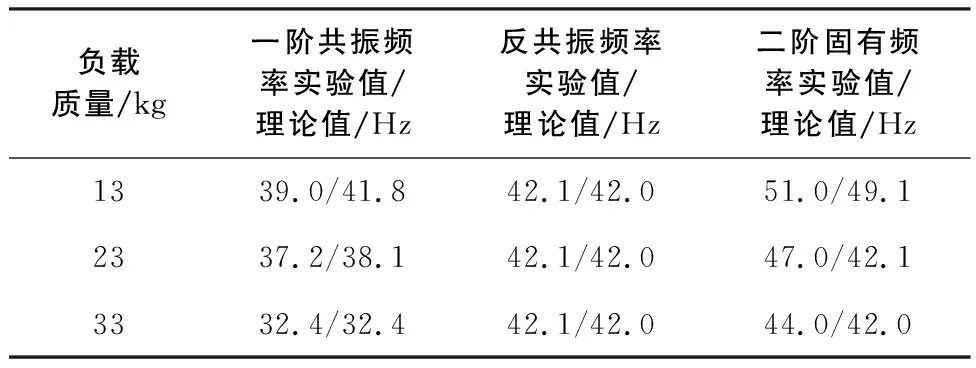
表2 0.3kg慣性質量不同負載下理論共振頻率和反>共振頻率與試驗值對比

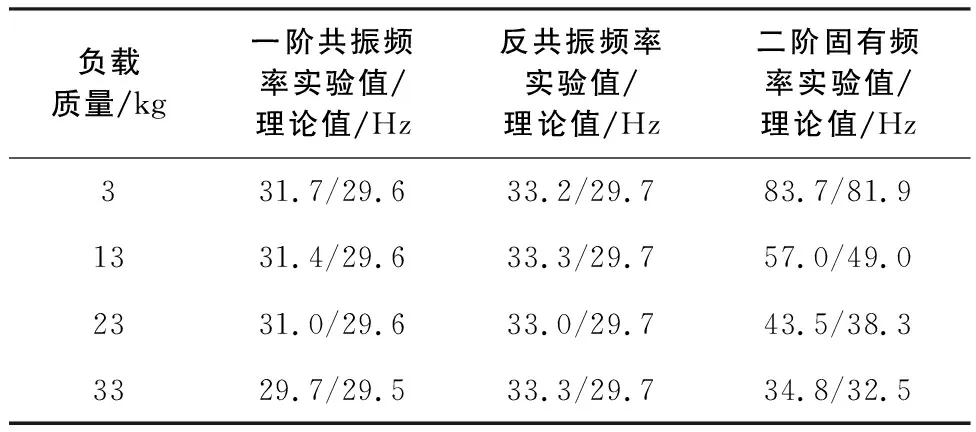
表3 0.6kg慣性質量不同負載下理論共振頻率和反共振頻率與試驗值對比

由表2、表3可以看出，隔振器的共振頻率及反共振頻率理論值與試驗結果基本一致，說明修正后的隔振器模型能夠較好地預測試驗結果。

3.3 初始靜壓影響性分析

文獻[10]指出液壓隔振器的隔振特性與液體初始靜壓有關，為了探究其關系，在不同液壓下進行新型液壓隔振器的振動傳遞試驗：在慣性質量為0.9kg，在13kg、23kg、33kg不同質量的負載下，分別在隔振器初始液壓為0.1MPa、0.2MPa、0.3MPa、0.4MPa的不同工況下進行振動傳遞試驗，實驗結果如圖9-圖11所示。

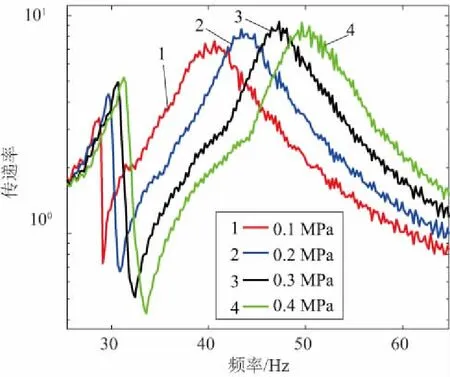
圖9 負載13kg不同初始液壓下的頻響曲線

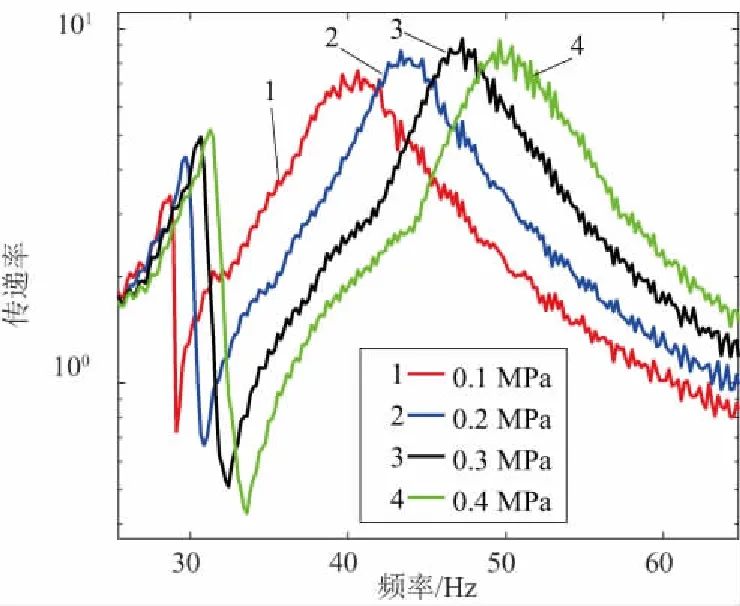
圖10 負載23kg不同初始液壓下的頻響曲線

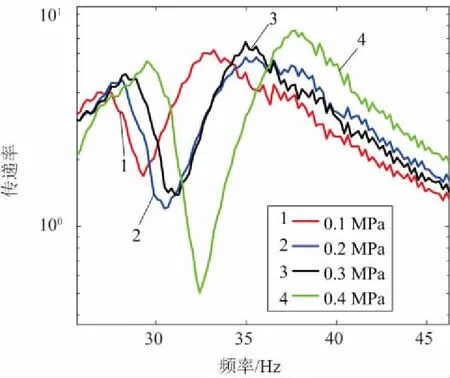
圖11 負載33kg不同初始液壓下的頻響曲線

由以上試驗結果可以看出，在慣性質量不變的情況下，增大隔振器液體的初始液壓，隔振器的反共振頻率點向右下側移動，說明增大初始液壓可以增大隔振器的反共振頻率，并且可以進一步提高隔振效率。由修正后的液壓隔振器模型可以知道，隔振器的共振頻率和反共振頻率與隔振器的體積剛度有關，隔振器的體積剛度會隨著隔振器液體的初始靜壓增大而增大，從而影響隔振性能。

4 結語

本文設計制作了一種新型液壓式動力反共振隔振器，進行了大量試驗研究，并與理論分析進行比較，得到如下結論：

1) 考慮隔振器體積剛度的新型液壓隔振器模型能夠較好地預測隔振器試驗結果，較單自由度集中參數模型能夠更好地預測系統的二階共振峰值。

2) 新型液壓隔振器的反共振頻率可通過調節慣性質量的大小來實現，隔振系統的兩階共振峰值都會隨著負載的增大而減小，但對反共振頻率沒有影響。

3) 隔振器的初始液壓影響著隔振效果，合理增加初始液壓能夠提高隔振效率。