基于頻響函數識別結構非線性模態參數的方法

單衛東，臧朝平，張根輩，王平，鄒亞晨，倪徳

(1.南京航空航天大學 能源與動力學院，江蘇 南京 210016； 2.中國航發動力機械研究所，湖南 株洲 412002)

0 引言

模態分析理論和參數識別方法是模態參數識別的重要組成部分。由于準確、可靠地識別出結構的非線性模態參數難度較大，當前的模態分析和參數識別方法主要基于線性模型[1-2]，對于系統中的非線性常常忽略或者作為不確定性來處理。然而大多數的非線性結構并不能完全忽略其中的非線性，當作不確定性來處理也會帶來很多誤差。因此，建立一個準確、可靠的非線性模態參數識別方法是十分重要的。

非線性模態測試方法(nonlinear modal testing，NLMT)的研究在近年來取得了一定進展。臧朝平等[3-4]提出了分別用恒定位移幅值下的正弦激勵識別非線性剛度參數和恒定速度幅值下的正弦激勵來識別非線性阻尼參數的方法。CARRELLA等[5]提出了從測量的頻響函數識別和量化工程結構中非線性的復頻響函數法。

本文在文獻[3-5]的基礎上，提出在任意給定的速度響應幅值處，阻尼為常數，即將阻尼比描述成與速度幅值相關的參數，并引入加速度頻響、速度頻響、位移頻響函數之間的轉化關系，利用位移頻響函數識別出與位移幅值相關的固有頻率，利用速度頻響函數識別出與速度幅值相關的阻尼比。通過非線性系統的仿真測試，驗證該方法既能夠檢測出系統的剛度非線性，也能檢測出阻尼非線性，且識別的非線性模態參數足夠精確。

1 結構非線性模態參數辨識方法

1.1 非線性模態參數的線性等效

對于單自由度非線性系統，在受到簡諧力的作用時，運動微分方程為：

(1)

通過步進正弦掃頻信號激勵后，可以將系統的位移頻響函數定義為：

(2)

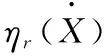
1.2 非線性模態固有頻率識別

在任意給定的位移響應幅值處，存在一對點來定義相同的位移頻響函數，如圖1所示。如果不能直接測量得到位移幅值，可以通過位移頻響函數乘以力來得到響應 ，即X(ω)=Hd×F。

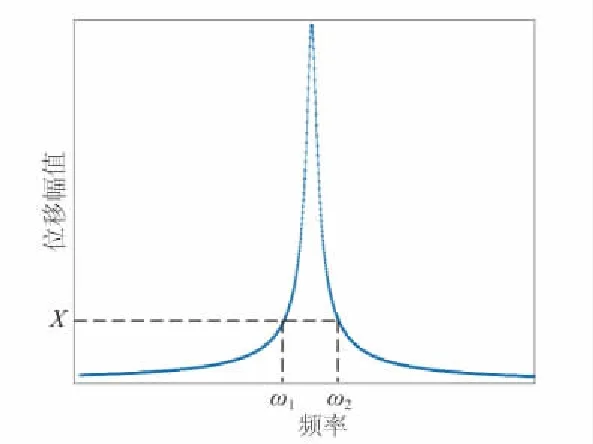
圖1 位移幅值線性化

在每個給定位移響應幅值下，可以通過一對對稱的位移FRF點來定義位移頻響函數的實部和虛部。

(3)

由式(3)可以得到與位移響應幅值相關的固有頻率：

(4)

通過截取位移響應峰值兩端對稱的位移頻響函數點，可以建立起固有頻率與位移幅值、激勵力幅值之間的對應關系：

ωr=f(X,F)

(5)

1.3 非線性模態阻尼比識別

圖2 速度幅值線性化

在每個給定速度響應幅值下，可以通過一對對稱的速度FRF點來定義速度頻響函數的實部和虛部。

(6)

由式(6)可以得到與速度幅值相關的模態損失因子：

(7)

其中模態損失因子是模態阻尼比2倍的關系ηr≈2ξ。

通過截取速度幅值兩端對稱的速度頻響函數點，即可以建立起阻尼比與速度幅值、激勵力幅值之間的對應關系：

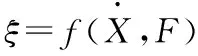
(8)

2 非線性模態分析方法的仿真測試

2.1 非線性與線性系統的仿真驗證

將上述方法分別應用于線性和非線性系統(同時包含剛度非線性項和阻尼非線性項)，對系統進行仿真分析來驗證該方法的有效性。這里選用一個同時帶立方剛度和平方阻尼的非線性單自由度系統，來與線性系統(其中knl=0，cnl=0)進行對比，其他仿真取值都一樣,非線性系統的表達式如下：

(9)

在激勵力幅值為0.2N、0.4N、1N時，線性系統與非線性系統的位移響應如圖 3和圖4所示。隨著激勵力幅值的增大，線性系統的位移響應峰值對應的頻率不發生變化，而非線性系統的位移響應峰值對應的頻率發生了明顯的變化，即所謂的“頻移”現象，這是非線性的表現。

圖3 線性系統位移響應

圖4 非線性系統位移響應

對線性系統和非線性系統的位移頻響函數進行分析，可以識別出非線性模態參數：與位移幅值相關的固有頻率。如圖5和圖6所示，隨著激勵力幅值的增大，位移幅值逐漸增大，線性系統的固有頻率隨著位移幅值的增大保持不變，而非線性系統的固有頻率隨著位移幅值增大而增大。固有頻率的變化反映出非線性系統包含的非線性剛度因素。

圖5 線性系統固有頻率隨位移幅值的變化

圖6 非線性系統固有頻率隨位移幅值變化

對線性系統和非線性系統的速度頻響函數進行分析，可以識別出非線性模態參數與速度幅值相關的阻尼比。如圖7和圖8所示，隨著激勵力幅值的增大，速度幅值逐漸增大，線性系統的阻尼比隨著速度幅值的增大保持不變，而非線性系統的阻尼比隨速度幅值的增大而增大。阻尼比的變化反映出非線性系統中包含的非線性阻尼因素。

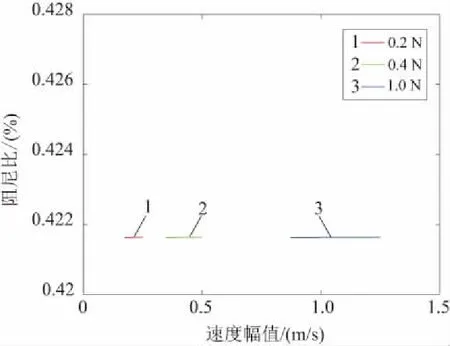
圖7 線性系統阻尼比隨速度幅值的變化

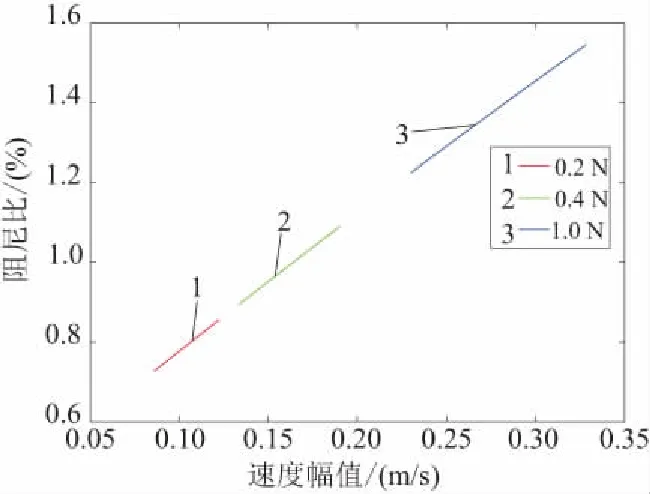
圖8 非線性系統阻尼比隨速度幅值的變化

2.2 非線性剛度函數的提取

將諧波平衡法應用到運動方程

(10)

求得等效剛度的表達式：

(11)

式中X是響應的幅值。通過式(3)可以發現等效剛度是從一個恒定值(底層線性系統)開始，與位移幅值2次方的關系開始增加。通過上面非線性模態識別方法，基于仿真分析得到位移頻響函數，可以提取得到系統固有頻率隨位移幅值的變化，求得非線性等效剛度的表達式：

(12)

如圖9所示，在激勵幅值為1N時，通過非線性模態參數識別方法(CFRF)提取的等效剛度函數與諧波平衡法(HBM)的對比，誤差不超過0.5%。因此，本方法能精確地識別出非線性系統的剛度函數。

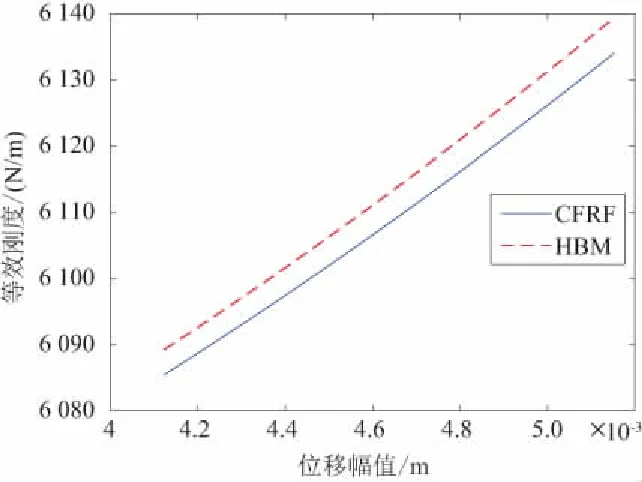
圖9 仿真提取剛度函數與諧波平衡法的對比

2.3 非線性阻尼函數的提取

類似地，將諧波平衡法應用到運動方程：

(13)

求得等效阻尼的表達式：

(14)

穩態速度響應的幅值近似為：

V=ωX

(15)

則有：

(16)

通過上式可以發現等效阻尼與速度幅值呈線性的關系。通過上面非線性模態識別方法，基于仿真分析得到速度頻響函數，可以提取得到系統阻尼比隨速度幅值的變化，求得非線性等效阻尼的表達式：

(17)

如圖10所示，在激勵幅值為1N時，通過CFRF提取的等效阻尼函數與HBM的對比，誤差不超過1%。因此，本方法能準確地識別出非線性系統的阻尼函數。

圖10 仿真提取阻尼函數與諧波平衡法的對比

3 結語

本文提出了基于頻響函數識別結構非線性模態參數的方法。主要得到以下結論：

1) 基于等效線性化理論，通過標準的模態試驗，可以識別和量化系統的非線性模態參數，具有重要的工程實用價值。

2) 通過非線性系統與線性系統的仿真對比，驗證該方法既可以檢測系統的剛度非線性，也可檢測阻尼非線性。

3) 通過非線性模態參數提取的非線性等效剛度和阻尼函數，與諧波平衡法的結果誤差均在1%以內，驗證了該方法識別非線性模態參數的精確性。