基于PCE法的某渦輪泵轉(zhuǎn)子動力學(xué)特性不確定性分析

沙粒子，王曉偉，穆鵬剛

(1. 南京航空航天大學(xué) 能源與動力學(xué)院，江蘇 南京 210016； 2. 液體火箭發(fā)動機(jī)技術(shù)國防科技重點(diǎn)實(shí)驗(yàn)室，陜西 西安 710100)

0 引言

渦輪泵是火箭發(fā)動機(jī)的心臟，轉(zhuǎn)子系統(tǒng)是渦輪泵的重要核心部件，其運(yùn)行的穩(wěn)定性及可靠性直接關(guān)系到渦輪泵的壽命。轉(zhuǎn)子是旋轉(zhuǎn)機(jī)械振動的主要來源，如何減少轉(zhuǎn)子振動是設(shè)計制造旋轉(zhuǎn)機(jī)械的重要課題[1]。

研究轉(zhuǎn)子的動力學(xué)問題，首先需要對轉(zhuǎn)子進(jìn)行有限元建模。有限元建模需要足夠的精度保證建立模型的準(zhǔn)確性。除了確保模型的精度以外，還需要考慮計算效率。如果一個模型占用的空間過大，將會嚴(yán)重降低其計算效率。因此，平衡精度與效率問題就成了有限元建模的難點(diǎn)所在。蔡力鋼等[2]研究了多種約束的機(jī)械式主軸有限元建模，發(fā)現(xiàn)把主軸考慮為用梁單元結(jié)果更為精確。邊杰等[3]研究了當(dāng)一種發(fā)動機(jī)轉(zhuǎn)子沒有具體樣機(jī)時可用超模型去替代實(shí)物模型的有限元建模方法。

因?yàn)檗D(zhuǎn)子本身的構(gòu)造復(fù)雜多變，加工難度高，會產(chǎn)生一系列不確定性的因素，如材料屬性、加工尺寸、測量誤差等。對于轉(zhuǎn)子這樣的高精尖部件來說，很小的誤差可能會產(chǎn)生巨大的影響。因此研究轉(zhuǎn)子的不確定性問題是很有必要的。白長青等[4]將不確定因素表示為一維隨機(jī)場函數(shù)，給出了轉(zhuǎn)子系統(tǒng)的隨機(jī)響應(yīng)分析方法。不確定性問題的研究方法有很多，其中多項(xiàng)式混沌展開法(polynomial chaos expansion, PCE)憑借其堅(jiān)實(shí)的數(shù)學(xué)基礎(chǔ)和良好的性能，近年來受到越來越多的關(guān)注，在數(shù)學(xué)及工業(yè)領(lǐng)域的應(yīng)用也越來越廣泛。本文將此方法應(yīng)用到所建立好的轉(zhuǎn)子模型上，驗(yàn)證了此方法的有效性，并指出不確定性對轉(zhuǎn)子系統(tǒng)產(chǎn)生的重要影響。

1 基于PCE的轉(zhuǎn)子動力學(xué)建模理論

多項(xiàng)式混沌理論總的來說就是用一系列與輸入?yún)?shù)分布類型對應(yīng)的正交多項(xiàng)式之和來近似精確地表示一個隨機(jī)擴(kuò)展的過程。最開始的多項(xiàng)式混沌是由WIENER[5-6]提出的，如式(1)所示。它是利用Hermite多項(xiàng)式來構(gòu)建模型的。

(1)

式中：α(α0,αi1,…)是需要求解的多項(xiàng)式系數(shù)；ξ(ξi1,ξi2,…)是服從標(biāo)準(zhǔn)正態(tài)分布的隨機(jī)變量。ξ=[ξi1,ξi2,…]的維數(shù)通常與原任意正態(tài)空間下的隨機(jī)輸入變量X=[X1,X2,…]的維數(shù)保持一致并存在一一對應(yīng)關(guān)系。Hn(ξi1,…,ξin)是階數(shù)為n的Hermite正交多項(xiàng)式。

對于轉(zhuǎn)子系統(tǒng)，主要由轉(zhuǎn)軸、作用在上面的圓盤和支承系統(tǒng)組成。根據(jù)M. I. Friswell等人[7]所著內(nèi)容，其中轉(zhuǎn)軸可以看成由不同分段的鐵摩辛柯梁單元組成，每個節(jié)點(diǎn)有4個自由度。對于有直徑變化、集中質(zhì)量、連接方式改變等情況，則需要在該處進(jìn)行分段。

將轉(zhuǎn)軸、盤、支承等全部結(jié)合起來組成整體轉(zhuǎn)子系統(tǒng)的動力學(xué)方程。其形式如下：

(2)

其中：M、G分別代表轉(zhuǎn)軸和盤的質(zhì)量矩陣、陀螺矩陣；K、C分別代表轉(zhuǎn)軸的剛度矩陣和阻尼矩陣；Kb代表支承的剛度矩陣；q是整個轉(zhuǎn)子系統(tǒng)上受到的激勵項(xiàng)。

將方程轉(zhuǎn)換到頻域系統(tǒng)，得到下式：

Z(ω)X(ω)=Q(ω)

(3)

其中：

Z(ω)=-ω2M+iω(C+ωG)+K+Kb

(4)

轉(zhuǎn)子動力學(xué)方程與其他系統(tǒng)動力學(xué)方程最大的區(qū)別就是它多了陀螺力項(xiàng)，因此會使系統(tǒng)的振動形式復(fù)雜更甚。接下來針對具體的轉(zhuǎn)子系統(tǒng)進(jìn)行不確定性建模分析。

2 某渦輪泵轉(zhuǎn)子模型

轉(zhuǎn)子的幾何構(gòu)造如圖1所示，由轉(zhuǎn)軸、誘導(dǎo)輪、離心輪、葉輪及大輪盤等構(gòu)成。圖示也給出了坐標(biāo)方向，軸向?yàn)閤向，徑向?yàn)閥、z向。

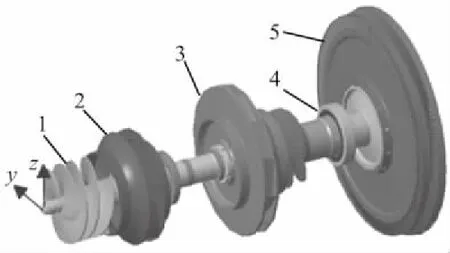
1—誘導(dǎo)輪；2—離心輪；3—中間輪；4—軸承；5—葉輪。圖1 轉(zhuǎn)子結(jié)構(gòu)圖

轉(zhuǎn)子為套裝轉(zhuǎn)子，除輪盤采用螺栓緊緊與轉(zhuǎn)軸相連以外，其他輪件均為單獨(dú)部件，用槽約束其周向位移，軸向與套筒、擋圈等壓緊。

3 基于試驗(yàn)數(shù)據(jù)的有限元模型修正

由于有實(shí)物樣機(jī)，能夠得到可靠的實(shí)驗(yàn)結(jié)果，所以在對轉(zhuǎn)子進(jìn)行動力學(xué)建模的過程中，可以不用建立超模型作為參考，直接建立簡化模型，結(jié)果若偏差過大可以進(jìn)行模型修正，使之與實(shí)驗(yàn)結(jié)果相匹配。

一般對轉(zhuǎn)子進(jìn)行有限元簡化建模，可以考慮將轉(zhuǎn)子分為若干段，在外接輪盤質(zhì)心處、軸承安裝處及轉(zhuǎn)軸徑向結(jié)構(gòu)有較大變動處等部位截斷,然后考慮實(shí)際的幾何結(jié)構(gòu)關(guān)系，考察各部件與轉(zhuǎn)軸之間的物理關(guān)系。對于該轉(zhuǎn)子，各輪部件都是套在轉(zhuǎn)軸上，對轉(zhuǎn)軸的剛性影響很小，故只需考慮它們在節(jié)點(diǎn)處的質(zhì)量和轉(zhuǎn)動慣量，而忽略其剛性的影響。轉(zhuǎn)軸總共有16個節(jié)點(diǎn)，被分為15段。各段軸單元的質(zhì)量、轉(zhuǎn)動慣量與長度均與原有模型保持一致，其楊氏模量則可按照剛度等效的原則計算得到。

對有限元模型進(jìn)行計算分析，對比初始楊氏模量下有限元模型前2階固有頻率計算結(jié)果與實(shí)驗(yàn)結(jié)果。在此基礎(chǔ)上以實(shí)驗(yàn)結(jié)果為基準(zhǔn)進(jìn)行模型修正，得到修正后的楊氏模量。表1給出了修正后前2階固有頻率誤差。

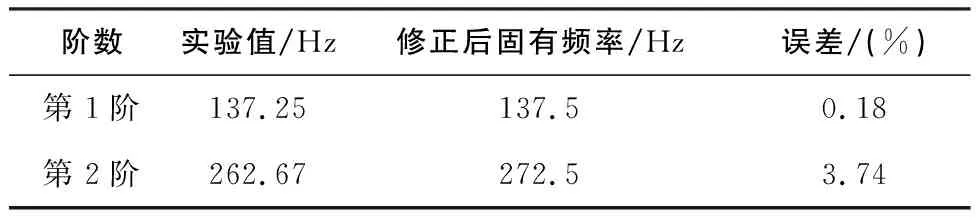
表1 修正后固有頻率誤差

由表1可以看出，修正后模型的固有頻率十分接近實(shí)驗(yàn)值，說明該轉(zhuǎn)子有限元模型可以代替實(shí)驗(yàn)?zāi)Ｐ汀＝又鴮π拚蟮霓D(zhuǎn)子有限元模型進(jìn)行不確定性建模分析。

4 轉(zhuǎn)子動力學(xué)特性的不確定性分析

對于此渦輪泵轉(zhuǎn)子系統(tǒng)來說，中間部分是由大量軸環(huán)套裝在一起的，對其施加預(yù)緊力以壓緊。不同的預(yù)緊力會使中間軸環(huán)部分對該段轉(zhuǎn)軸的剛性造成不同程度的影響，由此會帶來實(shí)際建模過程中的不確定性問題。對此，針對其中環(huán)套2和環(huán)套3影響下轉(zhuǎn)軸的楊氏模量的不確定性，基于PCE法對該轉(zhuǎn)子系統(tǒng)進(jìn)行不確定性分析。

環(huán)套2、環(huán)套3二者綜合影響下的楊氏模量服從正態(tài)分布且波動值均為20%。采取1000個樣本抽樣得到的轉(zhuǎn)子動力學(xué)不確定性頻響曲線結(jié)果如圖2-圖4所示。圖中中間由紅藍(lán)兩條線組成，紅色線代表確定值情況下的結(jié)果，藍(lán)色線代表PCE法抽樣結(jié)果的均值。兩條綠色線則是多項(xiàng)式混沌展開法抽樣計算得到響應(yīng)的最大值與最小值曲線(因本刊為黑白印刷，如有疑問請咨詢作者)。

從圖2-圖4中可以看出，由預(yù)緊力引發(fā)的轉(zhuǎn)軸中間部分剛度的不確定性會引起整個轉(zhuǎn)子系統(tǒng)的不確定。兩個環(huán)套對轉(zhuǎn)子系統(tǒng)的第1階臨界轉(zhuǎn)速的影響很小，對第2階臨界轉(zhuǎn)速的影響則相對較大。受兩個環(huán)套綜合影響的不確定性會呈現(xiàn)出比受單一環(huán)套影響更大的波動。

圖2 渦輪泵轉(zhuǎn)子不確定性頻響曲線(環(huán)套2)

圖3 渦輪泵轉(zhuǎn)子不確定性頻響曲線(環(huán)套3)

圖4 渦輪泵轉(zhuǎn)子不確定性頻響曲線(環(huán)套2和環(huán)套3)

實(shí)際情況中受到影響的轉(zhuǎn)軸剛度不確定性會更多，這種累加效應(yīng)引發(fā)的不確定性的擴(kuò)展會更大，由此會帶來轉(zhuǎn)子設(shè)計過程中的一系列問題。因此在渦輪泵轉(zhuǎn)子動力學(xué)實(shí)驗(yàn)的過程中，應(yīng)當(dāng)考慮中間環(huán)套的預(yù)緊力。

接著考慮環(huán)套2和環(huán)套3綜合影響下的轉(zhuǎn)軸軸段楊氏模量波動值分別為10%和30%的情況。由于主要波動發(fā)生在第2階臨界轉(zhuǎn)速附近，因此統(tǒng)計其附近的不確定影響,包括第2階臨界轉(zhuǎn)速的轉(zhuǎn)速范圍和幅值范圍。經(jīng)計算，第2階臨界轉(zhuǎn)速和幅值的準(zhǔn)確值分別為625.1r/s、2.621×10-4mm。

由圖5可以看出，轉(zhuǎn)速的變化范圍隨著波動值的增加基本呈線性增加，而幅值的變化范圍則呈現(xiàn)非線性。隨著波動的加大，幅值變化的不確定性程度會更顯著。

5 結(jié)語

論文針對火箭發(fā)動機(jī)渦輪泵轉(zhuǎn)子系統(tǒng)的結(jié)構(gòu)特點(diǎn)，以渦輪泵轉(zhuǎn)子中的局部連接結(jié)構(gòu)為研究對象，建立了轉(zhuǎn)子系統(tǒng)的有限元模型，通過與模態(tài)試驗(yàn)結(jié)果對比及模型修正，前2階模態(tài)的頻率誤差不超過4%。首先保證了有限元模型的準(zhǔn)確性，其次將多項(xiàng)式混沌展開法應(yīng)用到局部連接剛度含不確定性參數(shù)的動力特性建模及計算。通過結(jié)果分析可以發(fā)現(xiàn)，采用PCE法計算得到的含不確定性參數(shù)的轉(zhuǎn)子前兩階臨界轉(zhuǎn)速均值十分靠近基準(zhǔn)解，這證明了多項(xiàng)式混沌展開法的正確性。通過結(jié)果波動值的變化又可以看出連接剛度的不確定性在轉(zhuǎn)子系統(tǒng)中呈現(xiàn)不同程度的擴(kuò)展，這也就說明了渦輪泵轉(zhuǎn)子中間軸環(huán)部分預(yù)緊力大小引發(fā)連接剛度的不確定性問題會對轉(zhuǎn)子系統(tǒng)產(chǎn)生不可忽視的影響。

圖5 波動大小對第2階臨界轉(zhuǎn)速的影響