基于模態應力法的副車架疲勞分析研究

王瑋，周肖飛

(1. 西安交通工程學院，陜西 西安 710300； 2. 陜西汽車控股集團有限公司，陜西 西安 710200)

0 引言

汽車結構的可靠性是汽車工程關注的一個重點領域，疲勞性能是影響客戶體驗的重中之重。隨著設計水平的提升，現代汽車結構很少有強度破壞的情況發生，而是汽車在行駛一段里程后出現疲勞破壞。在傳統的疲勞分析中，技術人員采用準靜態的工況評估結構承受單位載荷作用下的應力，然后疊加載荷譜形成應力時間歷程，再通過S-N曲線估算結構承受的損傷[1]，這種方法操作簡單，理論淺顯，被廣泛地應用在汽車結構損傷評估中。但是，汽車在行駛過程中，車身結構所承受載荷是一個動態的過程，在不同頻率下，其響應與靜態響應差異較大，因此，采用靜態方法計算的應力時間歷程并不能真實表達結構的受力。采用瞬態分析直接求解結構的動力學方程固然能夠反映結構真實的應力水平，但其計算過程復雜，耗費的計算成本極高，因此在復雜結構的分析中并不會采用。模態應力法巧妙地避開了上述兩種方法的諸多弊端，能夠在考慮結構動態響應的同時保證計算的效率，并能很好地與試驗對應，逐漸被業界廣泛關注。

1 模態應力法

1.1 模態基礎知識

在無阻尼振動系統中，振動微分方程可表達為[2]

(1)

其中：[M]為質量矩陣；[K]為剛度矩陣；x(t)為位移向量；{f(t)}為載荷向量。

當系統無外力輸入時，系統轉換為自由振動狀態。

假設：

x(t)=Asinωt+φ

(2)

將x(t)代入振動微分方程，方程可變換為

(3)

其中A為振型向量，A=(A1,A2,…,An)。

由于在振動過程中，A1,A2,…,An不能同時為0，所以

(4)

求解此行列式即可得到n個ω值，這些即為此振動系統的固有頻率，它們由系統的剛度和阻尼決定，將ωn代入式(3)，可得到對應的振型向量。對于n個自由度的系統，可以解出n個固有頻率和對應的n個振型向量。

上述結構的振動耦合是在其物理坐標系中發生的，但是利用結構系統的正交特性，可以實現振動的解耦，因為理論上已經證明了各個振型旋轉以后互相正交。為此，引入一組新的坐標ξ=(ξ1,ξ2,…,ξn)，并使新的坐標ξ與原物理坐標y之間構成線性變換，即

(5)

其中：φi為第i階主振型；ξi為第i階模態坐標(modal coordinate)。

這相當于在n維向量空間中(φ1,φ2,…,φn)構成了一組相互正交的向量基，而原物理坐標下定義的n個自由度系統的振動形式，則為n個正交的主振型的線性組合，而ξi則為第i個主振型對系統振動的參與因子。

假設系統阻尼很小，或者阻尼為比例阻尼，則利用上述坐標變換，可以將考慮阻尼的振動方程變換為互相獨立的振動方程的矩陣形式。

(6)

在新的模態坐標下，系統是相互解耦的，每個方程都可以單獨求解，求解后，每個自由度振動方程的解為

(7)

將式(7)代入式(5)，即可解出

(8)

式(8)可以解釋為1個線性系統的振動響應可分解為若干個簡單的單自由度振動響應的疊加。

在工程應用上，不必考慮所有頻率下的振動響應，根據振動力學理論，高頻的激勵對振動能量的貢獻很小[3]，可以忽略不計。此方程即為振型疊加法的基本公式，也是模態結構應力的基本公式。

1.2 模態結構應力的獲取

從1.1中可以得知，結構位移可以表達為主振型和模態參與因子的疊加，那么結構應力同樣可以疊加，由節點位移可以獲得節點應變[4]：

(9)

再由單元本構方程可得[5]

σ=Eε

(10)

其中：σ為節點應力向量；E為材料彈性模量；ε為節點應變。

將方程進行簡化：

σ∝△x

(11)

即節點應力和節點位移的變化成正比，結合1.1中的模態疊加理論，可以將應力表達為

(12)

其中：σ為節點應力向量；σi為第i階模態應力振型；ξi為第i階模態坐標(modal coordinate)。

此方程即為采用模態疊加法獲取結構應力的基本方程。

2 模態應力計算疲勞的有限元實現

采用模態應力法計算結構疲勞損傷可分為3個步驟：

1) 采用模態求解器計算模態應力。

2) 采用模態動力學求解器計算在實際載荷作用下結構的模態坐標響應。

3) 在疲勞分析軟件中將模態應力和模態坐標進行疊加，再通過S-N方法計算結構的疲勞損傷[6]，其分析流程見圖1。

圖1 采用模態應力計算疲勞的分析流程

在常規分析中，一般模態的求解采用NASTRAN 103求解器，模態坐標的求解采用NASTRAN 112求解器，而S-N疲勞分析一般在NCODE中進行實現[7]。

3 基于模態應力的副車架疲勞分析

圖2為某款SUV的前副車架模型，它的主體材料為SAPH400鋼，底板材料為SAPH370，其他附件為鋁材。在該分析中，僅關注主體結構的疲勞損傷性能。

圖2 某車型前副車架模型

該車在環形試驗場中進行了全套道路耐久測試，其工況如表1所示。

表1 道路耐久測試工況

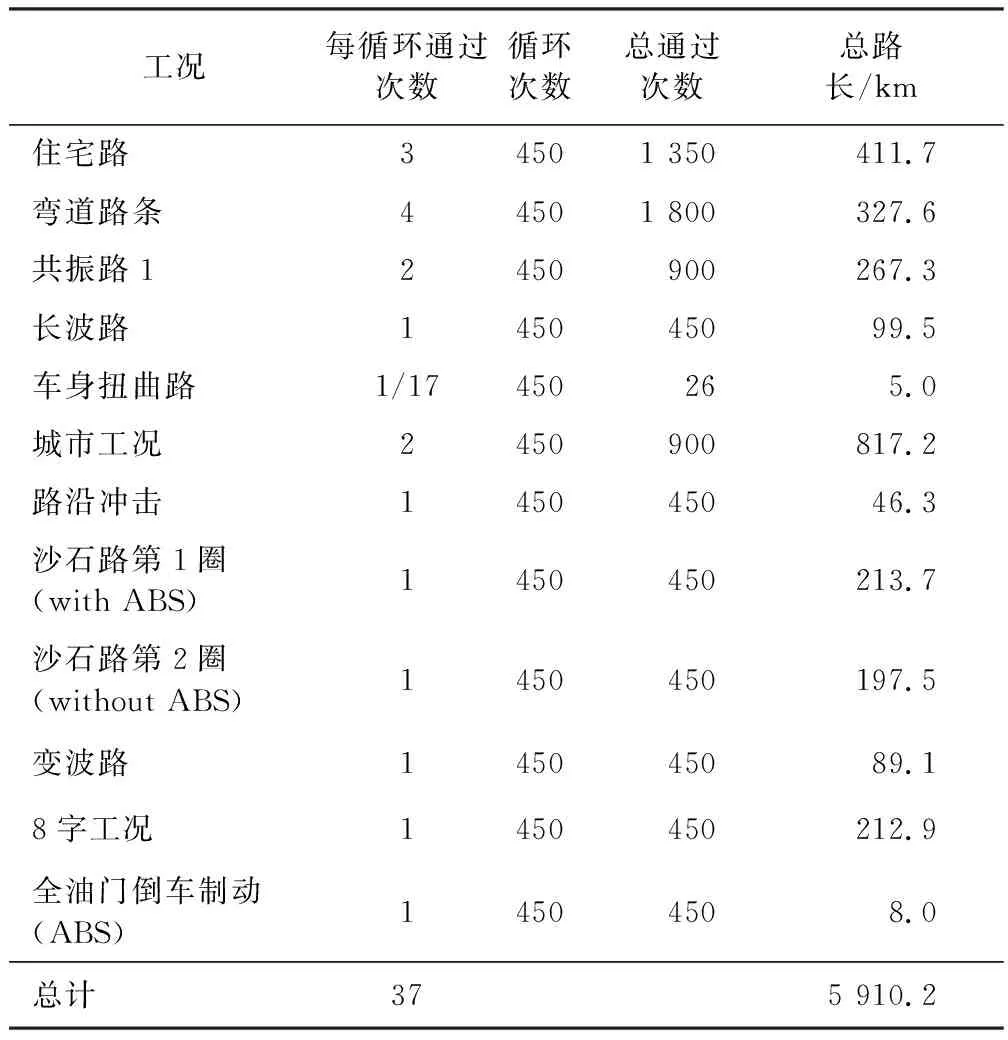
續表1

在進行疲勞分析之前，需要通過多體動力學軟件將載荷進行分解，獲得傳遞到前副車架上的載荷時間歷程，如圖3所示(部分)。

圖3 沖擊路前車身到前副車架左前接附點x,y,z 3向載荷時間歷程

3.1 準靜態疲勞分析

將單位載荷作用下結構的應力響應與疲勞載荷譜進行疊加，獲取應力時間歷程，然后采用S-N方法計算結構的疲勞損傷[7]。其整體損傷分析結果如圖4所示，圖5將最大損傷位置進行了放大。

圖4 副車架整體損傷云圖(max=0.05)

圖5 副車架最大損傷位置(max=0.05)

由圖4和圖5可知，其最大損傷值為0.05，遠小于臨界值1；最大損傷位置位于轉向機安裝支架根部。

3.2 模態應力法疲勞分析

首先對結構做一次模態分析，計算結構在各階固有頻率下的模態應力。由于車身結構的固有頻率和路面載荷一般都處于低頻的范圍，因此提取前200 Hz以內的模態即可。然后在模態分析的基礎上再進行模態動力學分析，在模型上施加通過載荷分析獲得的載荷歷程曲線，選擇輸出模態坐標。最后在疲勞分析軟件中實現模態應力和模態坐標的疊加，獲取結構在瞬態響應下的應力時間歷程，計算疲勞損傷，其整體損傷結果如圖6所示，圖7將最大損傷位置進行了放大。

圖6 副車架整體損傷云圖(max=1.43)

圖7 副車架最大損傷位置(max=1.43)

由圖6和圖7可知，該副車架在完成全套耐久測試后，其最大損傷值為1.43；超過了臨界值1；最大損傷位置位于轉向機安裝支架根部。

3.3 計算對比分析

對比兩種分析方法的損傷云圖可以看出，采用模態應力法的損傷值和損傷面積要明顯大于采用準靜態方法的結果，對副車架的關鍵點損傷結果進行數據對比，見表2。

表2 副車架關鍵點的損傷值對比

從結果對比可以看出：

1) 采用準靜態方法分析的結果全部滿足使用壽命要求，其最大值為0.05。采用模態應力法的分析結果在局部出現了損傷大于1的情況，說明其壽命不足。

2) 從整體結果來看，采用模態應力法計算結構損傷要遠大于準靜態的分析結果，但結果對比并不會呈現出線性關系。這是因為在結構局部剛度不同，導致對激勵的響應并不會出現按比例放大的特性。

3) 在實際路試中，由于路況比較嚴苛，一般副車架都會出現輕微的損傷開裂情況，這說明，準靜態方法在處理疲勞損傷的過程中，其分析結果偏保守，不能充分避免設計的缺陷。

4 結語

在工程中，大多數工況都是動態的，在某些特定條件下(如加載時間很長，質量極小等)，結構的響應可以采用準靜態的方法進行近似，這對于簡化分析流程和減小數據輸入都很有幫助。但對于頻率較高的激勵(>20 Hz)，會帶來較大的誤差。采用模態應力法既能考慮動態響應的影響，也能排除高頻激勵(>200 Hz)的影響，同時并不會增加計算成本，對提高計算精度，協助車身結構設計都有很好的幫助。