剛體空間定位問題的最優(yōu)控制研究

王麗，蔡鎖寧

(1. 陜西工業(yè)職業(yè)技術(shù)學(xué)院,陜西 咸陽 712000； 2. 陜汽集團(tuán)商用車有限公司，陜西 寶雞 722405)

0 引言

四元數(shù)代數(shù)理論是表示有限轉(zhuǎn)動(dòng)的最簡(jiǎn)明方法，因而四元數(shù)在剛體定點(diǎn)轉(zhuǎn)動(dòng)和球面機(jī)構(gòu)的運(yùn)動(dòng)學(xué)、動(dòng)力學(xué)及其控制問題的研究中得到了廣泛的應(yīng)用。KIUMARSI B[1]針對(duì)存在輸入約束的確定性非線性離散時(shí)間跟蹤控制問題，提出了一種部分無模型自適應(yīng)最優(yōu)控制方法。XIAO G[2]構(gòu)造了由誤差系統(tǒng)動(dòng)力學(xué)和期望軌跡動(dòng)力學(xué)組成的增廣系統(tǒng),研究了一類完全未知?jiǎng)討B(tài)仿射非線性連續(xù)時(shí)間系統(tǒng)的最優(yōu)跟蹤控制問題。KONG Xianwen[3]以四元數(shù)代數(shù)和幾何分析方法給出了歐拉參數(shù)表示的并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)方程及可操作模式。趙金剛[4]針對(duì)運(yùn)動(dòng)規(guī)劃的非完整性問題，引入效用函數(shù),實(shí)現(xiàn)了非完整運(yùn)動(dòng)規(guī)劃的最優(yōu)控制。彭海軍[5]利用多體動(dòng)力學(xué)建立系統(tǒng)的動(dòng)力學(xué)方程，通過引入對(duì)目標(biāo)軌跡跟蹤及瞬時(shí)最優(yōu)性能指標(biāo)，獲得最優(yōu)控制量。屈秋霞[6]針對(duì)非線性連續(xù)系統(tǒng)難以跟蹤時(shí)變軌跡的問題,通過系統(tǒng)變換將其轉(zhuǎn)化為非線性時(shí)不變系統(tǒng)的最優(yōu)控制問題。賈意弦[7]采用四元數(shù)描述剛體姿態(tài)運(yùn)動(dòng)，避免了歐拉角存在的奇異性。史革盟[8]用四元數(shù)表示構(gòu)件的有限轉(zhuǎn)動(dòng)，得到四元數(shù)形式的運(yùn)動(dòng)方程。李保坤[9]以單位四元數(shù)描述剛體的姿態(tài),導(dǎo)出Stewart機(jī)構(gòu)處于給定位置時(shí)的姿態(tài)奇異表達(dá)式。程世利[10]采用四元數(shù)表示旋轉(zhuǎn)變換，得到并聯(lián)機(jī)構(gòu)四元數(shù)形式的基本方程和奇異方程。本文將四元數(shù)代數(shù)理論用于剛體的姿態(tài)定位控制，通過不動(dòng)點(diǎn)穩(wěn)定性分析得到解軌線在狀態(tài)空間的變化趨勢(shì)及收斂域，建立大范圍漸近穩(wěn)定控制的條件，從微分幾何的角度，分析剛體定位過程解軌線的幾何約束，構(gòu)造最短路徑控制的目標(biāo)泛函，實(shí)現(xiàn)了剛體的快速定位。

1 剛體有限轉(zhuǎn)動(dòng)運(yùn)動(dòng)學(xué)方程

根據(jù)剛體無限小旋轉(zhuǎn)變換[11]，得式(1):

(1)

式中：ξ為四元數(shù)Λ矢量方向的單位矢量；Δθ、ω分別為剛體的無限小轉(zhuǎn)角和角速度。

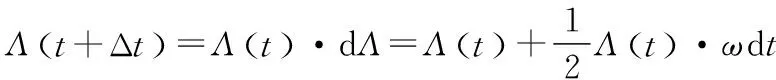
由上式可得剛體有限轉(zhuǎn)動(dòng)運(yùn)動(dòng)方程：

(2)

按四元數(shù)乘積展開上式，得到四元數(shù)分量形式的一階線性微分方程組：

(3)

2 空間定位問題的運(yùn)動(dòng)學(xué)穩(wěn)定控制

2.1 運(yùn)動(dòng)學(xué)漸近穩(wěn)定控制的條件

空間定位問題就是改變剛體的角速度ωE，使得與其固連的坐標(biāo)系E與參考坐標(biāo)系I方向一致。

(4)

為了滿足式(4)給出的快速定位條件，就要求式(3)中的后3個(gè)關(guān)于λi(i=1,2,3)的微分方程具有李雅普諾夫意義下全局漸近穩(wěn)定的動(dòng)態(tài)特性。取李雅普諾夫函數(shù)

對(duì)時(shí)間t求導(dǎo)，并代入式(3)中的關(guān)系

(5)

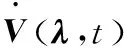
ωi=-kiλ0λii=1,2,3

(6)

式中ki為角速度修正系數(shù)。當(dāng)ki>0時(shí)，

(7)

符合全局漸近穩(wěn)定條件，式(3)后3個(gè)狀態(tài)方程能從任意初始狀態(tài)收斂到原點(diǎn)。

2.2 狀態(tài)空間不動(dòng)點(diǎn)穩(wěn)定性分析

將式(6)代入式(3)可得狀態(tài)方程：

(8)

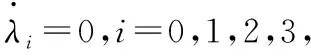
根據(jù)非線性微分方程理論，狀態(tài)方程解分量λi(t),(i=0,1,2,3)都是時(shí)間的單調(diào)增函數(shù)或單調(diào)減函數(shù)，由于四元數(shù)Λ范數(shù)恒等于1，其分量函數(shù)λi(t)為有界函數(shù)，|λi(t)|≤1，因而從任意初始狀態(tài)出發(fā)的解軌線都將趨近并終止于某個(gè)不動(dòng)點(diǎn)。

1)ki>0,?i=1,2,3

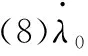
(9)

狀態(tài)方程的解軌線都將趨近并穩(wěn)定到第2類不動(dòng)點(diǎn)[1,0,0,0]T或[-1,0,0,0]T。

2)ki<0,?i=1,2,3

(10)

狀態(tài)方程的解軌線都將趨近并穩(wěn)定到第1類不動(dòng)點(diǎn)[0,λ1,λ2,λ3]T。

3 剛體定位問題最短路徑控制

在如上漸進(jìn)控制中，收斂速度取決于修正系數(shù)ki的取值大小，這會(huì)導(dǎo)致定位過程僅是一種可達(dá)路徑并非最短路徑。將狀態(tài)方程的解軌線看作狀態(tài)空間的參數(shù)曲線

r(t)=[λ0(t),λ3(t),λ3(t),λ3(t)]T

(11)

(12)

定位軌線最短路徑即是沿超球面上過這兩點(diǎn)所在的大圓的劣弧到達(dá)目標(biāo)點(diǎn)M。超球面上各點(diǎn)向徑具有固定長(zhǎng)度:

解軌線切向量始終與向徑正交。將式(3)的定位過程解軌線弧長(zhǎng)取為性能指標(biāo)泛函

(13)

式中t0、tf分別為初始和末態(tài)時(shí)刻。末態(tài)時(shí)刻tf不確定，末態(tài)固定λ(tf)=[1,0,0,0]T；L為拉格朗日函數(shù)。

引入狀態(tài)約束的拉格朗日乘子η(t)，將被控系統(tǒng)狀態(tài)方程式(3)和性能指標(biāo)泛函結(jié)合成輔助泛函

式中H為哈密頓標(biāo)量函數(shù)。

H[λ(t),ω(t),ηT(t),t]=L[λ(t),ω(t),t]+ηT(t)f[λ,ω，t]

將J對(duì)所有變量tf、λ、ω、η進(jìn)行變分：

δJ={H[λ(t),ω(t),ηT(t),t]}t=ffδtf+

根據(jù)泛函極值的必要條件δJ=0可得:

1) 規(guī)范方程及邊界條件

(14)

(15)

(16)

2) 極值條件

(17)

從中求得控制量

ω(t)=-|ω(t)|FTη(t)

(18)

代入規(guī)范方程式(14)和式(15)得最短路徑控制的狀態(tài)方程:

(19)

(20)

定位過程的弧長(zhǎng)只與解軌線的路徑有關(guān)，因而角速度|ω(t)|可以取任意正實(shí)數(shù)。

4 應(yīng)用實(shí)例

假設(shè)初始時(shí)刻與剛體固連的動(dòng)坐標(biāo)系對(duì)參考坐標(biāo)系的偏差四元數(shù)

Λ(t0)=[0.36,-0.30,0.48,-0.73]T

取角速度修正系數(shù)k1=4.0,k2=6.0,k3=8.0，求解剛體運(yùn)動(dòng)微分方程式(8)，得到偏差四元數(shù)的解軌線變化趨勢(shì)，如圖1所示。

圖1 偏差四元數(shù)的解軌跡

偏差四元數(shù)的分量以近似于指數(shù)函數(shù)的速度趨近目標(biāo)值，在控制作用2s后，偏差縮小到10-6的范圍之內(nèi)。為了驗(yàn)證不動(dòng)點(diǎn)的穩(wěn)定性，取狀態(tài)空間某個(gè)半徑0<|r(t)|<1超球面上的點(diǎn)作為初始偏差，求解剛體狀態(tài)空間方程式(8)的解軌線，給出了解軌線在λ0-λ1平面上的投影。當(dāng)ki>0,?i=1,2,3，對(duì)于所有初始偏差λ0<0解軌線都趨近并穩(wěn)定到第2類不動(dòng)點(diǎn)[-1,0,0,0]T，對(duì)于所有λ0>0解軌線都趨近并穩(wěn)定到第2類不動(dòng)點(diǎn)[1,0,0,0]T，它們是穩(wěn)定的不動(dòng)點(diǎn)，如圖2所示。當(dāng)ki<0, ?i=1,2,3，所有解軌線都趨近并穩(wěn)定到第1類不動(dòng)點(diǎn)[0,λ1,λ2,λ3]T，如圖3所示。

圖2 狀態(tài)空間穩(wěn)定的第2類不動(dòng)點(diǎn)

圖3 狀態(tài)空間穩(wěn)定的第1類不動(dòng)點(diǎn)

對(duì)剛體按式(19)和式(20)的規(guī)范方程及其邊界條件式(16)進(jìn)行最優(yōu)控制，得到偏差四元數(shù)的解軌線，如圖4所示。

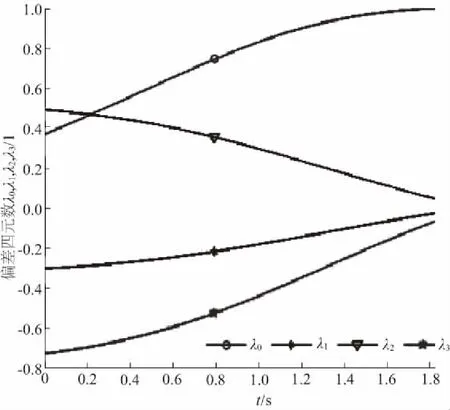
圖4 最優(yōu)控制下偏差四元數(shù)的解軌線

5 結(jié)語

1) 利用四元數(shù)分量表示純轉(zhuǎn)動(dòng)剛體定位偏差，并作為被控制量實(shí)現(xiàn)對(duì)剛體有限轉(zhuǎn)動(dòng)進(jìn)行大范圍漸進(jìn)穩(wěn)定的控制。

2) 對(duì)狀態(tài)方程不動(dòng)點(diǎn)的穩(wěn)定性分析，得到剛體定位過程中狀態(tài)方程的解軌線在不動(dòng)點(diǎn)鄰域的變化趨勢(shì)，導(dǎo)出剛體趨近并定位到目標(biāo)姿態(tài)的收斂條件。結(jié)果表明，定位過程被控制量以指數(shù)函數(shù)的速度趨近目標(biāo)值。

3) 結(jié)合剛體定位和姿態(tài)控制問題的一般特點(diǎn)，從微分幾何的角度，分析了定位過程解軌線滿足的幾何約束，構(gòu)造出量化最短路徑控制的目標(biāo)泛函，導(dǎo)出最優(yōu)控制應(yīng)該滿足的狀態(tài)方程、邊界條件和極值條件，進(jìn)而將剛體定位最優(yōu)控制問題處理為一階非線性微分方程的兩點(diǎn)邊值問題。