一種VSSFxLMS算法及其在多自由度微振動控制中的應用

方昱斌 朱曉錦 胡佳明 高志遠 苗中華

摘要：FxLMS算法常用于自適應振動控制研究領域，其固定步長導致不能同時獲得快的收斂速度和小的穩態誤差。針對多自由度壓電結構振動主動控制，提出一種改進VSSFxLMS振動控制算法，通過利用反余切函數的特性優化算法步長的迭代規律，有效提升算法對于噪聲干擾的魯棒性，并給出該算法的動態性能與穩態性能分析。以壓電結構微振動多通道控制為目標，在ADAMS軟件中建立結構微振動主動控制仿真模型，通過與SIMULINK聯合仿真觀察振動控制算法實施效果。構建了基于壓電堆作動器的多自由度主動隔振結構，以及相關測控單元與實驗系統，進行了結構微振動主動控制實驗與結果分析，驗證了所提出振動控制算法的良好控制效果和魯棒性。

關鍵詞：微振動主動控制;變步長（VSS）;LMS算法;多輸入多輸出（MIMO）;壓電結構

中圖分類號：TB535;TH113.1文獻標志碼：A 文章編號：1004-4523（2020）03-0467-10

DOI：10.16385/j.cnki.issn.1004-4523.2020.03.004

引言

近些年，航天事業及精密制造技術得到迅速發展，涉及到一些精密設備的微振動控制問題，引起了廣泛關注。例如衛星搭載的觀測相機、精密制造中的投射電鏡和掃描電鏡、納米研發裝置等，其工作環境容許的振動速度低于10um/s，要想抑制這樣水平的微振動，通常的被動隔振手段難以實現。基于壓電機敏器件的特性，配合先進的結構振動主動控制方法與快速提升的計算力，使得精密裝置的結構微振動主動控制成為可能。

針對結構微振動主動控制問題，各研究團隊設計出多種微振動模擬平臺或者是微振動隔振平臺，用于實驗室中微振動環境的模擬及微振動主動控制系統的設計驗證。多數微振動隔振試驗臺都采用了Stewart結構，能夠實現多個自由度上的微振動抑制，但是該結構的6個作動器之間具有較強的耦合，運動解耦比較復雜，導致控制系統的設計實施變得相對困難。

為了模擬多自由度微振動實驗環境，并驗證主動振動控制算法的性能，本文設計了一臺3自由度壓電微振動主動控制實驗隔振結構，并構建了相應測控單元及完成軟硬件開發，可以實現結構微振動多自由度主動控制算法的實施與驗證。同時，針對實驗隔振結構的機械設計環節，將多個作動器之間的耦合隔離，有利于復雜控制算法的設計實施和效果驗證。

對于結構微振動主動控制方法，現有研究已經涉及了極點配置、最優控制、魯棒控制和自適應控制等諸多控制理論方法，各種方法的具體應用也各有其特點和局限。考慮到一些復雜設備與裝置可能存在的結構非線性與時變環節，自適應振動控制方法具有較好的技術特點與優勢，尤其在自適應噪聲與結構振動主動控制領域，基于自適應濾波算法的相關控制方法研究更為廣泛。當前，自適應濾波振動主動控制算法主要包括濾波-X最小均方算法（Filtered-X Least Mean Square，FxLMS），濾波X遞推最小二乘算法（Fihered-X Recursive LeastSquares，RLS）、快速橫向濾波算法（Fast Transver-sal Filtcr，FTF）等。FxLMS算法因其算法簡單、收斂速度快等優點被普遍使用。但是FxLMS算法在參數自適應調節時所采用的傳統固定步長最小均方（LMS）算法，很難同時保證收斂速度和穩態精度，因此學者們提出了變步長最小均方（VariablcStep Size LMS，VSSLMS）改進算法，其主要思想是在算法的收斂初期采用較大步長以提高收斂速度，而在穩態附近時采用較小步長以減小穩態誤差。

事實上，從第一個VSSLMS算法被提出至今，已經有數十種VSSLMS算法問世，并且仍在持續研究中。對現有VSSLMS算法的步長因子更新機理加以分析，VSSLMS算法可以分為三類。

第一類是基于歸一化形式的VSSLMS算法，通過對步長除以輸入信號的二范數，以增加算法對于輸入信號幅值變化的魯棒性。但是這樣的處理會影響到算法的收斂速度及其實時性，不適于應用在嚴實時性及要求快速收斂的系統中。第二類是由覃景繁等提出的一種基于Sigmoid函數的VSS-LMS算法，其根據Sigmoid函數的曲線特性來調節步長因子的變化;在這種算法的機理上，后續又有學者提出了基于箕舌線的VSSLMS算法、基于正弦函數的VSSLMS算法、基于反正切的VSSLMS算法等;這類算法整體來說對于函數曲線的依賴比較嚴重，使其對于具體應用系統的調節不夠靈活。第三類是以Kwong等為代表所提出的算法，該類算法以瞬時誤差控制步長因子的更新，并通過遺忘因子來減弱之前時刻誤差的權重值;由于誤差信號采集過程中會引入不同程度的噪聲，步長因子迭代必然會受到影響，這使得算法的穩態精度不易得到保證。

對于文獻提出的VSSLMS算法，其依據系統瞬時誤差的平方值迭代更新算法收斂步長，相比于傳統LMS算法，對躍變的跟蹤能力得到提升，但是其抗干擾能力仍欠佳。文獻對此做了相關改進，利用系統誤差與其前一采樣的系統誤差的自相關估計來更新收斂步長，提升了算法對于噪聲干擾的魯棒性。文獻對文獻中的算法做了簡化改進，在保持算法性能的同時減少了迭代計算量，增加了算法在實時系統中的應用優勢。

此外，大部分VSSLMS算法都是基于系統辨識和主動噪聲控制應用設計提出的，與其在結構振動主動控制研究中的應用有所差異。對于結構振動主動控制應用，在收斂過程中系統可能會受到外界瞬時強烈的寬頻噪聲干擾，使得VSSLMS算法產生較大步長，控制器輸出過大的作動信號，反而會引起穩態附近的大幅振動，對系統穩定性造成不利。因此，若要將VSSLMS算法應用在結構振動主動控制中，對于噪聲干擾的魯棒性需要認真考慮。

針對結構微振動主動控制應用的特點，本文提出一種VSSLMS算法，該算法利用反余切函數的特性，針對文獻[18]中提出的算法進行了改進，建立了瞬時誤差與步長因子之間的非線性函數關系，使得算法在收斂速度與精度之間達到平衡，并且對于噪聲具有較好的魯棒性;在此基礎上，在ADAMS中建立基于壓電堆作動的3自由度微振動主動控制仿真模型，通過SIMULINK與ADAMS的聯合仿真，驗證了所提出算法在濾波-X前饋結構中的收斂性;最后，構建基于多自由度壓電隔振結構的微振動主動控制實驗平臺，通過不同條件下結構微振動多通道控制實驗，對比驗證了改進變步長濾波-X最小均方（Variable Step Size Filtered-x Least MeanSquare，VSSFxLMS）算法在結構微振動主動控制中的有效性和魯棒性。

1VSSLMS算法的提出

在本節中，將文獻[18-20]中的VSSLMS算法的步長更新公式做簡要介紹，并對其每次步長迭代中所需要調節的參數個數以及計算量做了對比，如表1所示。為了方便表示，下文中將文獻中的VSSLMS算法分別表示為VSSLMS-A，VSS-LMS-B和VSSLMS-C，將改進算法命名為VSS-LMS-New。

VSSLMS-A的步長直接依據瞬時誤差更新，在結構振動控制系統中瞬時誤差值是在不斷振蕩變化的。同時，還會有噪聲干擾引起的結構振動，這會使得算法步長變化對于系統噪聲干擾比較敏感，從而會引起控制器的輸出波動甚至大幅波動，穩態中的系統會因此增加穩態誤差甚至跳出穩態直至發散。VSSLMS-A算法中共有2個調節參數ξ和η，其中0<ξ<1，η>0;參數ξ是遺忘因子，決定過去時刻步長在迭代中的權值，參數η控制算法的調節速度及穩態誤差。

VSSLMS-B中的步長通過系統誤差e（n）及其前一采樣時刻系統誤差e（n-1）的自相關系數估計值計算得到。引入誤差的自相關系數，可以減弱噪聲干擾對于系統收斂步長的影響，從而增加算法對噪聲干擾的魯棒性。VSSLMS-B有3個調節參數ξ，η和λ。ξ和η的取值范圍和作用與VSSLMS-A相同，參數λ（0<λ<1）是平均時間常量的遺忘因子，決定過去時刻的采樣信息對當前估計值的影響權重。雖然該算法一定程度上提升了VSSLMS-A對于噪聲干擾的魯棒性，但是增加了一個調節參數，每次迭代中增加了3次乘法運算和1次加法運算，這對于實時系統尤其是多輸入多輸出實時系統來說可能會影響其實時性。

VSSLMS-C對VSSLMS-B做了簡化，略去加權因子入，僅需要2個調節參數，且步長更新的每次迭代僅需要4次乘法運算和1次加法運算，增加了該算法在實時控制應用中的優勢。文獻[20]通過仿真表明了VSSLMS-C與VSSLMS-B在傅里葉分析中具有幾乎相同的收斂性能，但該算法并未在結構振動主動控制研究中進行過驗證。

VSSLMS-A中步長迭代更新量為，ηe²（n），因為參數η是個固定值，則除去遺忘因子的衰減作用之外，步長增量主要受誤差e（n）影響。當e（n）在0附近振蕩時，下一步迭代的步長增量就會很小，這在算法收斂初期很影響收斂速度。在算法收斂至穩態時，e（n）受到噪聲或者擾動的影響導致瞬時值變大，則引起步長瞬間增大，會導致系統脫離穩態重新振蕩。

利用反余切函數的特性，將VSSLMS-A中的迭代更新參數刀改進為與誤差信號相關的變量η（n）=βarccot（| e（n）|），則可以大幅改善上述情況。在收斂初期，參數η（n）會削弱誤差信號e（n），振蕩帶來的收斂速度減緩，保證算法快速收斂;在穩態時，參數η（n）能夠抑制噪聲干擾等導致的誤差瞬時值突變所帶給系統穩態的影響，提升穩態時算法的魯棒性。

針對結構振動主動控制系統，提出一種改進VSSLMS算法，以增強算法對噪聲干擾的魯棒性。VSSLMS-New的步長更新公式如下式所示：

相比于VSSLMS-A，VSSLMS-New中的參數η（n）是一個基于反余切函數性質的時變參數，暫叫做步長抑制因子。步長抑制因子η（n）利用反余切函數的性質，可以在誤差信號突變時抑制步長的突變，提高算法對于噪聲的魯棒性。

在VSSLMS-New中，步長迭代包含有2個調節參數ξ和β。其中，ξ與VSSLMS-A中作用相同，取值范圍0<ξ<1;β（β>0）為縮放因子，根據實際系統中誤差信號數值的數量級進行配置。在步長的每次更新迭代中，VSSLMS-New需要4次乘法運算和1次加法運算，與VSSLMS-C相同，比VSS-LMS-B少2次乘法運算和1次加法運算。與VSS-LMS-A算法相比，所需調節的參數個數相同，每次迭代需要多1次乘法運算。

2 VSSLMS-New算法分析

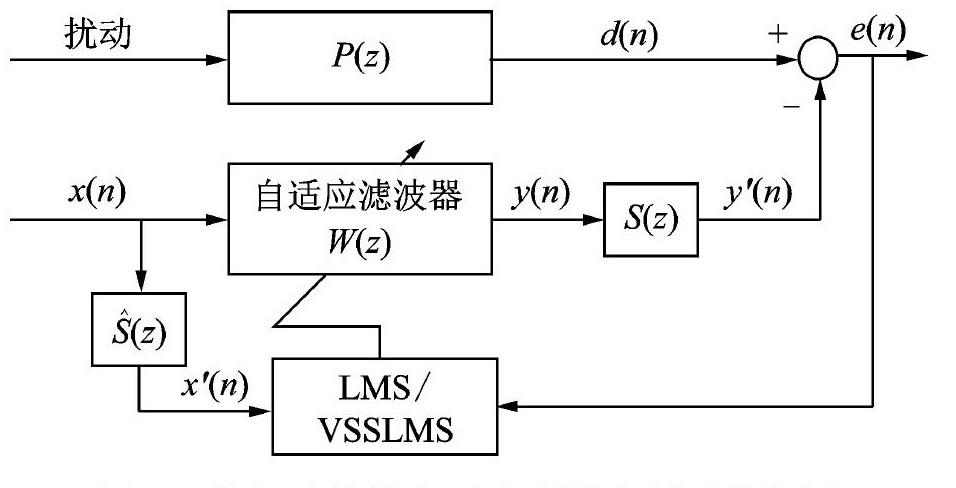
如圖1所示，在自適應濾波過程中，依據梯度下降法可得到VSSLMS算法自適應濾波器的權值遞推如下式所示：

式中 w（22）為自適應濾波器權值向量，w_*（n）為最優濾波器權值向量，x（n）為輸入信號序列，d（n）為擾動在主通道的響應，y（n）為自適應濾波器的輸出，e（n）為誤差信號，n為離散時間序列，u（n）為時變步長因子，ξ（n）為零期望的測量噪聲信號，符合白噪聲特點。

為了方便分析，假設輸入信號序列x（n）符合高斯分布，期望為0.則輸入信號的自相關矩陣定義為R=E[x（n）x^T（n）]，可以寫成R=QAQ^T，其中A為特征值矩陣。假設最優濾波器權值向量w*（n）的階數與系統真實模型相同，即w*（n）能夠準確表示實際系統。

2.1 平均意義下的動態分析

根據VSSLMS-New算法的步長更新公式，將式（3）-（5）代入式（1）可得下式

式中 V（n）=w（n）-w*（n），V（n）表示自適應濾波器權值向量偏差，V（n）=Q^TV（n），x（n）=Q^Tx（n）。

通常，參數η（n）的值比較小。所以，相比于誤差信號e（n）和輸入序列x（n），步長因子u（n）的變化是很緩慢的。因此，可以認為步長因子u（n）與其自身平方u²（n）、誤差信號e（n），自適應濾波器權值向量w（n）以及輸入序列x（n）都相互獨立，則濾波器權值向量期望收斂的一個充分條件為式中 λ_max（R）是矩陣R的最大特征值。

2.2 均方意義下的動態分析

誤差信號的均方差（mean square error，MSE）定義如下式所示