纖維混凝土組合橋面板裂縫寬度計算方法

戴昌源，蘇慶田，馮小毛，周小勇，徐 晨

（1.同濟大學土木工程學院，上海200092；2.江西省高速集團有限公司，江西南昌330025）

隨著組合橋面板技術日趨成熟，越來越多的橋梁采用了這種橋面形式。它可以有效降低橋面板鋼結構中的應力，減少鋼橋面板疲勞發生的風險。同時由于橋面板剛度較大，也避免了鋪裝層的開裂等耐久性問題。邵旭東［1］、楊勇［2］、聶建國［3］、蘇慶田［4-5］等學者提出了多種組合橋面板的構造形式，其中多數都得以在實際工程中應用。

組合橋面板的雛形是在正交異性鋼橋面板上做一層常規混凝土面層［6］。當組合橋面板處于整體結構的負彎矩區或局部負彎矩區時混凝土會出現開裂問題，在設計中通過限制結構在正常使用極限狀態下的裂縫寬度值來保證結構的耐久性。纖維混凝土（包括纖維高強混凝土和超高性能混凝土UHPC）有較強的抗裂性與韌性，應用于橋面結構后可以有效限制裂縫發展，提高結構耐久性。盡管如此，對纖維混凝土組合橋面結構的裂縫寬度預測仍然有十分重要的意義，這可以使設計人員對于結構中纖維參量、纖維尺寸、配筋率等參數做出較為準確的計算，從而使結構布置趨于合理。

此前許多學者［7-11］對不同纖維參量、纖維種類、多種纖維混雜、受疲勞荷載作用等的纖維混凝土進行研究，結果表明纖維對裂縫的抑制作用是由于開裂后鋼纖維對裂縫兩側混凝土有橋接作用，在開裂后的斷面中仍然存在一定等效殘余應力。因此，為了準確預測纖維混凝土結構在開裂后的各種響應——例如裂縫寬度，對上述殘余應力的合理取值必不可少。

目前確定纖維混凝土開裂后殘余應力的方法主要是通過試驗。國內針對纖維混凝土組合結構的設計規范有《纖維混凝土結構技術規程》［12］（CECS 38：2004）（后簡稱《規程》）。《規程》中建議在進行正常使用階段設計時應按照現行混凝土設計規范計算不考慮纖維作用的混凝土構件最大裂縫寬ωmax，在此基礎上乘以考慮纖維作用的折減系數（1-βewλf）得到纖維混凝土正常使用階段的裂縫寬度預測值。此折減系數中的βew建議通過試驗獲得，缺少試驗數據且混凝土等級不高于CF45時建議采用規范中提供的經驗值。《規程》中考慮的參數較少，很難考慮市場上多種形狀的纖維，而不同形狀的纖維在混凝土開裂后發揮的作用也不盡相同。歐洲在2010年修訂fib模式規范［13］時加入了針對纖維混凝土結構的設計方法。模式規范建議通過缺口梁試件的三點加載試驗得到纖維混凝土開裂后殘余應力—裂縫寬度曲線，繼而算出正常使用極限狀態計算公式中需要考慮的纖維殘余應力均值fFtsm。近期的研究表明常規缺口梁三點加載試驗由于試件尺寸較小，構件邊界會對內部纖維的方向造成較大影響，使其更傾向于平行于構件軸線，得到偏不安全的結果［14］。

針對上述問題，基于歐洲規范4［15］提出了一種針對纖維混凝土組合橋面板負彎矩區開裂后裂縫寬度的完全理論化的預測方法，以纖維長度、直徑、彎鉤尺寸、混凝土強度等級等為參數，利用纖維的空間分布［16-19］和單根纖維的拔出［20-26］等方面的研究成果確定影響殘余應力的主要變量，將這些主要變量對文獻中記載的試驗數據進行回歸分析得到殘余應力的預測公式，并在相應的裂縫寬度計算方法中考慮此殘余應力的有利作用。最后通過一組組合橋面板負彎矩加載試驗對此計算方法進行驗證。此方法省去了試驗確定殘余應力的過程，提供了一定的便利。為在設計中考慮纖維混凝土中鋼纖維的有利作用提供另外一種計算思路。

上述的研究主要針對混凝土構件開展的，對于橋梁結構中的新型鋼纖維混凝土組合橋面板裂縫計算方法還未見報道。因此，本文對組合橋面板中考慮纖維作用的纖維混凝土裂縫計算分析方法進行研究。

1 裂縫寬度計算方法

研究表明［27-28］，纖維混凝土的抗壓性能、彈性模量等參數與常規混凝土相近，而抗拉性能成為其區別常規混凝土的重要方面。本文在歐洲規范4［15］中對組合結構正常使用極限狀態裂縫寬度驗算方法的基礎上，考慮纖維的有利作用，提出了一種纖維混凝土組合橋面板正常使用極限狀態裂縫寬度的驗算方法。

1.1 裂縫寬度

歐洲規范4［15］裂縫寬度的計算公式引用了歐洲規范2［29］，但在鋼筋應力計算中考慮組合結構的受力特點。歐洲規范2［29］中裂縫寬度定義為鋼筋與混凝土的平均應變差值乘以裂縫間距，如式（1）和式（2）所示。

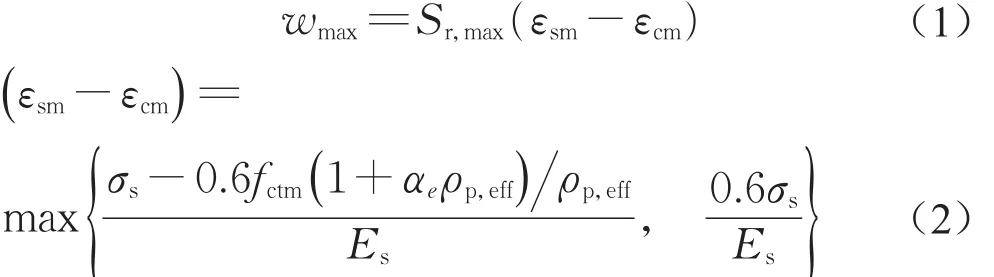
式中：Sr，max為裂縫間距；εsm為鋼筋平均應變，需計入受拉剛化效應；εcm為裂縫間混凝土的平均應變，（εsm-εcm）可由式（2）計算。σs為鋼筋應力；后一項0.6fctm（1+αeρp，eff）/ρp，eff為裂縫產生瞬間裂縫處的最大鋼筋應力，其中0.6為短期荷載的經驗系數，用以得到裂縫間距范圍內的平均應變；αe為鋼筋與混凝土的彈模比；Es為鋼筋彈性模量；ρp，eff為有效受拉斷面的配筋率，對于組合橋面板有效受拉斷面可取整個混凝土斷面；fctm為混凝土抗拉強度平均值。

對于纖維混凝土，由于開裂后鋼纖維承擔了一定的力，鋼筋所承擔的力較尺寸相同的常規鋼筋混凝土小，所以式（2）需要做出相應的修正以考慮纖維的作用。首先對于裂縫產生瞬間裂縫處的最大鋼筋應力 fctm（1+αeρp，eff）/ρp，eff，常規混凝土開裂瞬間原來由混凝土承擔的力fctmAc全部轉由鋼筋承擔，而對于纖維混凝土，由于殘余應力fFtsm的存在，開裂后能夠傳遞大小為fFtsmAc的力，所以傳遞到鋼筋上的力降低為（fctm-fFtsm）Ac。因此，此項修正為（fctm-fFtsm）（1+αeρp，eff）/ρp，eff。

1.2 鋼筋應力

歐洲規范4［15］中，給出組合結構鋼筋應力的計算方法，由兩項構成，如式（3）所示，σs，0是按照開裂截面的特性和斷面所承受的彎矩直接計算的應力。對于鋼纖維混凝土，由于開裂面位置的鋼纖維可以承受一定的力，因此開裂面位置的鋼筋應力較常規混凝土結構會相應減小。鋼纖維在整個斷面中的作用可以分為彎矩作用Mf和軸力Ff作用，若整個截面承受的彎矩為Mout，軸力為0，那么開裂斷面（不包括混凝土）所承受的彎矩為Mout-Mf，軸力為-Ff。由此，可通過式（4）計算不考慮受拉剛化效應的開裂斷面鋼筋應力；Δσs是由于受拉剛化效應開裂截面鋼筋所承受的額外應力，同樣由于纖維的作用，使得受拉剛化效應減弱，修正后的值按式（5）計算。

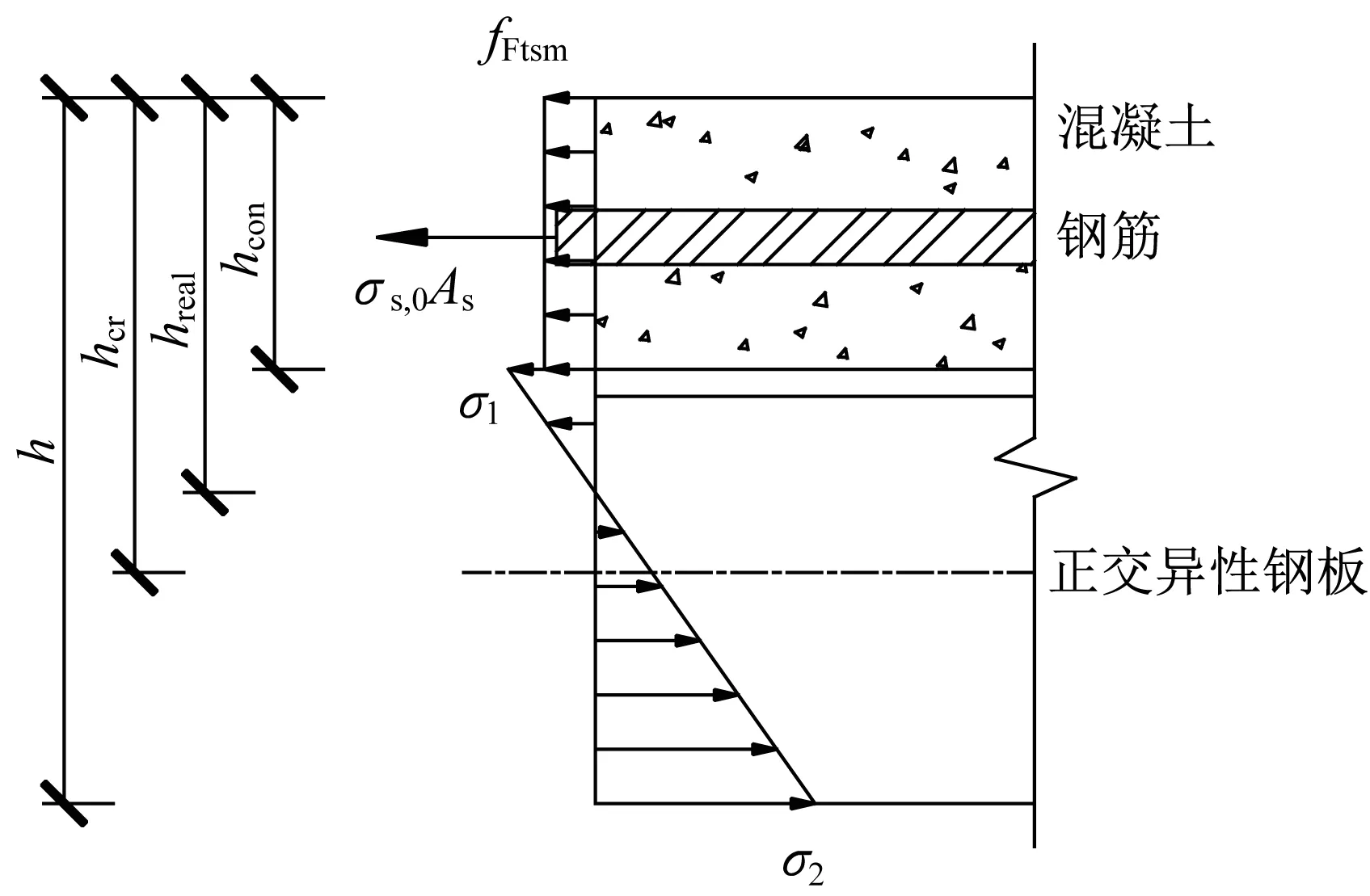
圖1 開裂后斷面的應力分布（不考慮受拉剛化效應）Fig.1 Section stressdistribution afterconcrete crack(Neglecting tension stiffening effect)

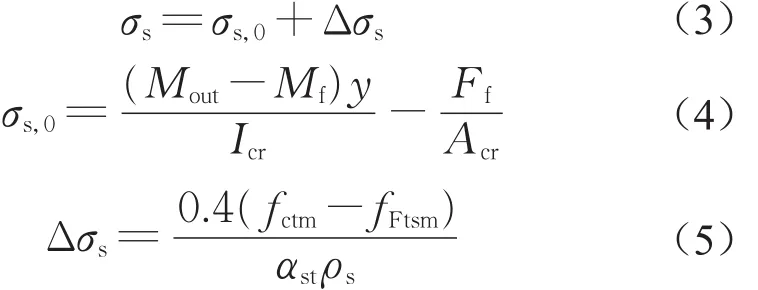
式（4）中，Mf和Ff可以通過圖1所示各內力之間的相互關系得

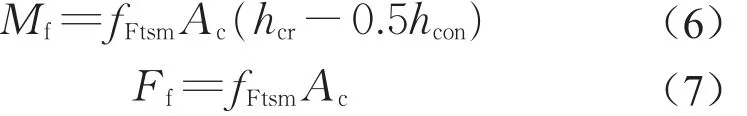
對開裂截面的真實中性軸位置hreal處取矩，得到彎矩平衡方程如下：

斷面軸力合力為0可得到軸力平衡方程如下：

單獨考慮開裂截面，其承受彎矩Mcr和軸力Fcr，導致其中性軸hcr偏移到了整個斷面真實中性軸位置hreal，由此可以計算出開裂斷面自身中性軸位置hcr處的應力 σs，neu為

開裂斷面所承受的軸力Fcr可 表示為

將式（9）—式（11）聯立，得到截面考慮纖維殘余應力影響的實際中性軸位置hreal，如式（12）所示。其中，h為截面高度；hcon為混凝土板厚度，Ac為混凝土板面積；Icr、Acr、hcr分別為開裂截面的慣性矩、面積和中性軸位置。同時需驗證實際中性軸位置是否位于混凝土區域之外，當hreal小于hcon時需迭代計算。

1.3 裂縫間距

歐洲規范2［29］中混凝土裂縫間距可按式（13）計算，考慮了保護層厚度、鋼筋直徑和配筋率的影響。

式中：c為鋼筋保護層厚度，Φ為鋼筋直徑；k1為考慮鋼筋與混凝土黏結性能的系數，帶肋鋼筋取0.8；k2為考慮截面應力分布的系數，對受彎構件取0.5。

對于鋼筋纖維混凝土結構，開裂后纖維作用將降低裂縫間鋼筋與混凝土的應變差，裂縫間距減小［13］。但對纖維混凝土組合橋面板，由于板厚較薄，混凝土裂縫間距不僅受到上述參數的影響，還可能受到橫向鋼筋配置、連接件分布等的影響［30-31］。橫向鋼筋及連接件對混凝土截面的削弱不能忽略。目前較少有文獻探討上述因素之間的相互影響，為了使公式中的參數簡單明確，本文暫時不考慮鋼纖維、橫向鋼筋和剪力連接件的影響，直接引用了歐洲規范4［15］中建議的計算公式。

2 開裂后殘余應力的確定

由前文知，fFtsm是纖維混凝土開裂后裂縫寬度計算的主要影響參數之一。fib模式規范［13］中建議采用缺口梁三點加載試驗確定fFtsm。本文基于已有纖維混凝土受拉本構關系及缺口梁三點加載試驗數據提出一個fFtsm的經驗計算公式。

鋼纖維混凝土開裂后的宏觀和微觀力學行為受到廣泛關注。相關研究可歸結為纖維空間分布研究和單根纖維拔出機理研究等。纖維混凝土開裂后的殘余應力與開裂位置纖維的數量、方向、埋入深度等參數密切相關，它是開裂斷面纖維拔出過程的總和。

2.1 纖維方向與分布影響

Stroeven［16］基于空間幾何概率理論提出了考慮纖維方向和分布影響的纖維混凝土開裂后應力—裂縫寬度計算方法如下：式中：a為纖維特征參數，a=lf/df；Vf為纖維的體積百分率；f為纖維與混凝土之間的摩擦系數；ω2表示由于構件邊界導致的纖維方向趨于受力方向水平面的程度；k為不同纖維的系數，當為平直纖維時k=8，當為帶彎鉤纖維時k=4；w為裂縫寬度；lf為纖維長度。τ*f為纖維自然黏結應力τ1與彎鉤等錨固構造發揮作用時在纖維埋入長度范圍內的等效黏結應力τ'二者之和。其中，根據fib模式規范可知，τ1=與單根纖維拔出機理有關。

2.2 纖維拔出機理

Abdallah［26］指出帶彎鉤纖維如圖 2所示）的拔出過程中會在彎鉤處產生兩個塑性鉸，如圖3所示，所需拉拔力在此時達到最大，可按式（15）計算。隨著纖維繼續拔出，當纖維末端經過第一個彎折位置后，相應塑性鉸消失，所需拔出力降低，隨后兩個塑性鉸均消失。

圖3 纖維拔出過程Fig.3 Fiber pull-out process

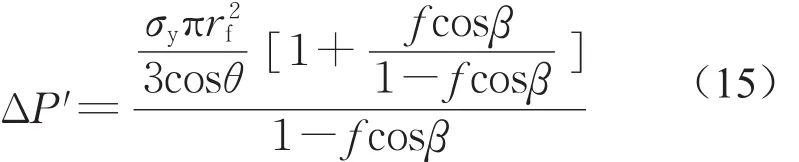
式中：σy為纖維屈服強度；rf為纖維半徑；f為鋼纖維與混凝土之間的摩擦系數；θ如圖2所示，β=（180°-θ）/2。

由此可以得到

將式（15）和式（16）代入式（14）可得

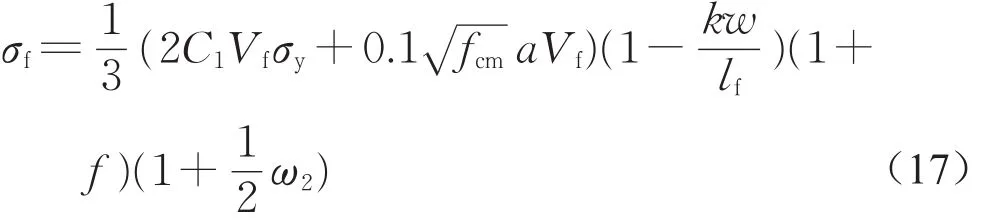
其中：

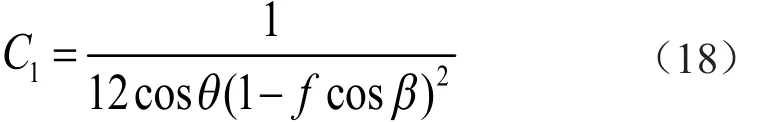
式中：假定纖維各向均勻分布，即ω2=0；纖維混凝土之間的摩擦系數f為定值，目前結構中常用的帶端部彎鉤的鋼纖維，其端部彎鉤形狀相似，即θ、β為定值；考慮缺口梁三點加載試驗中CMOD為0.5mm、摻入纖維為帶2D彎鉤鋼纖維的情況，即σf=fR，1。式（17）可以寫為

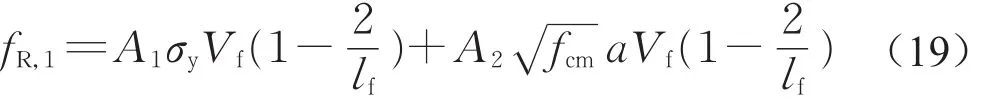
式中：A1和A2為常數。影響fR，1的主要變量為兩個相互耦合的變量：σyV（f1-2/l）f和fcm0.5aV（f1-2/l）f。

將上述兩個變量對35組，如表1所示，文獻中記載的符合EN 14651規定的鋼纖維混凝土三點加載缺口梁試驗數據［32-38］進行線性回歸分析，得到常數A1和A2的取值，分別為：0.084 和 1.180，fR，1預測值的標準差為3.04。因此，有95%保證率的fR，1預測值如下：

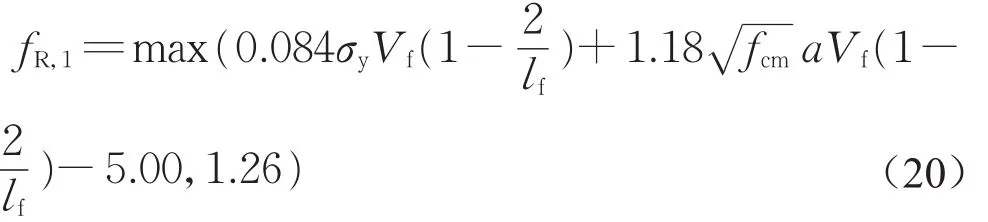
式中：1.26為35組試件中得到的fR，1最小值。

回歸分析的結果如圖4所示。

得到fR，1后即可按式（21）計算正常使用階段驗算中使用的殘余應力值fFtsm［13］。由缺口梁試驗數據計算fR，1的過程中假定了應力沿缺口梁斷面線性分布，而實際的應力分布并非如此，假定正常使用極限狀態下，開裂斷面真實殘余應力沿斷面均勻分布，0.45為真實殘余應力特征值與fR，1之間的轉換系數。

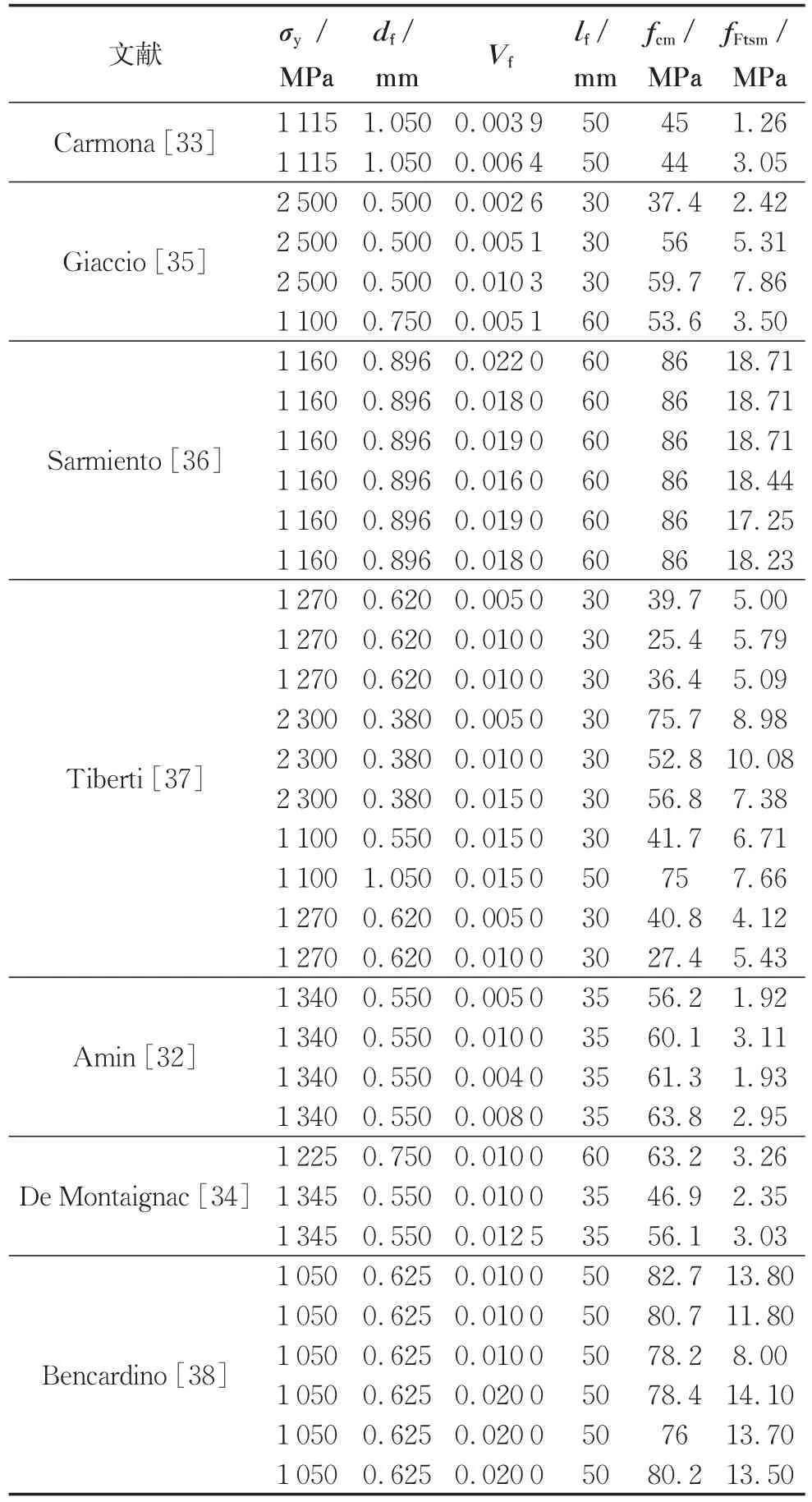
表1 文獻中記載的三點加載缺口梁試驗數據Tab.1 Three-point bending test on notched beam recorded in the literature

圖4 fR，1-pred和fR，1-exp關系曲線Fig.4 fR,1-exp Vs fR,1-pred Curve

系數0.7將正常使用極限狀態殘余應力特征值轉化為均值。

3 試驗驗證

3.1 試驗布置

使用一個纖維混凝土組合橋面板負彎矩加載試驗試件的實測結果對上述裂縫寬度的計算方法進行驗證。試件跨度4m，寬度1.8m，中間設一道橫梁作為負彎矩加載位置，其構造如圖5所示。混凝土采用C80高強混凝土，其28d立方體抗壓強度為113.09MPa，抗拉強度和彈性模量分別為5.3MPa和36 535MPa。采用長度為35mm，直徑為0.55mm帶端部彎鉤的鋼纖維，長徑比64，屈服強度1 100MPa，纖維參量為1%。縱向鋼筋直徑22mm，屈服強度482.2MPa，橫向鋼筋直徑16mm，屈服強度517.5MPa。試件兩端施加豎向約束，通過千斤頂在中間橫梁位置施加荷載，如圖6所示。

3.2 結果對比

根據式（20）～式（21）計算得到此試件正常使用階段驗算采用的殘余應力值：fFtsm=0.45fR，1/0.7=1.18MPa

由式（3）～式（5）可以得到鋼筋應力與裂縫寬度曲線，如圖7所示。圖7中，開裂前鋼筋應力采用未開裂截面的截面特性進行計算。可以看出，開裂前和開裂后的鋼筋應力均與試驗值吻合較好。當荷載達到450kN時，底部U肋發生屈曲，整個斷面剛度降低，導致實測鋼筋應力相對荷載的增幅變大。

裂縫分布如圖8所示。負彎矩最大位置（橫向坐標0）處裂縫間距最大值為390mm，最小裂縫間距為50mm，通過式（13）計算得到的最大裂縫間距為319mm，接近實測的最大裂縫間距。

裂縫寬度方面，如圖9所示，各級荷載下式（2）均給出了與實測值接近但偏安全的估計。針對此橋面板試件在開裂初期給出了較大的裂縫寬度預測值，但在接近極限荷載時實測裂縫寬度與計算值較為接近。同時也可以看出纖維混凝土具有較強的抑制裂縫開展的性能，在結構接近破壞（U肋屈曲）的荷載（590kN）作用下其最大裂縫寬度為0.2mm。

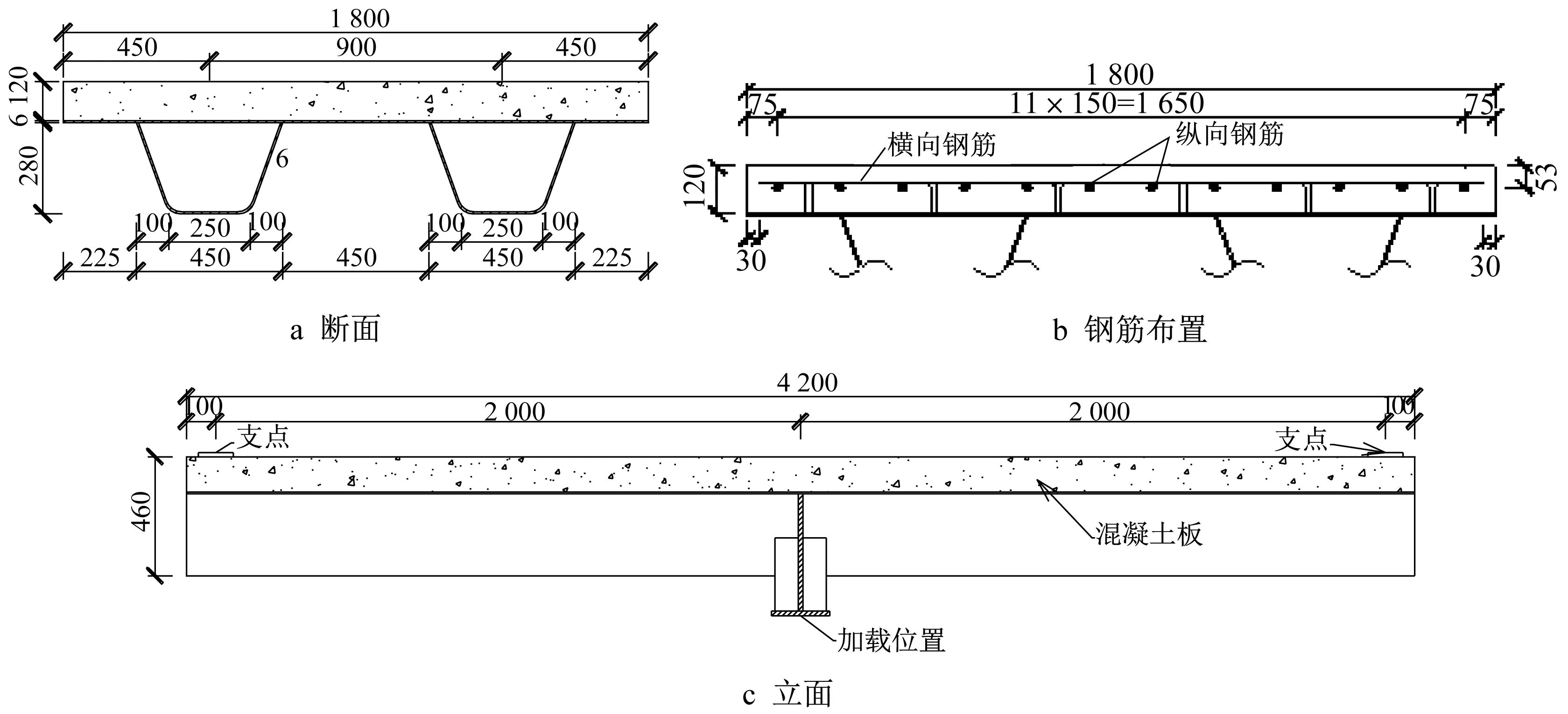
圖5 試件構造（單位：mm）Fig.5 Configuration of Specimen(Unit:mm)

圖6 加載現場Fig.6 Loading site

通過對文獻中記錄的三點加載缺口梁試驗數據進行回歸分析得到具有95%保證率的擬合公式，可以省去試驗確定殘余應力的過程，為設計過程提供了一定的便利。但是目前用于擬合的樣本數據較少。且由于樣本僅僅使用了摻入帶2D彎鉤的鋼纖維的常規混凝土，強度范圍為25.4～86MPa，因此對于摻入直鋼纖維、混雜纖維、合成纖維的混凝土、超高性能混凝土的適用性需要進一步研究。

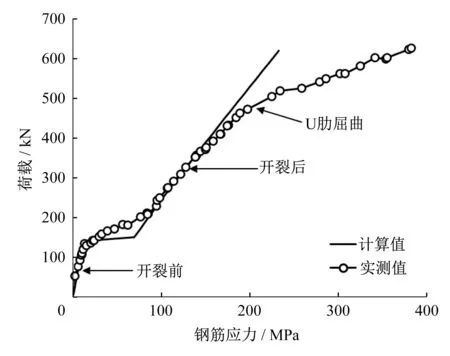
圖7 荷載—鋼筋應力曲線Fig.7 Load—rebar stress curves

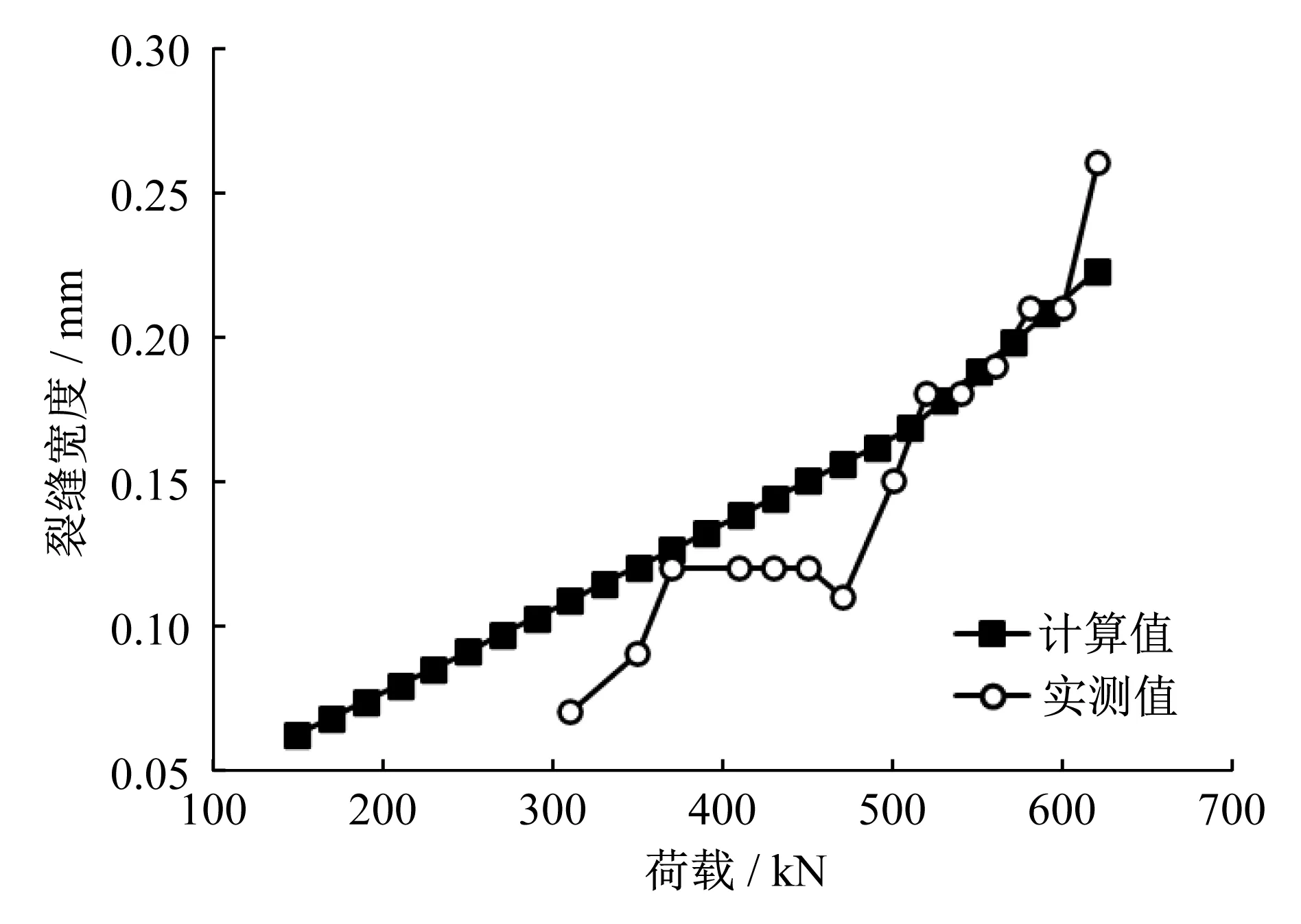
圖9 裂縫寬度—荷載曲線Fig.9 Crack width-load curves

4 結論

提出了一種針對纖維混凝土組合橋面板裂縫寬度預測的計算方法，主要包括殘余應力的理論計算方法和考慮殘余應力有利作用的裂縫寬度預測方法。

（1）提出的纖維混凝土殘余應力計算方法可以根據所采用混凝土的強度等級、纖維的長度、直徑、配置率等參數通過理論計算給出纖維混凝土開裂后的殘余應力，可以用作裂縫寬度驗算。可以省去試驗確定殘余應力的過程。

（2）在歐洲規范4建議的組合結構受負彎矩作用下混凝土層裂縫寬度計算方法的基礎上，考慮纖維混凝土開裂后殘余應力的有利作用，得到了計算纖維混凝土組合橋面板負彎矩區鋼筋應力和裂縫寬度的計算公式。通過與組合橋面板負彎矩加載試驗得到的試驗值進行比較發現，計算得到的鋼筋應力與試驗值吻合較好，計算得到的裂縫寬度與實測值接近且偏于安全。