微型離心泵誘導輪與葉輪軸向距離匹配特性

冷洪飛，姚志峰,2※，湯 遠，王超越，趙浩儒

（1. 中國農業大學水利與土木工程學院，北京 100083；2. 北京市供水網系統安全與節能工程技術研究中心 北京 100083）

0 引 言

微型離心泵因其揚程高，結構緊湊，廣泛應用在國內外航天器的溫控系統流體回路中[1-2]，作為核心動力部件，離心泵的性能直接決定整個流體回路的控溫能力[3-5]，若產生汽蝕，會嚴重威脅航天員和航天器的安全，因此，必須避免離心泵發生汽蝕。為便于后續研究和綜述，這里定義進口直徑小于20 mm的離心泵為微型離心泵。

通常，在葉輪前加裝誘導輪是提高離心泵抗汽蝕性能的重要方法之一[6-7]。然而，在離心泵運行時，液體從誘導輪流出后直接進入主葉輪，由于葉輪進口尺寸固定，誘導輪尺寸往往會受到整體結構上的限制，這便存在誘導輪和主葉輪的匹配問題[8]，導致離心泵不能充分利用誘導輪的高抗汽蝕性能，還可能影響離心泵的運行穩定性。

大量學者通過改進誘導輪的葉片結構[9-11]來提高誘導輪的汽蝕性能和能量特性，但實際上誘導輪與離心泵匹配不合理，也是引起泵效率低下和抗汽蝕性能差的原因之一[12-14]。近年來，一些專家學者針對誘導輪與葉輪的時序位置和軸向距離進行了研究，楊寶峰等[15]對誘導輪與主葉輪時序效應下的流場特性發現，隨誘導輪與主葉輪夾角變化，揚程和效率值變化不大，但當誘導輪葉片位于主葉輪兩葉片中間時，壓力脈動峰值能顯著下降。胡帥[16]研究了誘導輪葉片數對高速離心泵汽蝕工況空泡體積分數影響，發現葉片數為3時，空泡體積分數較少，且誘導輪葉片與主葉輪葉片夾角為48°時，空泡體積分數最少。孫強強等[17]研究發現誘導輪與葉輪的軸向距離對高速離心泵空化性能有較大影響，適當增大軸向距離，可以提高葉輪進口壓力。王文延等[18]研究了高速離心泵匹配性的誘導輪匹配特性發現，葉輪與誘導輪的軸向距離過小會導致離心輪內流動不平穩，并使泵性能下降。盧金玲等[19]則提出離心泵的水力性能隨誘導輪和葉輪間軸向距離的增大而提高。

由以上研究發現，誘導輪與葉輪的交錯角度和軸向距離對離心泵汽蝕性能和能量特性都有重要影響。但交錯角度在實際裝配時不易控制，而誘導輪與主葉輪軸向距離對離心泵性能影響研究尚不深入，且均是針對常規尺寸離心泵內誘導輪的匹配問題進行研究，針對微型離心泵誘導輪與葉輪匹配的特性研究目前尚處于空白。因此，本文以微型離心泵為研究的對象，深入分析誘導輪與葉輪間的軸向距離對離心泵能量特性、汽蝕性能和壓力脈動的影響，并給出量化建議，以期為后續微型離心泵的誘導輪與主葉輪匹配設計提供參考。

1 離心泵幾何模型

本文研究模型為某航天器中應用的屏蔽式離心泵，這種泵型的泵體和電機裝配為一體，內部形成冷卻回路，結構緊湊，且比轉速ns非常小（ns＜60）。離心泵結構示意圖如圖 1所示，主要由泵殼、誘導輪、葉輪和電機 4部分組成。其主要參數為：額定流量Q=0.466 m3/h，設計揚程H=12 m，額定轉速n=11 400 r/min，葉輪葉片數Z1=6，誘導輪葉片數Z2=3，葉輪進口直徑D1=17 mm。

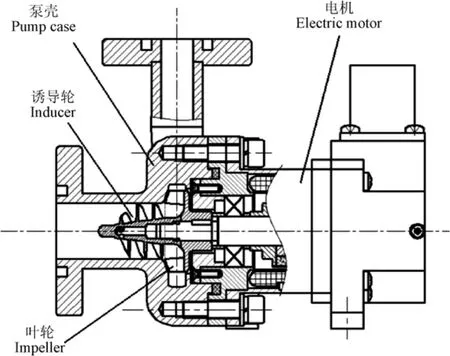
圖1 離心泵結構示意圖Fig.1 Schematic diagram of centrifugal pump

2 數值計算模型

2.1 網格劃分

離心泵計算域采用六面體結構化網格和四面體非結構化網格組合的混合網格劃分策略。因葉輪為圓柱型葉片，比較規則，故文中針對葉輪和進出口延伸段均使用六面體網格，誘導輪和蝸殼部分因結構復雜，使用非結構四面體網格。其中葉輪的計算域網格示意圖如圖 2所示。

圖2 葉輪網格劃分示意圖Fig.2 Meshing diagram of impeller

采用基于理查德森外推法的網格收斂準則[20-21]進行網格無關性判定。該方法按比例繪制 3套網格，在最精細的網格方案基礎上，推算繼續增加網格數目對某項流場參數的預測結果，若滿足收斂標準，判定 3套網格中數目最多的一套方案滿足計算需求，若不滿足收斂準則，則需進一步加密網格或重新調整網格的整體數目。本文選取的3組網格單元數量如表1所示。在額定工況下，以離心泵出口截面的平均壓力(Pout)進行網格誤差預估，第 3組網格計算結果的網格收斂指數（Grid Converge Index, GCI）GCI=0.36%，滿足使用精度要求。

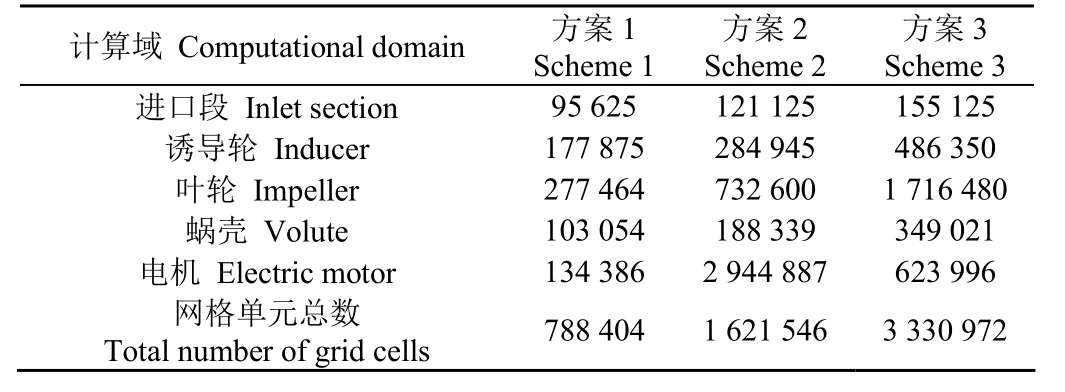
表1 計算域網格單元數Table 1 Grid cell numbers of calculation domain

近壁區采用標準壁面函數進行求解，需通過控制無量綱參數y+的取值范圍以保證壁面網格尺度滿足表面流體單元的流速分布規律接近對數律[22]分布形式。對于采用標準壁面函數的湍流數值計算，y+建議范圍為 0～300[23]。圖3為誘導輪和葉輪葉片表面y+分布情況，均符合壁面函數使用要求。

壓電體的表面電極上所產生的電荷量與很多因素有關，D33工作模式的壓電陶瓷兩端的電壓幅值V的理論計算公式如下[14]：

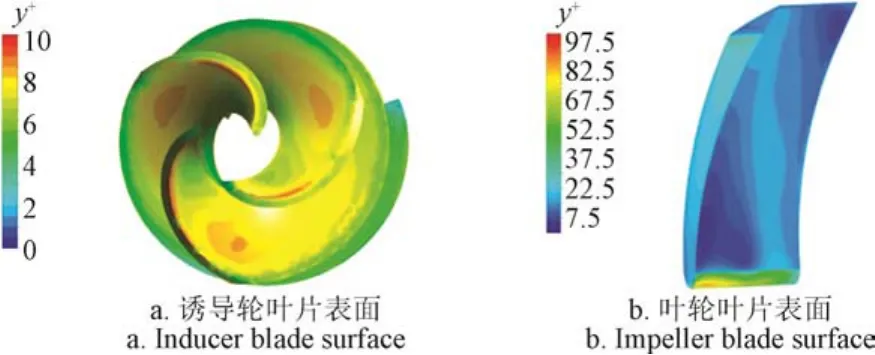
圖3 葉片表面無量綱參數y+的分布情況Fig.3 Distribution of dimensionless parameter y+ on blade surface

2.2 數值方法

數值計算采用CFX軟件，分別選用適用于旋轉機械流動計算的SSTk-ω湍流模型[24-25]和Zwart空化模型[26]，固體壁面采用無滑移、絕熱邊界條件，定常計算時動靜交界面設置采用Frozen Rotor模式處理；非定常計算的動靜交界面設置采用Transient Rotor Stator 模式處理[27]。壓力-速度耦合采用SIMPLEC[28-29]算法；差分格式采用二階迎風格式；工作介質為水，汽蝕計算時，工作介質為25 ℃水和水蒸汽，通過調節進口壓力來控制離心泵內空化發展情況。非定常計算時，根據普朗特數（Courants）準則和非定常計算的周期性時間尺度原則[30]，選取時間步長為4.386e-5s，為葉輪葉片旋轉周期的1/120，計算16個旋轉周期，選取最后4個周期進行壓力脈動分析。

基于上述方法，用第 3組網格進行離心泵流場的數值計算，并在北京航天動力研究所小流量液流試驗臺進行了水力試驗。數值計算結果及水力試驗結果如圖 4所示，在額定流量點，揚程誤差為0.3%，數值計算結果較為準確，可用于不同軸向距離下的能量特性、汽蝕特性和壓力脈動特性分析。

圖4 計算準確性驗證Fig.4 Verification of calculation accuracy

3 軸向距離對離心泵性能影響

為了分析誘導輪與葉輪間的軸向距離對離心泵性能的影響，定義誘導輪名義長度為S(mm)，用式（1）表示：

式中Ly為誘導輪葉片進口邊至出口邊的軸向尺寸，mm；ty為誘導輪的葉柵稠密度。本文中誘導輪葉柵稠密度設計值為ty=2，軸向長度Ly=14.8 mm，針對本文研究對象，定義軸向距離為誘導輪出口邊至葉輪進口邊的軸向尺寸（l，mm），選取0.1S，0.5S、1.0S、1.5S和2.0S共5種軸向距離進行離心泵性能對比分析。

3.1 軸向距離對離心泵能量特性影響

圖 5給出了額定工況下揚程和效率隨軸向距離增加的變化曲線圖。可以看出，隨軸向距離增加，揚程曲線和效率曲線變化趨勢基本一致。當軸向距離由0.1S增大到1.0S，揚程和效率逐漸增加，且1.0S和1.5S的揚程和效率基本一致，但軸向距離繼續增大到2.0S時，揚程有所下降，而效率變化很小。與0.1S相比，軸向距離增加至1.0S時，揚程提高了0.61 m，達到最大13.30 m，效率提高了5.8%，達到最大值49.50%，性能得到較大提升。但軸向距離繼續增加，揚程和效率均不再繼續提高。

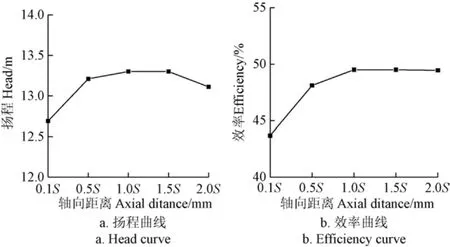
圖5 外特性曲線Fig.5 External characteristics curve

圖6為額定工況下，葉輪中間截面的渦量分布云圖，可以看到，l=1.5S時，強旋渦分布最少。軸向距離增加至0.5S時，葉輪進口處的弱旋渦（渦強在0～1 000/s范圍）基本消失，但進口邊的強旋轉渦（5 000～7 000/s）仍然存在，當軸向距離增加至1.0S和1.5S時，旋渦強度明顯減弱，渦強均在3 000/s以下，分布面積也明顯減少；而軸向距離繼續增加至2.0S時，渦強增大，進口的弱旋渦和出口的強旋渦均顯著增多，這種現象與揚程曲線相對應，分析是導致水力損失增加的主要原因。

整體來看，隨軸向距離增加，誘導輪出口流場能夠擴散更加充分，因此葉輪進口處流態得到改善，減少了流動損失，進而增大離心泵的揚程并提高效率。但軸向距離增大至2.0S后，流道過長，且流速增大，能量損失增多，導致揚程小幅降低。

圖6 不同軸向距離l的葉輪中間截面渦量分布圖Fig.6 Vorticity distribution of the middle section of impeller for different axial distance l

3.2 軸向距離對離心泵汽蝕性能影響

圖7為離心泵額定流量下，5種軸向距離下的離心泵汽蝕余量曲線。可以看出，軸向距離l=0.1S時，臨界汽蝕余量NPSHc=1.6，軸向距離增加至l=1.0S時，NPSHc=1.2 m，降低了0.4 m，但軸向距離繼續增加后，臨界汽蝕余量（與無汽蝕的揚程相比，揚程下降3%時的汽蝕余量為臨界汽蝕余量）不再降低。

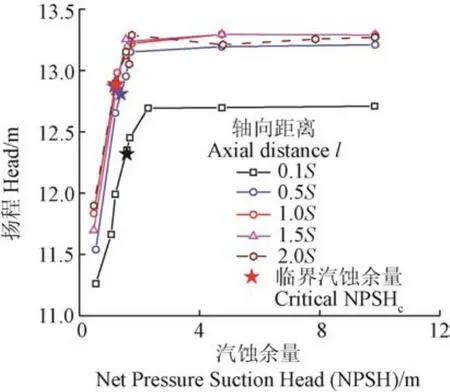
圖7 NPSH曲線對比圖Fig.7 Comparison chart of NPSH curve

圖8 不同NPSH下誘導輪內空泡體積分數等值面圖（空泡體積分數Vf =10%）Fig.8 Isosurface of cavity volume fraction in inducer at different NPSH (Cavity volume fraction Vf =10%)

比較5種軸向距離的離心泵在2種汽蝕工況下的空泡體積分布圖可以看出，與l=0.1S相比，軸向距離增加后，誘導輪內的空泡均顯著減少，但l＞1.0S時，空泡體積不再繼續減少。分析是因為隨軸向距離增加，誘導輪出口處流動可以充分發展擴散，進而提高了誘導輪內部壓力，使誘導輪內空泡減少。但誘導輪內壓力不會無限升高，故軸向距離繼續增大后，泵內汽蝕性能不會繼續改善，因此，在軸向距離l=1.0S時，誘導輪即可達到較好的改善離心泵汽蝕性能的目的。

3.3 軸向距離對前置誘導輪離心泵壓力脈動影響

圖 9為計算域中的壓力脈動的測點布置圖，分別在誘導輪軸向截面內，葉輪及其前間隙的軸向截面，蝸殼中截面內布置了11個監測點。由前期研究可知，前置誘導輪離心泵中，誘導輪中間，葉輪前間隙靠近進口邊處，葉輪出口處和隔舌處是各計算域壓力脈動幅值較大的位置，且誘導輪對葉輪的壓力脈動影響較大，因此，本節以其中5個監測點P2，P4，P5，P7，P9為例，分析額定工況下3種軸向距離時的壓力脈動特性。

采用無量綱壓力系數Cp表示離心泵壓力脈動，計算公式如式（2）所示。

式中 ΔP為監測點壓力與其監測周期內的平均壓力值的差，Pa；ρ為流體密度，kg/m3，u2為葉輪出口的圓周速度，m/s。

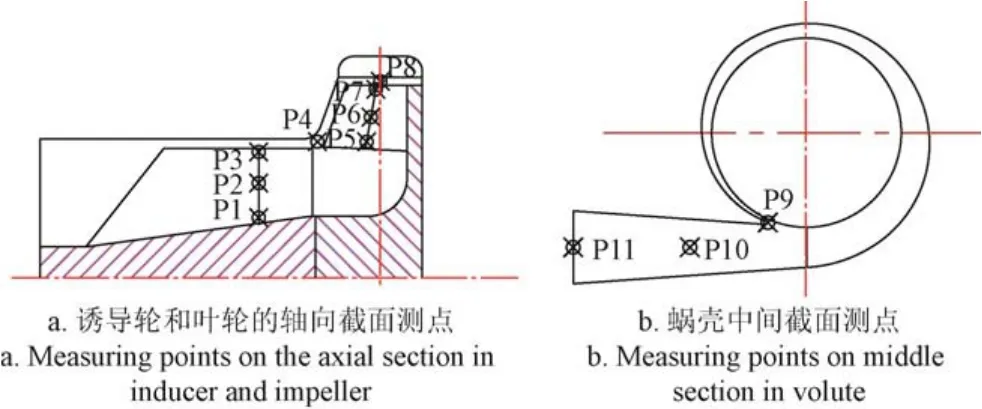
圖9 壓力脈動測點布置圖Fig.9 Layout of pressure pulsation measuring points

表 2為各監測段監測點的壓力系數脈動幅值（后文簡稱壓力脈動幅值），可以看出，P2點和P9點壓力脈動幅值隨軸向距離增加逐漸降低，并分別在軸向距離l=1.5S和l=1.0S時降至最低；P4、P5和P7點的壓力脈動幅值均隨軸向距離增加而升高，其中，P5點在l=2.0S時增幅最大，達到45.40%；P7點的壓力脈動幅值最小，但隨軸向距離增加，該點幅值在l=1.5S增加到最高值時，增幅僅1.97%，變化較小。結果表明，軸向距離增加會使離心泵葉輪進口附近的壓力脈動幅值增大，但對泵內壓力脈動幅值最大值的影響較小。

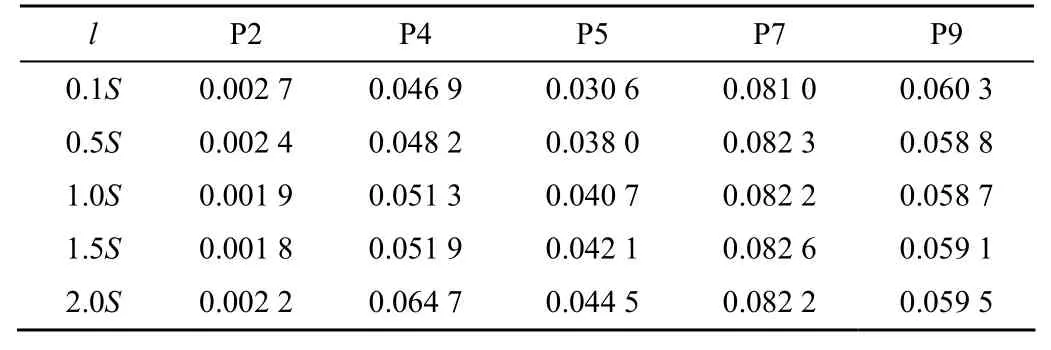
表2 不同軸向距離下各監測點的壓力脈動幅值Table 2 Pressure pulsation amplitude value of each monitoring point at different axial distances

圖10為各測點的壓力脈動頻域圖。P2點和P4點在軸向距離為0.1S時，除葉輪倍頻（1 140 Hz）外，還存在誘導輪倍頻（570 Hz）的諧頻，隨軸向距離增加，諧頻幅值減小，對距離誘導輪較遠的P9點，在l=0.5S時，諧頻消失。說明對于固定計算域，軸向距離較小時，會受到誘導輪旋轉的影響而產生較小幅值的諧頻，軸向距離增加后，誘導輪的旋轉對下游的壓力脈動影響減弱，諧頻消失。對于葉輪內的P5點和P7點，因諧頻較多，且誘導輪產生的諧頻幅值較小，故沒有觀測到明顯的誘導輪倍頻。

3.4 壓力脈動變化機理分析

為進一步分析瞬態流場下的流動特性以探索因軸向距離增加引起的壓力脈動變化機理，本文選取渦旋識別的Omega準則[31]對葉輪中間截面進行渦動特性分析，其識別參數R的定義為

式中||Ω||F和||D||F為旋轉率張量和應變率張量的F-范數，ε為一正小量以保證分母不為0。可以看出R的取值范圍為[0，1]，當R=0時，表示流場無旋轉運動，當R=1時，表示流場為純旋轉運動。本文規定R≥0.5時，流體流動處于“強渦動”狀態，此時流動微團的渦量占據主導作用，可以認為此時存在旋渦結構；當R＜0.5時，處于變形量占優狀態，認為流體微團的流動處于“弱渦動”狀態。

由于軸向距離增至1.0S后，脈動幅值和頻率變化較小，因此，僅針對l=0.1S，l=1.0.5S，l=1.0S的軸向距離，以額定工況下的葉輪中間截面流場為例進行瞬態流動的分析。這里選取一個旋轉周期（1/190 s）的平均4個時刻，起點記為0 s，圖11為不同時刻下葉輪中間截面的Omega分布圖。可以看出，在不同時刻，3種軸向間距下的葉輪中間截面的Omega分布均出現“交替渦動”現象，即在“強渦動”條件下（1/760和3/760 s時刻），靠近輪轂的區域出現了大片環形強旋轉區域，而在“弱渦動”條件下（0和1/380 s時刻），靠近輪轂的區域未出現如前述的環形強旋轉區域。但不同時刻下，隨軸向距離增加，葉道內均會出現彌散的強旋轉區域。

圖10 壓力脈動頻域圖Fig.10 Frequency domain of pressure pulsation

圖11 葉輪中間截面Omega 分布Fig.11 Omega distribution of the middle section of impeller

整體來看，軸向距離增大后，在靠近輪轂側，強渦動時刻的渦旋有所減弱，弱渦動時刻的渦旋有所增強；而葉道內彌散的強渦旋在任一時刻均有所增多，這與泵內相應位置監測點壓力脈動變化情況相似，即靠近誘導輪的監測點壓力脈動幅值隨軸向距離增加而降低，葉輪內監測點隨軸向距離增加而升高。推測Omega分布與離心泵壓力脈動有一定的聯系，初步分析是軸向距離增大后，葉輪受誘導輪影響產生的旋轉效應減小，但壓力脈動幅值升高。

4 結 論

本文采用數值方法，分別對軸向距離為l=0.1S，0.5S、1.0S、1.5S和2.0S（S為誘導輪軸向長度與葉柵稠密度的比值）的前置誘導輪離心泵進行能量特性和流場特性的分析。得到以下主要結論：

1）隨軸向距離增加，離心泵在額定工況下的揚程和效率均有所增加，其中，軸向距離為1.0S時，揚程增加到最大值13.30 m，效率增加到最大值為49.50%，軸向距離繼續增大后，揚程和效率會有所降低。與軸向距離為0.1S相比，l=1.0S時，揚程增加了0.61 m，效率增加了5.8%。

2）軸向距離增加至 1.0S時，臨界汽蝕余量下降約0.4 m，空泡分布明顯減少，但增至l=1.5S后，臨界汽蝕余量不會繼續降低，離心泵汽蝕性能未能繼續改善。

3）隨軸向距離增加，誘導輪和隔舌處監測點壓力脈動幅值逐漸降低，葉輪內監測點脈動幅值逐漸增大，且葉輪進口處脈動幅值變化最大，在l=2.0S時，增幅達到45.4%，但泵內壓力脈動幅值最大的葉輪出口處的增幅較小，僅增加1.97%。

綜上分析，軸向距離為0.1S時，會影響誘導輪的抗汽蝕效果。在額定工況下，當軸向距離增大到1.0S時，揚程和效率均顯著提升，且汽蝕余量降低；繼續增大后，整體性能改善不大。但是隨軸向距離增加，葉輪前間隙及內部監測點的壓力脈動幅值會增大，因此，綜合考慮誘導輪與葉輪軸向距離對泵外特性，汽蝕特性和壓力脈動的影響，建議選取軸向距離l=1.0S，此時能使誘導輪與葉輪的流動匹配達到最佳，有利于離心泵穩定運行。