兩輪差速移動機器人系統誤差調校研究

劉懷民,王湘江

(南華大學資源環境與安全工程學院，湖南 衡陽 421001)

0 引言

移動機器人自主導航過程中，需要對機器人自身在工作環境中的位置進行精確估計。移動機器人位置誤差分為系統誤差和非系統誤差[1-2]。系統誤差來源包括不相等的車輪直徑、車輪軸距的不確定性和運動學建模誤差等因素。這類誤差由于機器人設計不合理及精度不夠等因素導致，屬于移動機器人的固有屬性，與機器人導航的外界環境無關，且在機器人導航過程中通常不會發生改變。而非系統誤差則是由環境條件導致，具有隨機屬性。例如地面不平整、地面上的小物體及車輪打滑等[3-4]。非系統誤差的不確定性可以通過使用外部傳感器獲得的絕對位置信息來建模。

國內外學者針對移動機器人系統誤差進行深入研究，提出了多種有效的調校方法。Borenstein和Feng[4]提出UMBmark校核方法。該方法通過機器人雙向正方形路徑試驗獲得系統誤差調校參數。Maldonado-Bascón等[5]提出了一種比較簡便的差動驅動機器人標定方法。該校準過程可在線完成，縮減記錄機器人位置的時間。相比UMBmark方法，差動驅動機器人標定方法可減小調校測試場地空間。Jihoon Seong等[6]提出了一種適用于車型移動機器人的里程計校準方法。該方法僅需測量機器人沿軌跡運行后的航向誤差，便可對移動機器人進行了標定，從而有效消除近似誤差、減小標定誤差。Baeksuk Chu等[7]針對全向移動機器人提出了一種位置補償算法。該算法利用超音波距離感測器測量機器人位置和方向信息，無需任何復雜的路徑規劃，便可減小移動機器人位置偏差。Kuisong Zheng等[8]針對服務機器人提出了一種通用批量標定框架。該方法將運動捕捉系統作為虛擬的外部測量裝置，提供實時、準確的運動數據，便于被測機器人的里程計標定。而國內研究者主要針對移動機器人系統誤差模型和調校方法驗證開展了研究。其中，貝旭穎等[9]根據Umbmark方法的不足考慮系統誤差的耦合效應，提出了一種新的擴展誤差校正方法。張勝賓等[10]利用Pioneer3-AT差動輪式移動機器人，進行了UMBmark校核驗證性試驗，驗證了UMBmark 校核方法在提高移動機器人自主定位精度方面的有效性。達興鵬等[11]基于拓展卡爾曼濾波算法，提出了一種機器人里程計系統誤差及激光雷達安裝誤差迭代標定方法。

本文針對輪式差動驅動機器人[12]，提出了一種簡單、有效的校準兩輪差速移動機器人系統誤差的方法。通過機器人的位置偏差數據獲得校準參數，并采用直線往返路徑和雙方形封閉環路徑試驗，對該系統誤差校準方法的有效性進行驗證。

1 移動機器人運動學模型

兩輪差速驅動移動機器人可轉化為一個移動關節和一個旋轉關節。移動關節運動方向是移動機器人向前運動的方向。兩輪差速移動機器人運動學簡化模型如圖1所示。

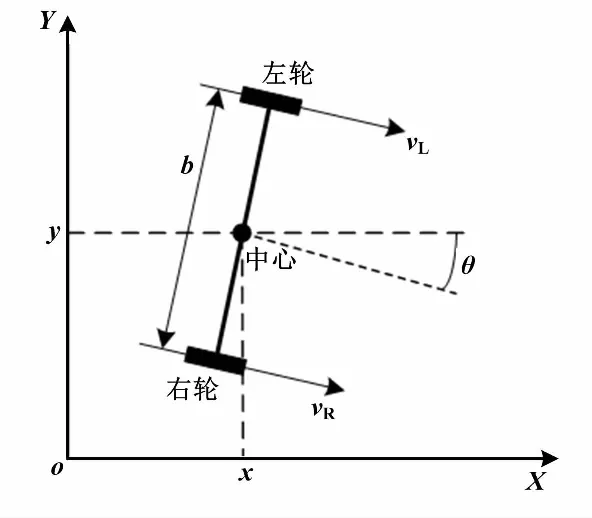
圖1 兩輪差速移動機器人運動學簡化模型

移動機器人的左右兩個電機分別獨立驅動，質心在底盤中軸線上的兩輪中點處。因此，移動機器人的運動學模型可以簡化為簡單的幾何運動問題。

根據移動機器人的運動模型，對兩輪差速驅動移動機器人的當前位置進行估計。其關系式如下：

(1)

(2)

式中：vL為左輪的線速度;vR為右輪的線速度；ωL為左輪的角速度;ωR為右輪的角速度；v為機器人的線速度；ω為機器人角速度；b為軸距；R為輪子的半徑。

設移動機器人在二維坐標系中的坐標為(x,y)、移動機器人的運行方向與x軸之間的夾角θ，就可用向量(x,y,θ)表示移動機器人的位置姿態。其運動方程為：

(3)

結合式(1)與式(2)，可獲得移動機器人姿態方程：

(4)

2 系統誤差調校方法

兩輪差速驅動移動機器人的主要系統誤差來源是“車輪直徑不相等”、“車輪有效軸距不確定”以及“車輪直徑的實際平均值與標稱平均值不相等”三個因素。機器人左右兩輪直徑不等引起的誤差定義為輪徑誤差Ed。機器人車輪有效軸距不確定導致的誤差定義為軸距誤差Eb。機器人兩輪子直徑的實際平均值與標稱平均值不相等產生的誤差定義為比例誤差Es。Ed僅對機器人的直線運動造成影響，Eb僅對機器人的旋轉運動造成影響，而Es同時影響機器人的直線運動和旋轉運動。

(5)

(6)

(7)

以上公式中：Dl為左輪的實際直徑;Dr為右輪的實際直徑；ba為機器人實際輪距;bn為標稱輪距；Da為兩輪子直徑的實際平均值;Dn為機器人和標稱平均值。

系統誤差會導致機器人在直線路徑的終點產生轉向角。機器人行進軌跡與位置偏差示意如圖2所示。

圖2 機器人行進軌跡與位置偏差示意圖

機器人沿坐標系中的X軸直線移動為路徑D。該路徑軌跡為機器期望軌跡。受Ed與Es因素的影響機器人的實際行進軌跡會偏離路徑D，其實際路徑為A。機器人實際行進軌跡終點在X和Y軸方向上的測量偏差值通過式(8)獲得：

(8)

式中：n為試驗測試的次數；Δxi和Δyi分別為每次試驗在X和Y軸方向上的偏差。

移動機器人行進到指定距離，輪子旋轉次數為N。機器人以標稱值Dn為參數編程直線行進，則機器人直線行進的期望軌跡長度D與實際行進軌跡A長度分別為N×π×Dn和N×π×Da。當β=0時,Δy=0,機器人將沿著X軸坐標直線行進，坐標軸Y方向無偏差。則：

(9)

(10)

機器人實際軌跡曲率半徑幾何關系如圖3所示。

圖3 機器人實際軌跡曲率半徑幾何關系圖

機器人實際軌跡曲率半徑R可通過圖3中的三角幾何關系獲得:

(11)

(12)

根據式(11)所獲得的移動機器人實際軌跡曲率半徑R，導致機器人產生彎曲路徑的左右輪直徑之間的比率Ed可根據式(12)獲得[5]。由于輪徑偏差導致移動機器人實際路徑為曲線，其實際路徑的曲率半徑R與輪徑偏差示意如圖4所示。

圖4 實際軌跡曲率半徑R與輪徑偏差示意圖

圖5 機器人定點順/逆時針往返示意圖

假定移動機器人旋轉指定角度輪子旋轉次數為M，由于Eb影響，機器人旋轉時的實際轉角值與期望值π存在偏差，其偏差角為θ。根據三角幾何定理，可知：

(13)

(14)

式中：θ為矢量角度。

通過上述方法獲得機器人輪徑誤差Ed、軸距誤差Eb和比例誤差Es后，根據平均輪徑的定義可知：

(15)

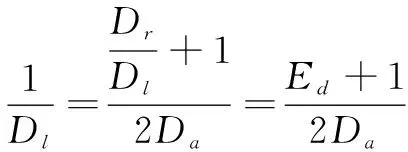
(16)

由式(15)～式(16)可得:

(17)

(18)

將式(15)～式(18)代入式(4)，可獲得具有調校參數的雙輪差速移動機器人運動學方程：

(19)

調校參數Es、Ed與Eb確定后，可通過修改機器人微控制器的運動學算法代碼進行系統誤差補償。

3 試驗驗證與結果分析

試驗裝置如圖6所示。

圖6 試驗裝置

機器人的參數配置為：輪徑d=180 mm；軸距b=278 mm；編碼器分辨率P=1 200 P/R。考慮到機器人車輪建模誤差的正常范圍隨車輪特性和環境而變化，試驗中使用的機器人輪徑誤差限制在±1.0%范圍內。通過機器人試驗軌跡(位置和方向)變量，獲取機器人系統誤差校準參數試驗。首先，通過編程使機器人直線行走指定距離D,根據機器人起始點位置坐標與轉向角獲得校準參數Es、Ed；然后機器人進行定點轉向返回起點，獲取校準參數Ed。其中，定點轉向第一次順時針方向旋轉角度為π，第二次逆時針方向旋轉角度為π。為了有效減小隨機干擾，反映機器人系統誤差情況，機器人直線行走過程中將機器人左右驅動輪角速度值設為相等，而在定向轉向過程中左右輪的角速度值大小相等、方向相反。

圖1給出了GaAs晶體體內橢圓主軸y”指向隨太赫茲頻率的變化.從圖1可以看出，橢圓主軸y”和z”指向隨太赫茲波的頻率變化趨勢不同.當f(0.1 Thz,1.1 Thz)范圍內時，z”軸指向與y”指向恰好相反.當f(1.1Thz，3.2 Thz)時，z”軸指向與y”指向隨太赫茲波的頻率增大而出現周期性的變化.其變化趨勢與三角函數Tan函數類似.

為了驗證試驗過程中機器直線行進距離和速度與比例誤差Es的關系，編程使機器人直線行走指定距離D為2～10 m、速度V為0～2 m/s。比例誤差Es與軌跡距離關系如7所示。

圖7 比例誤差Es與軌跡距離關系圖

比例誤差Es與行進速度關系如圖8所示。

由圖7與圖8可知，移動機器人比例誤差Es為固定值，由Es引起的偏差屬于機器人的固有屬性與機器人直線行進的距離無關。但隨著機器人速度遞增，比例誤差Es存在遞增趨勢，但變化幅值范圍較小，變化范圍在0.947 2～0.968 8之間。試驗過程中，為防止輪子出現打滑的情況影響校準參數獲取，機器人在行進過程中應保持較低速度，以減小輪子打滑等非系統誤差因素對試驗結果的干擾。考慮到試驗場地的限制，機器人直行軌跡指定距離D取4 m，線速度設定為V=0.25 m/s，角速度設為ω=0.785 rad/s。機器人參數設置如表1所示。

圖8 比例誤差Es與行進速度關系圖

表1 機器人參數設置

每組試驗重復10次，并根據機器人相應的期望目標點測量其位置偏差。圖9為調校前機器人直線行進終點位置分布。

圖9 調校前機器人直線行進終點位置分布圖

將試驗所測機器人位置偏差結果代入式(8)～式(12),計算可得Es=0.947 6、Ed=1.003。機器人逆/順時針轉向π返回點位置分布如圖10所示。

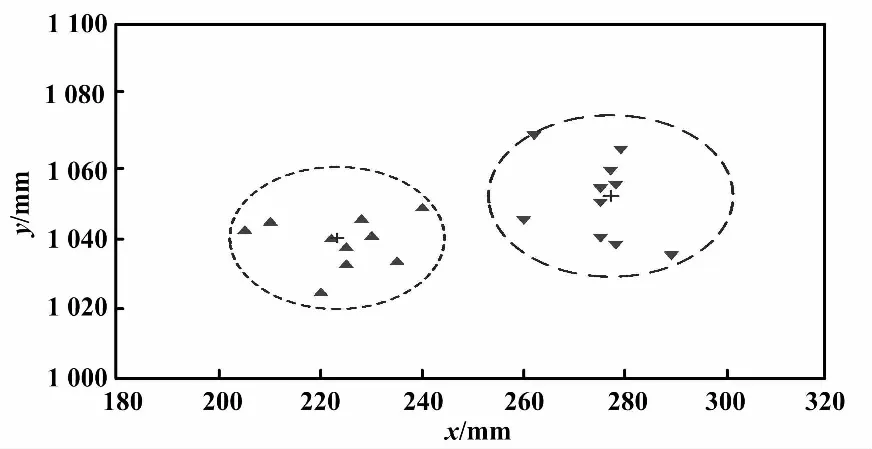
圖10 機器人逆/順時針轉向π返回點位置分布圖

將位置偏差結果代入式(13)、式(14)，計算可得偏差角θ=0.501 8、Eb= 1.190 1。 將上述通過試驗數據計算所得調校參數Es=0.947 6、Ed=1.00 3、Eb=0.947 6代入式(19)中，修改機器人算法代碼后重復上述試驗步驟，獲得的機器人調校前后位置偏差如圖11所示。

圖11 機器人調校前后位置偏差

通過雙方形封閉環路徑試驗，進一步對比機器人調校前后位置偏差改善情況。雙方形封閉環路徑如圖12所示。

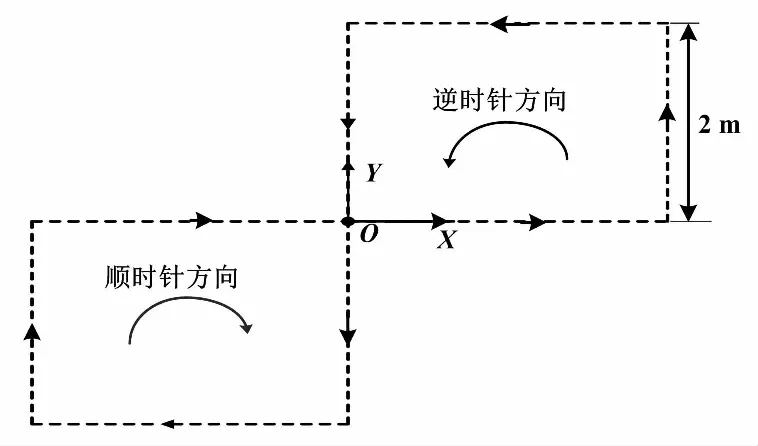
圖12 雙方形封閉環路徑

機器人從起點O出發，經不同的方形封閉環后回到起點O。圖13為機器人的調校前后位置偏差。

圖13 調校前后位置偏差

為了定量反映調校前后機器位置偏差的改善情況，采用偏差系數δr與偏差改善系數δm進行評估。偏差系數δr與偏差改善系數δm定義如下：

(20)

(21)

式中：δmb和δma分別為校準前后偏差系數的平均值。

機器人位置偏差正態分布如圖14所示。

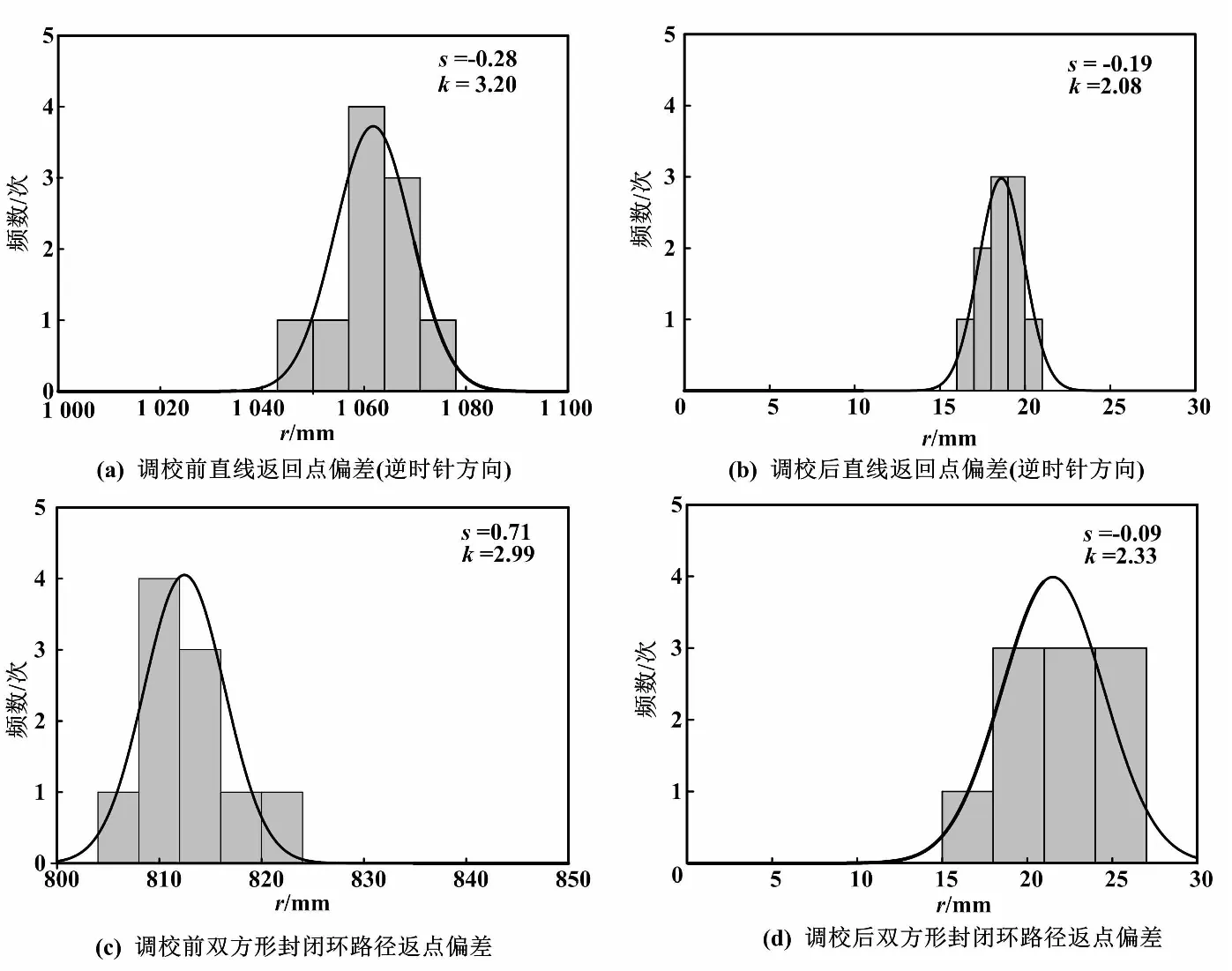
圖14 機器人位置偏差正態分布圖

正態分布圖可清晰地反映機器人試驗的次數、位置偏差平均值、標準偏差，每組統計值計算采用10個樣本(n=10)。表2為機器人調校試驗數據指標，即校準前后根據試驗數據確定的機器人位置的平均誤差值、傾斜度(s)、峰度(k)和標準偏差(σ)估計值。

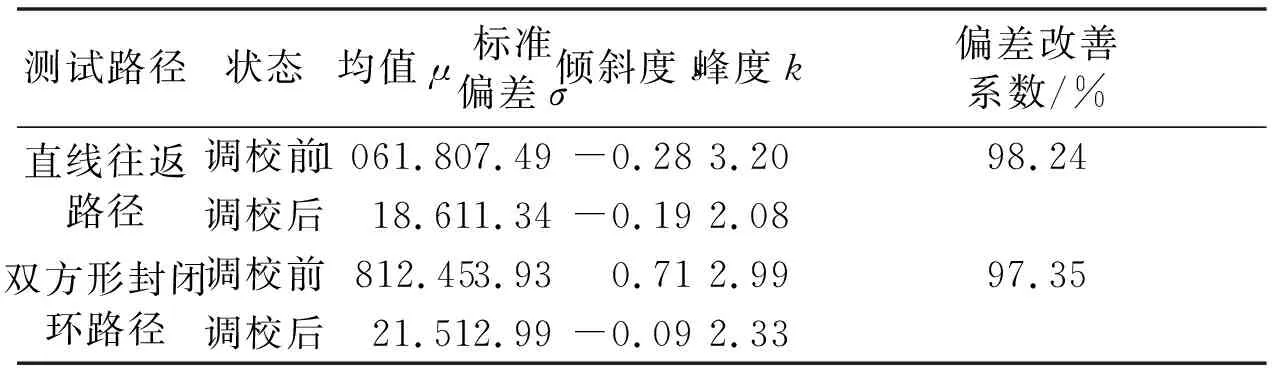
表2 機器人調校試驗數據指標

由圖14和表2可知，移動機器人經調校參數校正后機器的位置偏差明顯改善。采用直線往返路徑，位置偏差結果改善98.24%，采用雙方形封閉環路徑，位置偏差結果改善97.35%。由圖14分析可知，調校參數Eb對機器人偏差影響最大。其主要通過機器人轉向時產生較大的偏差角，從而影響機器人的位置精度。

4 結論

本文提出了一種簡單、有效的測量與校準兩輪差速移動機器人系統誤差的方法。該校準方法通過機器人指定距離的往返移動所產生的位置偏差數據，獲得校準參數Es、Ed和Eb。通過實施直線往返路徑和雙方形封閉環路徑試驗，評估調校參數的有效性。試驗結果表明：調校后機器人的位置偏差改善程度分別達98.24%和97.35%。同時，本文提出的校準方法采用直線往返調校路徑，能夠較大程度地減少調校場地的尺寸。后續的研究工作可考慮驗證該方法在線調校的實用性，以便進一步提高移動機器人的定位精度。