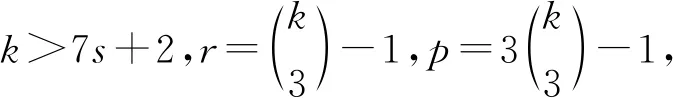樹的D(r)-點可區別邊染色

李澤鵬， 耿培倫, 陳祥恩

(1.蘭州大學 信息科學與工程學院， 甘肅 蘭州 730000; 2.西北師范大學 數學與統計學院, 甘肅 蘭州 730070)

0 引 言

圖的可區別染色是近年來圖染色研究的熱點問題，主要體現圖的局部結構顏色集合之間的可區別性.圖的點可區別正常邊染色是Burris在其博士論文中首次提出的[1]，此后該問題也被稱為強邊染色[2].圖G的點可區別正常邊染色是指G的一個正常邊染色，使得任意兩個頂點的色集合不同.使得G有k-點可區別正常邊染色的最小正整數k稱為G的點可區別正常邊色數，記為′v(G).

Zhang等[3]將任意兩點可區別的條件放松為任意兩個相鄰頂點可區別，從而提出了鄰點可區別正常邊染色的概念(也稱為鄰強邊染色).圖G的鄰點可區別邊色數是指對G進行鄰點可區別邊染色所需要的最小色數，記為′a(G).通過分析一些特殊圖類，如樹、圈、完全二部圖和完全圖等的鄰點可區別正常邊色數，學者們提出了下面的猜想.

猜想1對任意連通圖G(|V(G)|≥6), 有

′a(G)≤Δ(G)+2.

對于更一般的情況，張忠輔等[4]在2006年提出了圖的距離不大于r的任意兩點可區別的正常邊染色，即D(r)-點可區別正常邊染色.顯然，當r=1時，圖G的D(r)-點可區別正常邊染色，即G的鄰點可區別正常邊染色；當r≥d(G)時，圖G的D(r)-點可區別正常邊染色，即G的點可區別正常邊染色，其中，d(G)是圖G的直徑.并且，對任意正整數r，有：

引理1設G是階數至少為3的連通圖，則

′a(G)≤′r(G)≤′v(G).

特別地，文獻[4]得到了一些特殊圖類，如圈、扇、輪、完全圖、完全二部圖、樹以及一些聯圖的D(2)-點可區別邊色數，并提出了如下猜想：

猜想2當r≥2時，對任意圖G有

μr(G)≤′r(G)≤μr(G)+1，

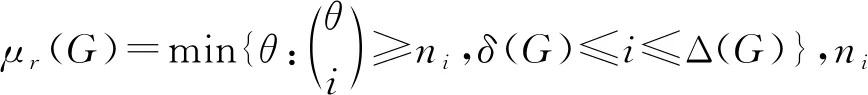
注意，圖的D(r)-點可區別邊染色也稱為r-強邊染色，此概念是Akbari等[5]獨立提出的.

然而，猜想2被Kemnitz等[6]于2014年否定了.他們發現了一類圈Cp，滿足D(2)-點可區別邊色數′2(Cp)=μ2(Cp)+2，其中，

雖然猜想2被否定了，但是確定圖的D(r)-點可區別邊色數上界的問題仍是很有意義的工作.Tian等[8]利用概率方法得到了圖的D(r)-點可區別邊色數一個上界.

猜想3對任意正整數r≥2，存在常數δ0和C，使得對任意不含孤立邊且最小度δ(G)≥δ0的圖G，有

′r(G)≤Δ(G)+C.

劉利群等[10]確定了路與圈的Mycielski圖的D(2)-點可區別邊色數.關于圖的D(r)-點可區別邊染色詳細的研究參見文獻[11].

關于樹的D(r)-點可區別邊染色，Akbari等[5]證明了：對任意樹T, 有′2(T)≤Δ(T)+1，且當T的任意兩個最大度頂點之間的距離大于等于3時，′2(T)=Δ(T)；對最大度Δ(T)≥3的樹T, 有′3(T)≤2Δ(T)-1.

1 預備知識

本文所涉及的圖均為簡單無向圖.設G=(V(G),E(G))是一個圖，其中V(G)和E(G)分別表示G的頂點集和邊集.對頂點v∈V(G)，用d(v)表示v在G中的度數，N(v)表示v的所有鄰點構成的集合.由于G是簡單圖，故d(v)=|N(v)|.若d(v)=1，則稱v為G的葉子.用N1(v)表示v的鄰點中所有葉子構成的集合.圖G的最大度和最小度分別記為Δ(G)和δ(G).對頂點u,v∈V(G)，用d(u,v)表示u和v之間的距離，即u到v最短路的長度.圖G的直徑是指G中兩個頂點之間的最大距離，記為diam(G)，即

diam(G)=max{d(u,v):u,v∈V(G)}.

圖G的一個正常邊染色是指對G的每條邊分配一種顏色,使得任意相鄰的兩條邊的顏色不同.設f是圖G的一個正常邊染色，v∈V(G)，記

C′(v)={f(vw):vw∈E(G)}，

稱C′(v)為頂點v在邊染色f下的色集合.

定義1[4]設f:V(G)→{1,2,…,k}是圖G的一個正常邊染色，如果對G中任意兩個距離不超過r的頂點u,v∈V(G)，有C′(u)≠C′(v)，則稱f為G的D(r)-點可區別邊染色.圖G的D(r)-點可區別邊色數是指對圖G進行D(r)-點可區別邊染色所需要的最小色數，記為′r(G)，即

′r(G)=min{k:G有D(r)-點可區別邊染色}.

圖G的一個正常全染色f是指對G的每個頂點以及每條邊分配一種顏色使得：

(1)對任意uv,vw∈E(G)，u≠w，有f(uv)≠f(vw);

(2)對任意uv∈E(G)，有f(u)≠f(v)，f(u)≠f(uv)，f(v)≠f(uv).

設f是G的一個正常全染色，v∈V(G)，記

C″(v)={f(v)}∪{f(vw):vw∈E(G)}，

稱C″(v)為頂點v在全染色f下的色集合.

定義2[12-13]設f:V(G)∪E(G)→{1,2,…,k}是圖G的一個正常全染色，如果對G中任意兩個距離不超過r的頂點u,v∈V(G)，有C″(u)≠C″(v)，則稱f為G的D(r)-點可區別全染色.圖G的D(r)-點可區別全色數是指對圖G進行D(r)-點可區別全染色所需要的最小色數，記為″r(G)，即″r(G)=min{k:G有D(r)-點可區別全染色}.

類似于鄰點可區別邊染色的概念，當r=1時，圖G的D(r)-點可區別正常全染色即為G的鄰點可區別正常全染色[14]，此問題已被廣泛研究.

文中未給出的定義及符號，請參照圖論文獻[11,15].

2 樹的D(r)-點可區別邊染色

本節討論樹T的D(2)-點可區別邊染色和D(3)-點可區別邊染色，分別得到了對應的邊染色的上界，并給出了線性時間的染色方案.

2.1 樹的D(2)-點可區別邊染色

Akbari等[5]證明了對任意樹T有′2(T)≤Δ(T)+1成立，本小節給出了一種簡單的證明方法.

定理1對任意樹T，可在線性時間給出T的一個使用了不超過Δ(T)+1種顏色的D(2)-點可區別邊染色.

證明設總顏色集C={1,2,…,Δ(T)+1}，T的根節點為u.下面從樹T的根u出發，逐層對T的邊進行染色，并滿足所有關聯的邊已染色的點是D(2)-點可區別的.

由于總顏色數為Δ(T)+1，因此,在染色之后每個頂點x的色集合C′(x)中至少有一種顏色沒有出現.在下面染色中，筆者總是假定c(x)是C′(x)中未出現的一種顏色.

染色方案f如下：

對根節點u，令C′(u)={1,2,…,d(u)}，取c(u1),c(u2),…,c(ud(u))分別為f(uu2)、f(uu3)、…、f(uud(u))和f(uu1)，其中，u1,u2,…,ud(u)是u的子節點.

對其他任意節點x，設x的父節點為y，y的父節點為z(若存在)，且x是y的第m個子節點.令f(xx1)=c(y)，c(x)=f(yym+1)(當y≠u且m=d(y)-1時，c(x)=f(yz))，并令f(xx2),f(xx3), …,f(xxd(x)-1)為在C{c(x),f(xy),f(xx1)}中從大于f(xy)的第一個數開始順序循環所取的d(x)-2種顏色.由于總顏色數為Δ(T)+1，所以|C{c(x),f(xy),f(xx1)}|≥d(x)-2.

易驗證上述染色過程是線性時間的.下面證明此染色方案f是T的D(2)-點可區別邊染色.因為只有度相同的頂點才可能有相同的色集，故下面討論的頂點度均相等，且只討論層數不低于x的節點，低于x的節點同理.

當x是T的葉子時，與x距離不超過2且是葉子的節點一定是y的鄰點，根據上述染色規則可知，它們與x的顏色集不同，即與x是可區別的.下面考慮x不是T的葉子的情況.

(1) 與x距離為2的頂點包括z及y的除x外的子節點.

因為c(x)=f(yym+1)≠f(yy1)=c(z)，所以x與z的色集合不同.對y的除x外的任意子節點yt，因為c(x)≠c(yt)，且f(xy)≠f(yyt)，結合每個節點關聯邊上順序染色的規則可知C′(x)≠C′(yt).

(2) 與x距離為1的頂點只有y.因為f(xx1)=c(y)，即C′(x)包含C′(y)缺少的顏色，故x與y的色集合是不同的.

□

2.2 樹的D(3)-點可區別邊染色

當T是星或雙星時，即T中至多有兩個頂點度數大于等于2，其余頂點的度數都是1時，diam(T)≤3，即T中任意兩個頂點之間的距離都不超過3，因此，′3(T)=|E(T)|.

設T是一棵根為t的樹，v是T中的任一頂點.用d1(v)表示v的鄰點中葉子的數目.

定理2設T是一棵根為t的樹，diam(T) ≥4，且t是T的葉子.令

h=max{d1(x)+d1(y)+2|x,y∈V(G)}，

則T存在使用了不超過max{Δ(T)+2,h}種顏色的D(3)-點可區別邊染色.

證明設k=max{Δ(T)+2,h}，且使用的總顏色集C={1,2,…,k}.下面從樹T的根t出發，逐層對T的邊進行染色，并滿足所有關聯的邊已染色的點是D(3)-點可區別的.

由于k=max{Δ(T)+2,h}≥Δ(T)+2，因此,在染色之后每個頂點x的色集合C′(x)中至少有兩種顏色沒有出現.在下面染色中，筆者總是假定c1(x)和c2(x)是C′(x)中未出現的兩種顏色.

染色方案f如下：

(1)對根頂點t，設其唯一鄰點為u,并令f(tu)=1. 取c1(t)=d(u)，c2(t)=d(u)+1.

(2)設u的孩子節點分別為u1,u2,…,ud(u)-1，令f(uui)=i+1，i=1,2,…,d(u)-1(圖1). 并且，令c1(u)=d(u)+1，c2(u)=d(u)+2.

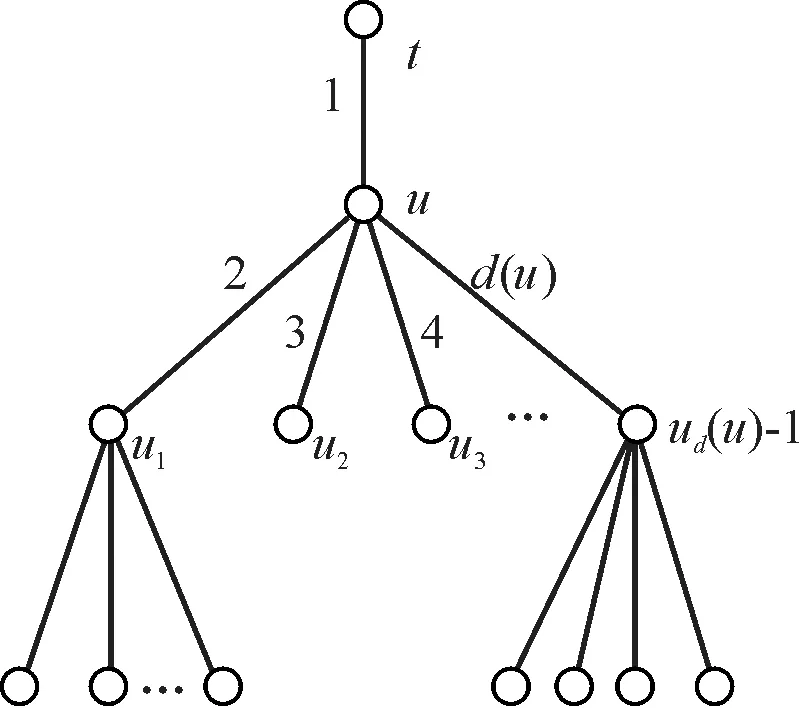
圖1 頂點u的關聯邊的染色方案Fig.1 The coloring of the incident edges of u

(3)從u的孩子節點開始，逐層對u的子孫節點關聯的未染色邊進行染色.

對任意頂點x，設x的父節點為y，y的父節點為z，且x是y的第m個孩子，x的子節點分別為x1,x2,…xd(x)-1. 假設T中頂點y所在層及以上的頂點所關聯的邊均已經染好顏色，如圖2所示.下面對頂點x關聯的未染色邊進行染色.用S(y)表示頂點y的關聯邊中一個端點是葉子的邊的顏色集合，即S(y)={f(yw):w∈N1(y)}.顯然，S(y)中的顏色在x關聯的懸掛邊上是不能出現的.

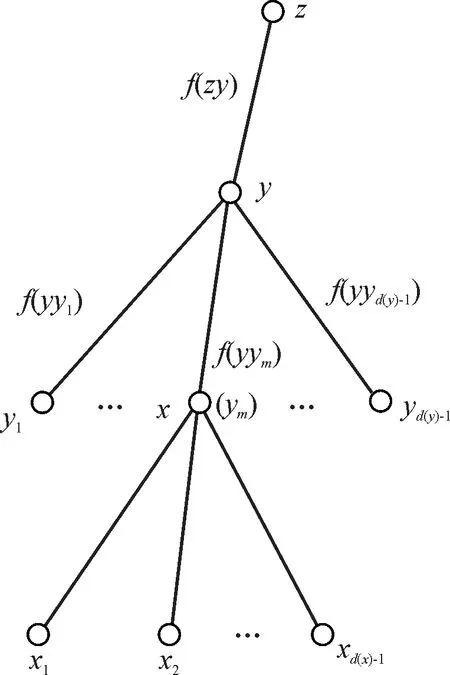
圖2 樹T的結構和染色Fig.2 The structure and coloring of the tree T

若x的子節點都是葉子且d1(y)+d1(x)=k-2，則c1(x),c2(x)待定.若y=u,y的子節點中除x外都是葉子，且d1(y)+d1(x)=k-2, 則c1(x),c2(x)待定.

對其余情況，都令c1(x)=c2(y)，c2(x)=f(yym+1)，當x=yd(y)-1時，令c2(x)=f(zy).

以下對與x關聯的未染色邊進行染色.

R1 若x的子節點中或y的子節點中沒有葉子，則令{f(xx1)}={c1(z),c2(z)}∩{c1(y),c2(y)}，f(xx2),f(xx3),…,f(xxd(x)-1)分別為在C{c1(x),c2(x)}中從大于f(xy)的數開始順序取d(x)-2個顏色，若顏色取盡則回到集合中的第一個顏色.

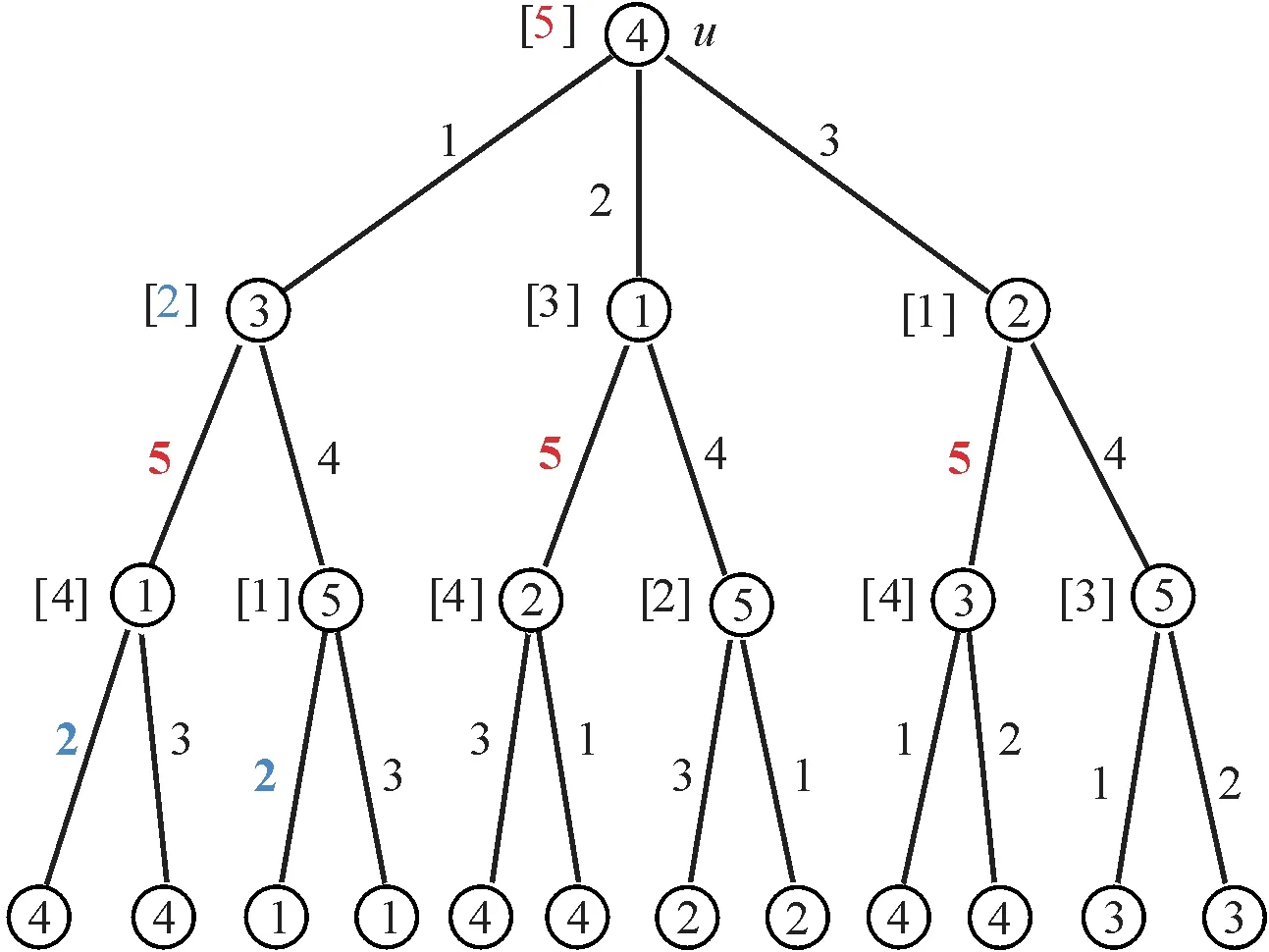
R2 若x和y的子節點中都存在葉子，但x的子節點不都是葉子或d1(y)+d1(x)

R3 若x和y的子節點中都存在葉子，x的子節點都是葉子且d1(y)+d1(x)=k-2，則f(xx1),f(xx2),…,f(xxd(x)-1)分別為在CS(y)中從大于f(xy)的數開始順序取d(x)-1個顏色.

下面證明此染色方案f是T的D(3)-點可區別邊染色.因為只有度相同的頂點才可能擁有相同的色集，故下面討論的頂點度均相等，且只討論層數不低于x的頂點，低于x的頂點同理.設z的父節點為w(若存在).

若x的子節點都是葉子，或者y=u且y的子節點中除x外都是葉子，且d1(y)+d1(x)=k-2，則f(xy)=c1(z)=c2(w)，故x與z和w一定可區別.另外，對z的任意子節點zi，由于c1(y)=c1(zi)=c2(z)，但由染色規則R3可知，C′(x)包含顏色c1(y)，故x與zi是可區別的.

若x是T的葉子，則與x距離不超過3且是葉子的節點一定是y或z的鄰點，根據染色規則R2和R3可知，它們與x的顏色集不同，即與x是可區別的.下面考慮x不是T的葉子的情況.

(1)與x距離為3的頂點包括w及z的除y外的子節點.

由上述染色規則可知，c2(w)=c1(z)=f(yy1), 因此，c2(w)?{c1(x),c2(x)}，此時，若f(xy)≠f(wp)，其中p是w的父節點，則根據每個節點關聯邊上順序染色的規則可知,C′(x)≠C′(w)；若f(xy)=f(wp)，則根據c1(x),c2(x)的選取可知，c2(x)=f(yym+1)，但節點w關聯邊上是順序染色的，因此，也有C′(x)≠C′(w).

設zi是z的除y外的任意子節點.由染色規則R1可知f(xx1)=c1(y)=c2(z)，而c1(zi)=c2(z)，因此，f(xx1)=c1(zi). 這說明f(xx1)∈C′(x)，但f(xx1)?C(zi). 所以，C′(x)≠C′(zi).

(2)與x距離為2的頂點包括z及y的除x外的子節點.由染色規則R1可知f(xx1)=c2(z)，即有f(xx1)∈C′(x)，但f(xx1)?C′(z)， 所以C′(x)≠C′(z).

對y的除x外的任意子節點yt，因為c2(x)≠c2(yt)，且f(xy)≠f(yyt)，結合每個節點關聯邊上順序染色的規則可知C′(x)≠C′(yt).

(3)與x距離為1的頂點只有y.因為c2(x)=c1(y)，c1(x)≠c2(y)，且f(xy)≠f(yz)，所以C′(x)≠C′(y).

綜上可知，f是T的D(3)-點可區別邊染色，即有′3(T)≤max{Δ(T)+2,h}.

□

由定理2的證明過程可知下面結論成立.

推論1對任意樹T，diam(T)≥4，可在線性時間給出T的使用不超過max{Δ(T)+2,h}種顏色的D(3)-點可區別邊染色.

推論2設T是一棵樹，diam(T)≥4，且h=max{d1(x)+d1(y)+2|x,y∈V(G)}≤Δ(T)+2, 則′3(T)≤Δ(T)+2.

3 樹的D(r)-點可區別全染色

本節在樹的D(2)-和D(3)-點可區別邊染色基礎上，進一步討論樹的D(2)-和D(3)-點可區別全染色.

定理3對任意樹T，可在線性時間給出T的一個使用了不超過Δ(T)+3種顏色的D(2)-點可區別全染色.

證明對T中的邊采用定理3中的染色方案對其進行染色，可得到T的一個使用了不超過Δ(T)+1種顏色的D(2)-點可區別邊染色.然后對T的頂點用兩種新顏色進行正常點染色，則所得到的染色f是T的D(2)-點可區別全染色.

□

事實上，通過定理3的證明過程得到的染色f也是T的D(3)-點可區別全染色.因為T中任意兩個距離為3的頂點的點顏色是不同的，故它們的色集合也是不同的.所以，定理4成立.

定理4對任意樹T，可在線性時間給出T的一個使用了不超過Δ(T)+3種顏色的D(3)-點可區別全染色.

□

另外，可通過定理2來證明定理4，具體證明過程如下：

對任意給定的樹T，不妨設其頂點數大于等于3，給T的每個頂點上增加一條新的懸掛邊，所得到的圖仍是一棵樹，記為T*. 即有：

V(T*)=V(T)∪{v*:?v∈V(T)},

E(T*)=E(T)∪{vv*:?v∈V(T)}.

顯然，有Δ(T*)=Δ(T)+1，且

max{d1(x)+d1(y)+2|x,y∈V(T*)}=

2<Δ(T*)+2,

利用定理2的證明過程和推論2可知，在線性時間可得到T*的一個使用了不超過Δ(T*)+2種顏色的D(3)-點可區別邊染色f*.下面在f*的基礎上定義T的全染色f如下：

(1)對任意頂點v∈V(T)，令f(v)=f*(vv*)；

(2)對任意邊uv∈E(T)，令f(uv)=f*(uv)；

由于f*是T*的D(3)-點可區別邊染色，因此,對T中任意兩個相鄰的頂點u和v，邊uu*和vv*在f*下的顏色是不同的，由f的定義可知，f(u)≠f(v),所以，f是T的一個正常全染色.另外，根據f與f*的關系可知，對T中任意頂點x，有C″(x)=C′(x)，所以f是T的D(3)-點可區別全染色.

□

下面，對定理3的結論進行改進，可得到樹T的一個使用了不超過Δ(T)+2種顏色的D(2)-點可區別全染色.

定理5設T是一棵樹，則

″2(T)≤Δ(T)+2.

證明當Δ(T)≤2時，易驗證″2(T)≤4.

下面考慮Δ(T)≥3的情況.設使用的總顏色集C={1,2,…,Δ(T)+2}，樹T的根節點是u，且d(u)=Δ(T). 下面從樹T的根u出發，逐層對T的點和邊進行染色，并滿足所有關聯的邊和點本身已染色的頂點是D(2)-點可區別的.

由于總顏色數為Δ(T)+2，因此,在染色之后每個頂點x的色集合Cii(x)中至少有一種顏色沒有出現.在以下染色中，筆者總是假定c(x)是Cii(x)中未出現的顏色.

染色方案f如下：

對根節點u，令C″(u)={1,2,…,d(u)}，f(u)=d(u)+1,取c(u1),c(u2),…,c(ud(u))分別為f(uu2),f(uu3),…,f(uud(u)),f(uu1)，其中,u1,u2, …,ud(u)是u的子節點.

對其他任意節點x，設x的父節點為y，y的父節點為z，x的子節點分別為x1,x2,…xd(x)-1，并且x是y的第m個子節點.

如果x是T的葉子，則只對頂點x進行染色即可.此時，令f(x)=c(y).

如果x不是T的葉子，則：

(1)令f(xx1)=c(y)，c(x)=f(yym+1)(當x≠ud(u)且m=d(y)-1時，令c(x)=f(yz))；

(2)取f(x)∈C{f(y),f(xy),f(xx1),c(x)}；

(3)令f(xx2),f(xx3),…,f(xxd(x)-1)為在C{c(x),f(x),f(xy),f(xx1)}中從大于f(xy)的第一個數開始順序循環所取的d(x)-2種顏色，如圖3所示(圖中[p]表示該頂點缺少的顏色為p).

圖3 一棵最大度為3的樹的D(2)-點可區別全染色

由于|C{c(x),f(x),f(xy),f(xx1)}|≥Δ(T)+2 -4≥d(x)-2，故上述染色方案(3)是有效的.

下面證明此染色方案f是T的D(2)-點可區別全染色.只證明任意頂點x與其祖先頂點是可區別的.

當x是T的葉子時，與x距離不超過2且是葉子的節點一定是y的鄰點，根據上述染色規則可知，y的所有關聯邊的顏色是不同的，但y的所有葉子鄰點的顏色都是c(y)，因此,x與y的其他葉子鄰點的色集合是不同的.下面考慮x不是T的葉子的情況.

(1)與x距離為2的頂點包括z及y的除x外的子節點.

因為f(xy)=c(z)，即C″(x)包含C″(z)缺少的顏色，所以x與z的色集合是不同的.對y的除x外的任意子節點yt，因為c(x)≠c(yt)，且f(xy)≠f(yyt)，所以，結合每個節點關聯邊上順序染色的規則可知，C″(x)≠C″(yt).

(2)與x距離為1的頂點只有y.因為f(xx1)=c(y)，即C″(x)包含C″(y)缺少的顏色，故x與y的色集合是不同的.

綜上所述，f是T的D(2)-點可區別全染色，因此，″2(T)≤Δ(T)+2.

□

4 結 論

本文對樹的D(2)-點可區別邊(全)染色和D(3)-點可區別邊(全)染色進行了討論，分別得到染色數的上界，并給出了線性時間的染色方案.

樹的D(r)-點可區別邊色數主要受到距離不超過r的葉子頂點數目的影響.特別地，當r比較大時，影響更為明顯.

對任意k≥4，Akbari等[5]構造了樹T，滿足

′k-vd(T)≥Δ(T)(Δ(T)-1)|k/2|-1，

其構造如下：令u是T的根，讓T中與u的距離小于|k/2|的頂點的度數均為Δ(T)，與u的距離等于|k/2|的頂點的度數均為1. 可以看出，T中包含Δ(T)(Δ(T)-1)|k/2|-1個度為1的頂點，且任意兩個的距離不超過k，因此，′k-vd(T)≥Δ(T)(Δ(T)-1)|k/2|-1.

但樹的D(r)-點可區別全色數受到距離不超過r的葉子頂點數目的影響較小，因為在全染色下每個頂點都有顏色，從而增加了備選的色集合.

對圖G, 令

其中，ni表示度為i且任意兩點間的距離不超過β的頂點的最大數目.

易驗證，ηr(G)是圖G具有D(r)-點可區別全染色所需顏色數的一個下界，即″r(G)≥ηr(G).

張忠輔等[12-13]猜想對任意圖G有

ηr(G)≤′r(G)≤ηr(G)+1，