基于CPFS結構理論的“實數”復習課教學設計

陸文婷 韋 宏

（南寧師范大學數學與統計學院 廣西·南寧 530299）

喻平教授根據數學學習心理的特征，提出了“CPFS”結構理論。該理論包含“概念域”“概念系”“命題域”“命題系”。教學實踐中，往往會出現這樣的現象：在概念學習中，當學生學習了一個概念之后，在具體應用這個概念時會出現類型各異的錯誤，或者是沒有把握概念的內涵，無法辨認概念的反例，或者是不能理解概念的變式。在命題學習中，當學生學習了一個命題，特別是學習了一組命題之后，往往不會靈活應用這些命題。產生這些現象的原因是多方面的，喻平教授認為，個體的CPFS結構的優良與否是一個主要因素。[1]因此，在數學教學中需要教師在教學過程中構建和完善學生的CPFS 結構。

實數在中學的數學學習中占有著十分重要的地位，實數不僅是初中階段學習的二次根式、一元二次方程以及解三角形等知識的基礎，由于實數密切聯系了高中許多知識，所以它也是學習高中數學內容的基礎。從歷年的中考題中可以知道，對于實數的考查都結合其他知識點。從概念角度來看，它可以聯系研究數的相反數、絕對值、數軸等。從運算角度來看，在實數范圍內可以對正數和0 進行開平方運算。從特殊實數的形式二次根式來看，可以為解決“二次問題”，即一元二次方程、二次函數等提供基礎。因此，學生在初中階段的學習中應建立起“實數”的知識體系，為以后學習虛數提供數學思想和方法去分析、解決相關問題。本文從實數這個具體實例出發，建立關于實數的概念體系，進而完善學生的CPFS結構。

1 教學目標與重、難點

本節內容是人教版七年級下冊第六章知識。喻平教授指出，對一個概念的理解首先應當從不同側面去考察它，形成關于這個概念的概念域；其次，要梳理與該概念有抽象關系的概念體系，形成這個概念的概念系。[1]因此，確定了本節課的教學目標與重、難點如下所示。

教學目標：學生能夠掌握實數有關概念；學生能夠建構實數的知識網絡結構；學生能夠體驗到在建構知識網絡過程中的數的擴充發展和數學思想方法應用的過程中數學是發展的。

教學重點和難點：學生自主建構實數的知識網絡結構的過程。

2 CPFS 結構理論指導構建實數的知識網絡結構

喻平教授在其CPFS 結構理論中，強抽象是指通過引入新的特征來強化原結構A，使獲得的新的概念或理論B，B 是原型A 的特例，則稱A 到B 的抽象為強抽象，或稱A 與B 之間的關系存在強抽象關系。弱抽象是指從一個數學結構A 中選取某一特征或側面加以抽象，從而獲得比原結構A 更廣的結構B，使原結構A 成為結構B 的特例，就稱A 到B 的抽象為弱抽象，或稱A 與B 之間存在弱抽象關系。[1]

這里的強抽象關系也就是一種上位學習，即一般到特殊。而弱抽象則是下位學習，即特殊到一般。實數是有理數和無理數的上位概念，也就是說，從有理數、無理數到實數是一種弱抽象關系；從平方根到二次根是一種強抽象關系。在這個概念結構中，蘊涵了數形結合思想（數軸與實數的對應）、類比思想（類比有理數的分類對實數進行分類）和一般化思想（表現為強抽象關系或弱抽象關系）（圖1）。[3]

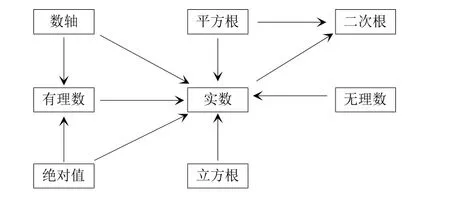
圖1

3 實數概念體系教學過程設計

3.1 創設問題情境，以問題為驅動

問題1 我們在七年級的時候已經學習了實數這個概念，那么同學們能不能聯系實數的有關知識去建立一個關于知識結構圖？

設計意圖：直接設置以實數為主的知識結構圖的問題，可以讓學生明確本節課的學習目標，學生進入頭腦風暴快速調動儲存的相關知識。

3.2 設置問題鏈完善知識網絡結構

問題2 回顧一下目前為止，我們最開始學習的數是什么數？

學生：小學學習的正整數。

問題3 由于實際生活的需求，我們又學習到什么數？

學生：分數、負數、小數等。

問題4 這些數之間有什么聯系？有什么區別？

學生：這些數按照不同的分類可分為有理數和無理數。

問題5 一起回顧有理數和無理數的定義，它們有什么區別與聯系？它們共同組成什么？

問題6 按照學習過的有理數分類方式，你能不能對實數進行分類？所有數概念之間又有什么聯系？這其中體現了什么數學思想方法？

設計意圖：通過對數的梳理，讓學生再次體驗知識產生的緣由，明晰新舊知識之間出現的關聯關系，以及體悟知識發展的動因，習得探究數學知識邏輯性的方法。并類比有理數的分類方法對實數進行分類，以此讓學生明確數學思想方法的重要。最后，學生體驗到數的概念是怎樣從正整數逐步發展到實數的。

問題7 我們在研究有理數的時候，一般都研究些什么？

學生：相反數、絕對值、數軸等。

問題8 相反數、絕對值和數軸是怎樣定義的？

問題9 對于實數，我們又是怎樣研究它的相反數、絕對值和數軸的呢？它們與研究有理數這些性質時有什么聯系與區別？這其中體現了什么數學數學方法？

設計意圖：實數是有理數的上位知識，從研究有理數的相關性質來研究實數的相關性質，也就是從有理數到實數是弱抽象關系，即特殊到一般的關系。從實數到有理數是強抽象關系，即一般到特殊的關系。在與學生探討的過程中，需要指出這些關系，有利于學生體會知識之間的聯系。通過類比思想從有理數中來學習實數的相關性質，并且結合數軸研究，其中體現了數學解題的類比思想和數形結合思想。

問題10 從運算角度來看，隨著數的擴充，數的運算有什么發展？加法與乘法的運算律在實數中始終保持不變嗎？

問題11 回顧平方根和立方根的概念，乘方運算與立方運算有什么關系？

問題12 作為一類特殊實數一般形式的二次根式，它與算術平方根有什么關系？它的運算與實數的運算之間又有什么關系？與整式的運算之間又有什么關系？

設計意圖：從運算這一脈絡出發梳理知識之間的聯系，不僅可以幫助學生快速建構實數知識網絡結構，而且可以讓學生體會在數系發展中運算是基本一致的。這樣為以后解決復數的運算提供了思想方法。

教師在與學生解決這些問題的同時，需要在黑板上畫出實數的知識網絡結構。

3.3 鞏固練習，加深概念體系的認識

通過問題鏈的解決，從多角度、多重層次去揭示實數的概念內涵，并且明示各知識概念間的關系和揭示蘊涵在概念網絡結構中的數學思想方法。為了加強對概念網絡結構的理解，需要結合一些練習鞏固。喻平教授的CPFS 結構理論指出，加強概念需要在兩個水平上應用，即知覺水平上應用與思維水平應用。

第一，在知覺水平上的應用。

例1 判斷下列說法是否正確：

（1）無限小數都是無理數；（2）無理數都是無限小數；（3）帶根號的數都是無理數；（4）所有有理數都可以用數軸上的點表示，反過來，數軸上的所有點都表示有理數；（5）所有實數都可以用數軸上的點表示，反過來，數軸上的所有點都表示實數。

例2 有沒有最小的正整數？有沒有最小的正實數？有沒有最小的實數？有沒有最小的無理數？

以上兩題是這個體系的簡單應用，考查了實數相關的有理數、無理數等概念結構。

第二，在思維水平上的應用。

例 3 已知（x-1）2=4,求 x 的值。

例4 已知|x|<2 ，x 是整數，求x 的值，并在數軸上表示求得的數。

例5（2019 湖北黃石）

以上是實數結合方程、三角函數以及二次函數等的題目，解決題目需要學生通過題目信息從已有知識結構中提取和選擇相關的概念和命題來解決當前的題目。

4 結束語

復習課的作用就是通過整理零散的知識成為一個知識之間含有相關關系的知識網絡結構，使知識條理化、系統化。根據CPFS 結構理論，當學生擁有良好的知識結構時，學生能夠更好地提取知識解決問題。因此，教師在授課中提高學生建構知識網絡結構的能力，有利于學生的數學學習。