錘片式粉碎機主軸機構(gòu)的多目標優(yōu)化
徐偉,曹春平
(南京理工大學 機械工程學院,江蘇 南京 210094)
0 引言
錘片式粉碎機是重要的農(nóng)產(chǎn)品加工裝備,它有著構(gòu)造簡單、使用方便、粉碎效率較高等優(yōu)點,因此在糧食及飼料等農(nóng)業(yè)方面應用廣泛[1]。主軸是錘片式粉碎機系統(tǒng)的關鍵機構(gòu)之一。主軸上安裝有轉(zhuǎn)子,通過兩個帶座軸承固定,其作用是傳遞電動機所給的轉(zhuǎn)矩,其性能的優(yōu)劣將直接關系到粉碎機加工產(chǎn)品質(zhì)量的好壞。錘片式粉碎機在工作時,利用電動機帶動轉(zhuǎn)子錘片高速轉(zhuǎn)動來撞擊物料,從而達到粉碎飼料的目的[2]。目前國內(nèi)外對錘片式粉碎機的研究基本集中在粉碎室寬度、錘片末端到篩片的距離、轉(zhuǎn)子直徑以及吸風裝置的設置等因素對錘片式粉碎機粉碎效率的影響,而對于粉碎機在結(jié)構(gòu)方面的研究一直都很少[3]。鑒于此,以江蘇某集團一經(jīng)典型號的錘片式粉碎機為研究對象,通過分析轉(zhuǎn)子的工作特性,利用ANSYS Workbench軟件對主軸進行多目標分析,以轉(zhuǎn)子上的主軸最大應力與最大應變?yōu)槟繕撕瘮?shù),對比3種不同的優(yōu)化方案,確定一種最優(yōu)方法來達到最佳的設計效果。
1 主軸的工作特性分析
本次研究粉碎機的電動機和主軸使用的是彈性套柱銷聯(lián)軸器直聯(lián)傳動,這種傳動裝置兩個顯著優(yōu)點是傳動軸沒有側(cè)向壓力,傳遞功率可以很大。另一方面,由于本次研究的設備粉碎的對象主要是大米、小麥、大麥等小型顆粒物,在粉碎機工作時,錘片擊打飼料時錘片的速度變化并不明顯,因此對稱的兩排錘片因為速度差產(chǎn)生的離心力差很小,可以忽略不計。綜上所述,轉(zhuǎn)子上的主軸主要受如下幾個力:安裝在主軸上相對的兩排錘片會存在質(zhì)量差,所以兩排錘片在繞著主軸轉(zhuǎn)動時對主軸產(chǎn)生的離心力會有較大的差值,稱為離心力差FN;安裝在主軸上整個轉(zhuǎn)子的重力G;電動機傳遞給主軸的轉(zhuǎn)矩T。
下面具體分析這幾個力:
1) 計算離心力差:按照某集團的錘片質(zhì)量安裝要求,徑向相對稱的兩組錘片總質(zhì)量相差不得超過2g,按照最大的質(zhì)量差利用公式(1)進行計算:
(1)
式中:v表示錘片質(zhì)心的速度;r表示質(zhì)心到主軸軸心的距離。其中v=72m/s,r=232mm,所以F=44.69N。可以看出離心力差與轉(zhuǎn)子自重和轉(zhuǎn)矩相比很小,在進行受力分析可以忽略不計。
2) 計算重力:利用SolidWorks軟件對錘片式粉碎機中的轉(zhuǎn)子進行建模,定義材料屬性之后,經(jīng)過計算得出整個轉(zhuǎn)子的重力為1 950N。全部加載到主軸的質(zhì)心處即中心處。
3) 計算轉(zhuǎn)矩:粉碎機的主要參數(shù)如表1所示,主軸受到的轉(zhuǎn)矩利用公式(2)計算:
(2)

表1 粉碎機的主要參數(shù)
主軸的受力圖如圖1所示。
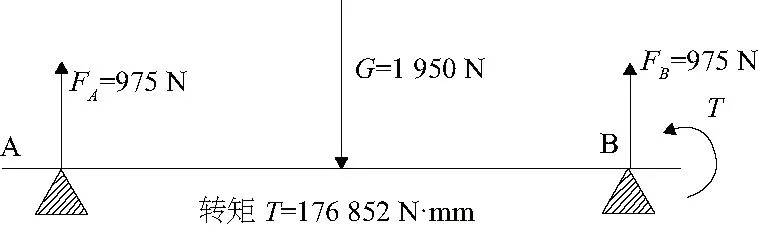
圖1 主軸受力示意圖
2 主軸的數(shù)值模擬與試驗驗證
錘片式粉碎機相比較于其他粉碎機,具有結(jié)構(gòu)簡單、生產(chǎn)效果較高、適應性較強等優(yōu)點。對粉碎機粉碎效率的研究大多數(shù)采用試驗的方式,這種方式成本高,比較耗時,而對于本次的研究目標來說可以通過數(shù)值模擬方式提高研究效率。首先建立簡化的物理模型,進而根據(jù)物理模型建立有限元模型,進行有限元分析,最后進行主軸的應變測試試驗來驗證數(shù)值計算模型的可行性。
2.1 結(jié)構(gòu)模型
利用Solidworks軟件對主軸進行建模,為了使計算結(jié)果更加精準,有必要對主軸模型進行一些簡化。合理的簡化模型可以節(jié)約計算資源、縮短計算運行時間,提高分析效率,所以可以對主軸的圓孔、鍵槽等一些不需要的特征進行簡化并刪除[4]。圖2是主軸的簡化物理模型。

圖2 主軸的結(jié)構(gòu)模型
2.2 靜力學分析
將建好的主軸物理模型導入到ANSYS Workbench軟件中之后,對主軸進行網(wǎng)格劃分。在進行計算之前,在軟件中添加分析所要得到結(jié)果的模塊,也就是主軸的應力和主軸的應變分析。根據(jù)上述的計算結(jié)果在主軸上插入載荷,由于主軸是與聯(lián)軸器直接相連,因此將主軸與兩端軸承座配合的兩個面添加圓柱面約束,加載載荷時選擇軸承載荷類型。計算結(jié)果如圖3-圖4所示。

圖3 主軸的應力分析

圖4 主軸的應變分析
為了對上述數(shù)值計算模型進行驗證,對錘片式粉碎機進行主軸測量試驗。由于上述數(shù)值模擬主軸的應力和應變是在同一加載條件和同一約束得到的模擬結(jié)果,所以對數(shù)值計算進行驗證時只需要驗證一方面即可。在這里驗證最大應變要簡單得多。因此選擇對主軸進行應變測量試驗。考慮到轉(zhuǎn)子上主軸的受力特點以及多通道同步測量的要求,并滿足橋路溫度自補償?shù)囊螅瑧儨y量采用全橋電路。采用特制的應變片,將錘片式粉碎機的操作門打開,沿圓周方向90°間隔粘貼在主軸上進行試驗[5]。連接線路圖和現(xiàn)場測試圖如圖5、圖6所示。
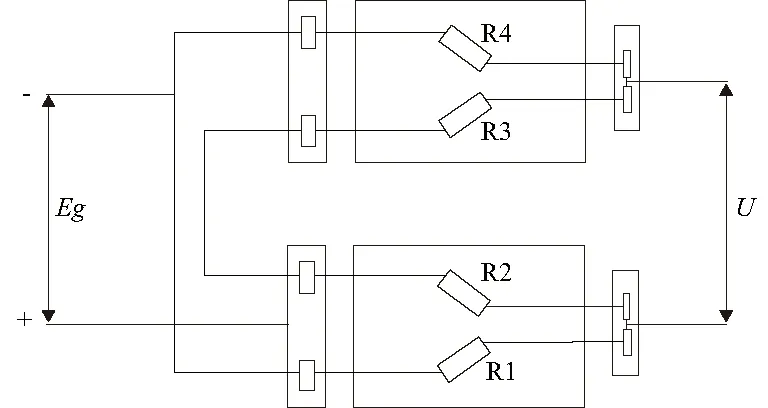
圖5 全橋電路線路圖

圖6 現(xiàn)場測試圖
2.3 驗證結(jié)果
按照上述步驟完成測試,用應變儀來讀出應變片的阻值變化,最后根據(jù)公式(3)計算:
(3)
其中:ε為應變值,K為靈敏度系數(shù)。測得主軸上應變最大值為ε=6.8×10-5,與數(shù)值模擬相差13.9%。因為在進行試驗時是按照仿真數(shù)據(jù)來進行測試,在確定主軸最大應變位置處會有誤差,因此測得數(shù)據(jù)會有一定的誤差,但也在可允許的范圍,數(shù)值模型可用于主軸的結(jié)構(gòu)優(yōu)化。
3 主軸優(yōu)化模型的建立
3.1 優(yōu)化計算的數(shù)學模型
本研究提出了3種優(yōu)化方案,2種單目標函數(shù)優(yōu)化方案和1種統(tǒng)一目標函數(shù)優(yōu)化方案。
1) 方案1:以減小應力為目的,應盡可能減小主軸的最大應力σmax,目標函數(shù)就是:
minF1(X)=σmax
(4)
2) 方案2:與方案1相反,以減小應變?yōu)槟康模瑧M可能減小主軸的最大應變εmax,目標函數(shù)就是:
minF2(X)=εmax
(5)
3)方案3:根據(jù)平方和加權法思想,分別求出單個目標函數(shù)的最優(yōu)值fi。由于各單個目標函數(shù)通常無法同時最優(yōu)化,但在這里應盡量趨近理想點,所以,可構(gòu)造出加權評價函數(shù),將多目標問題轉(zhuǎn)化為統(tǒng)一目標函數(shù)進行優(yōu)化[6],即:
(6)
通過公式(6)求出該式的最優(yōu)解,便可得到原多目標函數(shù)的最佳值。W為加權因子,可以反映出各個目標在優(yōu)化問題中的重要程度。由于應力應變對于主軸來說同等重要,因此可以取W=1。據(jù)此可構(gòu)建本研究多目標優(yōu)化問題的統(tǒng)一目標函數(shù):
(7)
式中σmaxΔ以及εmaxΔ分別為最大應力與最大應變的最優(yōu)值。
3.2 優(yōu)化變量的確定
通過上述分析,開始對主軸的各個結(jié)構(gòu)參數(shù)進行優(yōu)化設計,但在優(yōu)化過程中,因變量繁多,通常不會全部選擇作為優(yōu)化變量,只選擇對目標函數(shù)比較敏感的設計變量進行優(yōu)化[7]。主軸的各結(jié)構(gòu)參數(shù)如圖7所示:總共有L1-L6以及D1-D612個優(yōu)化變量,其中D1=D5,D2=D4,L1=L5,L2=L4。
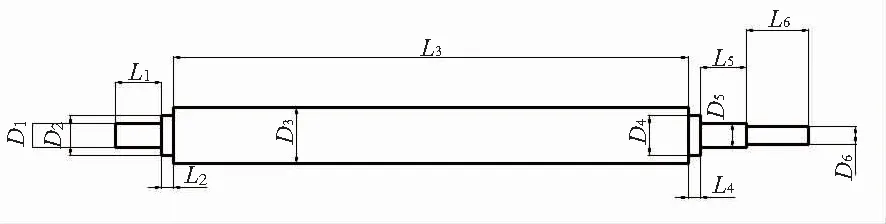
圖7 主軸的優(yōu)化變量
3.3 主軸結(jié)構(gòu)靈敏度分析
利用ANSYS軟件中的設計研究模塊對各設計變量進行分析,計算上述優(yōu)化變量對目標函數(shù)最大應力與最大應變的影響程度,如表2所示。
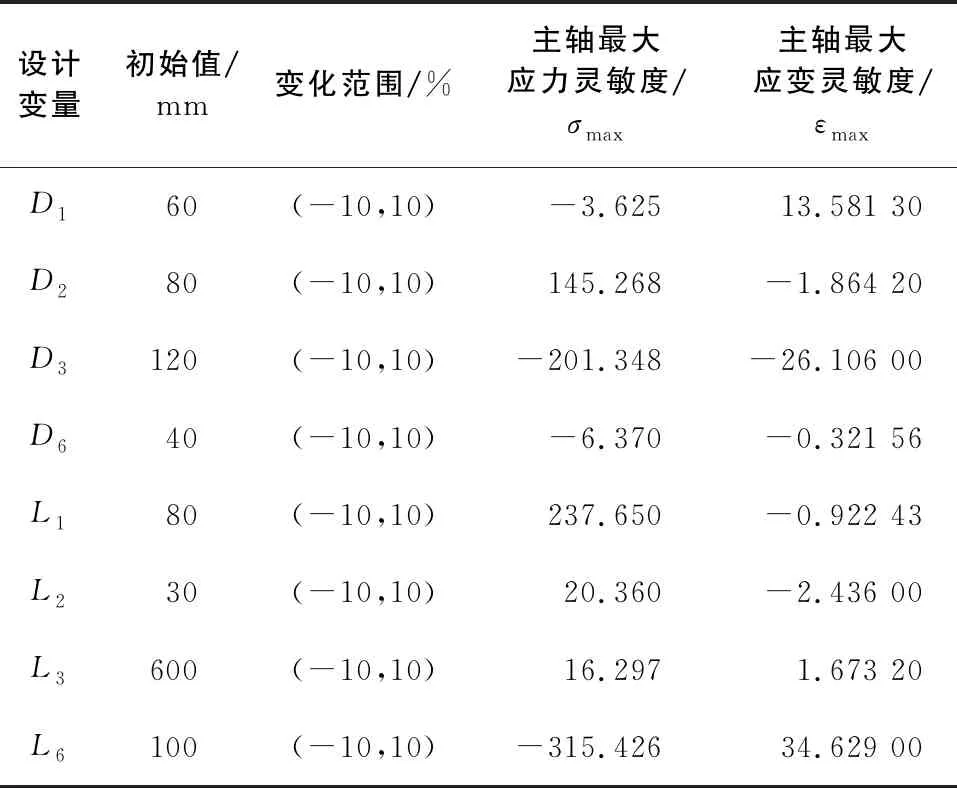
表2 靈敏度分析結(jié)果
分析表2可知,對主軸的最大應力靈敏度排序為
L6>L1>D3>D2>L2>L3>D6>D1,
其中L6、L1、D3、D2變量對主軸的最大應力的影響較大,并且D3、L6呈負相關性;對主軸的最大應變靈敏度排序為
L6>D3>D1>L2>D2>L3>L6>D6,
其中L6、D3、D1變量對主軸的最大應變的影響較大,并且D3呈負相關性。
綜上所述,當采用方案1的時候,也就是使得主軸的最大應力最小,優(yōu)化變量為:
X1=[L6,L1,D3,D1]T
當采用方案2的時候,也就是使得主軸的最大應變最小,優(yōu)化變量為:
X2=[L6,D3,D1]T
當采用方案3的時候,需要綜合考慮優(yōu)化變量對主軸的最大應力與最大應變的影響程度,所以優(yōu)化變量為[8]:
X3=X1∪X2=[L6,L1,D3,D2,D1]T。
4 主軸結(jié)構(gòu)的優(yōu)化結(jié)果
確定了3種方案的優(yōu)化變量以后,利用ANSYS Workbench軟件對上文3種方案進行優(yōu)化,主軸優(yōu)化方案經(jīng)過16次迭代后收斂,最優(yōu)結(jié)果序列為17。3種方案的收斂情況如圖8-圖11所示。
方案1
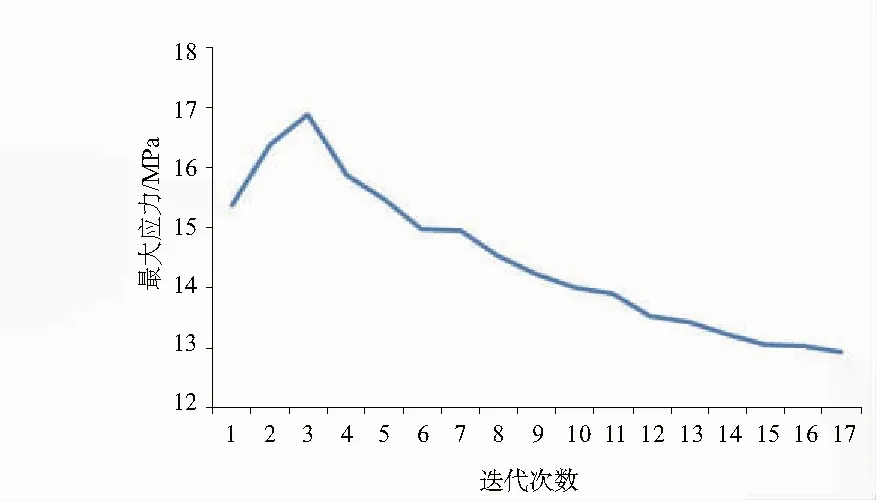
圖8 主軸的應力優(yōu)化收斂曲線
方案2
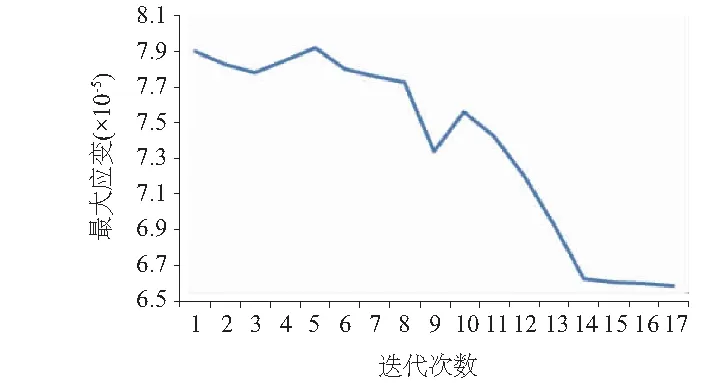
圖9 主軸的應變優(yōu)化收斂曲線
方案3
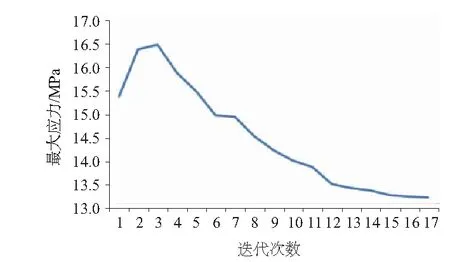
圖10 主軸的應力優(yōu)化收斂曲線
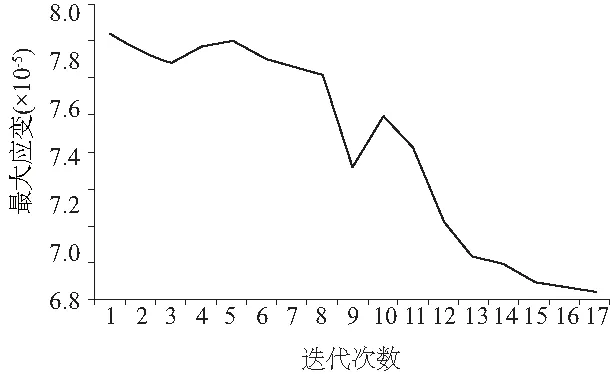
圖11 主軸的應變優(yōu)化收斂曲線
將3種方案優(yōu)化之后整理的數(shù)據(jù)與初始數(shù)據(jù)進行對比分析,結(jié)果如表3所示。
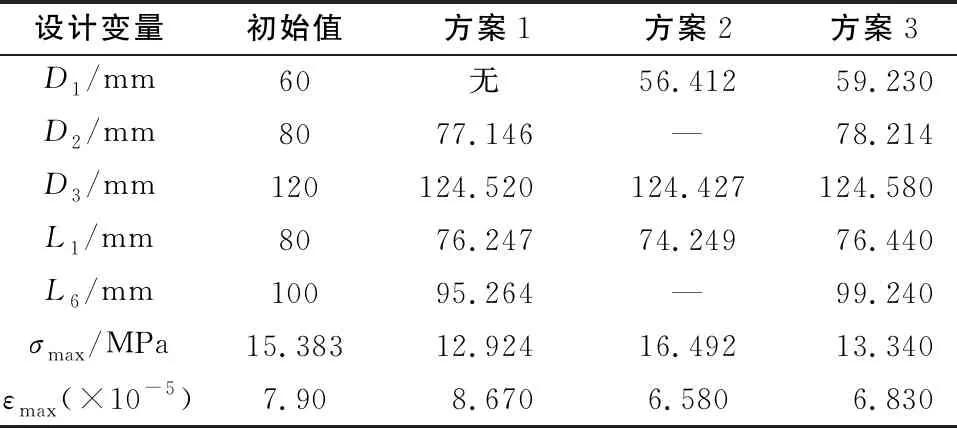
表3 優(yōu)化結(jié)果對照表
由表3可知,最大應力的初始值為15.383MPa,最大應變?yōu)?.90×10-5。對于方案1來說,經(jīng)過優(yōu)化以后最大應力為12.924MPa,下降了15.98%,但最大應變εmax卻上升了9.7%;在方案2中,經(jīng)過優(yōu)化以后最大應變下降了16.7%,但是最大應力卻上升了7.21%;在方案3中,經(jīng)過優(yōu)化之后最大應力下降了13.2%,并且最大應變同時也下降了13.5%。綜上所述,對于方案1來說,雖然在降低最大應力這個單個目標上優(yōu)化效果比較突出,但是同時也導致最大應變上升;在方案2中,也是存在這樣的問題,因此這種只得到單個目標優(yōu)化效果的,在通常情況下是不采納的。對于方案3來說,對于主軸的最大應力和最大應變兩個目標優(yōu)化效果雖不及上述兩種方案中單個目標的優(yōu)化效果,但是都得到了不錯的優(yōu)化效果,對于這種多目標優(yōu)化問題來說,這種方案無疑是最佳選擇,因此,對于主軸的最大應力與最大應變優(yōu)化方案選擇優(yōu)化方案3。
5 結(jié)語
1) 對某集團的錘片式粉碎機進行了研究,通過分析粉碎機主要結(jié)構(gòu)轉(zhuǎn)子的工作特性,并對主軸進行受力分析,得出了主軸在粉碎機工作時的受力模型,為運用軟件對主軸進行靜力學分析奠定基礎。數(shù)值模擬結(jié)束之后提出用測試主軸最大應變的方法來驗證其合理性。針對減小主軸的最大應力與最大應變問題提出3種優(yōu)化方案,其中包括2種單目標優(yōu)化方案和1種統(tǒng)一目標的優(yōu)化方案,為數(shù)值模擬優(yōu)化提供理論支撐。
2) 確定主軸的設計變量,運用ANSYS Workbench對設計變量進行仿真優(yōu)化。
3) 在3種方案中,第3種即用平方和加權法思想建立的統(tǒng)一目標函數(shù)優(yōu)化方案綜合優(yōu)化效果最佳,因此選擇第3種方案為這次優(yōu)化仿真的最終方案。優(yōu)化后主軸的最大應力下降了13.2%,最大應變同時也下降了13.5%。

