存在議價能力和副產(chǎn)品協(xié)同生產(chǎn)的制造商最優(yōu)產(chǎn)量決策

周 品, 徐 和, 陸 芬

(1.華中科技大學管理學院，湖北 武漢 430074；2.武漢科技大學管理學院，湖北 武漢 430081)

1 引言

隨著環(huán)境污染和生態(tài)問題日益加劇，公眾環(huán)境保護的意識逐漸增強，對生活質量提出了更高的要求。同時各國政府相繼出臺了相關的環(huán)境保護措施來進一步規(guī)范和管制企業(yè)的污染行為。基于公眾、政府的雙重壓力以及企業(yè)自身社會責任感的考慮，制造企業(yè)需采取有效措施對廢棄污染物進行處理以減少對環(huán)境的污染。在現(xiàn)實中，常見的廢料處理方式有兩種：一是企業(yè)自身通過傳統(tǒng)方式進行處理，比如美鋁秦皇島工廠產(chǎn)生的具有高資源利用價值的危險廢物含油硅藻土主要通過水泥窯將其進行焚燒處理[1]；二是將廢料外包給處理廠處理，比如蔗糖廠在生產(chǎn)中產(chǎn)生的甘蔗渣主要是賣給下游的造紙廠。可以看到這兩種方式存在顯著的差異，在第一種處理方式中，企業(yè)需要花費一定的處理成本，同時該方式對廢料處理之后并未將廢料轉化為新產(chǎn)品進行銷售；在第二種處理方式中，企業(yè)可以從廢料的交易中獲得收益，同時處理廠通過專門的技術對廢料進行加工，最終生產(chǎn)出新產(chǎn)品(如：紙)來銷售。此外，在實踐中，廢料的交易價格并非由單個企業(yè)(如上游制造企業(yè))來設定的，往往是上游的制造商和下游的處理廠通過協(xié)商議價的方式確定最終的廢料交易價格，如廣西制糖廠將蔗渣打包外賣給制漿造紙企業(yè)的出廠價為250元/噸[2]，該交易價格主要是雙方協(xié)商確定的。鑒于此，本文分析在供應鏈成員(制造商和處理廠)存在議價能力時，制造商如何確定主產(chǎn)品的產(chǎn)量？成員之間如何通過議價決定廢料的交易價格？議價能力會對成員的均衡利潤產(chǎn)生怎樣的影響？對于制造商而言，采取副產(chǎn)品協(xié)同生產(chǎn)是否總是有利的？

本研究主要與副產(chǎn)品協(xié)同生產(chǎn)下的最優(yōu)決策和供應鏈環(huán)境下的納什議價模型兩個領域的研究密切相關。在副產(chǎn)品協(xié)同生產(chǎn)的研究方面，目前的研究文獻相對較少。其中Lee[3]研究了壟斷制造商在可以將廢料轉化為可銷售的副產(chǎn)品時的最優(yōu)產(chǎn)量和價格決策。Lee和Tongarlak[4]在零售業(yè)的背景下分析了需求不確定情形下企業(yè)如何決定最優(yōu)的價格和副產(chǎn)品協(xié)同生產(chǎn)策略。程晉石等[5]研究了由制造商和再制造商組成的再制造供應鏈系統(tǒng)，考慮雙方是否實施副產(chǎn)品生產(chǎn)的四種市場結構，得出各種情形下的最優(yōu)決策。上述研究僅考慮廢料是通過自身處理的情形，而在現(xiàn)實中，由于廢料處理的技術限制，企業(yè)往往通過第三方處理廠來處理。本研究考慮在供應鏈成員之間存在議價能力的情形下，上游企業(yè)如何進行主產(chǎn)品的最優(yōu)產(chǎn)量決策以及如何通過協(xié)商議價方式確定最優(yōu)的廢料交易價格，并進一步分析制造商的最優(yōu)廢料處理策略。從供應鏈視角出發(fā)，李海燕等[6]基于委托代理理論，研究了廢棄物提供商與利用商之間的博弈模型，設計了基于用量激勵的交易合約機制。陳軍和楊影[7]通過構建政府與工業(yè)生態(tài)鏈上下游核心企業(yè)之間的博弈模型，研究了政府補貼對核心企業(yè)產(chǎn)品定價與副產(chǎn)品交易價格的影響。然而李海燕等，陳軍和楊影都忽略了副產(chǎn)品協(xié)同生產(chǎn)過程中上下游企業(yè)的議價能力，而本文在綜合考慮副產(chǎn)品協(xié)同生產(chǎn)和供應鏈成員存在議價能力的前提下，分析主產(chǎn)品的產(chǎn)量決策和廢料交易價格。

關于供應鏈環(huán)境下的納什討價還價模型，學者們進行了大量的研究。其中Bernstein和Marx[8]研究了由單一供應商和多個競爭零售商之間如何通過納什議價的方式進行供應鏈總體利潤的分配問題。Nagarajan和Bassok[9]研究了單個裝配制造商向多個供應商采購互補零部件并裝配成最終產(chǎn)品以滿足需求的分散供應鏈系統(tǒng)，同時考慮上游供應商可能組成聯(lián)盟的情形，研究結果表明，供應鏈的均衡結構是成員間相對議價能力的函數(shù)，同時當制造商的議價能力較低時，上游的供應商會形成穩(wěn)定的聯(lián)盟，而當其議價能力較高時，上游的供應商會保持獨立，這是制造商更偏好的結果。Guo和Iyer[10]在單個制造商和競爭型零售商的垂直結構下分析了成員間的多邊議價問題，研究結果表明當零售商的銷售價格差別較小時，制造商更傾向于選擇同時議價，而當銷售價格差異較大時，制造商更愿意選擇順序議價的方式。Feng和Lu[11-13]采用一般納什議價(GNB)的框架分析了競爭性供應鏈的外包決策和契約選擇。Hsu等[14]采用基于領導者的合作議價方法(LCB)分析了分散式采購和合作采購下的激勵問題。Basak[15]在納什議價的框架下比較了下游競爭性企業(yè)進行產(chǎn)量和價格決策的最優(yōu)利潤，研究結果表明，當最終產(chǎn)品存在替代關系時，產(chǎn)量競爭可以給零售商帶來較高的利潤，相反，當最終產(chǎn)品存在互補關系時，價格競爭會給最終產(chǎn)品生產(chǎn)者帶來較高的利潤。趙道致等[16]通過構建基于轉換成本的委托代理模型，研究了影響供應鏈成員議價能力的因素以及這些因素起作用的內在機制。張新鑫等[17]以中國醫(yī)藥市場為背景，研究了企業(yè)議價能力和集中采購效率對制藥企業(yè)集中參與意愿的影響。與上述研究不同的是，本文在副產(chǎn)品協(xié)同的背景下來研究上游制造商最優(yōu)產(chǎn)量決策以及廢料的最優(yōu)交易價格，并將供應鏈成員在協(xié)商議價時的保留利潤內生化，最后分析議價能力對成員最優(yōu)決策的影響。

2 模型描述與假設

考慮由環(huán)保型上游制造商和下游處理廠構成的兩級供應鏈結構。上游制造企業(yè)在期初投入Q單位的原材料進行產(chǎn)品A(稱之為主產(chǎn)品)的生產(chǎn)，產(chǎn)品生產(chǎn)完成之后在主產(chǎn)品市場上銷售。假定一單位的原材料可生產(chǎn)出一單位的主產(chǎn)品。同時在主產(chǎn)品生產(chǎn)的過程中會產(chǎn)生γQ單位的廢料(在基本模型中假定廢料的產(chǎn)出比例為確定的，考慮隨機產(chǎn)出比例并不會對本文的結論產(chǎn)生影響，詳見3.3節(jié))。鑒于廢料對環(huán)境的污染以及政府對環(huán)保的要求，制造商需對產(chǎn)生的廢料進行處理。常見的處理方式有兩種：一種是制造商自己采用傳統(tǒng)技術進行處理，每單位的處理成本為s；另外一種是制造商將廢料賣給具有技術許可的廢料處理廠進行處理，每單位廢料的銷售價格為w。處理廠通過對廢料進行加工生產(chǎn)出副產(chǎn)品B并在副產(chǎn)品市場上進行銷售。圖1描述了制造商與處理廠協(xié)同生產(chǎn)的供應鏈結構。

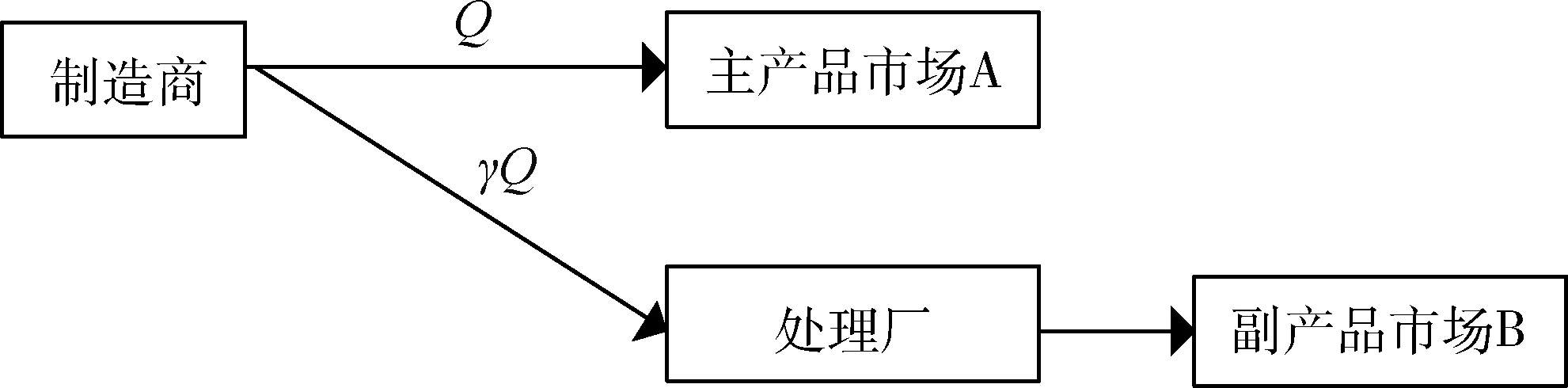
圖1 供應鏈結構

在現(xiàn)實中，廢料的交易價格往往是雙方(制造商和處理廠)通過議價(談判)的方式產(chǎn)生的。雙方的議價能力和保留利潤決定了最終的廢料交易價格。當議價成功時，制造商可從廢料交易中獲得額外收益，同時處理廠可將廢料加工生產(chǎn)成副產(chǎn)品B進行銷售從而獲取利潤。當議價失敗之后，制造商將自己進行廢料處理，這會對制造商產(chǎn)生處理成本且廢料不能轉化為副產(chǎn)品B，處理廠也無法獲取利潤。

不失一般性，我們假定主、副產(chǎn)品的市場需求函數(shù)為線性需求(如：Feng和Lu[11],Hsu等[14])，分別為P=a-bQ,P0=a0-b0Q0，在這里a(a0)表示主(副)產(chǎn)品產(chǎn)量為零時的最高價格(即消費者的保留價格)，b(b0)表示消費者對主(副)產(chǎn)品的產(chǎn)量敏感度。當議價成功時，處理廠將廢料從上游制造商處全部買回，最終的副產(chǎn)品以市場出清價格進行銷售。制造商和處理廠的產(chǎn)品生產(chǎn)成本分別為C和c0。

事件發(fā)生的順序如圖2所示。制造商在第一階段決定主產(chǎn)品的產(chǎn)量Q，同時在生產(chǎn)過程中會產(chǎn)生γQ單位的廢料；在第二階段，制造商和處理廠通過納什議價的方式?jīng)Q定廢料的交易價格w。議價完成之后，處理廠獲取廢料并對其進行加工生產(chǎn)出副產(chǎn)品，最終在副產(chǎn)品市場上以出清價格進行銷售。

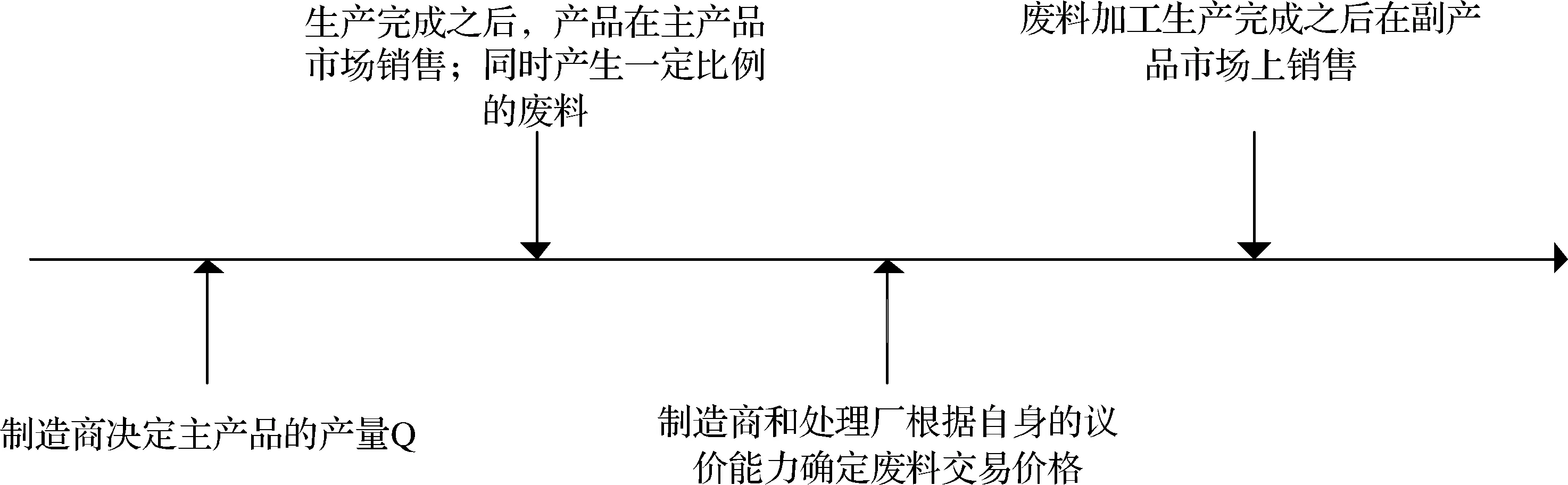
圖2 事件發(fā)生順序

3 模型分析

根據(jù)事件發(fā)生的順序，該問題可以轉化為兩階段的優(yōu)化決策。通過反向歸納的方法，首先分析第二階段，在給定制造商在第一階段的產(chǎn)量Q的前提下，制造商和處理廠在第二階段最優(yōu)交易價格的決策，然后分析制造商在第一階段的最優(yōu)產(chǎn)量決策。

3.1 最優(yōu)交易價格的決定

在該階段，給定制造商在第一階段主產(chǎn)品產(chǎn)量Q的前提下，制造商和處理廠通過議價決定廢料的最優(yōu)交易價格。為了分析最優(yōu)交易價格，我們首先給定制造商和處理廠在議價成功時的利潤以及議價失敗時的保留利潤。當議價成功時，廢料以w的價格銷售給處理廠，處理廠將廢料進行加工成副產(chǎn)品，以市場出清價格進行銷售。此時制造商和處理廠的利潤函數(shù)為Πm=(P-C)Q+wγQ,Πp=(P0-w-c0)γQ。

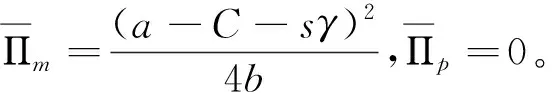
根據(jù)文獻[8-15]中，一般納什議價(GNB)的分析框架對納什產(chǎn)品(Nash Product)的定義,可以得到納什產(chǎn)品的利潤函數(shù)為

(1)

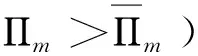
命題一：給定制造商在第一階段的最優(yōu)生產(chǎn)量Q時，制造商和處理廠之間關于廢料的最優(yōu)交易價格為：

w*(Q)=β(a0-c0-b0γQ)

由命題一可以看到，制造商同處理廠的之間副產(chǎn)品的交易價格取決于雙方的保留利潤、自身的議價能力以及相關的成本參數(shù)。特別的,當β=1時，上游制造商享有絕對的議價權，此時的最優(yōu)交易價格為w*(Q)=(a0-c0-b0γQ)，同時下游處理廠的利潤為零。以下推論給出了相關參數(shù)對最優(yōu)交易價格的影響。

推論一：在給定制造商最優(yōu)產(chǎn)量決策的前提下，第二階段的最優(yōu)交易價格有如下性質：

由推論一的結論可知，廢料的交易價格隨著制造商保留利潤的上升而增加，隨著自身議價能力的上升而增加。當制造商自身處理廢料的成本上升時，降低制造商的保留利潤，從而削弱其議價能力，最終使得交易價格隨著廢料處理成本的上升而下降。對于處理廠而言，副產(chǎn)品的市場容量上升，使得副產(chǎn)品的市場價格上升，此時的廢料交易價格也會隨之增加；而當副產(chǎn)品的生產(chǎn)成本上升時，處理廠的單位利潤下降，使得廢料的交易價格下降。

3.2 最優(yōu)生產(chǎn)量的決定

在本階段，制造商需決定主產(chǎn)品的最優(yōu)產(chǎn)量以最大化兩階段的收益。制造商在第一階段的利潤函數(shù)可表示為

Πm(Q)=[P(Q)-C]Q+wγQ

(2)

式(2)中的第一項表示制造商銷售主產(chǎn)品的利潤，第二項表示制造商銷售廢料的收益。優(yōu)化(2)式可得到命題二的結論。

命題二：制造商在第一階段關于主產(chǎn)品A的最優(yōu)產(chǎn)量、主產(chǎn)品的均衡銷售價格以及制造商和處理廠的最優(yōu)利潤分別為

由命題二的結論可知，制造商在第一階段的最優(yōu)產(chǎn)量決策與自身的議價能力和保留利潤無關。同時制造商的最優(yōu)利潤函數(shù)包含兩部分，一部分由自身的議價能力帶來的在整個供應鏈利潤中分享的利潤；另一部分是由保留利潤所帶來的收益。而處理廠的利潤中除了包含由自身議價能力所分享的利潤之外，還有由于制造商的保留利潤帶來的利潤損失。這主要是由于處理廠的保留利潤為零。

命題三：存在一點

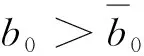
由命題三可知，制造商并不總是選擇將廢料給下游處理廠進行加工。當副產(chǎn)品的產(chǎn)量敏感度較大時，處理廠在同制造商議價時所獲得的利潤會下降，進而廢料交易價格下降。這就使得制造商在第一階段降低主產(chǎn)品的產(chǎn)量，從而獲得的利潤減少。因此，消費者對副產(chǎn)品產(chǎn)量較敏感時，制造商為了保持自身在主產(chǎn)品銷售中獲得較高的收益，會選擇自己處理廢料來獲取較高的利潤，此時處理廠無法獲取廢料來生產(chǎn)副產(chǎn)品。相反，當副產(chǎn)品的產(chǎn)量敏感度較小時，制造商更愿意通過與處理廠協(xié)商的方式確定均衡的廢料交易價格。

在均衡的狀態(tài)下，制造商的利潤隨著自身議價能力的上升而增加，而處理廠的利潤隨著制造商議價能力的上升而下降。這主要是由于當制造商在議價過程中的能力較強(或處于主導地位)時，通過議價會產(chǎn)生較高的廢料批發(fā)價格，制造商在廢料交易中所獲得收益會上升，最終會增加總體的利潤。同時，當制造商處于強勢地位(如β較大)時，處理廠在議價過程中就處于弱勢地位，最終形成的均衡交易價格就較高，進而處理廠所獲得收益就會下降。

3.3 隨機產(chǎn)出的情形

在該部分考慮當制造商產(chǎn)出比例隨機時，本文的結論是否依然穩(wěn)健。假定制造商的廢料隨機產(chǎn)出比例Υ的均值和方差分別為μ、σ2，其實現(xiàn)值為Υ=γ。事件發(fā)生順序與基本模型類似。需要說明的是，制造商在隨機產(chǎn)出比例實現(xiàn)之前決定生產(chǎn)量Qr,而廢料產(chǎn)出比例實現(xiàn)之后，制造商與處理廠協(xié)商廢料批發(fā)價格wr。

在第二階段，給定制造商產(chǎn)量Qr和隨機產(chǎn)出比例實現(xiàn)值γ的情況下，納什產(chǎn)品的利潤函數(shù)可表示為：

(3)

優(yōu)化(3)式，可得到：

w*r(Qr)=β(a0-c0-b0γQr)

在第一階段，制造商決定最優(yōu)的產(chǎn)量Q以最大化兩階段的利潤，此時制造商的利潤函數(shù)可表示為：

(4)

Pr*

從上式可以發(fā)現(xiàn)，在隨機產(chǎn)出比例的情況下，制造商的最優(yōu)產(chǎn)量以及供應量各成員的期望利潤函數(shù)與基本模型中確定產(chǎn)出的比例的結構類似。同時還可以得到，隨著廢料產(chǎn)出比例波動性的增加，制造商的產(chǎn)量下降，主產(chǎn)品和副產(chǎn)品的價格上升。而制造商和處理廠的期望利潤隨著產(chǎn)出波動性的增加而下降。

4 數(shù)值實驗

本節(jié)以確定性廢料產(chǎn)出為例，通過算例驗證本文的主要結論。首先給出制造商的最優(yōu)生產(chǎn)策略，其次說明副產(chǎn)品協(xié)同生產(chǎn)的價值。相關參數(shù)取值如下：顧客愿意支付的主產(chǎn)品、副產(chǎn)品的最高價格分別為a=200、a0=200,主產(chǎn)品、副產(chǎn)品的生產(chǎn)成本為C=20、c0=10,廢料處理成本為s=40,廢料產(chǎn)出比例為γ=0.9。

4.1 制造商的最優(yōu)廢料處理策略

分別取顧客對主產(chǎn)品、副產(chǎn)品的產(chǎn)量敏感度系數(shù)b、b0在區(qū)間[0,1]上變化。圖3描述了制造商處理廢料的最優(yōu)策略。其中區(qū)域“-”表示制造商將廢料給下游處理廠加工，區(qū)域“+”表示制造商自己處理產(chǎn)生的廢料。

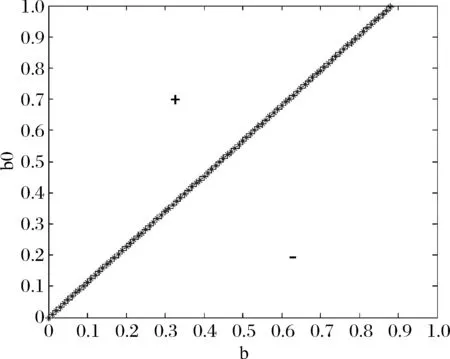
圖3 制造商廢料處理策略

從圖3中可以看到，制造商并不總是選擇將廢料給下游企業(yè)處理。具體而言，當顧客對主產(chǎn)品的產(chǎn)量敏感度較高或對副產(chǎn)品的產(chǎn)量敏感度較低的情形下，制造商更愿意將廢料給下游企業(yè)處理。這主要是由于制造商可從廢料銷售中獲得較高的收益。而當顧客對主產(chǎn)品的產(chǎn)量敏感度較低或對副產(chǎn)品的產(chǎn)量敏感度較高時，制造商更愿意自己來處理。這主要是由于制造商此時從廢料銷售中所獲得的收益較低，同時限制了主產(chǎn)品的生產(chǎn)量。由此可見，制造商和處理廠是一個共生的生產(chǎn)系統(tǒng)，雙方的決策相互影響。該結論對于實踐中制造企業(yè)選擇最優(yōu)的廢料處理方式具有借鑒意義。

4.2 副產(chǎn)品協(xié)同生產(chǎn)的價值

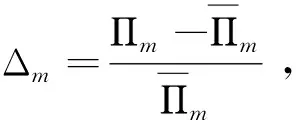
從圖4中可以看到，隨著制造商議價能力的增大，制造商通過將廢料給下游處理所獲得的價值就越高。這主要是由于較高的議價能力可以使制造商向處理廠收取較高的廢料交易價格，制造商在副產(chǎn)品協(xié)同生產(chǎn)中所獲得的收益就較高。因此可見，制造商在廢料交易過程中協(xié)商能力的大小決定了其在副產(chǎn)品協(xié)同生產(chǎn)中所獲取的價值大小。

5 結語

本文分析了供應鏈成員(上游主產(chǎn)品制造商和下游廢料處理廠)之間存在議價能力和副產(chǎn)品協(xié)同生產(chǎn)時的主產(chǎn)品的最優(yōu)產(chǎn)量決策以及均衡的廢料交易價格。研究結果表明，制造商并不總是選擇將廢料交由下游處理廠進行加工，這取決于顧客對副產(chǎn)品的產(chǎn)量敏感度。當消費者對副產(chǎn)品產(chǎn)量較敏感時，制造商會選擇自己處理廢料，此時相對于副產(chǎn)品協(xié)同生產(chǎn)而言，制造商可以獲得較高的利潤；相反，制造商會選擇給處理廠進行加工處理。此外，在議價成功時，制造商的均衡利潤隨著自身議價能力的上升而上升，而處理廠的均衡利潤下降。最后本文考慮廢料產(chǎn)出隨機的情形，發(fā)現(xiàn)本文的基本結論依然穩(wěn)健。本文的結論為實踐中制造企業(yè)如何選擇廢料處理方式以及廢料交易價格的確定提供了理論依據(jù)。需要說明的是，本文僅考慮主產(chǎn)品市場確定的情形，而在現(xiàn)實中企業(yè)所面臨的是顧客的多樣化隨機需求，因此分析在不確定需求環(huán)境下制造商的最優(yōu)產(chǎn)量決策是未來的重要研究方向。同時，本文僅研究了廢料價格通過議價方式確定，考慮其它的交易機制(如拍賣，競價)也是一個很有趣的研究問題。

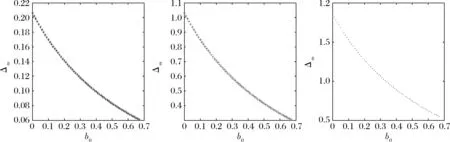
圖4 副產(chǎn)品協(xié)同生產(chǎn)的價值隨β的變化

附錄：

命題一的證明：將(1)式關于w分別求一階導和二階導可得

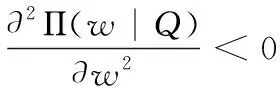
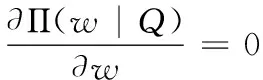
求解上式可得最優(yōu)的w*(Q)。從而命題一得證。

命題二的證明：將(2)式關于Q分別求一階導數(shù)和二階導數(shù)可得

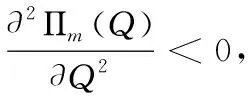
將Q*代入反需求函數(shù)P(Q)以及制造商和處理廠的利潤函數(shù)Πm(Q)、Πp(Q)，可得命題二的結論。從而命題二得證。

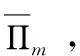
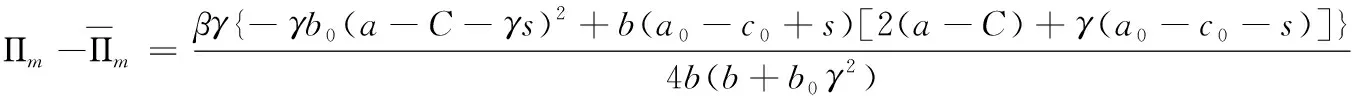
為便于表達，定義：

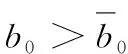
同時將最優(yōu)利潤函數(shù)Πm,Πp分別關于β求導可得：

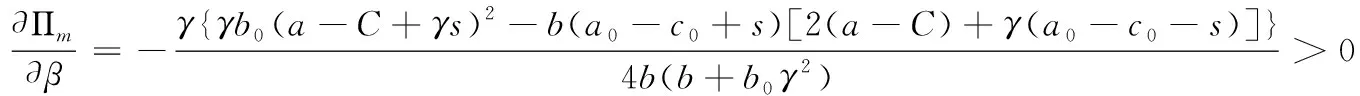
容易得出議價能力對利潤函數(shù)的影響。從而命題三得證。