翼型凹變在風電葉片氣動性能優化中的應用研究

唐格斯， 陳 建， 董雅君， 霍德豪， 趙 爽， 馬劍龍，4

（1. 內蒙古工業大學 電力學院， 內蒙古 呼和浩特 010080； 2. 營口市鋼鐵和鎂產業基地建設發展中心， 遼寧營口 115000； 3.內蒙古工業大學 能源與動力工程學院， 內蒙古 呼和浩特 010051； 4.內蒙古自治區高等學校可再生能源工程研究中心， 內蒙古 呼和浩特 010051）

0 引言

隨著風電機組設計的日益大型化以及其分散式應用向人類生存環境的靠近，對人類生存環境的影響越來越大，葉面流動分離惡化問題已成為葉片氣動性能設計成敗的關鍵制約[1]。因此，尋找并建立基于葉面流動分離有效控制的葉片氣動性能優化方法，已成為當前風電產業發展中亟待解決的重要課題。 翼型向翼面內側的結構凹曲變形（以下簡稱翼型凹變）作為防止和推遲流動分離發生的重要方法，近年來已成功應用于飛機機翼氣動性能的優化設計[2]，[3]。 然而，風電葉片結構較飛機機翼更為復雜，由此導致氣體繞流風電葉片時的非定常流動特征要比繞流機翼時復雜得多，因此，直接將相關成果應用于風電葉片氣動性能的優化設計不具備可靠性。 由此，相關研究工作的開展具有較好的背景和價值。

翼型凹變在風電葉片氣動性能優化中的應用屬于全新的課題，但是，翼型凹變屬于翼型優化設計范疇。 基于翼型優化的葉片氣動性能研究主要包括風電葉片專用翼型開發和先進設計方法開發兩個方面。 早期的葉片設計普遍采用航空翼型（如NACA 系列翼型），航空翼型具有最大升力系數高、最小阻力系數低等優點，對風電產業的早期發展起到了極大的推進作用。 然而，后續諸多實踐證實航空翼型對于高氣動性能風電葉片設計的適用性存在較多缺陷， 亟待風電葉片專用翼型的研發。自20 世紀80 年代中期開始，風電專用翼型的開發得到重視。至今，已形成了美國S 系列、荷蘭DU 系列、瑞典FFA-W 系列和丹麥Risφ系列翼型，為大、中、小型風電葉片的設計提供了基礎翼型數據[4]～[7]。 此外，研究人員還專門針對大型風電葉片開發了WQ-B 系列翼型[8]。

20 世紀末， 小型風電葉片的應用陡然升溫，相應專用翼型的開發也逐漸增多， 此時的研究工作不僅著力于專用翼型的開發， 同時特別關注葉片低速啟動問題和失速問題[9]～[11]。自2010 年起，建筑用風力機的開發得到重視， 至今已有多款專用翼型問世[12]。 隨著專用翼型的豐富，新翼型研發所需的長研發周期和高昂的研發費用使開發企業望而卻步。 因此，20 世紀末起至今，針對于已有翼型的氣動性能優化設計方法受到青睞， 期間風電市場的極速擴張和投資商不愿在技術引入費上的過多投入， 更是在極大程度上推動了相關問題的研究。 這一時期，研究人員不僅關注反設計法、失速延遲法、 遺傳算法等先進算法在翼型氣動性能優化中的應用， 同時對葉面的流動分離控制技術給予了特別的關注[13]～[16]。 國內外的相關研究人員分別在葉面流動分離的控制問題上開展了基礎性研究[17]。 但至今，除作者課題組外[18]，仍未見基于翼型凹變的葉片氣動性能優化方面的報道。

1 翼型凹變想法提出的理論基礎

圖1 為空氣繞流翼型時的流動特征。

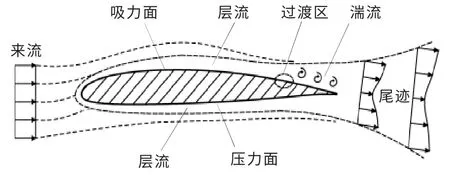
圖1 空氣繞流翼型時的流動特征Fig.1 Flow characteristics of air around airfoil

由圖1 可知，當空氣流經翼型表面時，在吸力面上靠近尾緣處往往存在由層流向紊流轉變的流動分離區。由流體力學基礎理論可知，層流邊界層在物體表面上產生的切向應力比紊流的要小得多，為了減小流動摩擦阻力，應使層流邊界層盡可能地長， 也就是使流動分離位置盡可能向下游推移，從而提升葉片的功率輸出。

加速流動比減速流動更容易使邊界層保持層流，為了實現流動分離點向下游的移動，本文嘗試在流動分離區域附近實現翼型向翼型面內側的結構凹變， 利用凹槽的抽吸作用使已經減速的流體得以加速， 從而防止或延后流動分離現象的發生。

2 翼型凹變形式的確定

圖2 為翼型凹變的實現過程。

圖2 翼型凹變的實現過程Fig.2 Implementation process of airfoil concave

以圖2（a）中翼型為例，假設流動分離常出現在M 處，則選該處為凹變中心。 考慮到翼型弦長顯著大于其最大厚度， 翼型凹變的幾何結構采用橢圓形，橢圓的長軸（A）為弦長（L）的7.2%、短軸（B）為弦長（L）的3.6%，并使A 與M 處原始翼型曲線相切， 本例中相切后A 與弦長間的夾角（α）為2.25°。凹變部分與非凹變部分間采用B 樣條曲線連接，具體過程如圖2（b）所示。

原始翼型葉片的結構如圖3（a）所示。 葉片為實心結構，長為700 mm，設有10 個特征翼型面，每個特征翼型面之間的葉片部分通過放樣實現，將原始翼型中的10 個特征翼型曲線執行相應的結構凹變， 并對各翼型曲線進行放樣后即可生成凹變翼型葉片[圖3（b）]。

圖3 葉片的生成Fig.3 Blade generation

3 翼型凹變位置和凹槽長度的確定

3.1 凹變位置和凹槽長度的預選

翼型凹變的中心嘗試選取在距離翼型前緣點0.7 倍、0.8 倍和0.9 倍L 處，凹槽的長度（由葉根指向葉尖）嘗試選取為350，420，700 mm，葉片代號及相應結構形式見表1。 翼型凹變位置和凹槽長度的最終選定需以葉片做功能力的大小為參考。

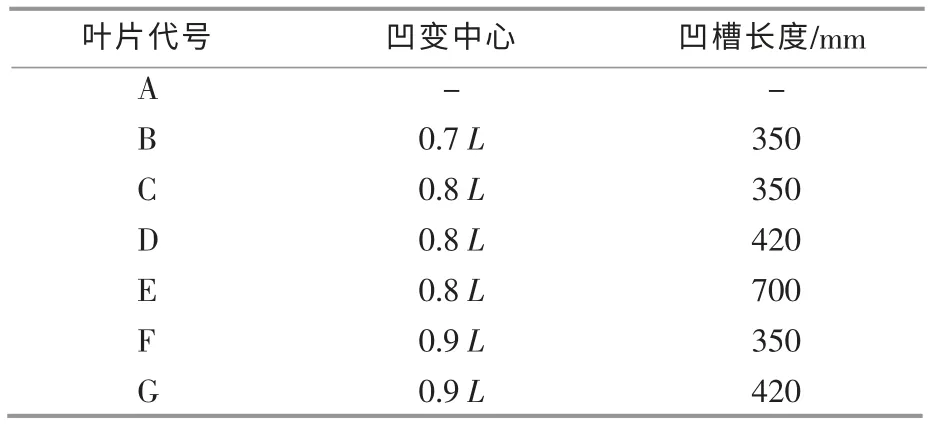
表1 葉片類型Table 1 Types of blades

3.2 計算模型

計算模型如圖4 所示。 該數學模型是依據內蒙古自治區新能源試驗示范基地的B1/K2 型低速風洞建立， 目的是利用相應的實驗數據檢驗數值仿真結果的可靠性。

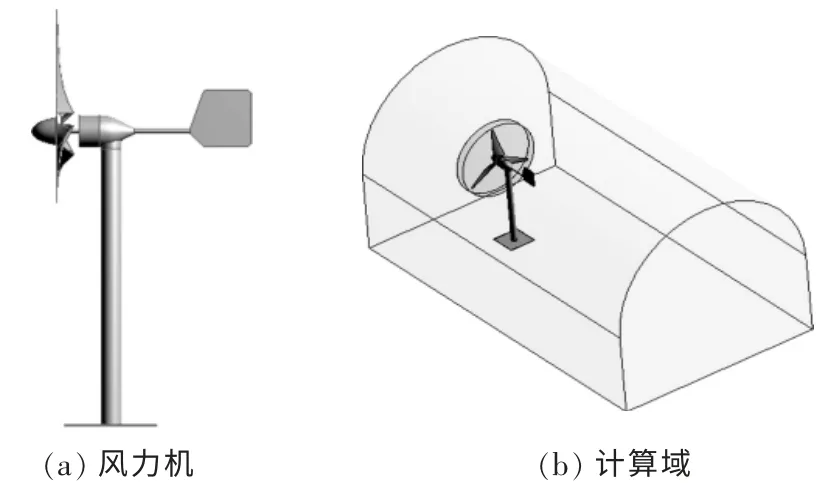
圖4 數值仿真模型Fig.4 Numerical simulation model

3.3 網格劃分

3.3.1 流場網格劃分

網格分為靜止域和旋轉域， 交界面間數據傳遞通過滑移網格實現，其控制方程如式（1）所示。

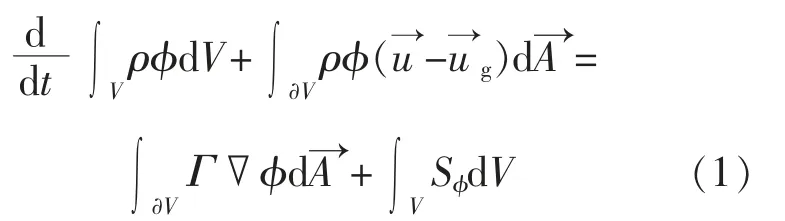
圖5 所示為計算域采用分區域加密。

圖5 網格的分區加密Fig.5 Partition encryption of mesh

3.3.2 結構場網格劃分

由于風力機葉片包含較多曲面， 葉片扭角較大的位置對網格劃分質量要求較高， 所以對葉片較薄處區域利用貼體網格進行加密。 計算域入口以速度作為邊界條件（選擇額定風速為8 m/s），出口以靜壓作為邊界條件（相對壓力設為0 Pa）。

計算域的壁面及地面設置為無滑移壁面，壁面的粗糙度為光滑壁面。 風力機的壁面設置為無滑移壁面，壁面粗糙度為光滑壁面。依據風力機實際測試條件，流體材料設為25 ℃的空氣，并為連續流體。

3.4 湍流模型及控制方程

3.4.1 湍流模型

由于所選算法須考慮湍流剪切應力， 且不會對湍流黏度產生過度預測， 同時考慮到計算的時間成本，因此，本文選用SST k-ω 模型開展計算。

3.4.2 控制方程

控制方程為

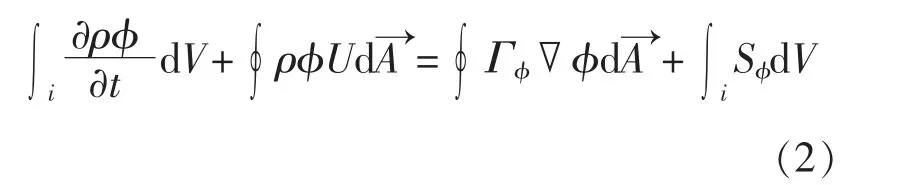
計算域中網格的每一個單元都是一個獨立控制體，式（2）能夠運用于每一個單元，這樣控制體方程可以表達為

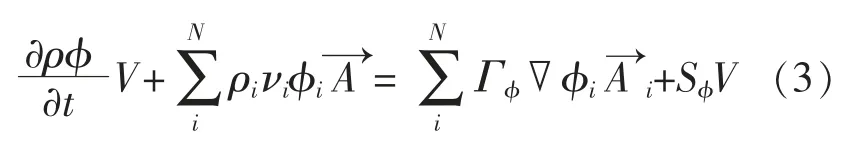
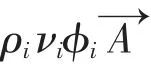
3.5 計算結果

在非穩態條件下利用SST k-w 算法開展計算。 以來流風速為8 m/s、葉尖速比為5 為例，7 類葉片氣動性能的數值計算結果如表2 所示。 由表2 可知，6 種翼型結構的凹變形式中，C 葉片的功率輸出提升效果更為顯著。 因此，以下開展C 葉片和A 葉片其它方面性能的對比。

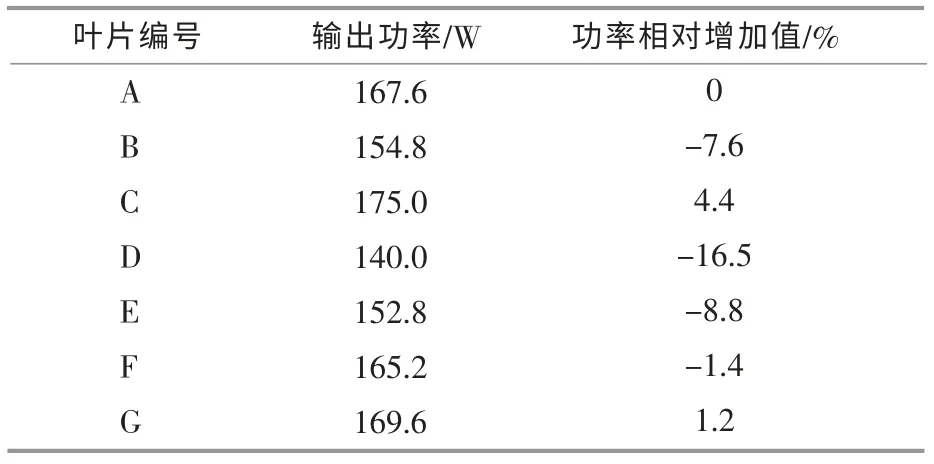
表2 不同凹變形式對葉片輸出功率的影響Table 2 Influence of different concave types on blade power output

4 翼型凹變對葉片氣動性能的影響

加工制作的A 類和C 類葉片如圖6（a）所示，測試風洞如圖6（b）所示。 風洞開口實驗段內徑為2 m，可提供0～20 m/s 的均勻來流。 發電機輸出信號由Fluke Norma5000 裝置采集， 其可實現電頻率、電壓、電流、電功率等多種發電機輸出參數的實時監測。 葉片的轉速可通過發電機輸出電頻率除以電極數間接獲得。

圖6 葉片和測試設備Fig.6 Blade and test device

4.1 測試結果與分析

為了考證不同工況時翼型凹變對葉片氣動性能改良的適應性， 分別在來流風速為5～8 m/s 和葉片轉速為400～650 r/min 時開展測試，結果如圖7 所示。由圖7 可知：翼型凹變對葉片氣動性能的提升效果不僅僅適用于額定工況，在其它工況時也有較理想的提升效果； 在來流風速為8 m/s、葉尖速比為5（對應葉片轉速為550 r/min）時，A，C葉片功率輸出的數值仿真結果相對于實驗值的相對誤差分別為6.2%和6.4%， 由此也證實了上述仿真結果的可靠性。 仿真值大于實驗值的原因為數值仿真為理想工況，沒有考慮葉片實際運行中的流動損失。

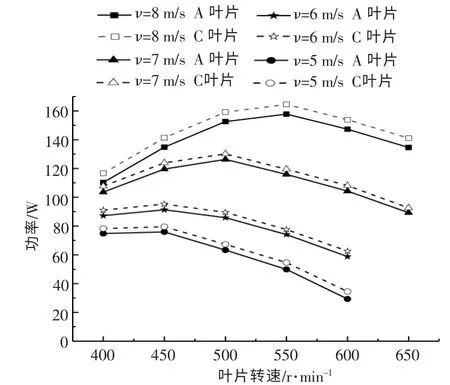
圖7 翼型結構凹變對葉片氣動性能的提升Fig.7 Effect of airfoil concave on the aerodynamic performance of blades

為進一步量化翼型凹變對葉片氣動性能影響的敏感性， 對同一工況時功率的增幅φp做如下定義：

式中：P1為原始翼型葉片功率；P2為凹變翼型葉片功率。

凹變對葉片氣動性能影響的敏感性如圖8所示。 由圖8 可知：當風速為7 m/s 時，翼型凹變對葉片氣動性能的增益最小；當風速為6 m/s 和8 m/s 時，增益值會有一定程度的增加；當風速為5 m/s 時，隨著葉片轉速的增加，翼型凹變對葉片氣動性能的增益效果會顯著增加；當風速為7 m/s和8 m/s 時，隨著葉片轉速的增大，由于翼型凹變導致的葉片氣動性能的增加量呈先減小后增大的規律；當來流風速為5 m/s 和6 m/s 時，增益值隨著葉片轉速的增大而增大。

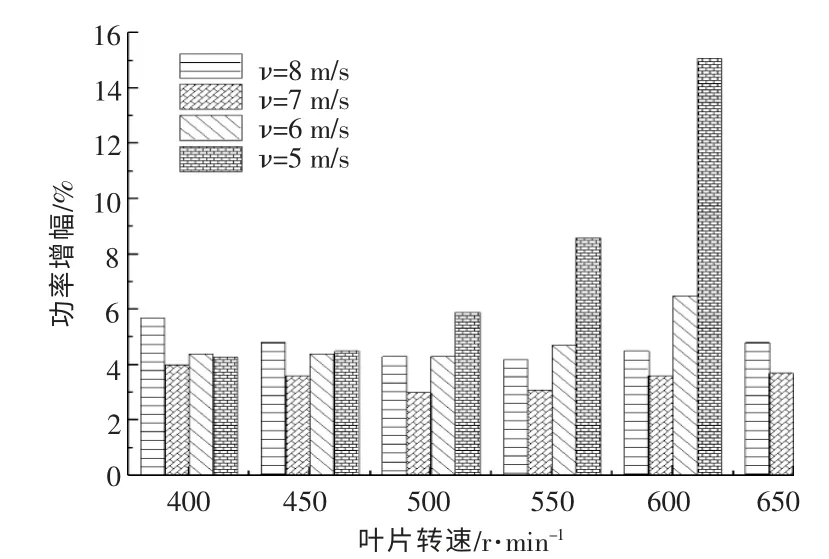
圖8 凹變對葉片氣動性能影響的敏感性Fig.8 Influencing sensitivity of the airfoil concave to the aerodynamic performance of blades

4.2 翼型凹變對葉片氣動性能影響的機理分析

為進一步探究翼型凹變對葉面流動影響的機理。 令葉片長度為R，考慮到C 葉片的凹槽分布于葉片葉展方向的0.15R～0.65 R（以葉根為起點）的范圍內， 將翼型面壓力分布的提取位置設在0.3R，0.4R，0.5R，0.6R 處（圖9），圖中1，2，3，4 截面分別對應上述4 個位置。

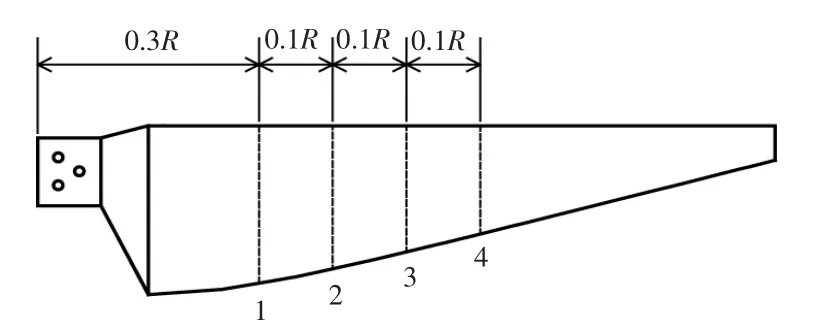
圖9 壓力數據的提取截面Fig.9 Extraction section of pressure data

仍以來流風速為8 m/s， 葉尖速比為5 為例，1～4 截面上的壓力分布如圖10 所示，圖中左側為原始翼型葉片，右側為凹變翼型葉片。

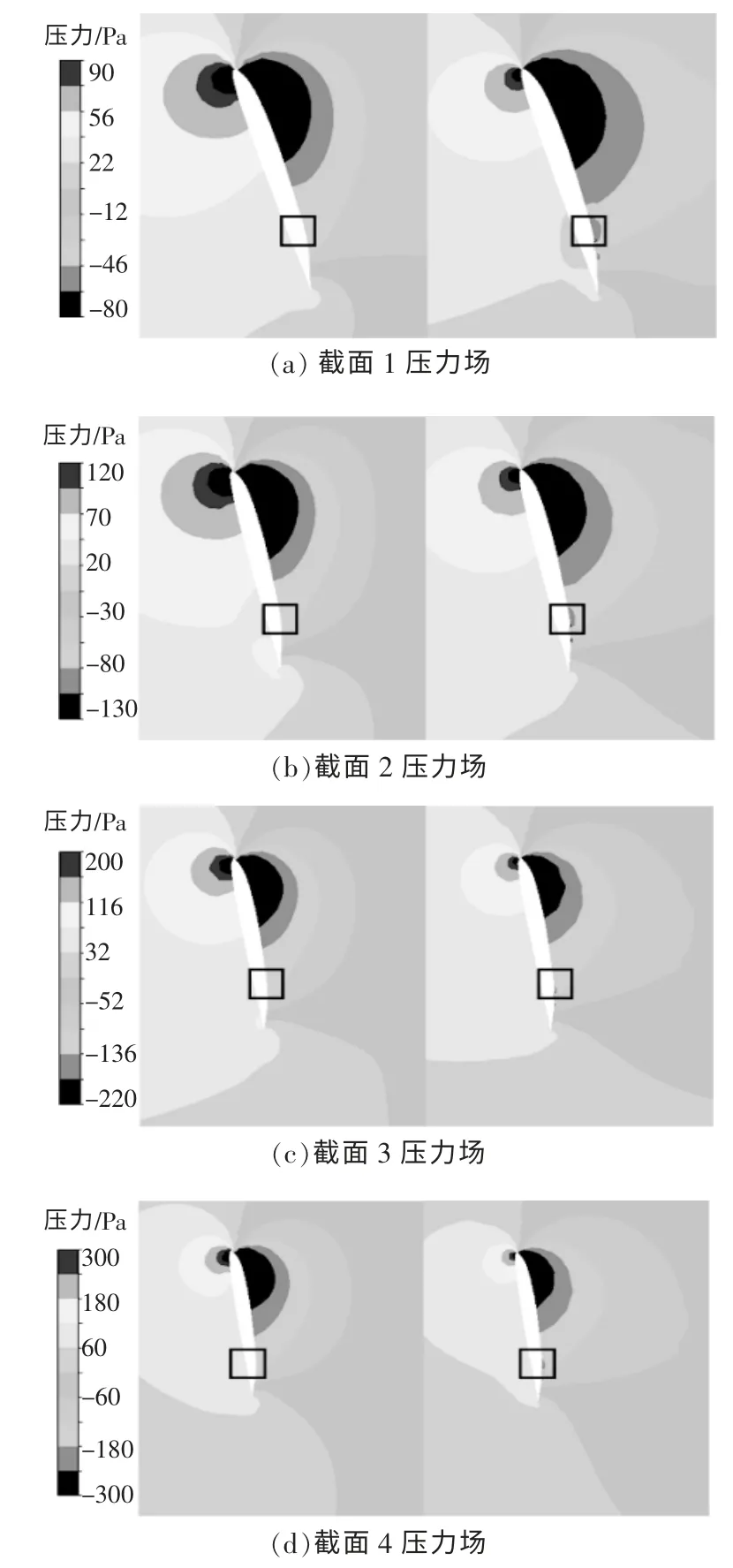
圖10 葉片不同位置處的壓力分布Fig.10 Pressure distribution at different locations of the blade

由圖10 可知：在A 葉片的0.8 倍弦長區域附近，確實存在明顯的壓力升高現象，不利于層流流動的保持；凹槽的出現會使附近壓力明顯降低，進而對流體流動產生明顯的局部壓力誘導效應，使流體產生加速流動。

由流體力學基本理論可知， 加速流動比減速流動更容易保持層流的流動狀態， 可使層流流動向紊流流動過渡的位置向后推移， 有效減小流態轉變誘發的流動阻力增加， 從而使葉片的氣動性能提升，這也是相同工況下C 葉片的功率輸出較A 葉片提升的原因。

5 結論

本文利用橢圓弧在葉片吸力面上實施了翼型凹變，通過凹變參數的合理選擇，可以實現對葉面流動分離的有益控制。就本文凹變樣例而言，可以得出以下結論。

①翼型凹變在不同工況（不同風速和葉片轉速）下對葉片做功能力的增益效果存在明顯差異。

②啟動風速至額定風速間， 翼型凹變對某一中間風速下葉片做功能力的增益效果最差。

③低風速時，隨著葉片轉速的增大，增益值變大。

④高風速時，隨著葉片轉速的增大，增益值呈先減小后增大的規律。