淺談量綱法推導物理公式的優勢
——以勻加速直線運動公式為例

●綦勝田 崔虹云 胡冰玉

一、學生學習量綱的必要性和可行性

（一）必要性

量綱學習的必要性主要體現在用數學方法解決物理問題的過程中。用數學方法解決物理問題先要定量分析物理公式中的物理量，也就是確定這些物理量的量綱，物理量的量綱確定后便可以將物理公式和數學函數密切的聯系起來①。但物理量的定量分析與簡單的數字化不同，物理量并不是簡單的數字，對于量化后物理量要認識其背后的物理含義，如理解加速度時要注意其數值的大小，表示的是物體單位時間內速度的改變量。所以物理公式與數學函數之間的關系需要量綱作為橋梁，因此不論是物理公式的定量分析或是物理問題的轉化都是建立在量綱的基礎上，由此可見物理量綱學習的必要性。

（二）可行性

往往在研究和檢驗復雜物理公式時才會分析其中物理量的量綱，但量綱是量化物理量的基礎，具有基礎性，對于簡單的物理量或公式同樣適用。高中學習的物理量和物理公式又都是簡單的，清晰的，學習并理解這些物理量的量綱相對來說也是容易的。并且在高中物理必修一已經涉及到量綱，在力學單位制這一節，該部分雖然沒有明確介紹量綱，但量綱就是這部分的知識來源。在2017年版《普通高中物理課程標準》中指出物理學科核心素養主要包含物理觀念、科學思維、科學探究和科學態度與責任。物理觀念的形成需要以物理視角看待身邊的實際問題，實際問題與物理公式或規律聯系需要學生對于物理量的準確理解，這就需要學生掌握量綱②。由此可見量綱的掌握既符合學生物理學習的需要，也符合物理觀念形成的需要。因此量綱的學習對于高中學生是可行的。

二、推導勻加速直線運動學公式的常見方法

一般來說在研究初速度勻加速直線運動中，位移，時間和加速度三者關系計算公式的推導是通過作圖的方式來獲得的。將物理量之間的關系即物理問題轉化為函數關系即數學問題，雖然這是物理學到數學的一種常見遷移，但在高中階段，這是首次用數學的方式解決物理問題。作圖法需要引導學生理解勻變速直線運動中V-T圖像各部分的物理意義，再將勻變速直線運動的位移轉化為函數圖像面積的求解③。這種將物理問題轉化為數學函數問題和面積的求解的方法，雖然是經典且常用的方法，但考慮到學生的初次接觸，思維和認知能力受到年齡的限制，直接的轉化略顯突兀。而量綱的學習可以幫助學生快速理解作圖法。教師可在問題轉化前給予學生提示或思路，而學生將量綱作為橋梁思考作圖法，教師再給予講解，使學生既看到作圖法解決物理問題的便捷，切實感受數學與物理結合的奇妙。

三、量綱法推導勻速直線運動的運動學公式

（一）量綱、基礎量、導出量、量綱式和量綱指數

量綱（dimension）即物理量的基本屬性。對于某一物理量的量綱，一般的表述方式是在該物理量字母前添加量綱英文縮寫前綴，如長度的量綱即為dimL④。使用量綱法推導物理公式首先需要明確基礎量和導出量。因為將物理量區分為基本量和導出量是量綱法研究物理學的基礎。物理量分為兩種,第一種是基礎量，由7個物理量構成，它們分別是長度L、質量M、時間T、電流強度I、溫度K，物質的量n和光強度J⑤。基礎量的特點是量綱式即為其本身，如長度L的量綱式為dimL=L。第二種是導出量，導出量是指由兩種或者兩種以上基礎量構成的物理量，并且目前物理學中所有的導出量都可以用基礎量導出。正因如此導出量都可以改寫為由基礎量組成的數學形式，這種數學形式就是量綱式。量綱式是指將導出量還原成基礎量的方程式。將物理公式中所有導出量還原為基礎量，再將乘除等運算關系改寫為相應的冪指數的。如對于任一導出量A可以得到如下量綱式的通式：

dimA=LαMβTγIδTεnζJη（1）

式中的每個基本量的指數α，β等稱為量綱指數。以此為基礎，可以寫出運動學中導出量速度v和加速度a的量綱式。速度v的量綱式由基礎量長度L和時間T組成，速度量綱指數α=1，γ=-1，不包含其他基礎量，則其余量綱指數為零。加速度a的量綱式由基礎量長度L時間和T的量綱組成，其量綱指數α=1，γ=-2，同樣不包含其他基礎量，其余量綱指數同為零。量綱式如下：

dimν=LT-1dima=LT-2（2）

（二）量綱法推導初速為零勻速加直線運動的運動學公式

因為物理公式不僅反映物理量之間的關系，同時反映等式兩端物理單位之間的關系，所以物理學公式的研究，可以在建立量綱后，通過物理公式的等式關系加以數學推導快速確定物理公式或者判斷公式是否正確，這種方法就是量綱法。量綱法首先需要確立量綱和物理公式的等式關系，再將各物理量改寫為量綱式帶入等式進行推導。如量綱法推導初速為零的勻速加速直線運動公式，首先需要確定影響位移x的物理量，通過生活經驗與邏輯分析發現，影響物體位移x大小的物理量包括加速度a和時間t，并且加速度a與時間t都與位移x呈正相關，以此建立等式關系，帶入各物理量的量綱式。等式關系即為位移x的量綱式等于比例常數k倍加速度a的量綱式與時間t的量綱式之積。經過數學推導得到兩個物理量的量綱指數，檢驗后完成基礎的物理公式推導。

確定影響位移的物理量，確定物理量之間的關系

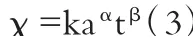
將公式中包含的物理量改寫為量綱式，k為比例常數

將（4）帶入關系式（3）中，整理得到推導式

通過由等式關系可得

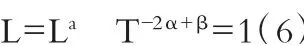
則有

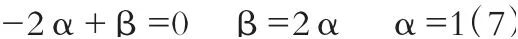
由此可推導出基礎的初速為零的勻加速直線運動運動學公式

四、總結

每個物理公式的函數形式無不透露著物理學與數學的對稱美。這種美需要以確定物理公式中每個物理量的量綱為基礎，只有確定量綱才能連接物理與數學。量化公式中的物理量確定其量綱是連接物理學與數學的基礎，同樣也是遷移并解決物理問題的重要一步。量綱法推導物理公式與常見的推導方式相比，將上述的推導過程適當加入教學中后，在問題轉化前給予學生提示或思路，而學生根據提示將量綱作為橋梁思考物理問題與數學問題的轉化，教師再給予講解，使學生水到渠成地理解作圖法，看到作圖法解決物理問題的便捷，切實感受數學與物理結合的奇妙。養》。]

注釋：

①梁燦彬,曹周鍵,陳陟陶.量綱分析簡介[J].大學物理,2017,36(12):1-5

②廖伯琴.普通高中物理課程標準(2017年版)要點解讀[J].物教學學,2020,42(02):2-5

③堵健忠,孫林偉.教會學生用作圖法破解高中物理學習障礙[J].湖南中學物理,2017,32(04):77-78

④談慶明.“量綱”一詞溯源[J].力學與實踐,2007(01):72

⑤談慶明.說說“量綱”和“量綱一”[J].力學與實踐,2009,31(01):107+103