例談幾何概念教學的動態化策略

【摘要】本文闡述運用動態化策略教學小學幾何概念的途徑，提出在動態化教學中挖掘幾何知識的本質，梳理幾何概念知識之間的關系，變式表征幾何概念等教學建議，讓空間關系更加清晰，幫助學生精準理解幾何概念的內涵，有效建構知識網絡。

【關鍵詞】圖形運動 動態課堂 概念本質

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2020）25-0114-02

新課標將空間觀念的發展作為一個核心概念明確提出來，并指出讓學生在幾何概念的學習過程中把握實物與幾何圖形相互之間的關系，以此發展學生的空間思維。基于此，筆者認為，在小學幾何概念教學中，教師要將物體和圖形的運動融入課堂，運用動態化策略將靜態的幾何圖形進行動態化處理，幫助學生在動態變化中獲得直觀的體驗，由此精準地把握圖形之間的空間關系，深刻理解幾何概念的本質特征，促進空間觀念的發展。

一、運用動態策略凸顯概念本質

在小學幾何概念教學中，小學生的思維以具體形象思維為主，容易被外部的顯性特征吸引，學習往往流于表面，對幾何概念的內隱性、抽象性等特征存在理解偏差。因此，教師可以借助動態化策略，讓隱性的概念特征顯性化，動態挖掘概念本質，促使學生精準理解幾何概念的本質內涵。

在教學部編版數學教材四年級上冊《平行與垂直》一課時，筆者發現，大部分學生能熟練背誦“平行”的定義，但在做練習時卻暴露出認知上的誤區，認為“不交叉就不相交”“相交就是交叉”，這說明學生對概念的理解還停留在外在表征上，沒有透過現象挖掘平行的概念的本質屬性，頭腦中也沒有建立動態的空間變化關系。因此，筆者運用動態化策略設計教學流程。首先，筆者從學生的已有知識經驗入手，帶領學生回顧學過的“圖形的平移和旋轉”，給學生出示一張格子圖，并引導學生展開動態想象：①格子圖上有一條直線a，想象一下，這條直線向下做平移運動，平移后的為直線b，請問直線b和直線a有怎樣的位置關系？②現在要將格子圖上的一條直線，繞著線上的某一個點旋轉，想象一下，旋轉后的直線和原來的直線有怎樣的位置關系？

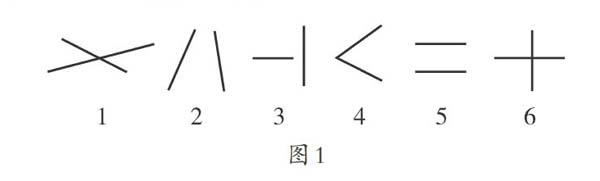
學生由此展開想象，在想象的過程中不但積累了直線運動中平移和旋轉的經驗，同時又對兩條直線在平面內的空間關系有了充分的體驗，為后續開展探究活動提供了豐富的素材。接著，筆者結合學生的已有活動經驗創設平移情境，激發學生挖掘平行線本質特征的積極性。筆者讓學生將兩條直線的位置關系畫出來，并有針對性地將學生的一部分作品展示出來（如圖1），讓學生在課堂上交流和討論：

觀察圖1，你能從中找出哪些是通過圖形平移得到的？哪些是通過圖形旋轉得到的？你能發現這兩種不同的移動方式形成的圖形位置關系有什么不同嗎？學生經過觀察比較之后發現，通過旋轉得到的兩條直線會相交，而通過平移得到的兩條直線不會相交。筆者繼續追問：為什么通過平移得到兩條直線不會相交呢？請說明理由。學生認為，直線平移之后，直線上的每個點都平移了，所以每一處對應點的距離都是相等的。緊接著，筆者讓學生動手操作，根據已有的平移的經驗畫出平行線。學生了經歷平移—平行—平移的認知過程，凸顯了平行這一概念中“平行線之間的距離處處相等”的隱性特征，由此在直觀體驗中獲得了深刻的理解。

以上教學環節，教師運用動態策略，幫助學生積累了直線（圖形）運動的經驗，讓學生充分感知平面內兩條直線的空間關系，同時又帶領學生將從平移中獲得的經驗遷移到平行線的認知中，加深了學生對平行概念的本質屬性的理解，再通過操作，利用本質特征直觀展示平移，由此獲得平行概念的內化。

二、運用動態策略拓展概念外延

在小學幾何概念教學中，學生往往會根據圖形的共有特征進行概念認知，學起來相對容易，但同時也給思維和認知帶來一定的局限性。這就需要教師運用動態策略，通過圖形的運動變化進行概念的表征，讓學生從變化中感悟不變，在圖形的動態變化中深入概念內涵，拓展概念的外延，建構系統化的知識結構。

在教學《三角形的高》這一內容時，如何讓學生認識直角三角形和鈍角三角形中的兩類特殊的高，這是教學的重點，也是難點。為了突破這一難點，筆者從運動變化的角度，運用動態策略設計課堂教學環節，帶領學生抓住銳角三角形的高這一概念的本質特征，將其遷移到直角三角形和鈍角三角形中。

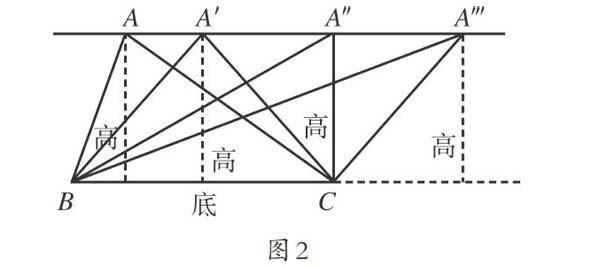
筆者給學生出示了一個平行線內的銳角三角形ABC，動態演示整個過程：以BC邊為底邊畫出三角形的高，然后過頂點A沿著平行線的一條直線向右平移，形成了一系列同底等高的三角形。（如圖2所示）

筆者引導學生觀察并思考：三角形什么發生了改變？什么沒有變？你從中發現了什么？學生發現，三角形的形狀在變化，但是底邊沒有變;高隨著頂點在移動，但高的長度不變。隨著向右移動頂點A，此時三角形的形狀發生了變化，銳角三角形變成了直角三角形，高的位置也發生了改變，高與直角邊重合了，此時直角邊不但是三角形的一條邊，同時也是三角形的高。接著，筆者繼續動態演示，將直角三角形的頂點A繼續向右平移，這時候學生發現，直角三角形改變了，變成了一個鈍角三角形，此時高不在三角形內，而在三角形的外面。通過觀察一系列的動態變化，筆者讓學生思考：想一想，高在三角形中的位置有什么不同？你怎么理解三角形的高？學生抓住銳角三角形、直角三角形、鈍角三角形這三類三角形中同底等高的聯系點，深刻認識到三角形的高就是從頂點向對邊所作的一條垂線段，高在不同的三角形中的位置也是不同的。銳角三角形的高在三角形內，直角三角形的高與直角邊重合，鈍角三角形的高在三角形的外面。

以上教學環節，教師借助動態策略，引導學生觀察思考，幫助學生拓寬了三角形的高的外延，突破了認知局限，進而讓學生在理解高的概念本質的同時培養了空間觀念。

三、運用動態策略梳理概念關系

在小學幾何概念教學中，每個概念都有獨特的屬性，同時也包含相互之間的密切關聯，因此，教師要運用動態策略幫助學生梳理概念之間的關系，幫助學生清晰地把握概念的本質，建構幾何概念的知識體系。

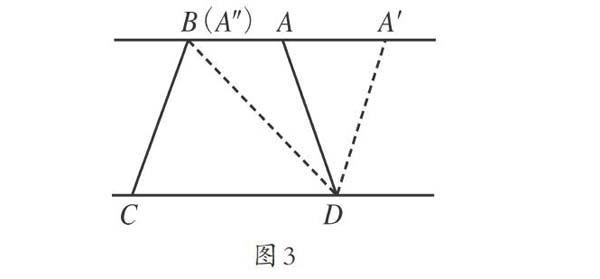
在學生學習了平面圖形的面積后，筆者運用動態化策略幫助學生梳理面積計算公式，讓學生借助幾何圖形的運動變化探究多邊形之間的特殊關系，從而構建平面圖形的面積知識網絡。筆者先讓學生思考平行四邊形和梯形之間的異同，學生確認平行四邊形是兩組對邊平行，梯形只有一組對邊平行。然后，筆者動態演示，沿著梯形上底的一個頂點平移，使其兩條腰也平行，轉化為平行四邊形。此時，學生直觀感知圖形之間的相互轉化關系，筆者引導學生觀察并思考：圖形運動中什么發生了變化？什么沒有變化？（如圖3所示）

通過觀察動態演示的過程，學生發現梯形的下底邊沒有變化，僅僅是上底邊發生改變。當梯形的上底邊與下底邊相等時，這個梯形就變成了一個上下底邊相等的特殊梯形——平行四邊形。

這個環節，筆者讓學生初步感知了平行四邊形與梯形的變與不變，由此梳理平行四邊形與梯形之間的相互關系。緊接著，筆者繼續動態演示，（如圖3所示）當A點逐漸靠近B點，上底的兩個頂點重合。學生發現，圖形又發生了改變，梯形變成了上底邊為零的特殊梯形，即三角形。

由此，學生在動態演示中，借助梯形在平行四邊形和三角形之間相互轉化，梳理了梯形的面積公式與平行四邊形的面積公式、三角形的面積公式之間的關系，使平面圖形的面積計算知識在動態梳理中更加系統化。接下來，筆者出示練習題，（如圖4所示）讓學生比較兩條平行線之間的平行四邊形、梯形、三角形的面積大小。

該練習題如果按照普通的解題方法，是要先假設高的值，然后運用面積計算公式計算各個圖形的面積，這樣進行比較，顯然是比較麻煩的。而通過動態演示，學生對平行四邊形、梯形、三角形的面積關系有了清晰的把握，他們一下子找到了問題解決的核心所在，學生認為，可以把三角形和平行四邊形都看作是特殊的梯形，一個是上底邊為零，一個是上、下底邊相等，在高相等的前提下，只要比較上下底邊之和的大小即可。由此，學生非常容易就得到了問題的答案。

以上環節，教師通過圖形的運動變化，以少統多，帶領學生系統梳理圖形面積計算公式，讓學生感悟圖形之間的相互轉化，認識到平行四邊形、三角形是特殊的梯形，由此深刻把握這三種圖形的概念本質，并將其綜合運用在練習中，讓學生在變中求解，在建構知識體系的同時，又發展了數學思維。

總之，在小學幾何概念教學中運用動態策略實施教學，能夠將抽象的數學概念與動態的具象結合起來，幫助學生深入理解運動變化下的幾何圖形，讓學生更加直觀地理解幾何概念，進而獲得圖形與幾何的概念建構經驗，從而建立空間觀念，促進學生更加深刻地理解幾何知識。

【參考文獻】

[1]王旭.小學數學幾何教學中培養學生空間概念的方式探尋[J].名師在線，2019（26）

[2]王海英.“圖形與幾何”的有效教學策略[J].江西教育，2016（21）

[3]管相娥.小學數學幾何教學方略探究[J].內蒙古教育，2017（22）

[4]許明堅.關注學習過程，讓“圖形與幾何”教學更有效[J].小學教學參考，2018（29）

作者簡介：吳萍（1976— ），女，廣西興業人，大學本科學歷，一級教師，研究方向為小學數學應用題教學研究。

（責編 林 劍）