基于刃邊法的模糊圖像復原

馬云 王成龍 時中榮

摘? 要：基于點擴散函數的模糊圖像復原是數字圖像處理領域的重要研究方向之一，其中點擴散函數的獲取一直是研究的一個熱點。現圍繞散射引起的圖像模糊開展研究，采用刃邊法采集圖像模糊核，以高斯函數為模型擬合出系統的點擴散函數，然后采用逆濾波完成圖像復原。仿真實驗表明，擬合出的點擴散函數較準確，圖像復原效果良好。

關鍵詞：點擴散函數;刃邊法;模糊;散射;圖像復原

0? ? 引言

在圖像采集時，對焦不準、運動、大氣擾動、散射等原因都會導致圖像發生退化，圖像清晰程度降低，甚至變得很模糊，丟失很多信息。比如在拍攝運動物體的時候會導致失真，此時獲得的圖片稱為運動模糊，需要對圖像進行重構才能變得清楚[1]。當光路中樹脂透鏡變形、損壞，或者光學元件在透鏡組中傾斜會導致成像發生變形，當透鏡設計有缺陷的時候也會引起枕形畸變或桶形畸變，這些誤差是經常會出現的。在水、霧、毛玻璃等物質的散射作用下，通過成像系統采集的圖像會發生退化，分辨率降低甚至發生嚴重模糊。比如在遙感衛星對地面采集圖像時，常因大氣的吸收、散射、放射導致圖像質量變差，甚至最終導致無法成像。導致圖像質量變差的主要原因是散射，大氣中的湍流或空氣中的水分會導致圖像模糊[2]。圖像復原的目的就是根據退化原因建立模型，對退化圖像進行處理，使其接近原始圖像。根據不同的成像模糊原因，需要采用不同的處理方法。

散射導致的圖像模糊可以看作是原始圖像由于成像系統傳遞函數存在缺陷導致了退化，從數學角度來說，成像就是原始圖像與模糊核發生卷積運算的結果，所以圖像的退化可以用式（1）的二維函數來描述[3]。

g（x，y）=f（x，y）×h（x，y）+n（x，y）? ? ?（1）

式中：g（x，y）表示退化圖像;f（x，y）表示原始圖像;h（x，y）表示點擴散函數;n（x，y）表示噪聲函數。

式（1）是退化過程在空域的數學描述，也可以用頻域表達式來描述，如式（2）所示。

G（x，y）=F（u，v）H（u，v）+N（u，v）? ? ? ? ?（2）

式中：G（x，y）、F（u，v）、H（u，v）和N（u，v）分別是退化圖像、原始圖像、點擴散函數和噪聲函數的傅里葉變換。

如果噪聲很小或者不考慮噪聲的影響，那么成像過程可以描述為式（3）。

g（x，y）=f（x，y）×h（x，y）? ? ? ? ? ? ? （3）

在圖像復原過程中，噪聲也是影響成像質量及復原效果的重要因素之一，是圖像處理中不可或缺的部分，有的圖像在復原過程中因為噪聲被放大導致圖像變得無法分辨。在復原算法中，通常采用逆濾波、維納濾波對圖像進行復原，逆濾波運算快捷，但是抗噪聲能力差，在處理含噪圖像時，更多會采用維納濾波。B. Knatarajan提出的基于SVD的圖像復原方法，能夠在復原圖像細節的同時很好地抑制噪聲或過濾噪聲，對于矩陣中的奇異值也能很好地解決。奇異值本身無論是出現在噪聲圖像還是估計的模糊核中，都會影響圖像的復原效果，而SVD復原方法在去除高斯噪聲并保護細節方面很有效[4-5]。

本文在仿真實驗中，主要工作圍繞點擴散函數的獲取開展，所以忽略噪聲因素的影響，采用式（3）對成像過程建模。

1? ? 點擴散函數的測量

在理想情況下，理想點光源經過一系列的光學系統后獲得圖像函數，成像系統或光學系統對理想點光源的脈沖響應稱為“點擴散函數”。一幅圖像可以看做許多點光源經過系統后在成像器件上的光場疊加，是卷積運算的過程，因此圖像復原就成為一個去卷積的運算過程。

在仿真實驗中，采用如圖1（a）所示的黑白方塊作為原始圖像，利用黑白邊界線在退化前后的變化，對點擴散函數進行估算。實際實驗中，對于采集到的彩色圖像可以采用單通道的方法進行處理，直接采用某個通道的灰度圖就可以完成圖像采集。依據散射原理和規律，在實驗中圖片的仿真退化采用高斯模糊，其中模糊核的大小為50×50（像素），標準偏差為5。

實驗中對原始圖像與高斯模糊核進行卷積運算后，圖像發生退化，特別是黑白分界線變得不再分明，如圖1（b）所示，實驗采用黑白交界線位置的數據進行測量和擬合。

獲得邊界像素灰度分布的數據后，對離散數據進行擬合，得到描述邊界灰度變化的連續分布函數，如圖2所示，其中連續曲線為擬合后的灰度分布函數，折線為原始數據。

2? ? 圖像復原實驗

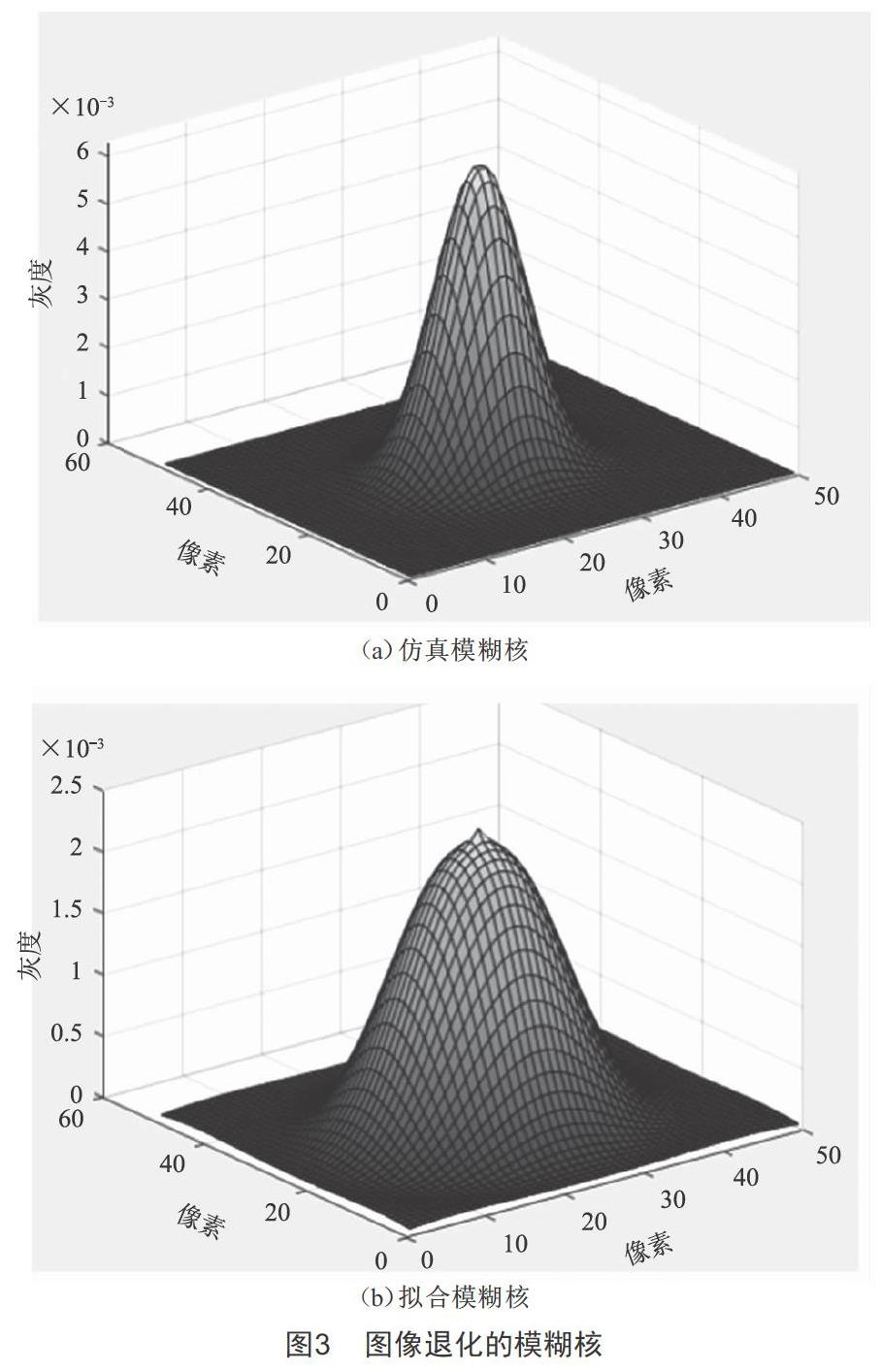
根據擬合獲得的線擴散函數，旋轉后估算出相應的PSF，如圖3所示。

從實驗擬合出來的點擴散函數可以看出，擬合的數據會因為模糊核對圖片的影響，導致點擴散函數中心不夠聚集，這是因為模糊核對圖像有平滑作用造成的。從圖像中也可以看出，擬合的點擴散函數中間有一個凸起的形狀，這是由于中心數據過少導致的擬合不平滑，最后在旋轉得到點擴散函數后，中間整體出現凸起，實驗中通過空域局部平滑濾波予以消除。

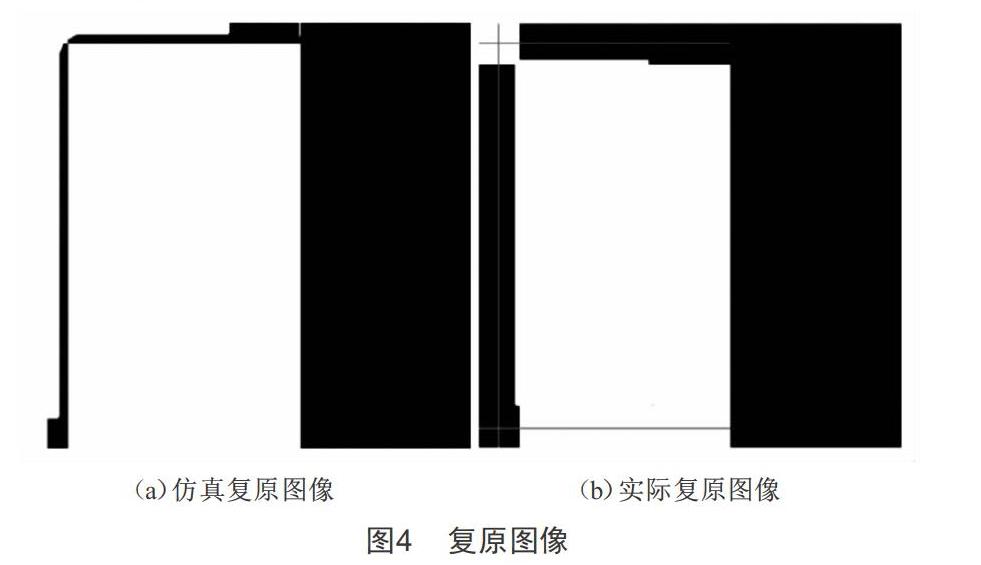
采用擬合的模糊核對退化圖像進行復原處理，結果如圖4所示。圖4（a）是利用仿真模糊核進行的復原處理，可以看出黑白界線分明，復原效果很好;圖4（b）采用測量數據擬合出的點擴散函數進行復原，黑白界線分明，復原效果良好，但邊緣有輕微失真。

3? ? 結語

本文采用刃邊法對模糊圖像的點擴散函數獲取進行了研究和實驗驗證，選擇黑白圖片對成像系統的點擴散函數進行標定，首先測量了退化圖像的線擴散離散分布數值，然后擬合出連續分布的線擴散函數，進而估算出系統點擴散函數，并進行了圖像復原實驗，結果表明，擬合出的點擴散函數較為準確，復原效果良好。

實驗中發現，在擬合邊緣數據的時候，距離邊緣較遠的數據要多選取一點，否則在擬合函數圖像的邊緣時會導致難以收斂。實驗中利用邊緣擴散函數經過變換得到點擴散函數，其中模糊核大小的估計對結果影響很大，實驗中采用了原圖像50×50像素的模糊核，在實際圖像處理中需要迭代計算出模糊核的分布區域。實驗結果出現的偏差除了模糊核誤差之外，求解過程中矩陣中數值為奇異值或接近奇異值，都會造成圖像處理的結果不理想。

[參考文獻]

[1] 孫偉.基于卷簾式快門的數字相機速度測量技術研究[D].長春：長春理工大學，2010.

[2] 朱瑜輝.基于大氣散射模型的霧霾天道路圖像清晰化[D].北京：北京工業大學，2010.

[3] DASH R，MAJHI B.Motion blur parameters estimation for image restoration[J].Optik-International Journal for Light and Electron Optics，2014，125（5）：1634-1640.

[4] 明文華.運動模糊圖像復原算法研究[D].合肥：安徽大學，2004.

[5] BUADES A，COLL B，MOREL J M.A non-local algorithm for image denoising[C]// Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR'05），2005：60-65.

收稿日期：2020-06-24

作者簡介：馬云（1979—），男，安徽六安人，碩士研究生，講師，研究方向：數字圖像處理與智能精密測量。