住宅內部特征對房價指數影響研究與思考
——以高層住宅樓層差異為例

□

在房地產價格統計調查中，新建住宅網簽數據是以小區為單位進行分類匯總，通過加權平均計算每月房價指數。然而在實際操作中發現，此種方法忽略了同一小區內不同樓幢、不同住宅類型、不同裝修標準甚至不同樓層間住宅的內部特征差異。本文以樓層差異對常州高層住宅的影響為例，嘗試找出住宅內部特征對房價影響的一般規律，嘗試找出研究類似問題的方法，為改進房價統計調查方法，進一步提高房價指數真實性提供參考。

|研究背景與意義

（一）新建商品住宅價格指數計算方法及問題

在現行房價調查方法制度中，房價指數計算方法是：先計算某一項目90 平方米及以下、90-144 平方米、144 平方米以上三個基本分類的環比指數，再將所有項目按照雙加權匯總計算全市三個基本分類的環比指數，然后對這三個分類環比指數加權匯總，計算出新建商品住宅環比指數。

然而同一項目同一分類月度成交內部特征差異，導致均價環比存在非市場波動因素。一是銷售房屋的位置、樓層、戶型、朝向、裝修程度等不同造成均價差異較大；二是部分特殊戶型引起均價變動較大，如某幢住宅頂層戶型價格普遍高于其他樓層，每平方價格高出上千元，這主要是由于頂層戶型為復式且贈送面積較大，造成均價波動較大。還有一些是由于普通住宅和排屋、別墅價格的差異引起；三是尾盤銷售，由于尾盤房源品質相對差些，加上回籠資金的需要，加大打折力度，造成同一樓盤環比價格差別。這些非市場因素一定程度上影響房價指數準確真實。

（二）樓層差異對價格影響研究現狀

國外住宅別墅和低層洋房占比很高，對樓層的研究和關注度不高。在利用特征價格法計算房價指數時，中外官方機構及學者通常將總樓層這一特征簡單歸類為高層、中層、低層，或者直接忽略，對于所在層的關注就更少了，通常只考慮是否為底層或頂層。而當前我國高層住宅占比較高，對樓層差異的相關研究就具有較大意義，同時可填補這一空白。

（三）樓層差異對價格影響研究意義

房地產是國民經濟的重要組成部分，對我國經濟發展起著舉足輕重的作用。在房住不炒的政策背景下，分析影響房價的因素，探究房價漲跌的原因對房地產市場的健康發展至關重要。真實可靠的房價指數是研究房價走勢的重要指標。研究樓層差異等住宅的內部特征對房價指數的影響可有效解決前文所述相關問題，進一步提高房價指數真實性，可靠性。

因住宅的內部特征較多，本文主要以研究樓層差異對常州高層住宅房價的影響為主，其研究思路和結果可應用于住宅其他內部特征。

研究樓層差異對房價影響不僅對現行房價統計調查制度有參考意義，還能在一定程度上對開發商住宅定價、房屋價值評估等提供標準，也可對消費者購房時樓層選擇提供參考。

（四）房價與樓層的一般關系

房地產價格是指建筑物連同其占用土地的價格，即房地產土地價格加建筑物價格，此價格是房地產市場運行和資源配置最重要的調節機制。影響房價的因素有經濟因素、社會因素、政治因素、住宅內部特征和環境因素。樓層是內在特征中的一個方面。

從供應端看，總高不同的住宅建筑其平均建筑成本有明顯差異，更高的樓層意味著更高的消防標準和安全標準，以及更多的水電等配套設施。客觀上，房屋價格因不同樓層視野、日照、通風、噪音等方面的差異而有所不同。從需求端看，不同樓層便利程度、空氣質量、堪輿（即風水）、電梯配比甚至樓層數字都會是購房者考慮的因素，從而對房價產生一定影響。橫向比較，關于樓層的消費偏好各個國家甚至相同國家的不同地區和城市因文化和風俗習慣等的差異都有很大的差別。

|實證研究

（一）指標選擇與數據來源

國家相關規定將10 層及10 層以上住宅定義為高層住宅。因10 層以下的住宅數據量小、且樓層差距對價格影響更為復雜，難以量化，故暫不做研究。

為了保證數據可靠性和可得性，盡可能保證數據完整，本文在2019年9 月到2020 年2 月常州市（不含溧陽）新建商品住宅（不含保障房）成交網簽備案數據中隨機抽取了5040 條成交記錄。每條成交記錄的均價記為p1，數據按照相同項目相同樓棟相同戶型和面積進行匯總計算平均價格記為p2。因各個樓盤之間甚至不同樓棟之間價格差異較大，因此引入了兩個均價的比值字段記為pr。pr 值的含義即為單套住宅均價占相同住宅不同樓層均價的比值，其值越大代表此套住宅價格相對其他樓層價格越高。需要說明的是，在數據匯總時，并不是所有項目樓棟的全部樓層都有成交，所以在選擇數據時剔除了部分成交記錄較少的樓棟。對于樓層，因為不同樓棟總層數不同，所以研究所在層數的絕對數對價格的影響在不同總層數的樓棟之間不具可比性。因此本文引入了相對位置的概念，相對位置包括在整棟樓中的樓層位置以及相對中間樓層的位置。樓棟的總層數記為zcs，所在層數記為szcs，所在層的相對位置即所在層數與總層數的比值記為cswz，距離中間樓層距離（計算方法為所在層數與二分之一總層數的差取絕對值然后除以二分之一總層數）記為zjwz。為研究特殊樓層，同時引入四個虛擬變量：1 樓、4 樓、18 樓、頂樓，分別記為F、F4、F18、FN，若符合樓層條件賦值為1，否則為0。表1 為數據導入STATA/SE 15.0后簡單的數據描述。

（二）初步觀察與分析

首先我們利用STATA 軟件繪制各變量的矩陣散點圖，觀察各個變量兩兩之間的關系，如圖1 所示。通過觀察發現pr 和cswz 兩個變量有正相關的線性關系，pr 和zjwz 兩個變量可能存在負相關的線性關系。其余變量除有直接邏輯關系之外沒有明顯線性關系。這也和我們的常識基本吻合，即高層住宅越高層越貴，或者高層住宅越靠近中間層越貴。接下來用一元線性回歸的方法具體研究。

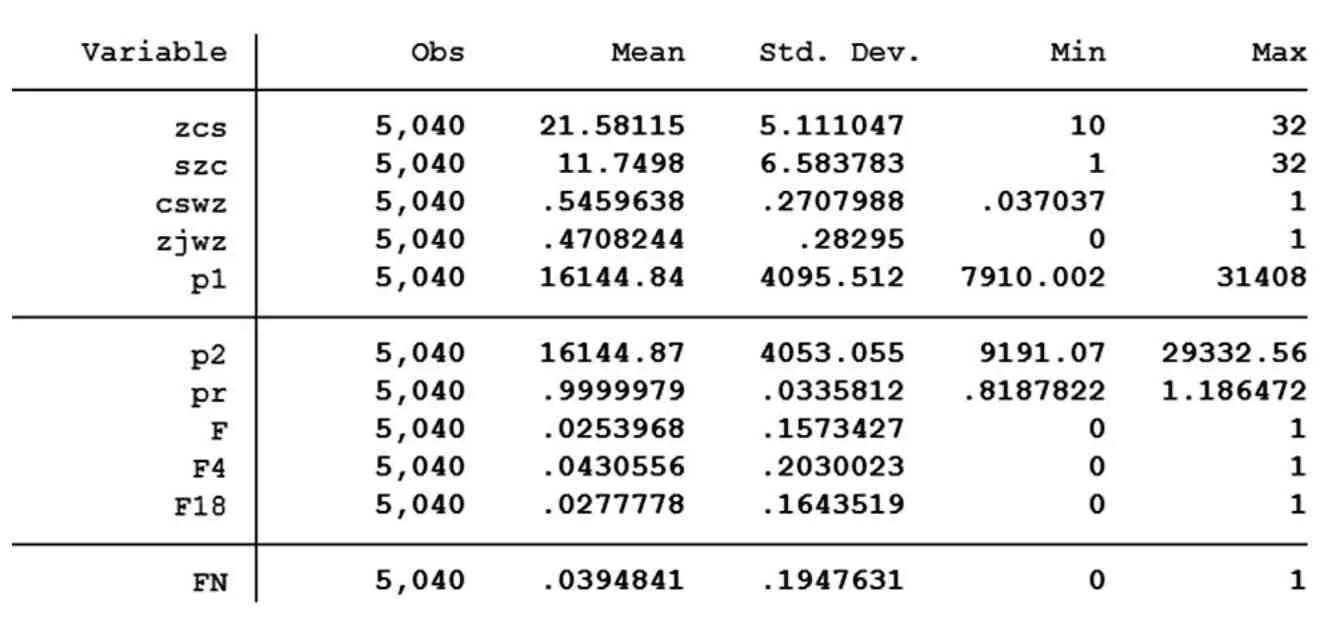
表1 各變量的數據描述

（三）做一元線性回歸

利用STATA 軟件分別對pr 和cswz、pr 和zjwz 兩組數據做一元線性回歸，所得結果如表2 和表3 所示，cswz 系數符號為正代表相對價格高低與樓層高低呈正相關，P 值小于0.05 拒絕了原假設，代表整個方程是可信的。

再來看pr 和zjwz 變量回歸分析的結果，zjwz 變量系數符號為負表示離中間樓層越遠價格越低，P 值同樣小于0.05。但R2值偏小且遠遠小于pr 和cswz 變量回歸分析的R2值，擬合優度較低。

通過以上的簡單分析，我們基本可以采信pr 與cswz 呈線性正相關的模型，即 pr=0.0725593cswz +0.9603831。其現實意義可簡單解釋為樓層越高相對價格越高。

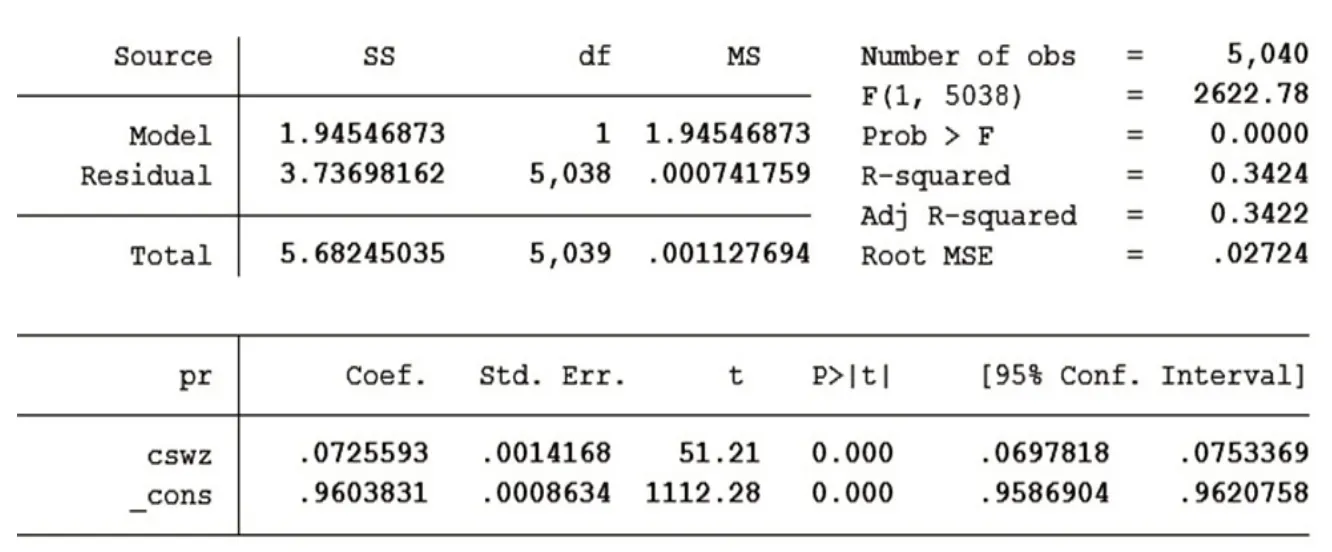
表2 變量pr和cswz一元線性回歸分析結果

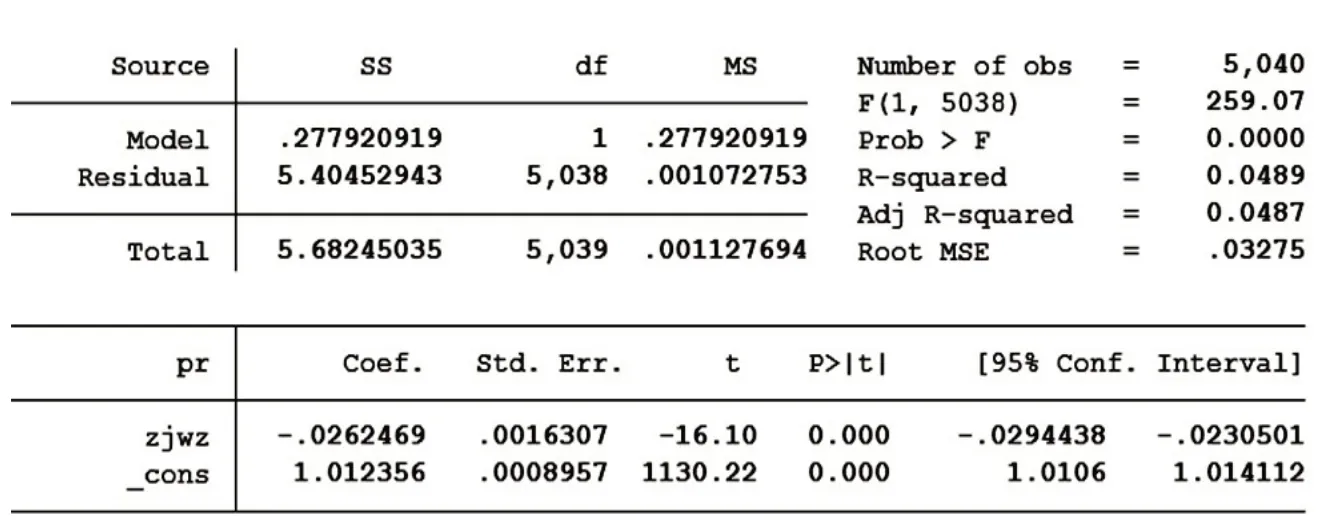
表3 變量pr和zjwz一元線性回歸分析結果

（四）分析首層和頂層對價格的影響

圖1 各變量的矩陣散點圖

我們注意到圖1 中首層和頂層有明顯的偏低或偏高的數據，因此，我們借助前文的結果引入F 和FN 兩個虛擬變量做多元線性回歸分析。結果如表4：

結果顯示，F 和FN 的系數符號均為負，代表首層和頂層均對房價有負面影響。同時我們注意到整個方程的調整的R2值為0.5130，相對0.3422 有了明顯的提高，證明引入兩個變量后方程的擬合優度更高。

（五）分析特殊樓層對房價的影響

為了研究特殊數字樓層對房價的影響，我們以4 樓和18 樓為例，進一步引入兩個虛擬變量F4 和F18 進行研究。需要注意的是，18 樓有可能同時是頂樓。多元線性回歸結果如表5：

與表4 的結果類似，F4、F18 變量系數的符號同樣為負，證明4 樓和18樓對房價同樣有負面影響。調整后的R2值進一步增大，擬合優度優于前式。

（六）實證分析結果

通過以上分析，結合實地走訪調研的情況，我們可以得到以下結論：

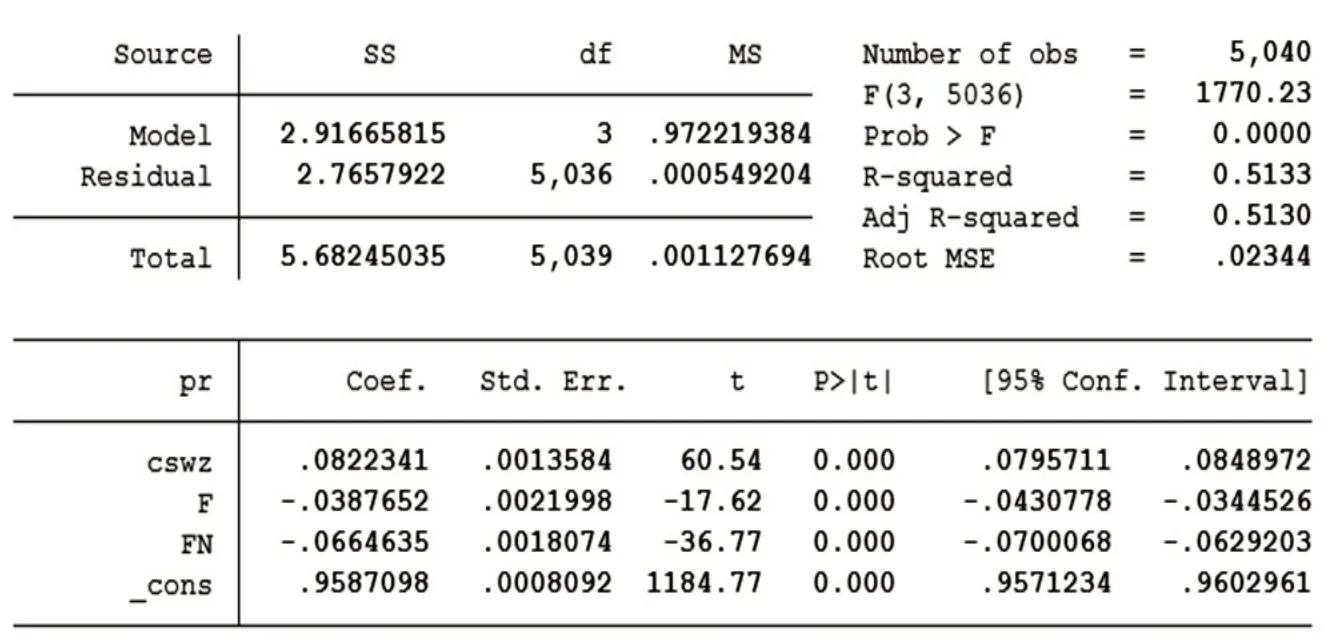
表4 變量pr、cswz、F、FN線性回歸分析結果

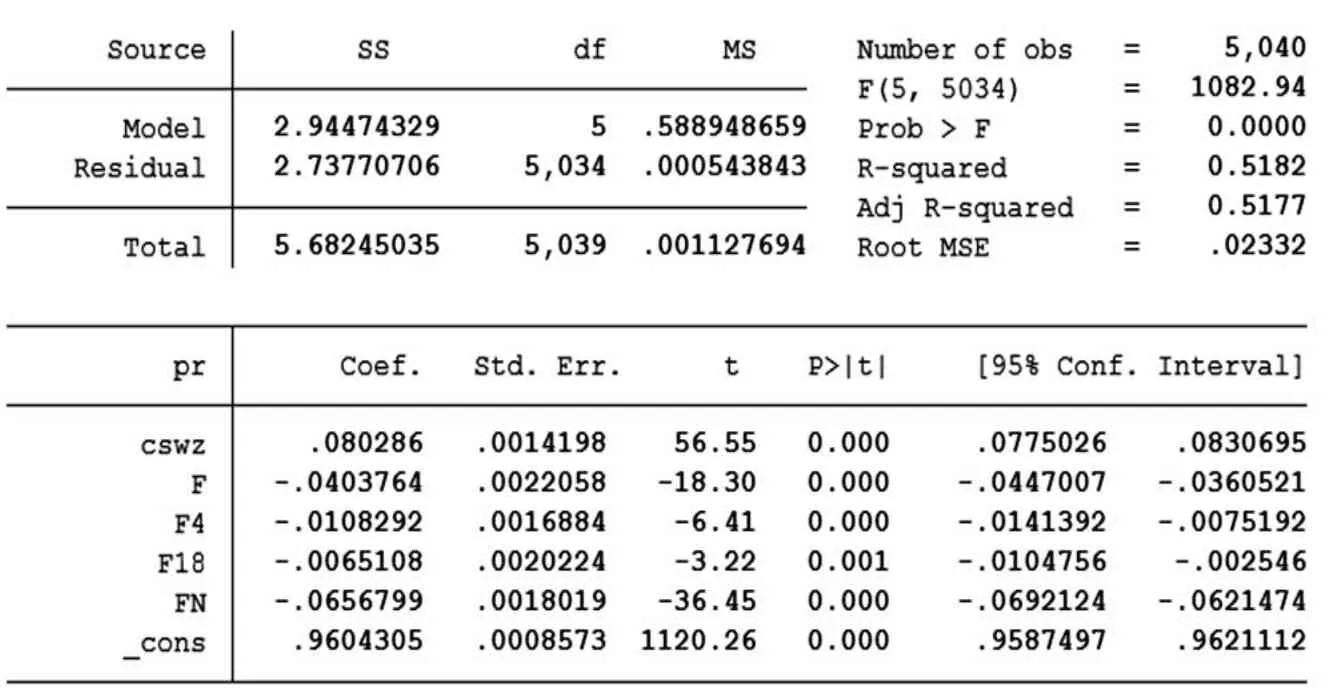
表5 變量pr、cswz、F、F4、F18、FN線性回歸分析結果

在其他條件相同時，房價與所在樓層數呈較強的正相關，與距離中間層的距離呈較弱的負相關。同時首層和頂層會顯著拉低住宅價格，一些特殊樓層也會對價格產生一定負面影響。

在圖1 中，一些首層和頂層呈現異常高價。結合之前的實地調研，分析可能的結果是部分首層會贈送庭院，頂層送閣樓或者樓頂使用權，導致價格較高。

在表1 的數據描述中，可以發現首層的頻數占比明顯低于本應該相等的4 樓成交數占比。原因一方面是一樓相對的銷售周期會比較長，通常會比普通樓層長數周甚至數月，導致在數據提取和篩選時沒有包含部分跨統計周期的備案數據，另一方面是部分開發商會將傳統意義的一樓建為車庫或其他設施導致一樓相對數量少。

根據表5 的結果我們可以得到樓層位置與相對價格的一般關系：pr=0.080286cswz -0.0403764F -0.0108292F4 -0.0065108F18 -0.0656799FN+0.9604305。取極值得到pr 最大最小值的比值為112.75%，也就是說因樓層差異相同住宅價格平均最大相差12.75%。此結果基本接近實地調研的真實情況。這說明，在樣本較少的極端情況下，單個項目價格的環比指數可能會偏離正常值12.75%。

|相關思考和探索

（一）結合數據分析和實際工作經驗，高層住宅首層和頂層等劣勢樓層交易周期相對較長，通常會跨不同統計周期。而此類住宅的價格通常明顯低于同幢住宅平均價格，在現行房價調查制度下，會在一定程度上拉低房價指數。建議可以采用加權或者剔除的方法消除特殊樓層對指數的影響。

（二）以項目為最小單位分類匯總新房網簽數據直接忽略了項目內部特征的差異，而這些差異足以影響房價指數的準確性。可以此文的相關結論和模型為基礎，采用對相應樓層的住宅賦予不同權數等方法優化房價指數計算方法。

（三）擴展到住宅其他內部特征，可以采用加權平均和特征價格法相結合的方式計算指數。即總的加權平均的計算方法不變，但在項目內部，采用特征價格法的思路，將項目內部的各個特征賦予不同的系數或權數。比如裝修標準，將同項目內不同裝修標準的住宅賦予不同的權數參與指數計算。以此類推，用特征價格法計算各項目的指數，再加權平均計算總指數。