動力災害過程中錨桿支護的極限承載能力數值模擬研究

魏明堯，張守文

(1.中國礦業大學 礦山互聯網應用技術國家地方聯合工程實驗室，江蘇 徐州 221008；2.廣州市城市規劃勘測設計研究院，廣東 廣州 510060)

瑞士、加拿大、澳大利亞和南非等地的一些金屬礦山已經開采到地下1 000 m，甚至達3 000 m，我國煤礦開采也逐漸進入1 000 m以下的深部環境[1]。深部環境下，巷道在高地應力(含上覆巖層自重應力、構造應力和采動應力)的作用下，巷道本身變形量較大，而且地震、大面積頂板垮落、頂板斷裂和爆破對其產生更強烈的動力擾動，造成圍巖嚴重變形破壞，巷道片幫冒頂頻率和強度增大，致使圍巖承載結構失穩破壞，極易發生毀滅性的沖擊地壓災害[2]。由于錨桿支護具有經濟、有效等特點，目前已成為煤礦巷道支護體系中的主要形式。隨著深部開采的增加，越來越發現錨桿缺乏對動力擾動環境下巷道的支護能力[3]。沖擊地壓、放炮和頂板垮落等引發的動態應力擾動造成錨桿應力集中，可能導致錨桿鋼材料屈服和錨固端破壞，最終致使錨桿失效[1]。由于礦井開采深度逐漸加大，近10年采煤巷道支護成本增加了1.4倍，而且實踐表明40%～80%的深井巷道需要翻修[4]。隨著地下工程向深部延伸，深部巷道受動壓影響產生嚴重破壞、維護困難、沖擊(巖爆)事故頻發、支護效果差等問題逐漸突出，外部動力擾動是導致圍巖破壞和支護失效的主要因素之一[5]。而在深部巷道錨桿支護措施中受深部應力環境影響，存在錨桿損壞嚴重、支護成本較高、巷道反復整修、支護效果不佳等問題。而工程中采用的錨桿支護理論仍是基于靜態應力環境的，對錨桿支護與圍巖形成的支護體系抵御動力擾動的能力以及強沖擊下支護體系的極限承載能力等動力問題未進行深入研究，而這些是保證深部巷道穩定亟需解決的問題。

盧愛紅等[6]利用LS-DYNA軟件模擬了不同圍巖條件下動態擾動誘發巷道發生失穩破裂的過程。Burget 等[7]和 Zhu等[8]分別采用相似物理模擬和數值模擬方法研究了沖擊地壓發生的過程和動力擾動引發的破壞結果。深部受擾動圍巖的穩定性控制是深部巷道維護的主要問題，也是目前研究的重要內容[9]。Littlejohn等[10]測量并評估了Wales的Penmaenbach 隧道的6.025 m直徑錨索受到近距離爆炸的影響。Haile等[11]監測了受模擬地震波源影響的錨桿支護間圍巖的動態反應，發現質點峰值速度(peak particle velocity, PPV)隨測點與支護距離的增加而增加，對于特定環境下的巷道存在一個造成巖體損傷的最小PPV值。Tannant等[12]檢查了兩個不同礦區中近距離爆破對錨桿端部的反應，并測量了錨桿軸向應變和巷道壁面質點速度，建立了一維有限差分模型，研究錨桿的應變和巖石表面的動態位移。理論研究方面，康紅普等[13]分析了采動應力場與支護應力場的關系，認為采動應力越強烈，對支護系統的要求也越高，動壓巷道支護體受力明顯大于靜壓巷道，需要采用高強度、高剛度且具有足夠延伸率的支護系統。張明光[14]分析了近距離煤層開采擾動下破碎頂板支護系統，提出增加支護系統預應力的方法來提高頂板穩定性。Mckenzie[15]總體調查和評價了Big Bell礦采用的可屈服錨桿抵抗沖擊地壓災害的情況，并對支護方式和支護順序進行了優化設計。Ortlepp等[16]對實施不同的和類似的支護設計原則的隧道進行了簡要調查，提出一些在深部支護設計過程中有用的準則和經驗。另外，大量學者通過數值模擬軟件對動載作用的錨桿結構動態響應規律進行了研究。St-Pierre等[17]基于實驗研究提出一種錨桿的動態模擬模型，結果發現錨桿有兩種能量吸收機制，分別是錨固端在樹脂內的滑移和錨桿的塑性位移。薛亞東等[18]采用FLAC軟件，對回采巷道錨桿(端錨和全錨)施加地震波擾動，模擬得出錨桿軸力隨動載作用時間的變化規律，同時發現錨桿安裝角對軸力的動載響應有很大影響。Ansell[19]開發了一種全新的吸能型錨桿，并在實驗室測量了其動力吸收能力。

本研究采用FLAC3D軟件對深部支護巷道動態應力波擾動過程進行數值模擬，并對錨桿支護體系的動態反應進行監測。通過在模型中施加特定強度的動態壓縮波，檢測錨桿受力數據和圍巖位移等數據，得到錨桿支護體系下的應力演化特征、支護體系的動力擾動響應及其穩定性特征，并分析支護體系的承載能力與巷道圍巖變形破壞的耦合關系；同時模擬不同動力擾動大小及方向、地應力環境條件下的影響。針對工程現場難以測量圍巖內部煤巖體及錨桿的變形規律的問題，本研究采用數值模擬方法反映巷道支護系統的物理過程，其結果為深入研究及優化深部巷道支護體系設計提供依據。

1 計算模型的建立

建立尺寸為50 m×50 m×50 m的幾何模型，總單元個數為10 612。巷道為拱形斷面巷道，寬4.0 m，高4.0 m；巷道頂底板和兩幫采用全長樹脂錨固錨桿支護，錨桿長5 m，間距為1.5 m，頂板布置3根，兩幫及底板各布置2根，巷道形狀和錨桿分布的斷面如圖1所示。在模型中距離巷道壁不同距離設置監測點，如圖1中所示的A、B、C、D和E點，與巷道壁的距離分別為0.5、2、4、6和8 m。

圖1 模型布置和動力加載示意圖

為了考慮深部巖體應力峰后特性，模型采用彈塑性本構模型并進行峰后應變軟化，煤層巷道的體積模量為10 GPa，剪切模量為3 GPa，抗拉強度為1 MPa，粘聚力為0.8 MPa，摩擦角為23°，其巖性軟化參數采用文獻[20]的參數，如表1所示。由于沖擊災害發生時間極短且毀滅性極強，造成監測設備毀壞，目前仍無法獲得災害發生時應力及應變的定量值，因此將沖擊災害發生簡化為應力波擾動。邊界條件設置如圖1，右邊界和底邊界為位移約束，上邊界為加載面，施加固定荷載，在左邊界施加動態變化的壓縮應力，模擬動力波擾動。分別設定上邊界荷載為15、20、25和30 MPa，模擬采深為600、800、1 000和1 200 m下的應力環境。力學阻尼選用瑞利阻尼形式，其中最小臨界阻尼比為0.005，最小中心頻率為50 Hz。邊界條件設置為靜態邊界。擾動應力波形取載荷波形中為諧波的一段，峰值強度取100 MPa[6, 21]。模型中錨桿的彈性模量為40 GPa，屈服荷載為110 kN，并且在模型中使用fish語言編寫判斷錨桿位移是否達到屈服極限的程序，如果錨桿達到屈服，則刪除此錨桿單元[22]。

表1 應變軟化模型參數表[20]

2 深部巷道圍巖動態破壞規律分析

2.1 動態破壞過程

壓縮應力波會造成巷道圍巖的應力分布發生變化，圖2是巷道圍巖受沖擊擾動過程中最大主應力的時空分布規律。圖2(a)為沖擊前的圍巖應力分布，由于開采造成的應力轉移，最大主應力呈環形分布，最大應力為29 MPa，距離巷道壁8 m，此時巷道壁變形極小。圖2(b)為動載作用時間為0.005 s的應力分布圖，在加載初期沖擊擾動未傳播至巷道位置時影響較小。當傳播時間為0.01 s時，沖擊擾動到達巷道位置，由于巷道的阻礙，應力波峰值分別轉移至巷道上方和下方，此時最大應力峰值為47 MPa，峰值區距離巷道6 m左右。圖2(d)為0.015 s時的應力分布，沖擊擾動分別在巷道頂底板中傳播，應力峰值逐步減小，降低為42 MPa。在0.02 s之后，由于沖擊擾動為壓縮波，傳播時在其后方形成拉伸應力區，如圖3,同樣也引發后續較小的壓縮波。當沖擊擾動后(如圖2(g)和圖2(h))，巷道圍巖被大量破壞，應力峰值轉移向深部，造成巷道嚴重變形。

圖2 擾動傳播過程中最大主應力分布圖

圖3是不同監測點處的應力和位移曲線。從圖3(a)可以看出測點距離巷道越近，其應力值越小，測點擾動前應力分別為0.6、7、13.7、21.5和26 MPa，說明越靠近巷道，圍巖破壞越嚴重，應力值也越低。隨時間增加，擾動沖擊波經過測點時應力值迅速上升，距離左幫2～6 m位置的平均升高幅度達43%～67%。應力波擾動過后測點的應力下降，同時沖擊波過后形成的拉伸波與原巖應力疊加致使測點產生較低的應力值，之后應力恢復原狀，但由于距離巷道較近處的圍巖損傷破壞嚴重，受到沖擊擾動后圍巖破壞加劇，應力明顯降低。圖3(b)為不同監測點的位移曲線。可以看出，在沖擊擾動前，位移基本平緩；受擾動影響后，位移逐漸增大，且距離巷道越近，增加幅度越大；距離巷道0.5 m處位移最大為0.2 m，增加幅度為54%。

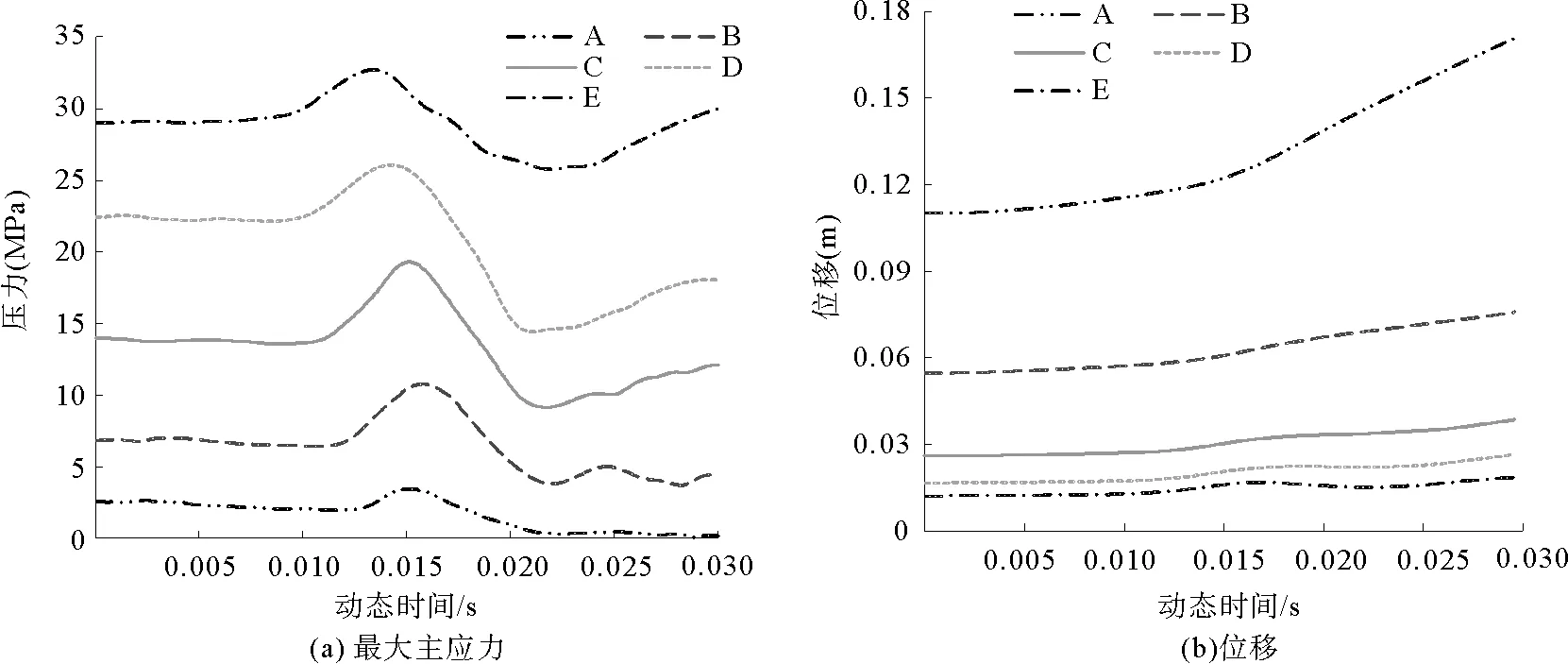
圖3 不同測點的最大主應力和位移的變化曲線(分布為測點A, B, C, D和E)

動力擾動造成巷道圍巖大量破壞，引起圍巖的大變形。圖4為巷道圍巖位移和速度云圖，圖中箭頭為位移向量，剪頭方向代表圍巖的位移方向，長度代表位移大小。可以看出，沖擊破壞后巷道最大位移在左側墻，底角處嚴重變形，最大位移為0.595 m，這是由于在沖擊壓縮過程中墻腳位置的剪切力較大，超過了剪切強度而發生剝落。同時底板發生拱起，形成底鼓，這是深部巷道破壞的特點。圖4(b)為擾動后巷道圍巖位移速度云圖，可以看出左側圍巖的位移速度較大，最大速度達25 m/s，足以導致大范圍的巖塊彈射，更嚴重的可以導致沖擊地壓發生。由于沖擊波入射到自由表面反射會形成拉伸波，這些反射回來的拉伸波將與入射壓縮波的后續部分相互作用，造成圍巖積聚大量動能，滿足斷裂準則后圍巖會發生彈射。沖擊擾動后巷道斷面嚴重變形，與原截面對比，發現巷道截面積縮小20.6%，說明沖擊擾動對巷道破壞嚴重。

圖4 擾動后巷道圍巖位移和速度分布圖

2.2 錨桿軸力動態響應及失效分析

動力擾動對錨桿軸力也產生重要影響。圖5為巷道左邊的一個錨桿單元的軸向應力隨時間的變化曲線。發現隨著圍巖的變形，錨桿工作阻力以線彈性增長到最大值，錨桿進入理想塑性狀態，并平穩保持在最大工作阻力上。當沖擊擾動傳播至錨桿時，錨桿軸力緩緩上升，達到錨桿單元的最大抗拉強度后，錨桿單元失效，軸向應力瞬間下降，此時錨桿單元完全失去支護能力。

圖5 錨桿單元軸向應力隨動載作用時間變化曲線

擾動過程中錨桿失效數量隨時間增長而不斷增加，圖6為沖擊擾動過程中統計的錨桿單元失效個數。錨桿單元失效首先發生在0.020 s，0.020與0.022 s之間失效數為8個，0.028～0.030 s間沖擊應力波到達巷道位置，錨桿單元失效個數高達27個。當0.04 s時總破壞單元個數為154個，占總單元數的39%，此時錨桿已完全失去支護能力。因此在強沖擊擾動作用下，深部巷道的錨固效果不很明顯，除非采取特殊的技術措施。

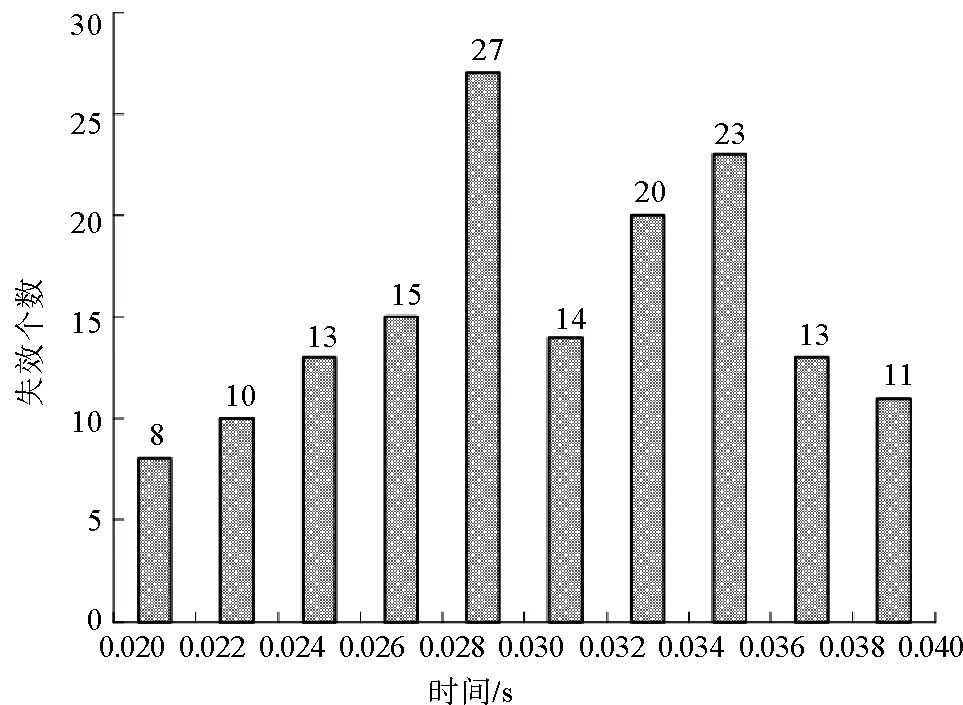
圖6 錨桿單元在單位時間間隔內失效個數統計圖

2.3 擾動強度對巷道沖擊破壞影響

沖擊強度的大小是決定巷道破壞程度的主要因素，不同強度的擾動對錨桿承載能力的作用不同。為研究錨桿的極限承載能力，需要對不同擾動強度下的錨桿響應進行分析。較小動力擾動時，普通支護足夠抵御動力破壞，巷道受影響較小，如小級別礦震一般不會對巷道支護造成嚴重破壞。而普通錨桿支護體系不足以抵御強動力擾動，造成巷道斷面大變形，甚至造成巷道完全封閉。沖擊地壓災害發生時能量極大，為了研究錨桿支護體系抵御強動力沖擊的能力，根據煤巖體的三軸抗壓強度將峰值擾動強度分別設定為10、50、100和200 MPa，進行4種動力擾動過程的模擬[6]。圖7為擾動過程中圍巖最大位移曲線。在10 MPa的動力擾動下，圍巖位移變化緩慢，在0.3 s時的最大位移0.25 m，僅比動力擾動前增加0.08 m。隨著擾動強度增大，位移量明顯變大，可以看出擾動強度為200 MPa時造成了巷道很大位移，在0.3 s時最大位移達到了0.67 m，是擾動前位移量的4倍，而且巷道變形嚴重，其截面積比擾動前減小25%。

圖7 不同擾動強度下巷道圍巖最大變形量曲線

通過對不同擾動強度下的錨桿總失效數目進行統計，得到圖8所示擾動過程中錨桿的總失效數目規律，在10和50 MPa的較低的擾動強度下，錨桿單元基本都處于其抗拉強度范圍內，錨桿損壞數目較少。當高強度擾動時，錨桿損壞數目眾多，最高占總錨桿單元的35%。而且錨桿破壞數目與擾動強度非線性增加，高強度的擾動造成更嚴重的錨桿破壞和圍巖變形。

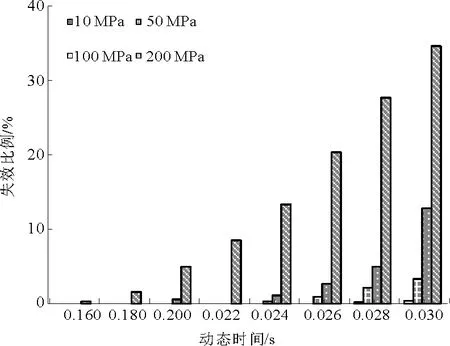
圖8 不同擾動強度下巷道錨桿隨時間的破壞比例

綜合分析錨桿支護體系對不同強度擾動的抵御能力，可以判定50 MPa以下的擾動對巷道支護影響較小，不會造成嚴重的巷道變形。高于50 MPa的擾動，圍巖和支護體系受損嚴重，不能達到支護的要求，而且隨著擾動強度增加，造成的破壞更加嚴重。

2.4 擾動方向對巷道沖擊破壞影響

深部地下工程中，動力擾動源位置不確定，對巷道不同方向產生沖擊破壞，為確定巷道錨桿的布置方案，需研究不同方向對巷道圍巖破壞區域定位。圖9為不同沖擊源位置造成的巷道圍巖位移向量圖，其中圖9(a)中沖擊源位于底板，圖9(b)中沖擊源位于頂板。當擾動源位于巷道下部時，巷道底板受影響嚴重，造成墻角和底板嚴重鼓起，兩幫變形較小。當擾動源位于巷道上部時，巷道上表面位移量變形范圍最大，位移量高達0.58 m，由位移向量可以看出，巷道頂部向下塌陷，造成巷道斷面嚴重變形，兩幫變形較小。對比不同位置擾動源的破壞作用，發現距離擾動源位置較近處圍巖受損最嚴重，造成的位移也最大，越遠離擾動源受其影響越小。

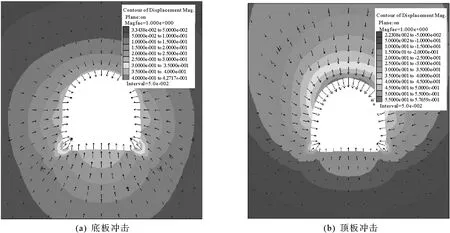
圖9 不同沖擊源位置對巷道破壞的位移向量圖

2.5 開采深度對巷道破壞影響

開采深度增加時，巷道圍巖將承受更高的地應力環境，造成圍巖的穩定性降低，支護難度和成本增加。圖10為600、800、1 000和1 200 m采深下沖擊擾動圍巖位移曲線。可以看出較小采深下，圍巖位移較小，沖擊擾動后變形幅度不明顯。當采深超過1 000 m后，圍巖變形大于0.2 m，沖擊擾動后圍巖破壞較嚴重，位移增加幅度明顯大于小采深環境，在采深為1 200 m時，最大位移為0.45 m，其中沖擊擾動產生的變形增加幅度為80%，此時巷道變形及破壞范圍遠遠大于小采深。采深增加也造成錨桿失效數量的增加，圖11為不同采深錨桿受載破壞個數。在淺部條件下，沖擊擾動造成的錨桿失效較少，當采深超過1 000 m后，錨桿失效個數將超過總數的50%，錨桿支護體系受到嚴重破壞。由于模型設定垂直應力和水平應力相同，而在自然環境中水平應力約為2倍的垂直應力，所以臨界采深會更低，資料顯示在800 m深度巷道破壞加劇，某些地區甚至在500～600 m時就發生嚴重破壞[23-24]。

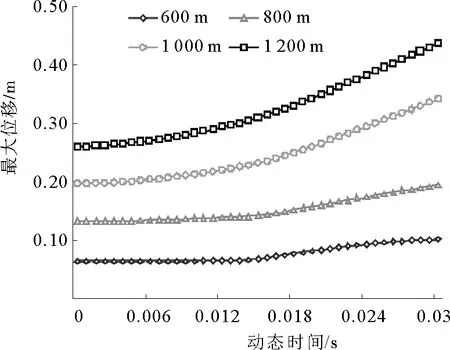
圖10 不同開采深度下位移變化曲線

圖11 不同開采深度下錨桿單元破壞比例

3 結論

對深部支護巷道在動力擾動下的動態破壞及支護體系響應進行了數值模擬，得到動載下巷道圍巖的破壞規律以及錨桿體系極限承載規律。主要結論如下：

1)深部巷道圍巖出現應力集中和塑性破壞，當沖擊應力波傳播至巷道附近，造成圍巖應力瞬間重新分布，沖擊應力波造成巷道壁積聚大量動能，易導致巷道壁片幫和巖塊彈射。

2)錨桿在強沖擊載荷下發生斷裂，錨桿失去支護能力。特定支護強度下僅能承受低于臨界強度的動力擾動，大于此強度的擾動會造成巷道的嚴重破壞。

3)巷幫圍巖距離動力擾動源距離近的位置破壞嚴重。采深與錨桿支護能力密切相關，深部巷道受沖擊擾動后圍巖變形幅度和錨桿失效個數都大幅增加。