結構化理念下的復習課設計

朱希萍 黃敏

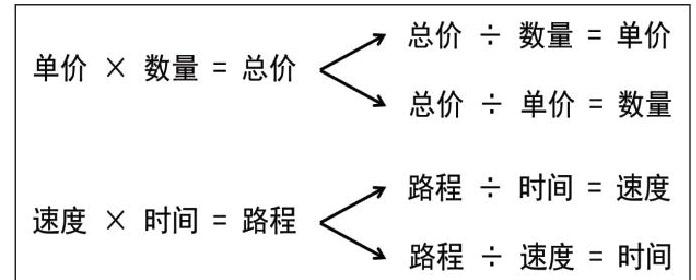
人教版教材四年級上冊“三位數乘兩位數”單元的例4、例5安排了兩種常見數量關系“單價×數量=總價”和“速度×時間=路程”，兩道例題都是以問題解決的形式揭示概念，對速度引入了復合單位，教材的編排可以將“單價×數量=總價”理解成“速度×時間=路程”的基礎。在這兩節課后需要安排一節復習課，對這兩個數量關系進行比較、溝通，讓學生把這兩個數量關系納入已有的認知。筆者以結構化理念為指導，對這節復習課做了如下設計。

【教學過程】

一、談話引入，回憶舊知

1.談話引入：我們已經學習了兩個非常重要的“量”——“單價”和“速度”，大家還記得嗎？

2.教師出示題目，引導學生討論交流。

（1）涌泉蜜橘單價80元，青蟹單價60元，哪個單價貴？

學生質疑后教師完善信息：80元/箱（一箱5千克），60元/只（3只約1千克）。得出：比較物體的單價要說明單位量。

（2）一種交通工具，速度是12千米，請你猜一猜它是什么。

生：是自行車，每小時12千米。

生：是飛機，每分鐘12千米。

師：速度是12千米的交通工具怎么一會是自行車，一會是飛機呢？

生：速度表示單位時間內行的路程，既要交代路程，也要交代時間。

教師完善信息：12千米/時（自行車的速度）;12千米/分——720千米/時（飛機的速度）。

3.深入探究：“單價”和“速度”有什么相同點和不同點？

（1）學生回憶后互相交流：單價是單位量的價格，速度是單位時間行駛的路程。

（2）適時引出共同點：它們都用復合單位表示一份的量。

小結：速度和單價的單位都要用復合單位，表示單位數量的商品價格或單位時間行駛的路程。

（思考：利用談話的方式進行知識回憶，主要針對學生比較難理解的單價與速度概念。學生會認為單價是錢數、速度是長度，缺少對這兩個重要概念所具有的“相對性”的理解。通過本環節的教學，學生既明白了單價的相對性，80元/箱是以箱為單位的單價，但是相對于一箱5千克，每千克16元，80元又成了總價，相對性得以體現;又明白了單價與速度分別表示單個量的價格與單位時間的路程，單價也可以用復合單位表示。）

二、“問題解決”中溝通聯系

1.教師出示表1、表2，請學生將表格填寫完整。

2. 組織反饋表1：仔細觀察表格內的數據變化規律，你有什么新的發現？

小結：數量不變，單價越高，總價越高。（聯系積的變化規律）

3. 組織反饋表2：比一比這三輛車誰最快。可能各是什么車？

比較甲車和乙車，路程相同可以比時間。比較乙車和丙車，時間相同可以比路程。

小結：速度用一個復合單位表示，因為它已涵蓋了時間和路程這兩個量的關系，比較時只要比一個量就可以了。單價、數量、總價三者之間也是同樣的道理。

4.繼續提問：如果丙車用這樣的速度也行駛360千米，需要多少時間？仔細觀察表格內數據的變化，能發現什么規律？

小結：路程不變，速度越快，時間越短。（再次聯系積的變化規律）

（思考：這一環節主要解決3個問題。這3個問題有的是數量一樣，單價在變;有的是速度一樣，時間在變，有的是求單價，有的是求速度，有的是求路程。學生解決問題后，感悟到單價不變，總價變化而引起數量的變化，與積的變化規律建立聯系。此外，通過比較三輛車的快慢，學生體會到用速度比較快慢的優越性，從而感悟速度反映了路程和時間兩個量之間的關系。）

三、自主編題，認知結構化

1.教師出示表3，請學生自由選擇題1或題2來編一編應用題。教師指導學生完成編題。

[1 根據80×4=320編一個求總價的應用題 根據320÷5=64編一個求單價的應用題 你能把前兩道題合并成一道應用題嗎？ 2 根據80×4=320編一個求路程的應用題 根據320÷5=64編一個求速度的應用題 你能把前兩道題合并成一道應用題嗎？ ]

2.分別反饋題1和題2，橫向分析比較。

（1）對前兩列中的題目，重點交流根據什么數量關系，怎樣用線段圖表示。

結合學生的回答，課件出示。

（2）對第三列，重點交流怎樣將兩個應用題合并成一個，什么變了，什么沒變。

（思考：本環節根據“80×4=320”編求總價、路程的題目，根據“320÷5=64”編求速度與單價的題目，既可以通過同組數量關系的各類應用題進行相互改編，幫助學生理解同組各類基本應用題幾個數量間的相互關系;也可以通過同一個式子解決不同問題情境，幫助學生形成應用意識。學生在編題中深刻感受到問題的結構，達到結構化教學的目的。）

3.縱向分析比較。

師：今天學習的“速度、時間、路程”與“單價、數量、總價”這兩類數量關系之間有什么關系？和我們以前學習的哪些知識比較相似？

生：和原來學的一份數、份數、總數的關系相似，單價是每件物品的價格，速度是單位時間行駛的距離，都可以表示每份數;數量與時間都表示有幾份（份數）;總價與路程表示總數。

生：都可以表示成一份數×份數=總數、總數÷一份數量=份數、總數÷份數=一份數。

生：都可以把它們看作因數與因數積的關系，因數×因數=積，積÷一個因數=另一個因數。

生：它們的變化規律和以前學習的積的變化規律一樣。

教師出示以下關系，完善結構。

（思考：此環節通過對數量關系的縱向比較，學生感受到求總價和求路程的相同點，求單價和求速度的相同點，都是求幾個幾是多少的問題。從乘法的意義出發進行理解，“速度、單價”只是每份數而已，“速度×時間=路程、單價×數量=總價”等數量關系只不過是“幾個幾連加的和”，體現了復習課的功能——通過比較聯系將離散的知識進行串聯溝通，歸位到知識的源頭，形成知識結構化。）

四、綜合練習，提升能力

教師出示練習：小王和12個同事一起從上海出發到臨海兩日游。請同學們根據以下信息，制訂出行計劃，并算出乘車和住宿的費用。

（1）旅游出行要考慮哪些事情？

（2）信息1：坐高鐵路程約540千米，時間3小時，票價190元; 坐汽車路程約360千米，平均速度約90千米/時，票價155元。 信息2：臨海某賓館房價雙人間為328元，單人間為218元。

在學生初步建立了數量關系知識結構以后，再把“數量關系”放回到學生熟悉的求乘車和住宿的總費用中進行運用。

（思考：做旅游預算，需要學生綜合運用本節課所復習的兩類常見數量關系，計算出不同乘車方式的時間和費用，以及不同住宿選擇安排的房間數和費用，這個過程既有單價、速度、時間等單一數量的比較和分析，又有節約費用、合理安排行程以及生活常識等方面的綜合考量，幫助學生在解決實際問題中積累活動經驗，提升學生發現問題、分析問題、解決問題的綜合能力。）

【教學反思】

這節課的設計有如下幾個特點。

一、難點處——結構化材料促進查漏補缺

復習課的一大功能是查漏補缺，查漏補缺用在學生的疑難處方能對癥下藥。學生對速度、單價的相對性的理解是難點，本節課通過結構化的材料：“涌泉蜜橘單價80元，青蟹單價60元，哪個單價貴？”讓學生在質疑討論中，感悟到單價、速度的相對性。在探究“一種交通工具，速度是12千米，請你猜一猜它是什么”的過程中，學生自然而然地理解了復合單位，學習難點得到了突破。

二、聯結處——結構化教學溝通聯系

溝通路程模型與總量模型。總量模型是指總量與幾個部分量之間的關系。總量模型適用于解決一類現實中的問題，比如可以解決“路程 = 速度 × 時間”“總價 = 單價 × 數量”的問題，也可以解決“總數 = 行數 × 列數”的問題，等等。“單價×數量=總價”和“速度×時間=路程”是人教版小學數學中安排的兩種常見數量關系。教學中教師要讓學生厘清兩者各自的特點，溝通它們之間的關系，還要讓學生弄明白它們與乘法的聯系。

三、伸展處——結構化思考提升素養

數學核心素養要求學生用數學的眼光觀察世界，用數學的思維思考世界，用數學的語言描述世界。本節課教學注重引導學生在理解“單價、數量、總價”三者關系的基礎上，推理速度、時間、路程的關系，并將這些關系設置在不同情境中加以運用，使學生意識到現實世界中的許多問題都可以用數學的方式來解決，培養學生的應用意識和模型思想。

（浙江省臨海市大洋小學? ?317000）