非線性塵埃等離子體孤立子波變分迭代解

徐建中, 汪維剛, 莫嘉琪

(1- 亳州學院電子與信息工程系，亳州 236800; 2- 合肥幼兒師范高等專科學校基礎部，合肥 230011;3- 安徽師范大學數學與統計學院，蕪湖 241003)

1 引言

近來在全球氣候變暖的情形下，加上人為等因素引起的大氣反常的事件，導致了大氣氣候的極端事件出現的幾率增加，譬如沙塵暴和霧霾等情形不斷地出現.大氣中塵埃的擴散現象對人們的生產和生活帶來了巨大的災害.這種氣候對空氣污染受到學術界的很大的關注.為改善大氣的質量和控制空氣中塵埃的污染，人們需要清楚大氣中塵埃顆粒物的分布狀況.但是空氣中塵埃顆粒物的產生有許多因素，這樣就影響了控制環境污染措施的制定.因此，我們需要對大氣塵埃顆粒物的了解并要在對氣象和塵埃污染數據監測和預報的基礎上開展更精細的計算，然后由計算的結果采取合適的措施.這樣有助于減少相應的環境污染和災害，促使大氣環境改善.

近年來，許多學者對大氣塵埃的研究十分重視[1,2]，Zhao 等對等離子體分離流的燃燒和控制作了研究[3]，Zhang 等對非恒溫的等離子體作的分析[4]，Wang 等研討了一類等離子體在屏障排放狀態下的影響[5]，馮依虎等求出了大氣量子等離子體孤立子波的漸近解[6]，很多科學工作者還研究了塵埃振動調制方面的穩定性[7]，Duan 等研究了一類塵埃等離子體的非線性波[8,9]，何廣軍等討論了塵埃顆粒大小及塵埃荷電量等離子體波的作用[10]等問題.

大氣塵埃等離子分布的規律先是通過一維KdV 方程描述的，許多學者作了很多的研究.是將橫向非線性波通過KP(Kadomtsev-Pctviashvili)方程來描述的.為了對大氣塵埃等離子體擴散有更深入的了解，一些科學工作者還對二維Einstein 凝聚系統做了討論[11,12].

關于非線性方程的問題，目前已經有較多改進的近似求解方法.作者等也用許多漸近的方法討論了一類非線性孤波、等離子體、塵埃和有關大氣物理問題[13-29].本文是用一個泛函分析的廣義變分迭代方法求得了一類廣義塵埃等離子體非線性孤立子波方程的漸近解析解.

二維低頻塵埃等離子體的無量綱流體動力學系統可表示為

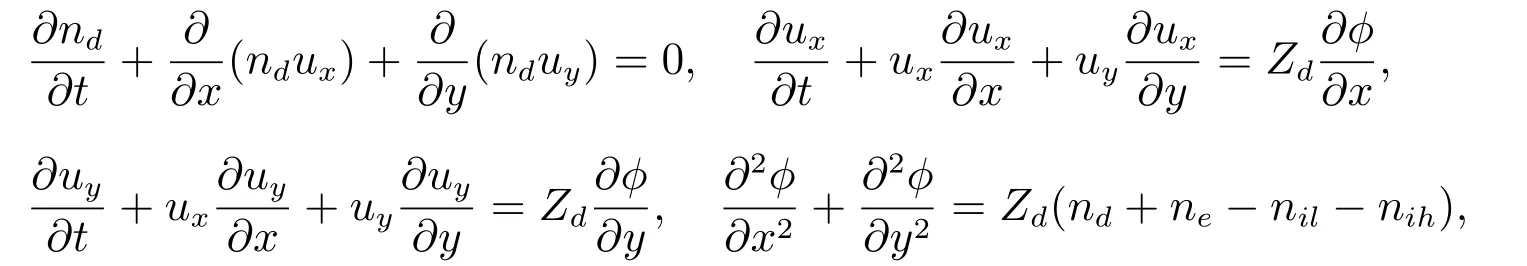
上式

nd=Ail0exp(?s?), nih=Aih0exp(?β1s?),

ne=Ae0exp(?β1s?), nil=Ail0exp(?s?),

而ux, uy為塵埃體在x 與y 的速度分量，md, nd為塵埃顆粒的質量和密度，Qd= eZd是塵埃顆粒上的荷電量，

而TeTil和Tih是電子、低溫離子和高溫離子的溫度.

2 典型塵埃等離子體方程孤立子波解

設電子和離子的流速小于熱運動速度，作一些變量變換，可得廣義KP 方程

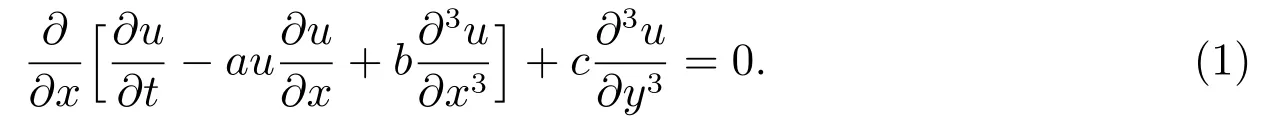
作如下行波變換

這里ki(i=1,2,3)為常數.由式(2)得方程(1)以自變量s 的常微分方程

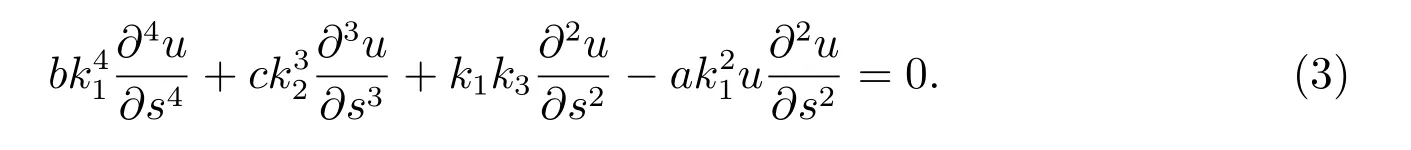
由于方程(3)是具有代數型項的非線性常微分方程，因此，現采用雙曲函數待定系數的方法來求孤立子波解[1].設微分方程(3)具有如下的形式的待定解

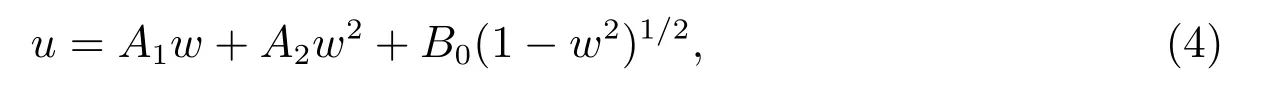
這里A1, A2, B0為待定常數，而w 滿足微分方程

易知，方程(5)有解

由(4)和(5)式有

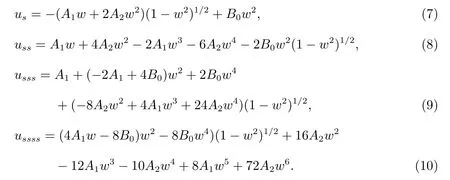
將式(4),(7)–(10)代入常微分方程(3)，可得

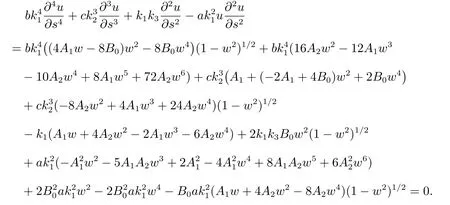
合并上式中的同類次冪的項，且設各次冪項的系數為零，得到

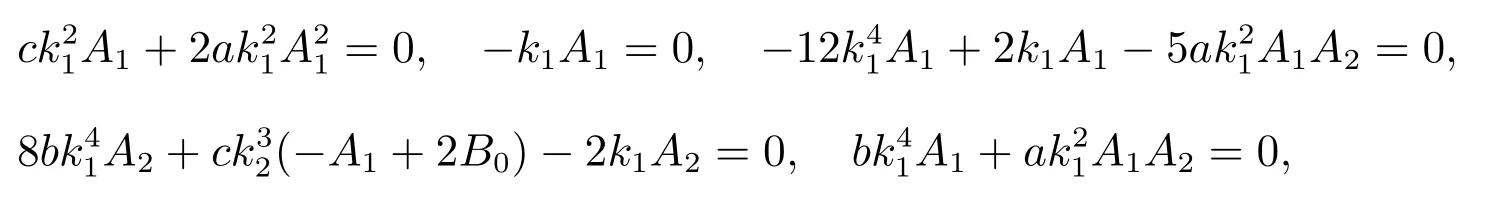
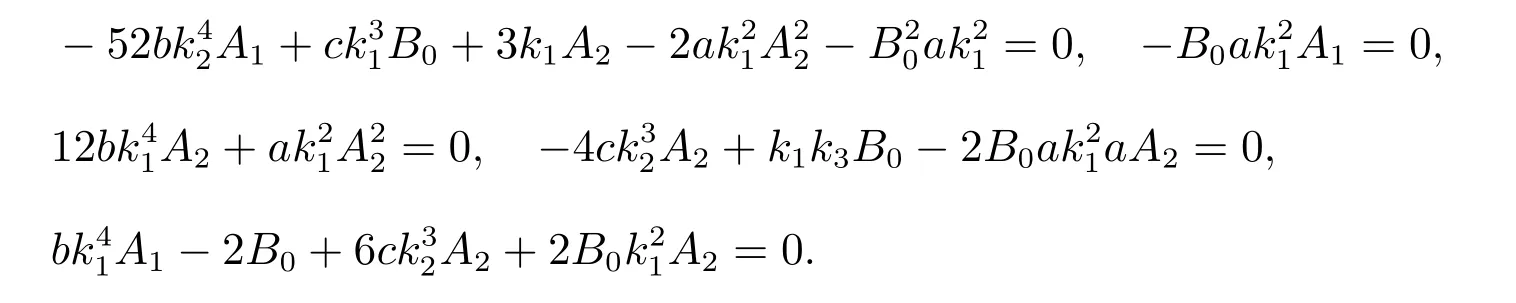
由上面諸式得到

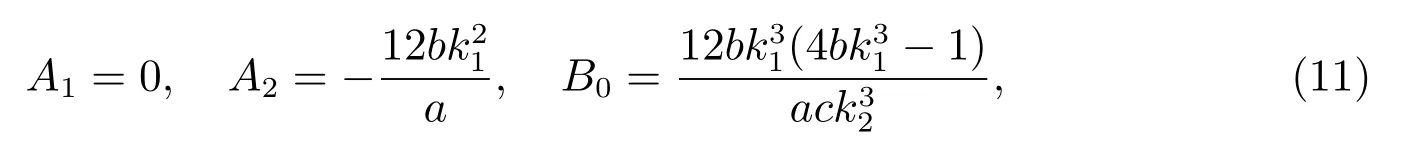
這里k1, k2滿足

將式(11)和式(6)代入式(4)，可得廣義KP 方程(1)如下孤立子波解

今取無量剛參數a = b = c = k2= 1, k1= 1/4，則式(14)表示的孤立子波的曲線圖形，如圖1 所示.

再選取無量剛參數a = b = c = k1= k2= 1，則式(14)的孤立子波曲線的圖形，如圖2 所示.

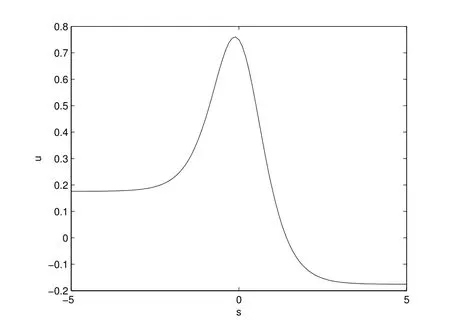
圖1: 式(14)的孤立子波曲線 (a=b=c=k2 =1, k1 =1/4)

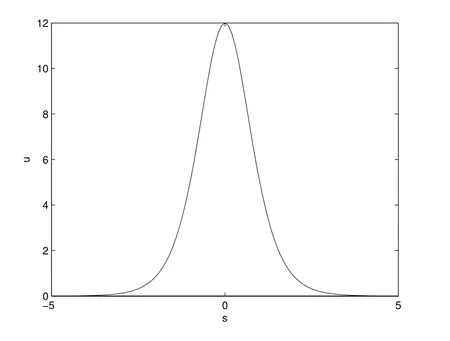
圖2: 式(14)的孤立子波曲線(a=b=c=k1 =k2 =1)

由行波變換(2)，便得到廣義KP 方程(1)的孤立子行波解

其中k1, k2由式(12),(13)決定.

3 廣義塵埃等離子體方程孤立子波解

現討論二維塵埃等離子體低頻振動廣義非線性擾動KP 方程

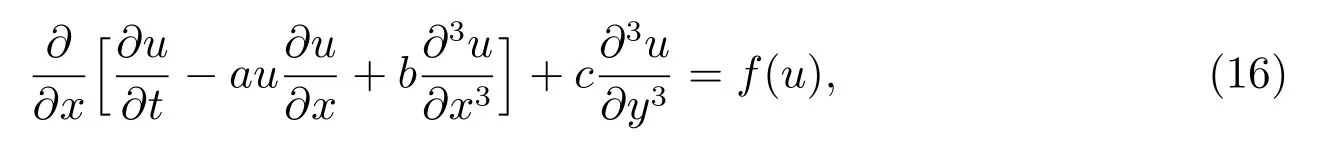
這里a, b, c 是常數；f(u)是低頻塵埃聲波擾動項，此擾動項為粒子之間的碰撞、電子附著等原因引起的，不妨設它為充分光滑的有界函數.

在變換(2)下，廣義非線性擾動KP 方程(16)轉化為常微分方程

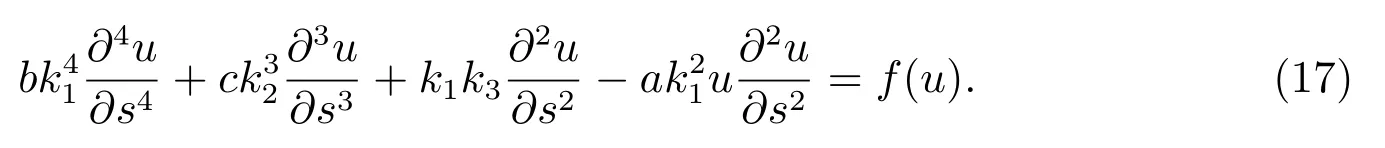
現用廣義變分迭代的方法[30]求塵埃等離子體低頻振動廣義擾動KP 方程(17)式近似孤立子波解析解.

構造一個泛函

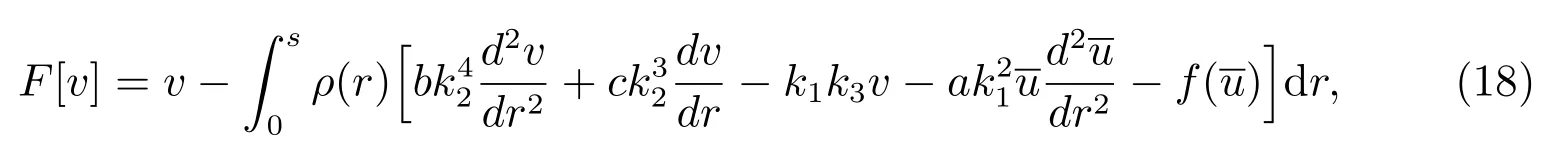
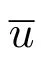
計算泛函(18)的變分

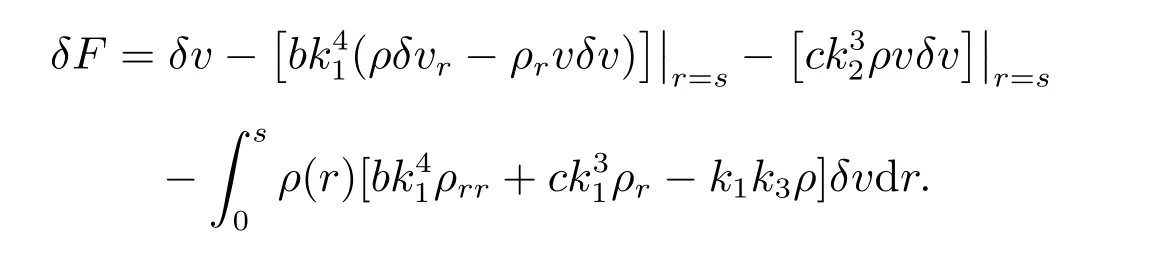
根據變分的極值理論，取δF =0，得到

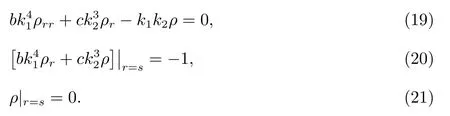
上述初值問題(19)–(21)的解ρ(r)為

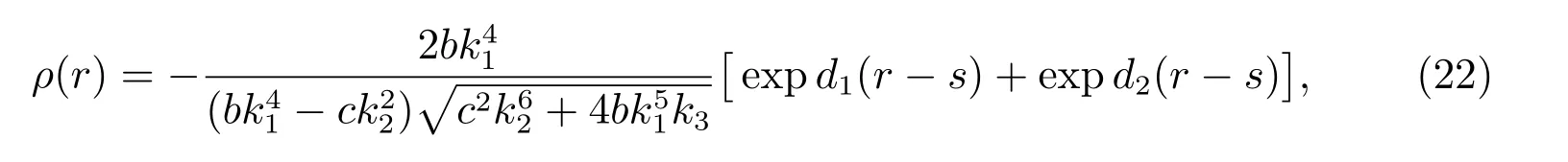
這里

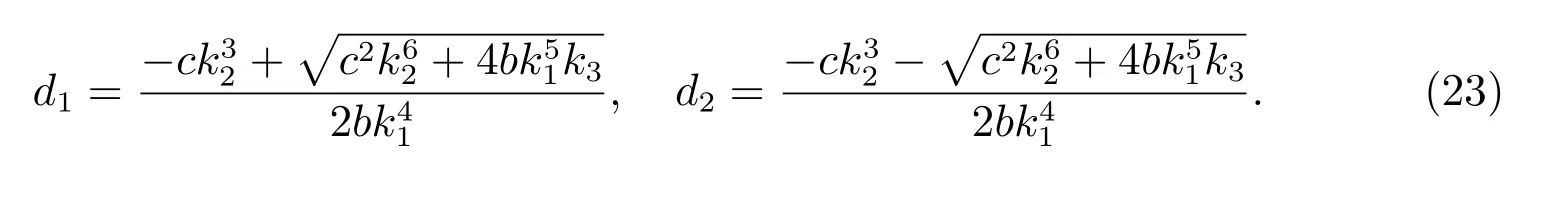
因此，由式(18),(22)，構造如下迭代式

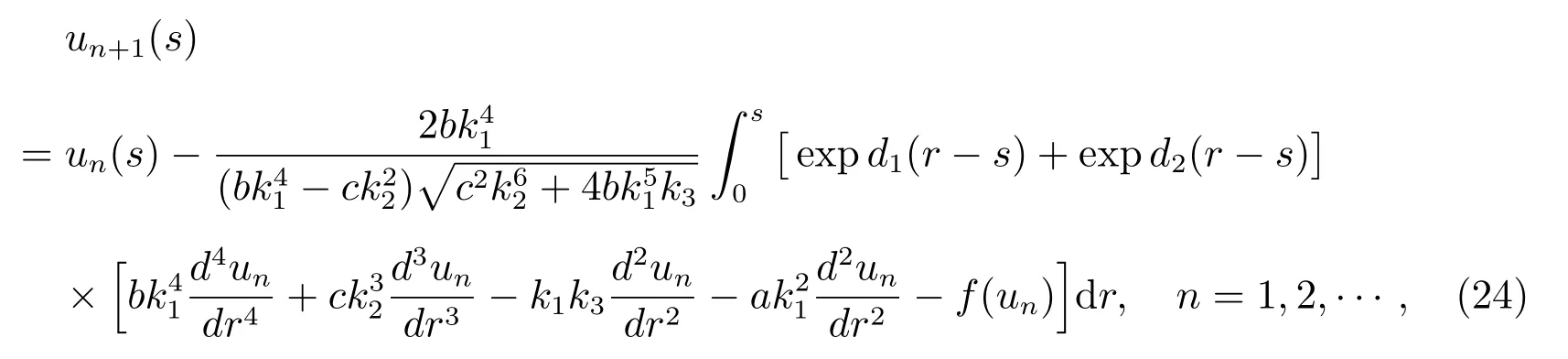
這里ki(i=1,2,3), di=1,2 由式(12),(13)和(23)決定，而u0是初始近似函數.由變分迭代式(24)，當選取初始近似以后，就可得依次得到un(s)(n=1,2,···).

再由變換式(2)，可得廣義擾動KP 方程(16)的第n 近似孤立子波行波解un(k1x+k2y ?t)(n=0,1,2,···)：

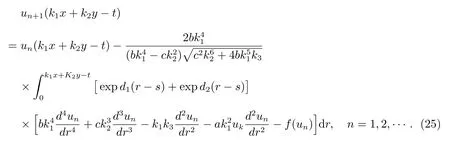
因此，我們得到了函數序列un(t,x,y)(n=0,1,2,···)，由變分理論有如下引理[30].

引理1un(t,x,y)在(t,x,y) ∈[0,T]×[0,M]2上為一致收斂的序列，其中T, M 為任意的正常數.

由上述引理，函數序列{un(t,x,y)}在(t,x,y)∈[0,T]×[0,M]上存在一個極限函數

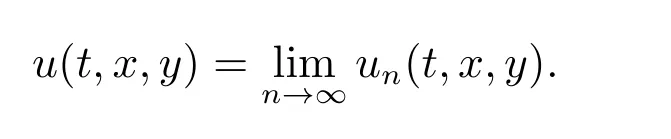
因此有如下定理.

定理1二維塵埃等離子體低頻振動廣義非線性擾動KP 方程(16)，當f(u)為低頻塵埃聲波的擾動項是關于其變量為充分光滑的有界函數時，由(26)決定的極限函數u(t,x,y)是塵埃等離子體低頻振動非線性廣義擾動KP 方程(16)的精確解.

4 例子

現來考慮一個簡單的無量剛塵埃等離子體低頻振動非線性廣義擾動KP 方程例子.設a=b=c=1，而擾動項為f(u)=exp[?u2].

由式(16)，塵埃等離子體非線性廣義擾動KP 程為

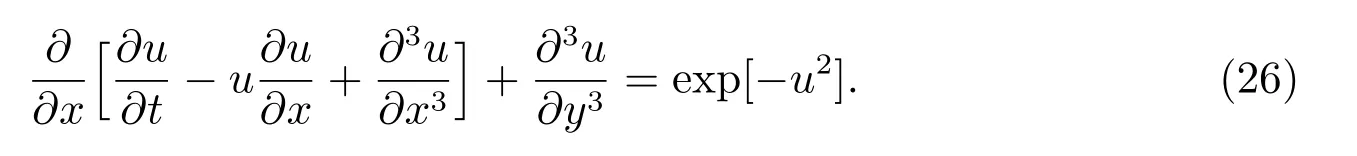
作行波變換s=k1x+k2y ?t，由式(17)，廣義擾動KP 方程(26)為

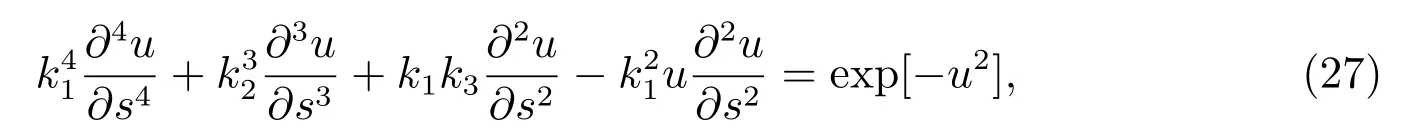
這里ki(i=1,2,3)由式(12),(13)決定.

用前述變分迭代關系式(24).選取初始近似u0(s)為方程(1)的孤立子波解.即由(14)式得

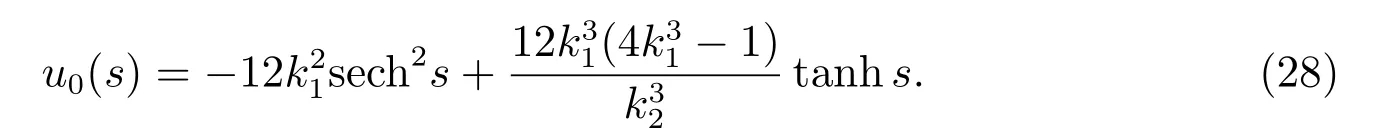
由式(28)和(24)，可得非線性廣義擾動KP 方程(27)解u(s)的一次近似

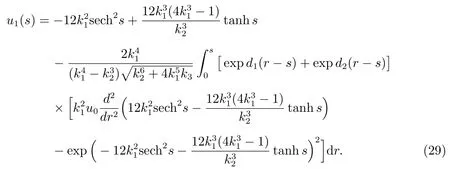
再由(28),(24)式，可求出擾動非線性廣義擾動KP 方程(26)解u(s)的二次近似

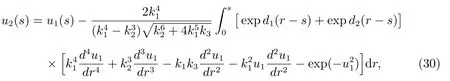
這里ki, di由式(12),(13),(23)決定，u1由式(29)表示.

繼續利用迭代式(24)，可得到塵埃等離子體低頻振動非線性廣義擾動KP 方程(26)解u(s)的更高的n(n=3,4,···)次近似un(s).

再繼續由行波變換(2)，可得到廣義擾動KP 方程(16)的第n 近似的孤立子波行波解un(t,x,y)=un(k1x+k2y ?t)(n=0,1,2,···).

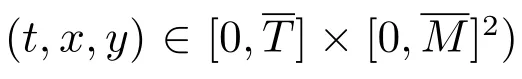
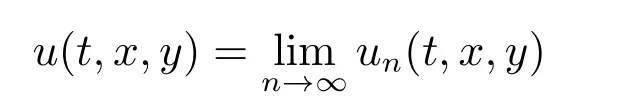
就是塵埃等離子體低頻振動非線性廣義KP 方程(27)的精確解.

5 結語

變分迭代理論和方法是通過求泛函的極值來得到對應的Lagrange 乘子.選擇適當的初始近似以后，能得到較高精度的近似解.由本文求得的是廣義擾動KP 方程塵埃等離子體的低頻振動孤立子波的近似解析解.它還可進行解析運算求出相關物理性態，如通過得到的孤立子波波峰值，并采取適當的措施避免“共振”現象而出現電荷超高密度的聚集而導致放電擊穿現象等等.關于這方面的進一步的情形，本文不再繼續研究.