四階Cahn-Hilliard 方程的間斷有限元方法

鄒樂強(qiáng), 劉麗杰, 韋雷雷

(1- 河南工業(yè)和信息化職業(yè)學(xué)院，焦作 454000; 2- 河南工業(yè)大學(xué)理學(xué)院，鄭州 450001)

1 引言

在本文中，我們考慮如下的四階Cahn-Hilliard 方程

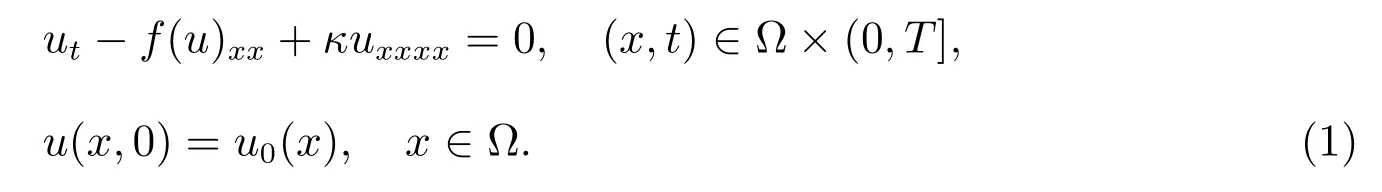
考慮周期邊值條件，其中κ ≥0, ? ∈R，f(u)是光滑函數(shù).注意到這里周期邊界條件的假設(shè)僅僅是為了問題討論的簡單，并不是本質(zhì)的，間斷有限元方法能夠直接推廣到非周期邊值問題.

四階的Cahn-Hilliard 方程首先是由Cahn 和Hilliard[1]于1958 年在研究二元合金的分離現(xiàn)象時(shí)提出的，隨著現(xiàn)代科學(xué)技術(shù)的不斷發(fā)展，該方程的應(yīng)用也越來越廣泛，如多相流中的界面動力學(xué).一些學(xué)者對四階Cahn-Hilliard 方程的數(shù)值方法有著濃厚的興趣，如有限元方法[2–12]，間斷有限元方法[13–16]，多重網(wǎng)格法[17–19]以及有限差分法[20–22].本文的主要工作是對四階Cahn-Hilliard 方程構(gòu)造一種間斷有限元格式，并進(jìn)行了理論分析和數(shù)值測試.我們所設(shè)計(jì)的間斷有限元方法與文獻(xiàn)[13–16]中所使用的是不同的.在文獻(xiàn)[13]中作者所使用的數(shù)值方法，是在時(shí)間上運(yùn)用間斷有限元方法進(jìn)行離散，而本文所考慮的是在空間上進(jìn)行間斷有限元方法離散.文獻(xiàn)[14]中所研究的是局部間斷有限元方法，與我們所構(gòu)造的方法是不同的.在文獻(xiàn)[15]中作者用標(biāo)準(zhǔn)的C0有限元形函數(shù).在文獻(xiàn)[16]中所使用的是一種內(nèi)罰間斷有限元方法.

間斷有限元方法的基函數(shù)是完全間斷的分片多項(xiàng)式，將分片多項(xiàng)式空間作為近似解和試驗(yàn)函數(shù)空間，目前該方法已在許多領(lǐng)域中得到應(yīng)用，如氣象學(xué)、天氣預(yù)報(bào)、渦輪機(jī)、湍流、淺水波模型、海洋學(xué)、氣動力學(xué)、粒子流、石油勘探、磁動力學(xué)、電磁學(xué)等.最初間斷有限元主要用來解決雙曲問題，后被推廣到其他問題中，得到了很好的結(jié)果.間斷有限元方法具有一致高精度的特點(diǎn)，而且通過選取單元插值多項(xiàng)式的次數(shù)，就可以提高數(shù)值精度，在實(shí)現(xiàn)p 自適應(yīng)方面，具有很大的優(yōu)勢[23].同時(shí)由于解的間斷性假設(shè)，對網(wǎng)格正則性的要求并不是很高，所以該方法不需要考慮傳統(tǒng)有限元方法中連續(xù)性的限制條件，就能夠?qū)W(wǎng)格進(jìn)行處理，很容易實(shí)現(xiàn)h 自適應(yīng).間斷有限元方法具有非常好的局部緊致性而且易于實(shí)現(xiàn)并行計(jì)算.

2 符號和理論結(jié)果

這部分將介紹一些文中要用到的符號和一些理論結(jié)果.

為方便起見考慮一維情形，?=[a,b]，對網(wǎng)格進(jìn)行剖分

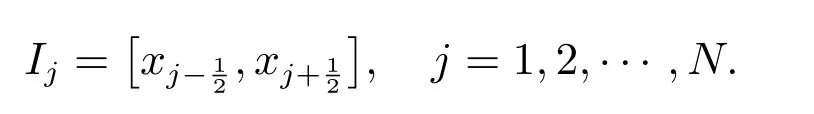
區(qū)間的中點(diǎn)為

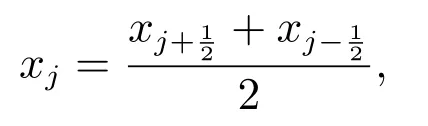
區(qū)間長度為

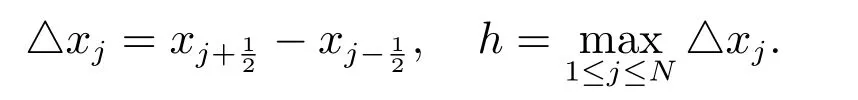
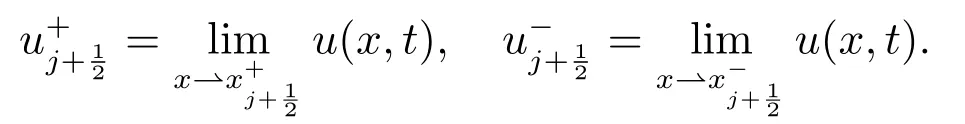
定義如下的有限元空間

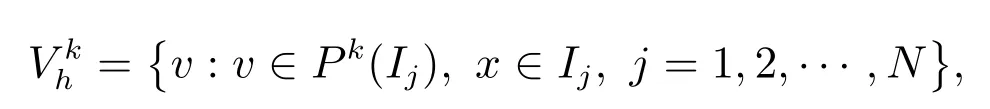
其中Pk(Ij)表示Ij上次數(shù)不超過k 的多項(xiàng)式集合.

對任意的vh∈Vkh，存在與vh和h 無關(guān)的λi(i=1,2,3)，使得

其中τh表示單元端點(diǎn)的集合，對以上性質(zhì)的詳細(xì)證明可參考文獻(xiàn)[24].

如果k ≥4，我們可以選取空間Vkh上的投影Ph，使得對任意的u, Phu 滿足

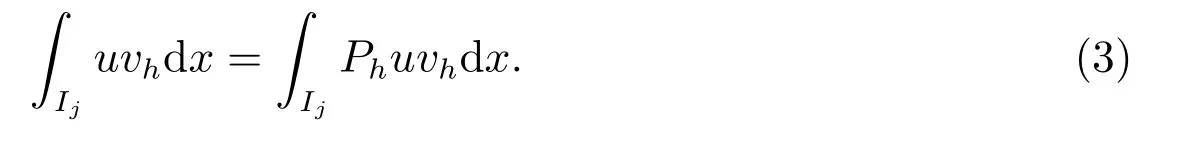
對任意的vh∈Vk?4h，且

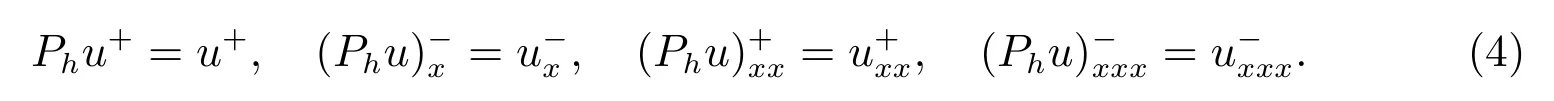
令η =u ?Phu 表示投影誤差.由逼近論[25–27]，可以得到

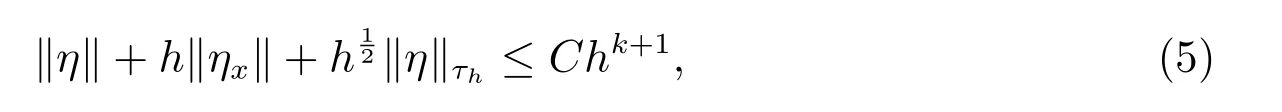
其中C 與h 無關(guān)，∥η∥τh表示在τh上的L2范數(shù)

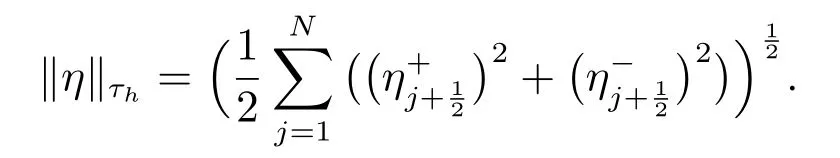
3 間斷有限元方法

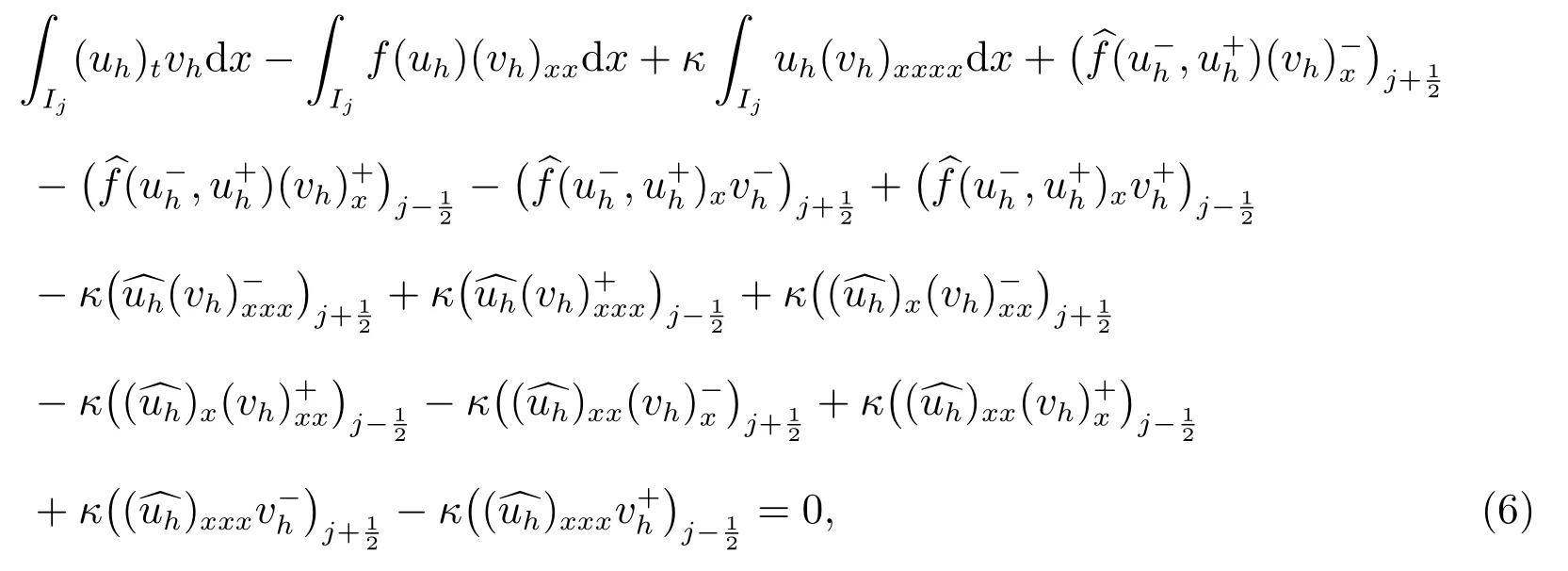
對任意的vh∈Vkh, j =1,2,··· ,N.

這里帶“∧”的項(xiàng)是數(shù)值流通量，可以選取

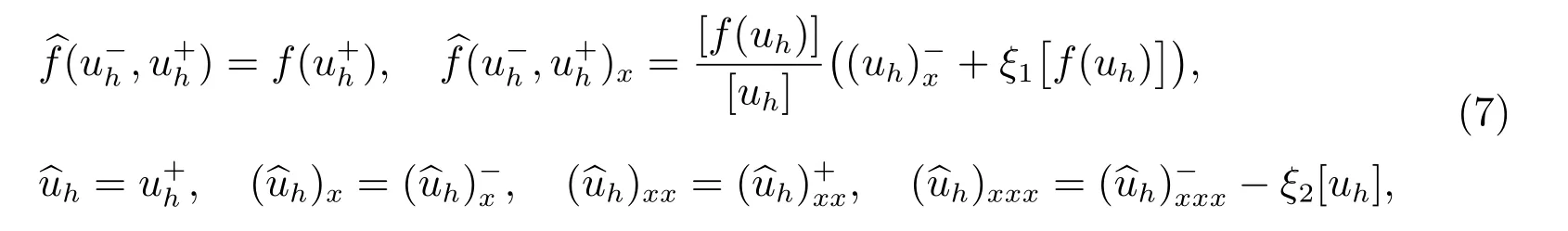
這里ξ1, ξ2是很小的正數(shù)，階分別為O(h?1), O(h?3).與傳統(tǒng)的局部間斷有限元方法相比，我們可以看到在流通量中出現(xiàn)了ξ1[f(uh)]和ξ2[uh]等懲罰項(xiàng).為了格式的穩(wěn)定性，這些懲罰項(xiàng)是必須的.

3.1 穩(wěn)定性

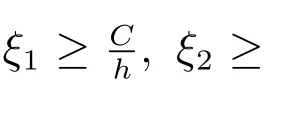
∥uh(t)∥≤∥uh(0)∥.

證明 在格式(6)中，我們?nèi)h=uh，關(guān)于j 相加，可得

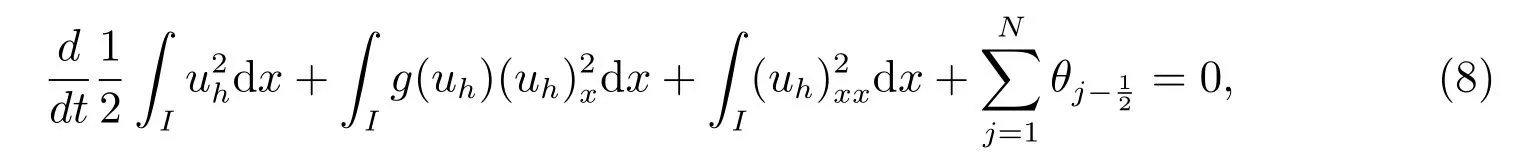
其中

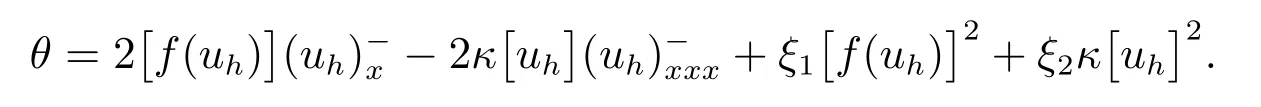
由(8)，可以得到

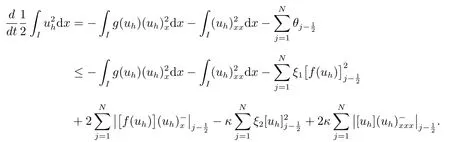
運(yùn)用性質(zhì)(2)，可知存在常數(shù)C，使得

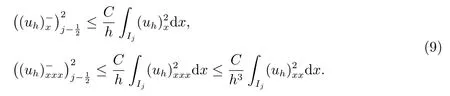
由Young 不等式，可以得到

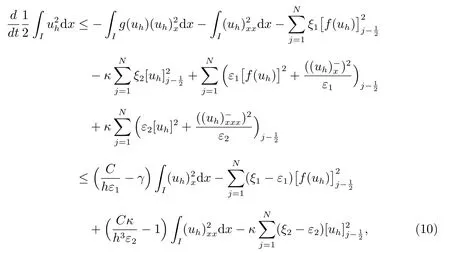
其中ε1, ε2>0.

令

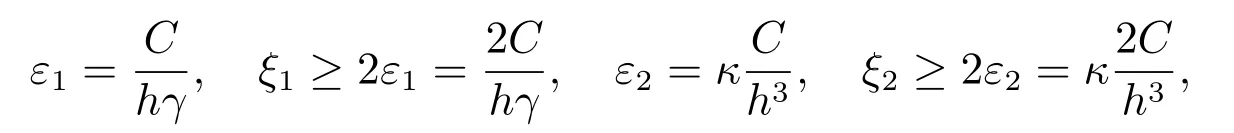
上式(10)可化為

對上式兩端從0 到t 關(guān)于時(shí)間做積分，可得

∥uh(t)∥≤∥uh(0)∥.

3.2 誤差估計(jì)

我們考慮線性情況f(u)=u 時(shí)格式(6)的誤差估計(jì).

定理2光滑函數(shù)u 是問題(1)的精確解，uh是格式(6)的數(shù)值解，數(shù)值流通量為(7)，在周期邊界條件下，當(dāng)k ≥3，我們有下面的誤差估計(jì)結(jié)果

∥uh(t)?u(t)∥≤Chk?1.

常數(shù)C 依賴于k, t, ∥u∥，與h 無關(guān).

證明 令e=u ?uh表示數(shù)值解與精確解之間的誤差，我們可以得到如下的單元誤差估計(jì)∫

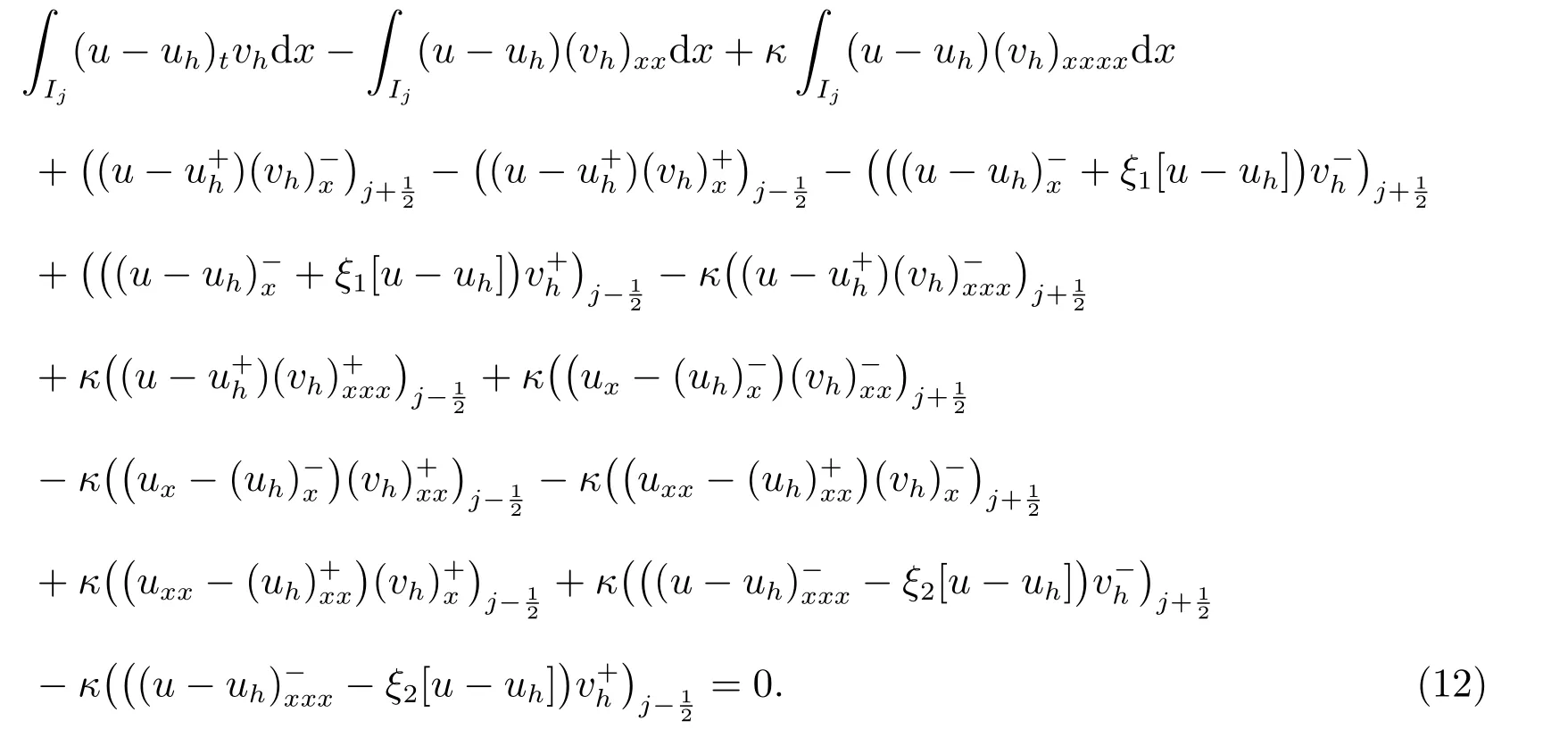
為簡單起見，定義符號

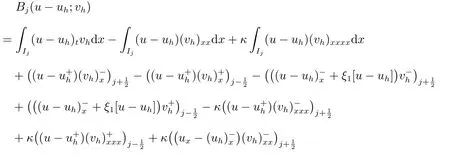
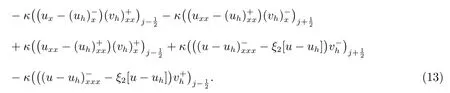
令wh=Phu ?uh, we=Phu ?u.取vh=wh，可得

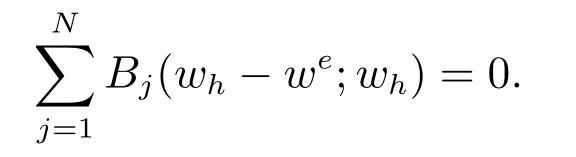
當(dāng)k ≥4，上面式子的左邊為

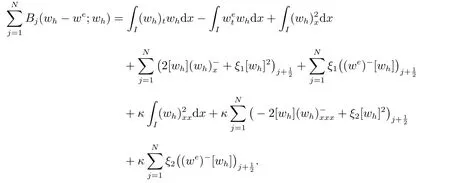
由投影性質(zhì)(3)–(5)和穩(wěn)定性結(jié)果，可得

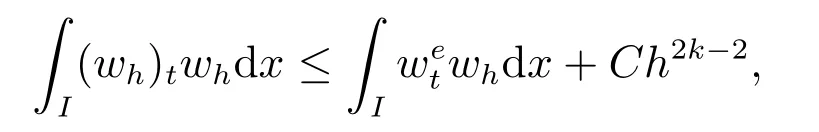
即

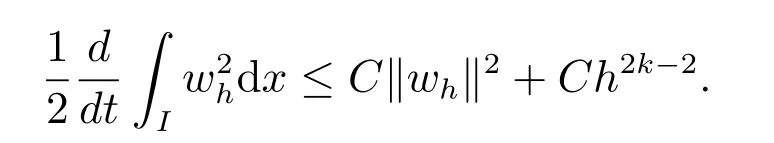
當(dāng)k ≥4 時(shí)，定理2 得證.

當(dāng)k =3 時(shí)的證明和k ≥4 的方法類似.所不同的是我們采用另外一種投影Qh：對函數(shù)u,

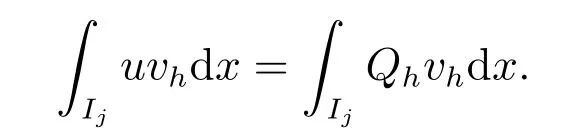
對任意的vh∈V0h，而且

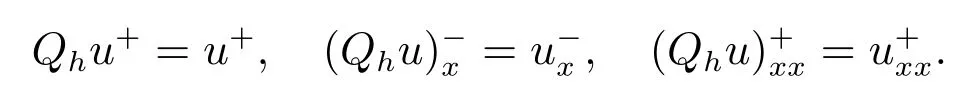
由逼近論[24]，可得

同樣定義wh=Qhu ?uh, we=Qhu ?u，可得

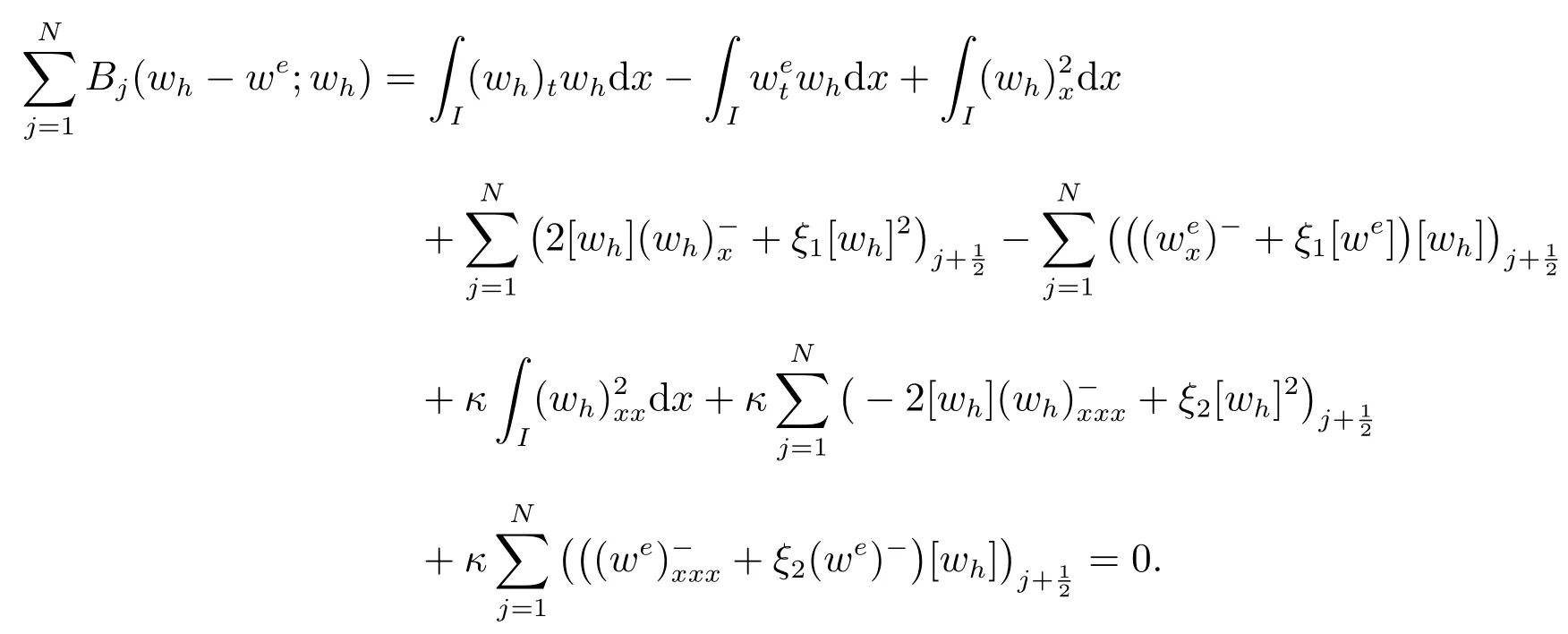
根據(jù)穩(wěn)定性結(jié)果，我們可以得到

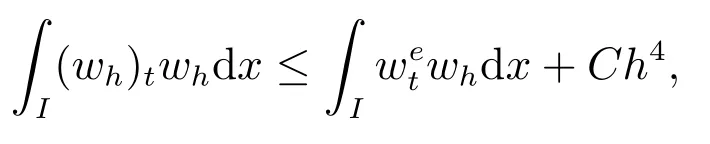
可知

當(dāng)k =3 時(shí)，定理2 得證.

4 數(shù)值算例

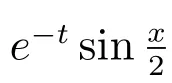
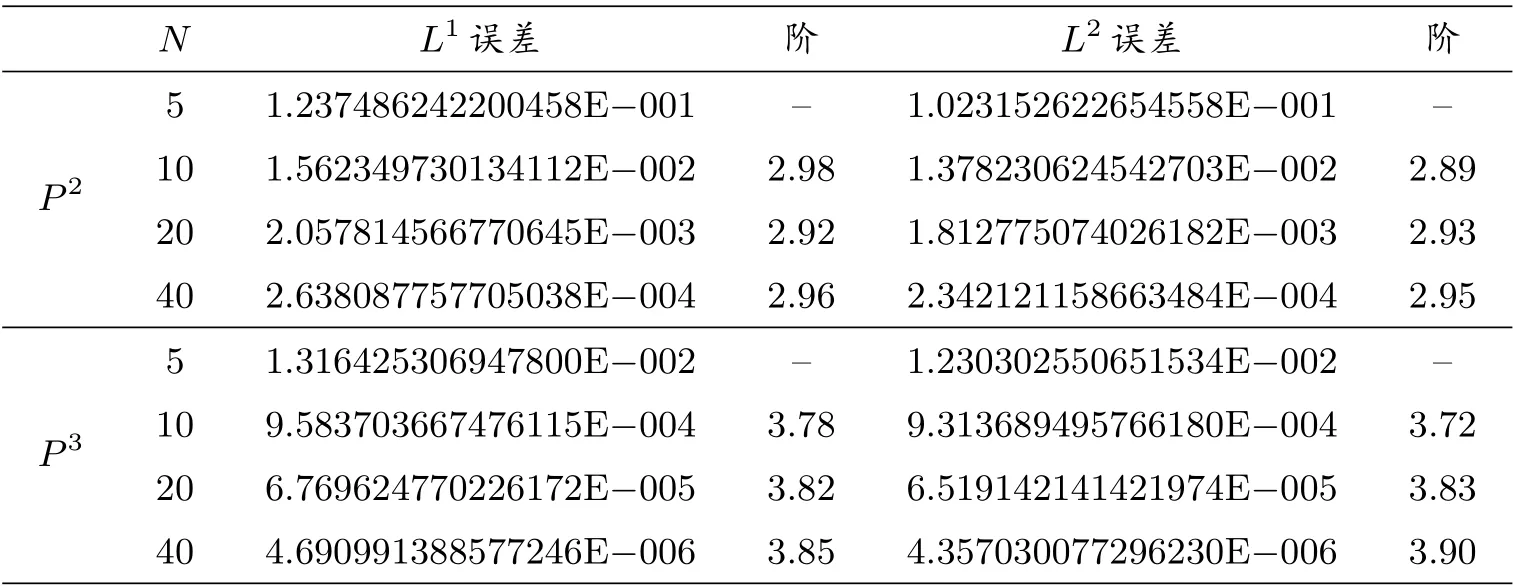
表1: 間斷有限元格式(6)的精度測試結(jié)果，T =0.5

5 總結(jié)

在本文中我們研究了四階Cahn-Hilliard 的間斷有限元方法，證明了方法的穩(wěn)定性和收斂性.該方法不同于傳統(tǒng)的局部間斷有限元方法，不需要引進(jìn)額外的輔助變量或?qū)⒎匠虒憺橐浑A的方程組，能夠減少計(jì)算量和存儲量.下一步，我們計(jì)劃將該方法推廣到其他含有高階導(dǎo)數(shù)的問題，并考慮與交替方向法結(jié)合來數(shù)值求解高維問題.