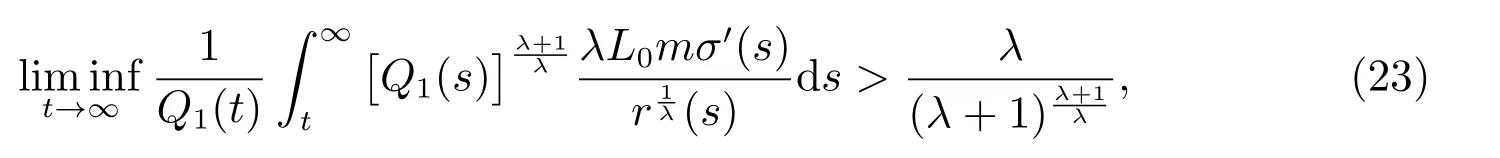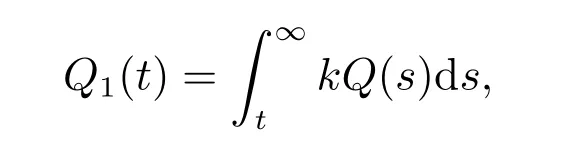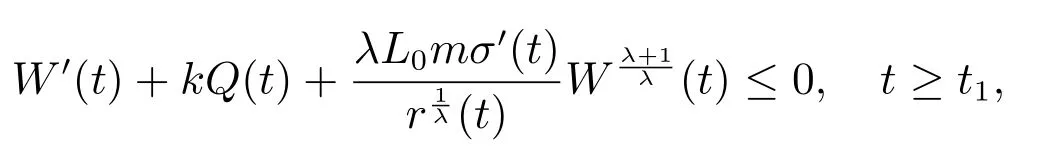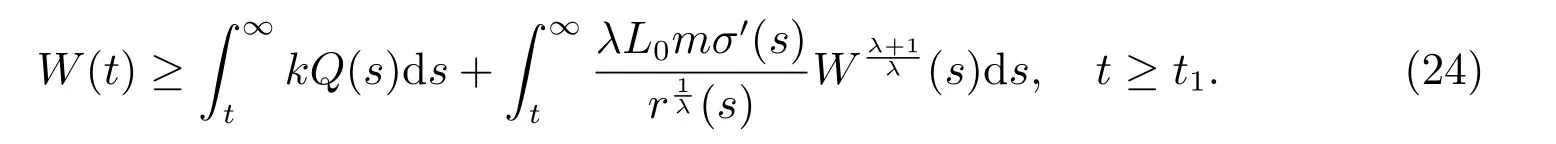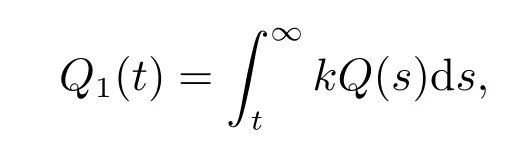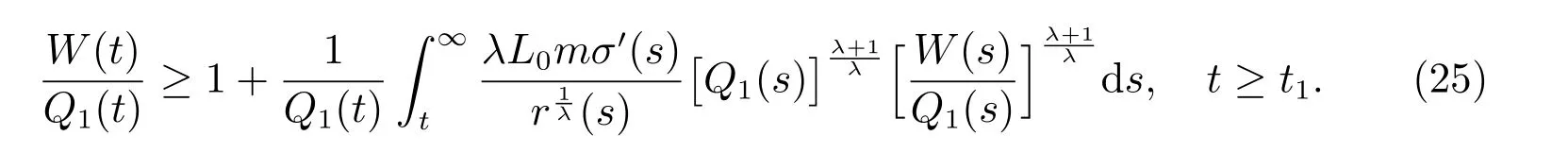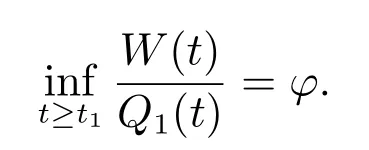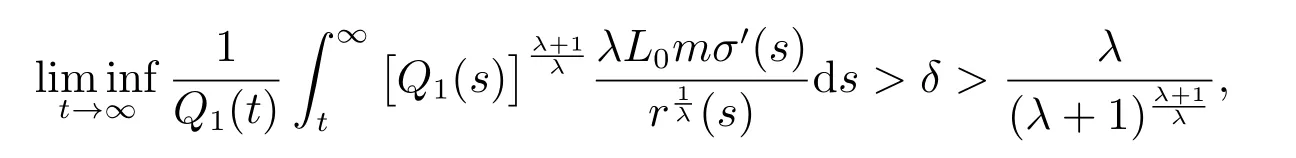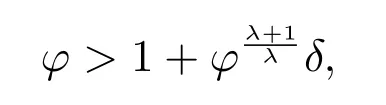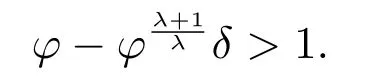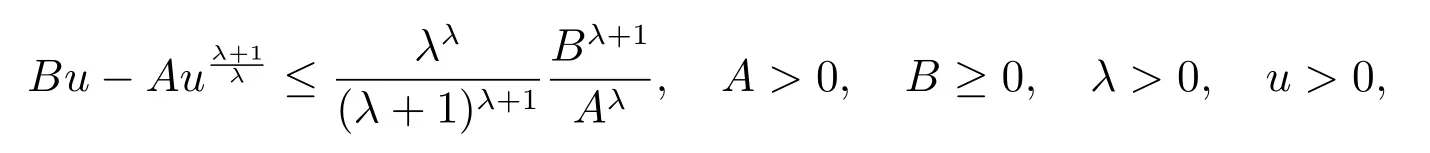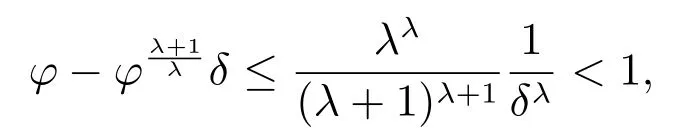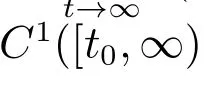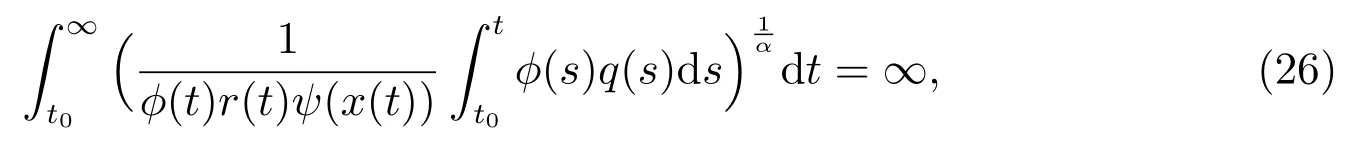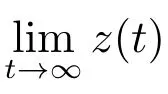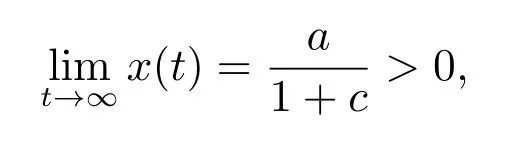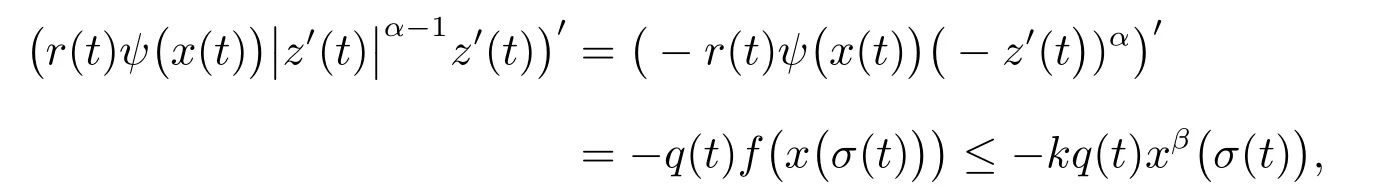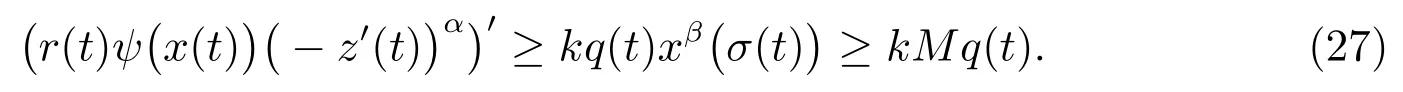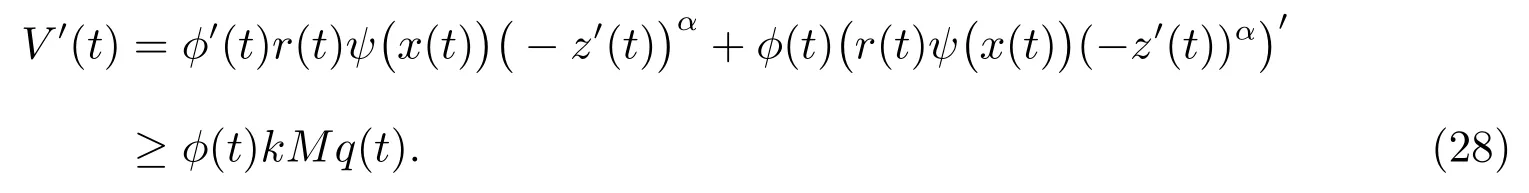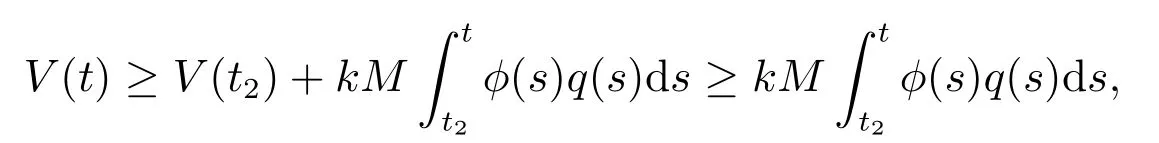二階擬線性中立型時滯微分方程的振動性
李文娟, 李書海, 湯 獲
(1- 赤峰學院數學與統計學院,赤峰 024000; 2- 赤峰學院應用數學研究所,赤峰 024000)
1 引言
本文考慮二階擬線性中立型微分方程
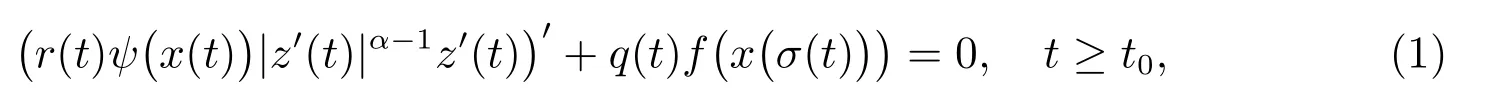
其中z(t)=x(t)+p(t)x(τ(t)), r ∈C1([t0,∞),R), p 和q ∈C([t0,∞),R), α 和β 是兩個常數.本文總假設下列條件成立:
(H1): α>0, β >0;
(H2): 0 ≤p(t)≤1, q(t)≥0;
(H3):
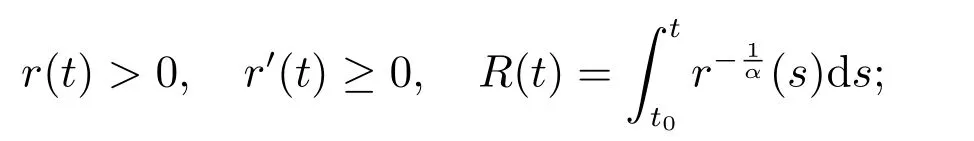
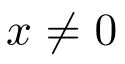
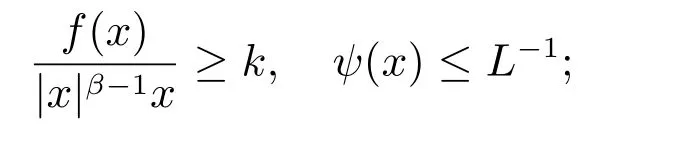
(H5):
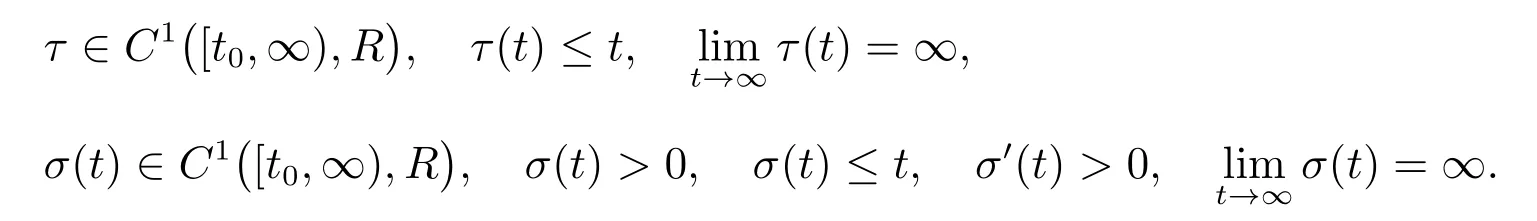
設Tx=min{τ(T),σ(T)}, T ≥t0.若x ∈C1([Tx,∞),R)適合
r(t)ψ(x(t))|z′(t)|α?1z′(t)∈C1([Tx,∞),R),
且在[Tx,∞)上滿足方程(1),則稱x 為方程(1)的一個解.本文僅考慮方程(1)的非平凡解,即對一切t ≥Tx,方程(1)在[Tx,∞)上的解x 滿足sup{|x(t)| : t ≥T} > 0 情形.如果方程(1)的解有任意大的零點,則稱其解為振動的,否則,稱它為非振動的.若方程(1)的一切解均為振動的,則稱方程(1)為振動的.
近年來,二階擬線性中立型微分方程在自然科學和工程技術中的應用日益廣泛,許多學者對其振動性的研究有著濃厚的興趣.2010 年,文獻[1]考慮了擬線性中立型微分方程
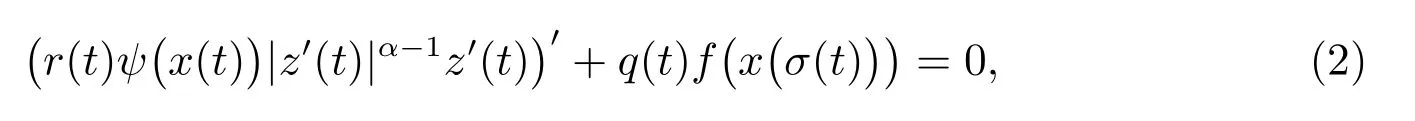
其中
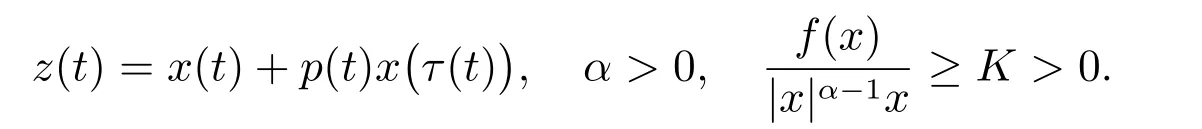
2011 年,文獻[2]考慮了Emden-Fowler 中立型方程
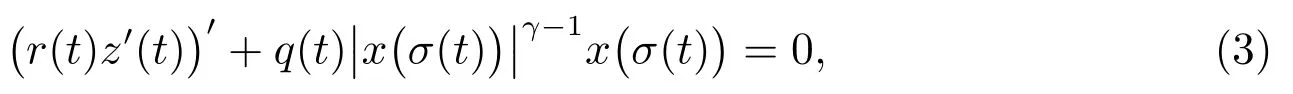
其中
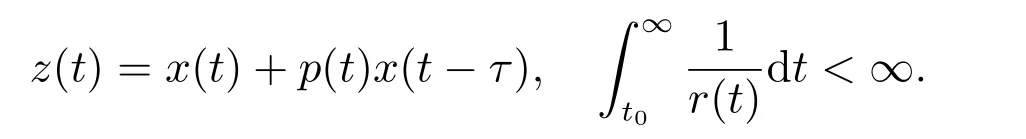
2012 年,文獻[3]考慮了擬線性中立型方程
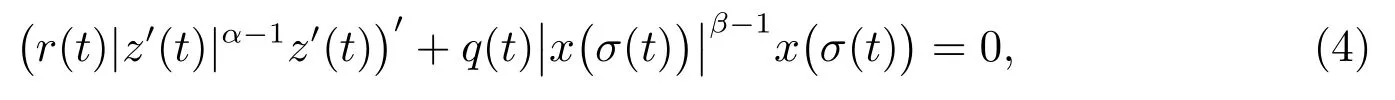
其中
z(t)=x(t)+p(t)x(τ(t)), α ≥β >0.
2015 年,文獻[4]進一步研究了方程(4),分別給出了當α ≥β >0 和β ≥α>0 時,方程(4)新的振動準則,改進了文獻[3]的結果.
最近,Agarwal 等人在文獻[5]中考慮了半線性中立型微分方程
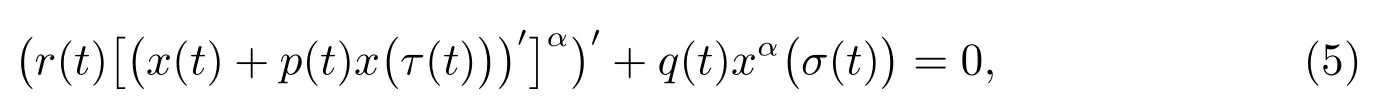
討論了非正則條件,即

下方程(5)新的振動準則,改進了文獻[1]的結果.我們注意到,雖然Emden-Fowler 中立型方程(3)不含在半線性方程(5)中,但它在粒子物理學中有非常重要應用,且上述方程(2)–(5)均為本文所考慮方程(1)的某些特例.在上述工作的基礎上,本文通過導出新的Riccati 不等式,利用積分平均方法給出方程(1)新的振動準則,所得結果改進了文獻中已有結果.
下面,我們分別討論在非正則條件(6)和正則條件

下方程(1)的解的振動性.
2 主要結果及證明
定理1設條件(H1)–(H5)和(7)成立,且存在函數ρ ∈C1([t0,∞),R+)和0 < m ≤1,使得
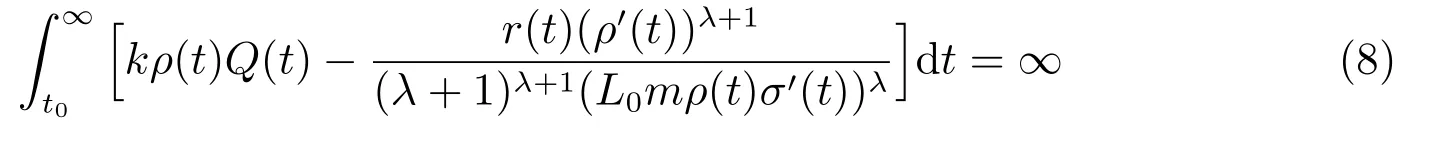
成立,其中

則方程(1)振動.
證明 設x 為方程(1)的一個非振動解.不失一般性,不妨設x 為最終正解,則存在t1≥t0,使得當t ≥t1時,有x(t) > 0, x(τ(t)) > 0, x(σ(t)) > 0.如果x 為最終負解,可用同樣的方法來討論.由方程(1)和假設條件可得到
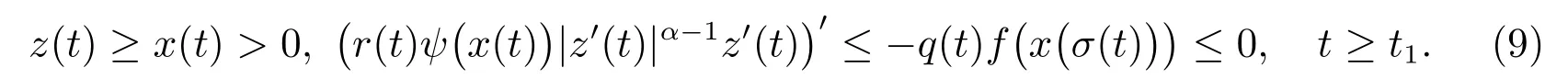
因此,r(t)ψ(x(t))|z′(t)|α?1z′(t)是非增函數且z′(t)最終保號,于是z′(t)僅有兩種可能.可斷言z′(t)>0,否則假設z′(t)<0, t ≥t2≥t1.
利用函數r(t)ψ(x(t))|z′(t)|α?1z′(t)是非增函數可知,存在正常數h,使得
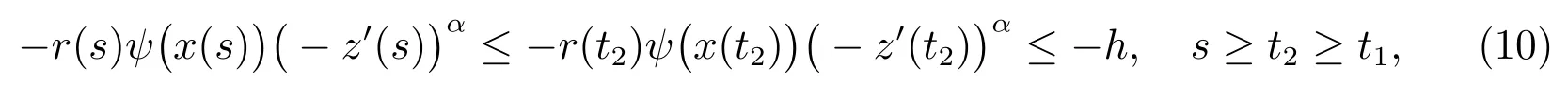
即
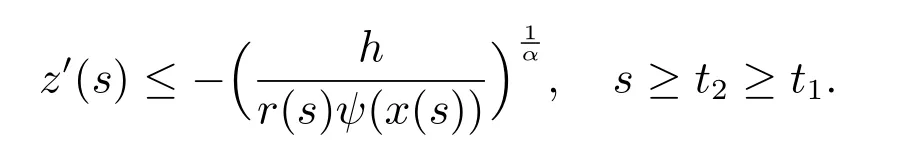
對上式從t2到t 積分,得
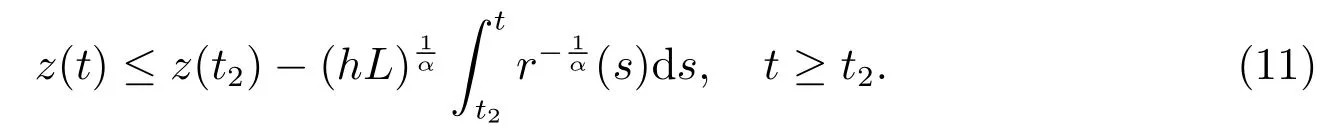
另一方面,由于r(t)ψ(x(t))|z′(t)|α?1z′(t)是非增函數且z′(t)>0,故有
r(t)ψ(x(t))(z′(t))α≤r(σ(t))ψ(x(σ(t)))(z′(σ(t)))α, t ≥t1,
即
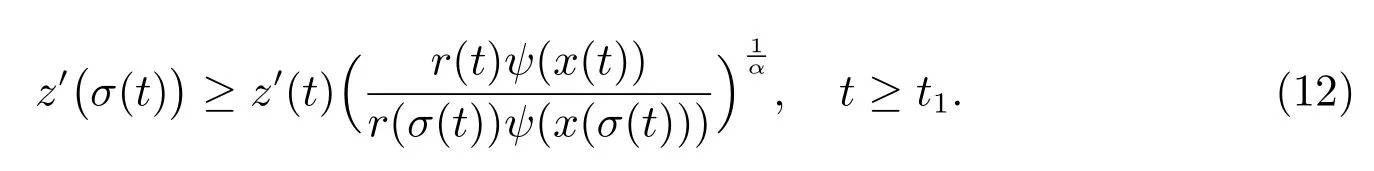
又由τ(t)≤t 和z′(t)>0,可得

再由條件(H4)、方程(1)和(13)式,得
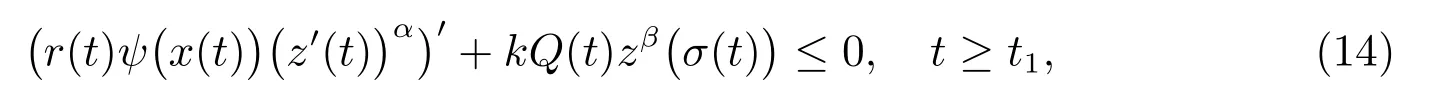
其中Q(t)=q(t)[1 ?p(σ(t))]β.定義函數
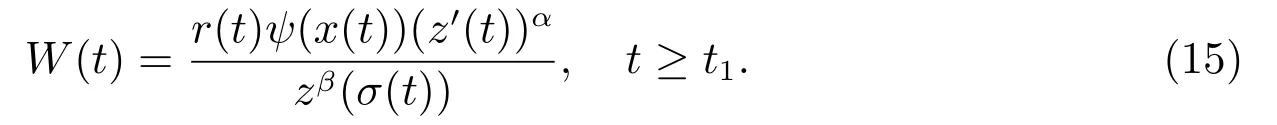
顯然W(t)>0.利用(13)–(15)式,可得
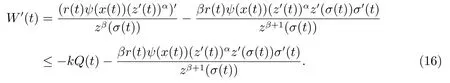
接下來,我們分兩種情況討論(16)式:
1) 當α ≤β 時,由(12)式和(16)式可得
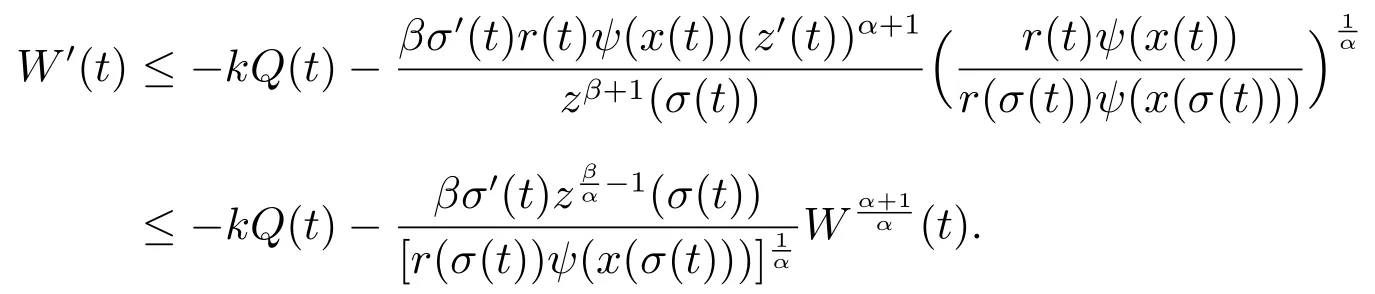
令
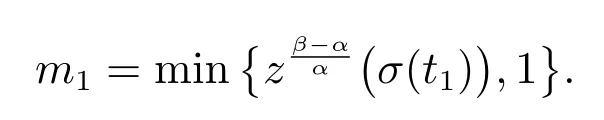
又
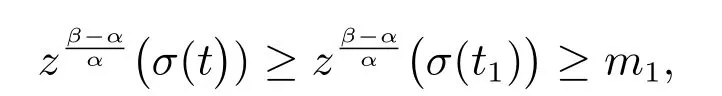
故有
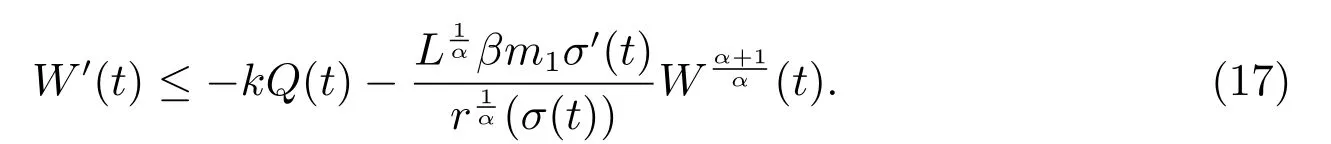
2) 當α>β 時,由(14)式得
(r(t)ψ(x(t))(z′(t))α)′≤?kQ(t)zβ(σ(t))≤0,
即
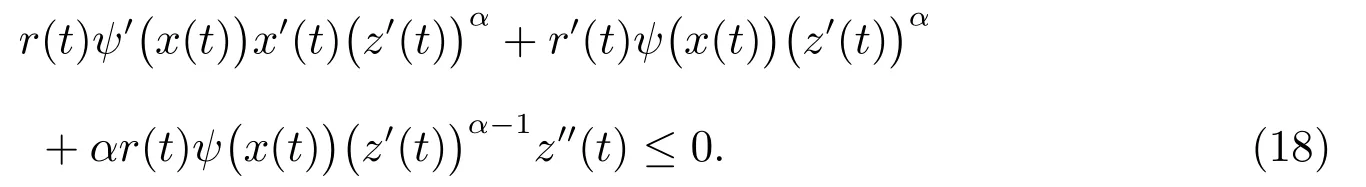
由(18)式可得z′′(t)≤0,從而有
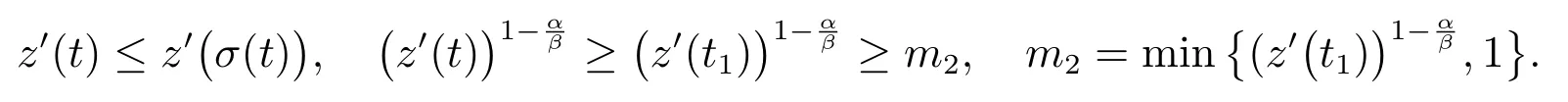
再由z′(t)≤z′(σ(t))和(16)式可得
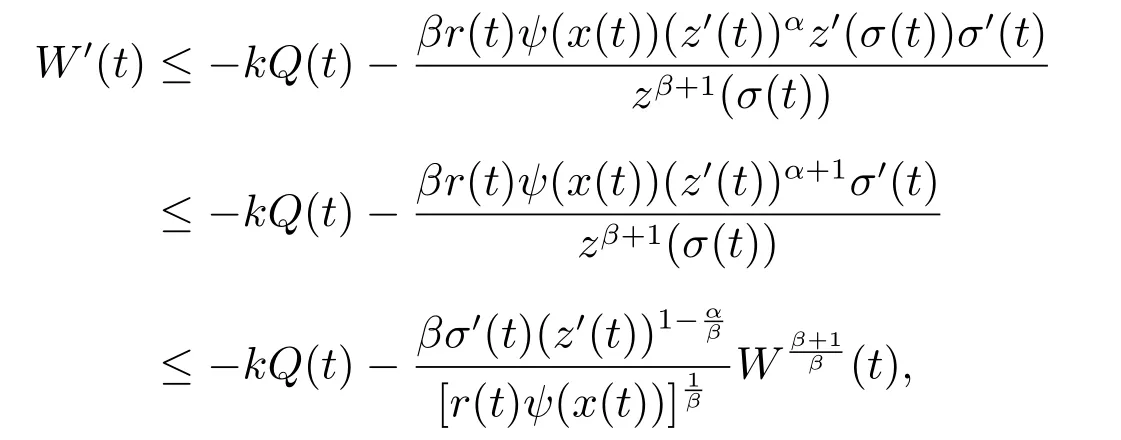
即
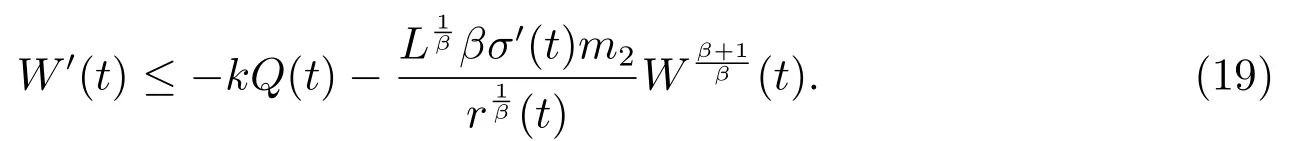
由條件(H3)知r′(t)≥0,又由(16)式知W′(t)≤0.綜上,由(17)式和(19)式,我們有
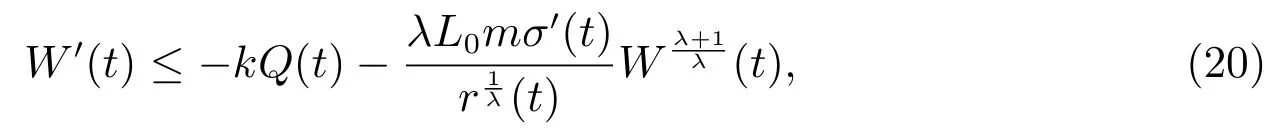
其中
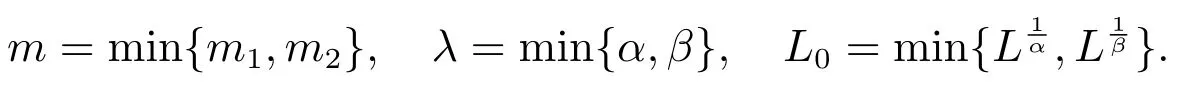
將(20)式兩端同時乘以ρ ∈C1([t0,∞),R+),并從t1到t 積分,可得
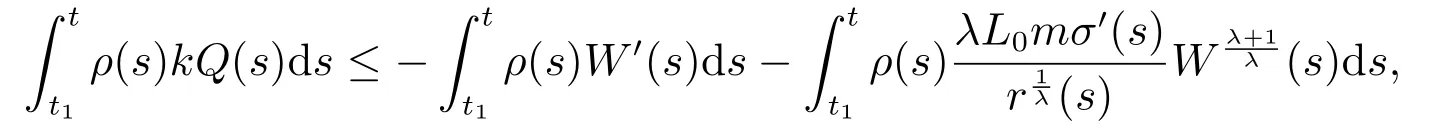
即

借助不等式
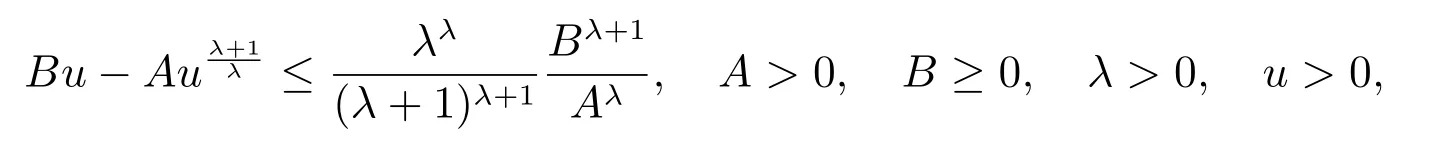
和(21)式,可得
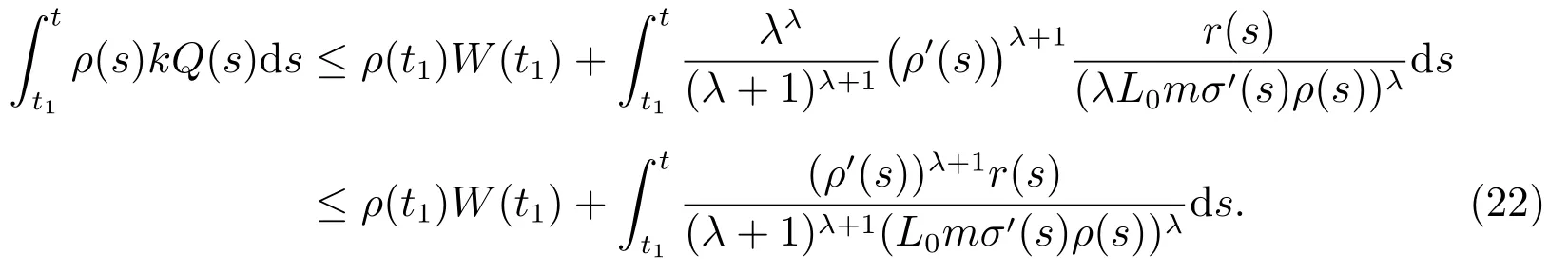
由(22)式可得
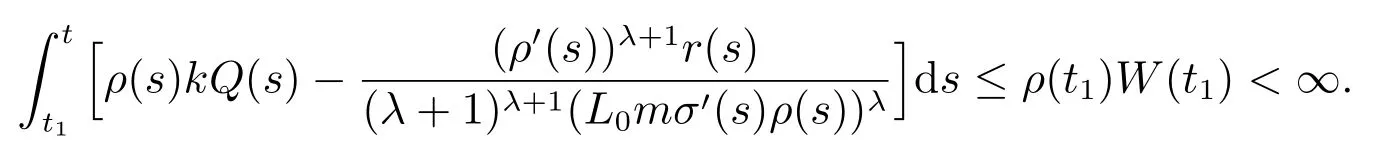
當t →∞,易知上式與條件(8)矛盾,故x 是方程(1)的振動解.
注1定理1 是將二階線性微分方程
(r(t)x′(t))′+q(t)x(t)=0
的Leighton-Wintner 振動定理推廣到擬線性中立型微分方程(1)情形,從而使前者成為定理1 的特例.另外,在本文中,若令方程(1)中的ψ(x(t)) = 1, f(x) = |x|β?1x,則方程(1)退化為文獻[3]中的方程(1).但不同的是,文獻[3]中的定理2.1 僅考慮方程(1)在α ≥β > 0 條件下的振動結果,而本文的定理1 則考慮方程(1)在α > 0, β >0 條件下的振動結果.
定理2設條件(H1)–(H5)和(7)成立,存在0 其中 證明 設x 是方程(1)的非振動解.不失一般性,設x 為[t0,∞)上的最終正解.令W(t)定義如(15)式,則由定理1 中的(20)式知 其中t1由定理1 給出.對上式從t 到∞積分,可得 令 并對上式兩邊同時除以Q1(t),可得 令 由條件(23)可知,存在常數δ >0,使得 則由(25)式,得 即 又根據不等式 可得 注2文獻[3]中的定理2 和文獻[4]中的定理3.2 都是本文定理2 的特例,文獻[3,4]分別研究了當0 < β ≤α 和0 < α ≤β 時方程的解的振動性,而本文得到了對任意α>0 和β >0 方程(1)的一切解振動的條件. 證明 設x 是方程(1)的非振動解.不失一般性,設x 為[t0,∞)上的最終正解,則z(t)最終為正.由(9)式知z′(t)最終保號且僅有兩種可能. 情況1假設z′(t)最終為正,則由定理1 的證明得出矛盾,知方程(1)在[t0,∞)上無最終正解. 情況2假設z′(t)最終為負,則存在t1≥t0,使得當t ≥t1時,有x(t)>0, x(τ(t))>0, z(t)>0 和z′(t)<0.因為 τ′(t)>0, p′(t)≥0, z′(t)=x′(t)+p′(t)x(τ(t))+p(t)x′(τ(t))τ′(t)<0, 即存在t2≥t1和正數M,使得當t ≥t2時,有xβ(σ(t)) > M.又由條件(H4)和方程(1),得 可得 定義V(t) = ?(t)r(t)ψ(x(t))(?z′(t))α,其中? ∈C1([t0,∞),R+),當t ≥t2時,顯然有V(t)≥0,且 對(28)式從t2到t 積分,可得 即 由(29)式,得 再對上式從t2到t 積分,可得 注3本文定理3 改進了文獻[6]中的定理3.1,即當ψ(x(t)) ≡1, p(t) ≡0 時,定理3 即為文獻[6]中的定理3.1.