數學概念多元表征的教學活動設計及其反思
李冬梅 劉冉
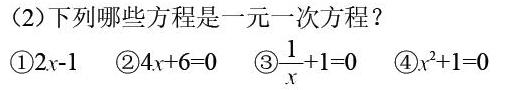
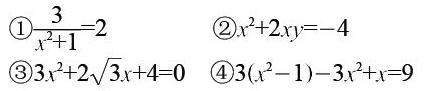
摘 要 數學概念是人們對數學關系和空間形式的抽象概括,它的特點就是概括性強、抽象度高,傳統教學活動中單一的呈現方式不利于學生深刻理解概念的本質。本文提出基于概念形成與概念同化整合的教學活動設計,這樣更利于學生對數學概念的理解,拓展思維空間,優化認知結構,提高學習的興趣。另外,在運用多元表征理論進行數學概念教學設計時應注意學生的認知負荷和學情等。
關鍵詞 多元表征 數學概念 概念形成 概念同化 認知負荷
中圖分類號:G424? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼:A? DOI:10.16400/j.cnki.kjdks.2020.05.044
Abstract Mathematical concepts refer to the abstract generalization of mathematical relations and spatial forms; It is characterized by strong generality and high degree of abstraction. The single presentation mode of teaching activities in the design does not make use of students deep understanding the essence of concepts. This paper puts forward the teaching activity design of the integration of concept formation and concept assimilation. It can promote students understanding the mathematical concepts, enhance the interest of learning, expand thinking space and optimize the cognitive structure. We should pay attention to students' cognitive load and learning conditions when we use the multi-representations to design teaching activities of mathematical concepts.
Keywords multi-representations; mathematics conception; conception form; conception assimilation; cognitive load
數學概念是人們對數學關系和空間形式的抽象概括,是建立數學公理、法則的基礎,也是進行數學運算、推理、判斷和證明的重要依據,更是展現數學思維、進行數學交流的重要工具。它具有高度的概括性和抽象性和一定的系統結構。[1]正是由于數學概念的這三個特點,造成教學中學生難以高效、準確理解與運用。
多元表征起初是由英國數學家迪因斯在上世紀60年代提出的多元具體化原則,該原則是指為了讓學生建立抽象的數學結構,而呈現給學生具體的實物模型或者創設恰當的情境。數學概念的多元表征指通過運用多種表現形式表征數學概念,反映概念的本質含義,促進學生掌握概念的結構,內化概念的認知圖式。它在教學中的作用主要表現在促進學生數學概念的理解,提升學習的趣味性;拓展學生的思維,促進積極認知投入;豐富學生的知識,優化其認知結構。
1 運用多元表征進行數學概念教學活動設計的過程
數學概念教學的本質就是教師通過實施有效的教學活動,促使學生能夠概括出數學對象的共同本質屬性,形成概念表象,理解數學概念的內涵與外延,建構良好的概念圖式。教學活動設計在其中起到重要作用。通常學生理解概念主要是概念形成和概念同化兩種方式,[2]在教學活動設計中,除了基于概念形成、概念同化的教學活動設計外,最重要的是基于概念形成與同化整合的教學活動設計。
基于概念形成與概念同化整合的多元表征教學設計,即綜合考慮概念形成和概念同化的特點,并結合相關數學概念的特點,合理設計教學活動。其教學活動設計的過程:(1)復習舊知;(2)呈現新知的具體實例;(3)抽象概念實例的共同屬性;(4)建立新舊知識的聯系,深化理解;(5)運用概念。特別是在呈現新知的具體實例、抽象概括共同屬性和建立新舊知識的聯系三個環節中,教師要巧用多元表征,注重學生原有知識基礎,觀察分析概括概念的本質屬性,建構新的認知圖式。下面我們以一元二次方程的概念教學為例,說明如何進行概念形成與概念同化整合的多元表征教學活動設計。
1.1 復習舊知識
(1)以前我們學習過一元一次方程,請同學們寫出一個一元一次方程,說出它的一般形式( ?a≠0),并從中概括出一元一次方程的特點。
(2)下列哪些方程是一元一次方程?
在復習舊課環節,教師設計兩個題目,題目1通過舉例,讓學生回憶一元一次方程的形式,并概括出它的一般形式,學生的思維經歷了特殊到一般的形式,能夠快速撲捉到一元一次方程的特點,快速推出它的一般形式。題目2是運用一元一次方程的概念進行判斷,即能夠運用概念做簡單的分析判斷。復習舊知識,這部分設計,主要的是為學習一元一次方程的概念建立聯系、搭建支架,為同化新概念做鋪墊。在教學活動設計的表征形式上,教師也運用情境表征、語言表征、模型表征等多種形式。
1.2 探索新知識
1.2.1 呈現問題
列出下面各題的數量關系式,并說說它們有什么特點?
(1)正方形桌面的面積是2m2,設正方形桌面的邊長是xm,則邊長與面積之間的數量關系怎么用方程表示?
(2)矩形花圃一面靠墻,另外三面所圍的柵欄的總長度是19m,花圃的面積是24m2,設花圃的寬是xm,花圃的長是(19-2)m,則花圃的寬與面積之間的數量關系怎么用方程表示?
(3)長5m的梯子斜靠在墻上,梯子的底端到墻面的距離比梯子的頂端到地面的距離多1m,設梯子的底端到墻面的距離是xm,怎么用方程描述其中的數量關系?
1.2.2 獨立思考
老師先讓學生思考5分鐘,獨立嘗試求解。
1.2.3 討論分析
教師組織學生分小組交流合作討論,建立同桌,前后位之間4人一個小組,就問題展開小組討論,分析問題的思考過程,解答流程。教師可以依次與每個小組交流,查看學生的學習情況,針對學生的問題,并作必要的引導。
1.2.4 小組匯報
根據學生小組合作學習的情況,教師請各小組代表分別分享各自的答案,并就每個問題講述下思考過程,教師并做引導與點評。
1.2.5 歸納總結
針對學生求解的方程,,,,引導學生化簡方程,小組合作交流,看看這些方程有哪些特點?由學生總結出一元二次方程的含義,特點,教師做最后的重點說明,并就一元二次方程的一般式(a、b、c是常數,a≠0)中各部分的名稱與系數做重點講述。
1.3 鞏固練習
當堂練習1:下列方程中哪些是一元二次方程?
當堂練習2:將方程化成一元二次方程的一般形式,并寫出其中的二次項系數、一次項系數和常數項。
在探索新知識環節,教師設計三個具體的問題情境,通過組織學生思考,討論,列出每道題的方程,然后觀察、分析、討論交流,歸納出一元二次方程的概念和特點,理解一元二次方程的一般形式,建構一元二次方程的認知圖式。在整個教學設計中,通過小組合作學習,學生經歷“獨立思考—討論分析—小組匯報—歸納總結”這一學習過程,培養自身數學抽象能力、數學建模能力和合作交流能力。
在鞏固練習環節,教師設計兩個題目,練習1是關于一元二次方程概念的判定,練習2是關于一元二次方程各個項與系數的掌握情況,通過上面的教學活動設計,這兩個教學目標很自然的就能達到。在多元表征方法的運用上,兩個教學環節中,教師采用了情境表征、語言表征、符號表征和模型表征等相結合,引發學生的認知思考,交流討論,在小組合作交流中,更好地理解一元二次方程的概念,最終內化認知圖式。此外,通過該教學設計,也反映出教學設計者背后的教學理念。在知識觀上,反映出知識的獲得是由學生基于原有的知識經驗主動建構形成的。在學生觀上,摒棄了傳統教學中的直接灌輸,反映出知識的學習并不簡單由外到內的轉移和傳遞,而是學生通過原有的知識經驗同化新知識,豐富和改造自身知識經驗。在教學觀上,教學就是要激發學生原有的相關知識經驗,促進學生知識經驗的“生長”,教師的角色是一個引導者、促進者。
2 運用多元表征進行數學概念教學活動設計的反思
通過對以上教學活動設計的分析,我們自然有這樣的疑問,運用多元表征法進行數學概念的教學活動設計時,我們需要注意什么問題?是否表征形式越多越好呢?我們覺得應從以下兩個方面考慮:
(1)有效的教學活動設計取決于認知負荷。認知負荷理論是由Sweller等人證實并發展來的理論,認知負荷指工作記憶系統針對某一具體的學習任務進行加工和保持信息過程中所承受的負荷總量,它包括外在認知負荷、內在認知負荷、有效認知負荷。外在認知負荷指由于教師教學內容選擇不當,教學內容組織呈現方式不當導致與認知加工過程無關的活動。[3]它指向教師所選擇的教學內容與教學內容的呈現方式是否恰當。內在認知負荷指所學的內容材料本身所含有信息的數量以及各信息之間相互作用而對認知加工活動所產生的消極影響。它在一定程度上反映了學習任務的復雜性和難易度,學習任務越復雜,其產生的內在負荷就愈大。有效認知負荷指學生針對學習任務進行認知加工處理,建構認知圖式的過程中產生的認知負荷,它指向于學生自身學習的過程。根據認知負荷理論,學生學習過程中產生的外在認知負荷、內在認知負荷與有效負荷三者負荷的總和應控制在學生負荷總量的最近發展區之內,有效的教學活動設計遵循的原則應該是降低外在負荷,內在負荷,增加有效負荷,引導以促進學生建構恰當的認知圖式。
(2)有效的教學活動設計充分考慮學生的學情。既然認知負荷理論決定了教學活動的設計,所以依據認知負荷理論的基本觀點,教師有效的教學活動設計必須充分考慮學生的學情。比如說學生的原有知識基礎,數學邏輯思維水平和學習方式等等。只有充分考慮學生的學情,根據不同的學生學情,精選學習內容,優化教學內容的呈現方式,才能將外在認知負荷、內在認知負荷與有效負荷降到學生所成承受的最近發展區之內。
基金:湖南省2019年普通高校教學改革研究項目(2019-291-477)
參考文獻
[1] 曹一鳴,張生春.數學教學論[M].北京:北京師范大學出版社,2010:144-145.
[2] 何小亞,姚靜.中學數學教學設計[M].北京:科學出版社,2012:42.
[3] 唐劍嵐,周瑩.認知負荷理論及其研究的進展與思考[J].廣西師范大學學報哲學社會科學版,2008(2):76.

